双波段比色测温技术的应用
2019-05-09张林张志杰李岩峰
张林,张志杰,2,李岩峰
(1.中北大学 仪器与电子学院,山西 太原 030051;2.中北大学 仪器科学与动态测试教育部重点实验室,山西 太原 030051)
非接触测温中的辐射测温具有响应速度快、测量温度高以及不影响温度场等优势,因此它得到了快速的发展,并广泛应用于诸多领域。其中,双波段比色测温法已在高温场测量中取得了许多的成就,开发了许多不同类型的测温仪,例如基于DSP的比色光纤高温测温仪[1],基于彩色CCD的高温辐射测量仪[2],智能便携式镁合金燃点比色测温仪[3]等。但是在低于1 000℃的中低温场的相关研究比较少。本文介绍双波段比色测温的原理,研究温度测量时双波段的选取问题,以及实际系统中标定方法的选择、误差的分析等。
1 比色测温原理及双波长的确定
1.1 双波段比色测温原理
辐射测温的基本原理是基于黑体辐射的普朗克定律。普朗克曲线如图1所示。普朗克定律描述的是辐射能量的光谱分布,它的相应公式表明了光谱黑体辐射出射度与波长和绝对温度的关系:

式中:c1=2πhc2=3.74×10-16;c2=hck=1.43879×10-2,c为光速,k和h分别为玻尔兹曼常数和普朗克常数[4]。
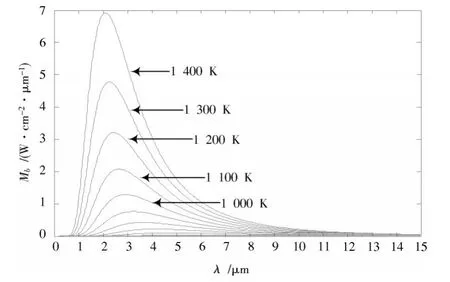
图1 普朗克曲线Fig.1 Planck curves
根据普朗克定律可以得到很多种辐射测温方法,包括单色辐射式测温法、全辐射式测温法和比色式测温法等[5]。双波段比色测温的原理是根据被测温度场在两个波段上的光谱辐射出射度的比值与温度的关系来测量温度的。在实际应用中,比色测温仪是利用不同工作波长的两路输出信号比值与温度单值函数来确定物体温度的。当选择合适的波长后,发射率的影响可以忽略不计,这样就可以大大减少发射率带来的误差,这也是比色测温法最主要的优点[6]。
1.2 双波长的确定
1.2.1 双波段的选取范围
比色测温的核心是双波长的选取。影响波长选择的因素很多,包括发射率、测温范围、大气吸收等。其中发射率的确定很困难,因此选择两个相近的波长,使得热源在两个波段的发射率尽量相近,降低发射率对测温误差的影响[7]。实验的测温范围为100~1 000℃(373~1 273 K)。温度越低,总的辐射功率越小,相应的探测波段辐射功率也小,探测器不容易检测到信号。探测波段越小的位置辐射功率也越小[8-9]。根据维恩位移定律,计算出测温段的峰值波长为2.28~7.77 m。
由于大气环境含有水汽、二氧化碳和臭氧,这些物质会吸收辐射能量导致无法测量或者测量不精确,因此要根据大气吸收光谱选择合适的波长。水汽分子是红外辐射的主要吸收体,较强的水汽吸收带位于0.71~0.735 m,0.81~0.84 m,0.89~0.99 m,1.07~1.20 m,1.3~1.5 m,1.7~2.0 m,2.4~3.3 m等。为了提高信噪比,所选波长应该接近峰值波长,并根据探测器的响应范围等相关因素,应选择1.5~1.7 m波段进行比色测温。
1.2.2 中心波长的选取
输出信号的比值与温度有着很复杂的数学关系。选择合适的测温参数,对提升测温精度很重要,中心波长λ1={1.5,1.55,1.6,1.65,1.7}μm,λ2={1.55,1.6,1.65,1.75}μm,两个所选波长的带宽都为0.04 m,对应的两个波长辐射功率之比R与温度T关系的曲线,见图2。由图2可以看出,在所测的373~1 273 K之间,波长越小,辐射功率之比变化范围越大,分辨率越好[10-12]。

图2 波长与辐射功率之比的关系Fig.2 Relationship between wavelength and radiant power ratio
从灵敏度来判断,定义灵敏度S为温度变化1 K时R的变化量[13],即S=ΔRΔT。由图 3可知,波长越小,对应的灵敏度越高。
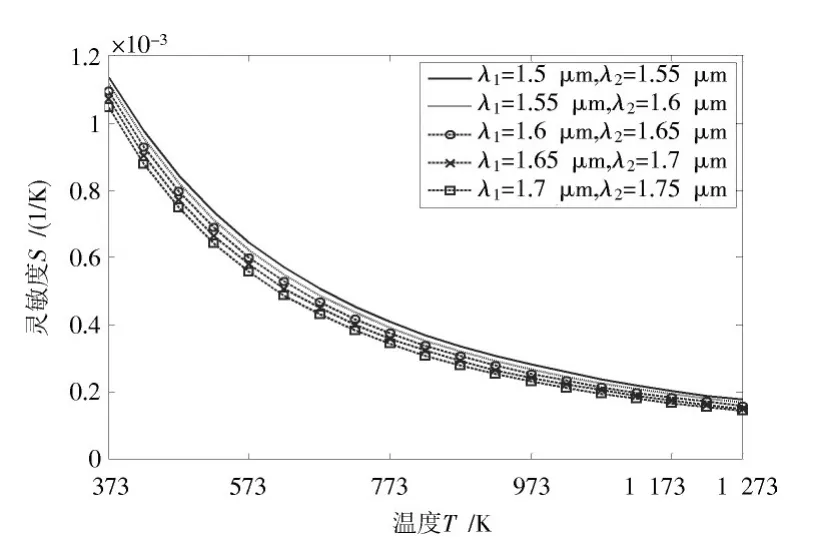
图3 波长与灵敏度的关系Fig.3 Relationship between wavelength and sensitivity
当两波段的中心间距从0.05 m减少为0.04 m时,两个所选带宽仍为0.04 m。对比图2~图4中曲线的Y轴变化范围,可知此时的辐射功率动态变化范围将减小,而且灵敏度也降低;但波长越近,发射率的影响越小,测温越准确,考虑到发射率是测量准确性的主要影响因素,并根据实际滤光片的情况,选用两块较近波长的滤光片即可。
由于实际滤波片的带宽基本已定,而且增加带宽的目的是提高信噪比,缩小带宽却可以提高精确度。一般来说,带宽的最大宽度由探测元件限制,带宽的最低限度由信噪比决定。
考虑改变带宽的影响,选择中心波长λ1={ 1.5,1.6,1.7 }μm,λ2={ 1.55,1.65,1.75 }μm时,两个波段的带宽分别为0.02 m,0.04 m,0.06 m。由图5可知,带宽的改变基本不影响波长辐射功率之比。

图4 两波长间距减小后的曲线图Fig.4 Curve diagrams after spacing between two wavelengths was reduced

图5 不同带宽的曲线Fig.5 Curves at different bandwidths
由以上分析可以得出,带宽的改变并不影响结果;波长越小,辐射功率变化范围越大;分辨率越高,灵敏度越高。
因此,在选择两波长时,应在可探测辐射强度和大气窗口所限定的波段内,让两波长尽量小,间距尽量接近。本实验选择的滤光片波长分别为60~1 550 nm和60~1 600 nm。
2 比色测温系统
比色测温系统由光学探头、分束光纤、滤光片和铟镓砷光电探测器等组成。其中,铟镓砷光电探测器具有放大作用,响应波长为0.8~1.7 m。系统的组成框图见图6,部分实验设备见图7。
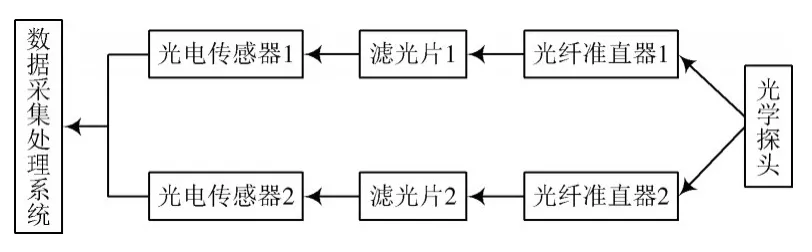
图6 比色测温系统框图Fig.6 Block diagram of colorimetric temperature measurement system

图7 部分实验设备Fig.7 Partial experimental equipments
本系统是由光学部分和电学部分共同组成的。辐射光源发出的辐射光由光学探头接收,通过分束光纤平均分为两路光信号;然后经过光纤准直器和滤光片,被铟镓砷光电探测器所接收、放大;最后通过数据采集处理系统进行信号的采集和处理,显示出电压信号。
3 黑体炉标定实验
在测试系统中,光的辐射能量转化为电压信号。测温系统在两个波段处的输出电压之比与双波段辐射亮度之比间的函数关系为:

式中:f(λ)为滤光片光谱透过率;D(λ)为光电转换器的光谱响应函数;F(λ)为光学系统的光谱透过率;ε(λ,T)为所测物体在某一温度和波长处的发射率;其中令:

则可以简化为:

当两波段接近,且带宽较窄时,两波段平均发射率相等,可以认为K是一个与波长无关的比例系数,这是K值法。
由式(2)可知,通过比色测温系统得到的两个输出端的电压值可以求出此刻物体的温度。在基于黑体炉的标定实验中,根据所测电压的比值和此刻黑体炉的温度,实验选取两种方法对比色测温系统进行标定,并对两种方法进行比较。一种是K值法,根据式(3),当测温距离确定后,K值应该是一个由系统参数确定的常量,实测中可由式(1)与式(2)反解得到当前温度;另一种是曲线拟合法,拟合一条电压比值和对应黑体炉温度的曲线并确定曲线的方程,实测中将测量结果的比值代入方程即可求得对应的温度。
3.1 两种标定方法的对比
在实验系统的测试中发现,400℃以下由于辐射强度等原因会测不到,400~600℃由于辐射产生的电压变化相对于噪声干扰带来的变化并不明显,误差较大。因此本实验主要以600℃以上测量为准。
本实验中光学探头与黑体炉的距离为10 cm。实验一所测的温度为600~940℃(间隔20℃),实验二所测的温度为610~950℃(间隔20℃)。为了减小测量误差,实验中每个温度点均进行3次测量,取3次电压的平均值作为实验结果。
使用K值法对实验一结果进行求解,得到的K值为0.798 9;使用曲线拟合法对实验一结果进行二次拟合,结果方程为:
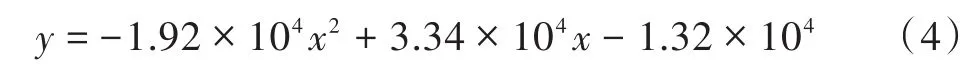
式中:x为电压比值;y为温度。
方程对应的曲线如图8所示。
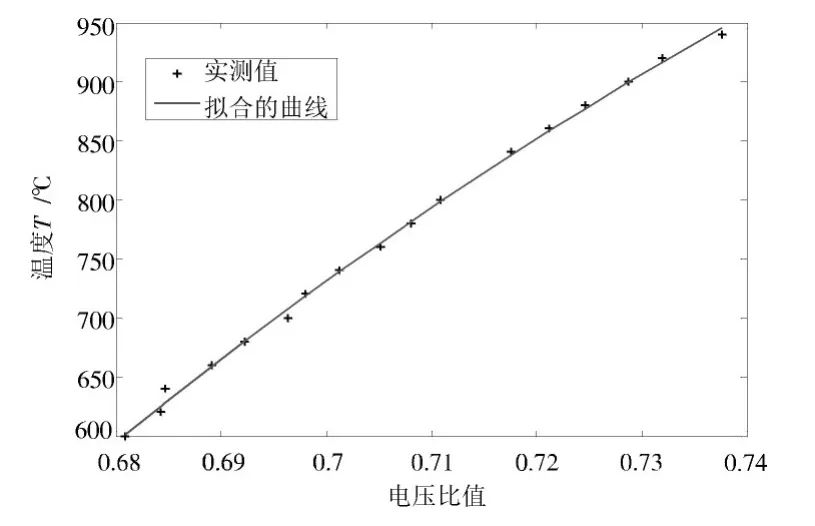
图8 曲线拟合法结果图Fig.8 Result diagram of curve-fitting method
分别用两种方法对实验二结果进行误差分析,结果见表1。由图8和表1可知,曲线拟合法效果更好,系统测温的稳定性更好。

表1 两种方法的对比Table 1 Comparison of two methods
3.2 测温距离对测量误差的影响
实验中探测器与热源的距离长短会影响到K值。从理论上来说,距离越远,大气干扰性越大;距离越远,周围环境的影响越大;距离越远,所接收到热辐射强度会迅速降低。因此,距离越远,测量误差越大。
调节探测器的旋钮,使得再次进行的重复性实验的测温距离拉长到16 cm,其他条件不变。实验三所测的温度为600~940℃(间隔20℃),实验四所测的温度为610~950℃(间隔20℃);实验中每个温度仍均测3次,取其平均值作为测量结果。
实验三所测到的平均K值为0.715 9,实验四所测到的平均K值为0.722 4。对比实验一与实验三、实验四的K值结果可以得出结论,测温距离很明显影响到K值,对于不同的测温距离,应使用不同的K值或者拟合方程。
综合实验一至实验四的结果,根据测温距离不同进行对比。温度范围为600~950℃(间隔10℃),测温距离分别为10 cm和16 cm。结果如图9所示,易知测温距离越大,误差越大。
由黑体炉标定实验可以得出结论:在安全距离内,距离热源越近误差越小;在中低温段,拟合曲线法比K值法误差更小;由于环境、能量等方面的影响,对于不同的测温距离,测温系统应使用不同的K值或者拟合曲线。
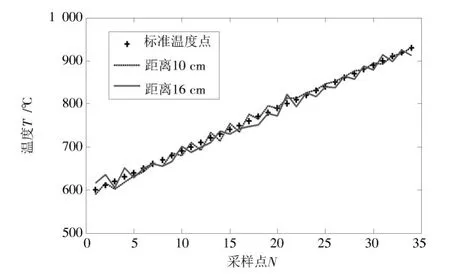
图9 不同测温距离对比图Fig.9 Comparison of different temperature measurement distances
4 结论
本文详细介绍了双波长的选取原则,应考虑大气环境等因素选择合适的波段,在可探测强度的前提下选择更小的波长,让两波长尽量接近。在实际系统的标定中,拟合曲线法比K值法更适合。温度较低时测温距离对测量精度影响很大。由于低温辐射强度低、系统噪声等原因,一般会出现辐射强度过低无法测量、干扰因素导致误差太大等现象。
