巧设驱动性问题点燃思维的火花

王令壮

【摘要】问题是数学学习的灵魂，是点燃思维火花的导火索，是贯穿一堂课的主要脉络.一节优秀的教学设计，必有高质量的驱动性问题作为支撑.看似简单的知识，通过巧设问题，引起学生的深度思考，促进学生深度学习，真正使学生从根本上理解知识，形成知识体系.

【关键词】教学设计;一次函数图像;知识体系

问题驱动教学法是基于问题的教学方法，是一种以学生为主体、以专业领域内的各种问题为学习起点，以问题为核心规划学习内容，让学生围绕问题寻求解决方案的一种学习方法.教师在此过程中的角色是问题的提出者、课程的设计者以及结果的评估者.

巧设驱动问题能够提高学生学习的主动性，提高学生在教学过程中的参与程度，容易激起学生的求知欲，活跃其思维.下面我结合鲁教版数学七年级上册，学生初次学习一次函数图像的作法时例题的讲解，谈一下如何巧设驱动型问题，引导学生有条理的思考，理解知识.

一、例题讲解

例题作一次函数y=x+2的函数图像.

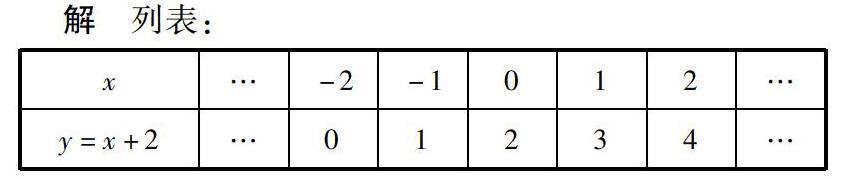
解列表：

x…-2-1012…

y=x+2…01234…

描点：

連线：

教师提问1：自主学习教材函数图像概念以及画图像例题，思考：函数的图像概念是什么？作函数图像分哪几步？学生1答：把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标，在直角坐标系中描出它的对应点，所有这些点组成的图形叫做该函数的图像.作图分三步：列表、描点、连线.

教师提问2：所列表格中x的值是如何得到的，y的值是如何得到的？学生2答：x的值是任意取的，y的值是通过x代入关系式计算得到的.

教师提问3：关系式y=x+2中的自变量x可以取哪些数？学生3答：可以取任意数，有无数种取x的方法.

教师提问4：回答得很好，由于我们不可能把所有数取到，所以只能选取其中的几个点来代表，那么你打算如何选取这几个点？学生4答：选择方便计算和表示的点.

教师提问5：表格中的省略号代表什么意思？学生5答：x和y可以取无数个点，可以无限大，无限小.

教师提问6：你能从表格中找到我们都取了哪些点？坐标分别是什么？如何确定？学生6答：共取了五个点，坐标分别为：（-2，0）（-1，1）（0，2）（1，3）（2，4），x的值为横坐标，相应y的值为纵坐标.

教师提问7：描点之前，要先做什么？学生7答：建立直角坐标系.

教师提问8：建立直角坐标系有哪些注意问题？学生8答：要规范的画坐标系，用铅笔直尺画，注意标注坐标轴、原点、单位长度以及正方向.

教师提问9：你能在坐标系中找到点（-2，-3）吗？学生9：到黑板示范找点的过程.教师重点强调找的时候要注意对应关系.

教师提问10：“依次连接”是什么意思？学生10答：按照顺序连接.

教师提问11：你能上台示范一下吗？（学生一般初次上台连接，通常会出现不规范的地方）

教师提问12：他画的对吗？有没有不规范的地方？学生12答：连线时，两端要“出头”.

教师提问13：为什么连的时候，两端要“出头”？学生13答：“出头”代表无限延长，x、y可以取任意数，体现在图像中就是要“出头”.

教师提问14：取点的时候，通常我们取五个点，可不可以取更多的点？

学生14答：可以，取的点越多，图像越精确.

二、在问题处理时，学生未必按照预设的答案回答，教师需要灵活处理

1.在画图时，可能会得出一次函数的图像是一条直线的结论，学生只是直观感受，教师可引导学生后面加以验证.

2.学生可能未描出所有的点，就着急连线，需要教师加以提示，要把所取点都描出再连.

三、这样设置问题，有以下作用

1.每个环节都设置了很多的问题串，就像一个个台阶一样，层层递进，把难度降低，把问题细化，学生更容易理解接受.

2.问题串的设置使讲解的过程变成了师生互动的过程，课堂气氛更活跃、更能调动学生的积极性，比直接灌输效果要好.

3.问题串的设置，有利于促使学生深度学习，培养学生的数学思维.

当然，问题的设置，对教师的备课提出了更高的要求.要想设计出高质量的问题，教师必须在了解学情的基础上，深度备课，充分预设才行，应该说，对提高教师的专业发展，很有帮助.

【参考文献】

[1]孙绍荣.高等教育方法概论（修订版）[M].上海：华东师范大学出版社，2010.