基于电感式磁传感器的车位检测算法设计

2019-05-08刘守印

传感技术学报 2019年4期

李凤,董胜,刘守印

(华中师范大学物理科学与技术学院,武汉 430079)

随着我国私家车保有量日益增加,交通设施受到前所未有的压力,根据公安部公布的数据,截至2018年底,全国机动车保有量达3.25亿辆,与2017年底相比增加1556万辆,其中汽车保佑量超过2亿辆[1]。国家发改委公布的数据显示,目前我国大城市小汽车与停车位的比例约为1:0.8,中小城市约为1∶0.5,而发达国家约为1∶1.3,保守估计我国停车位缺口超过5 000万个[2]。

由于停车场的车位数量远远不及车辆数量,“停车难”已经成为了一个社会性问题。居民出行时间极大部分浪费在寻找停车位上,由此造成的尾气污染、噪声污染相当严重。同时,在医院、居民小区、火车站等车流密集地区,由于寻找停车位带来的交通拥堵情况也十分严重[3]。因此,及时获取停车位占用情况,帮助居民获取附近空余停车位非常重要。

由于近年来传感器网络的飞速发展,各种传感器和感知技术被应用在车辆检测上,其中包括视频技术[4]、感应线圈、超声传感器、红外传感器以及磁传感器[5-6]。其中磁传感器因其低成本、高精度、小体积等优势,近年来广受业内学者的青睐[7]。

根据磁传感器的测量原理可以分类为霍尔元件、磁通门传感器、磁阻传感器和电感式传感器[8]。霍尔元件和磁通门传感器虽然分辨率高,但是体积过大,并不适合用于车辆检测。磁阻传感器易被磁性物质磁化,导致基线漂移,消除漂移的方法会增加额外复杂度,因此本文选择PNI公司的精密电感式磁传感器RM3001,三轴传感器配合PNI12927驱动芯片进行磁场测量,其输出为数字量,直接送入单片机进行处理计算,不需要进行信号放大和A/D转换。该测量方法省去了大量硬件电路,并且具有精度高、体积小、成本低、稳定性好的优点[9]。

本文基于PNI12927驱动三轴电感式磁传感器,设计一种基于隐马尔可夫模型HMM(Hidden Markov Model)的车辆检测算法。使用MSP430低功耗单片机对传感器采集的磁场数据进行计算,得出车辆检测结果,获取车位占用情况,通过LoRa将检测结果传输至服务器,用户通过客户端软件实时查看停车场空车位分布情况,系统框架如图1所示。检测装置体积小,便于安装,功耗低,寿命长,且经过长时间实践验证,算法检测准确率为98.11%。

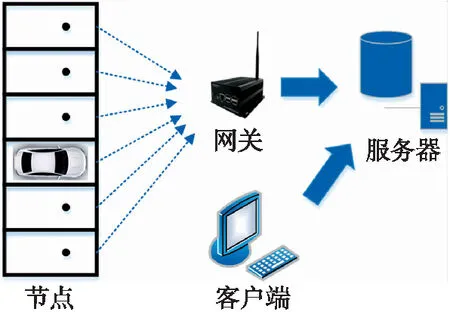
图1 系统框架图

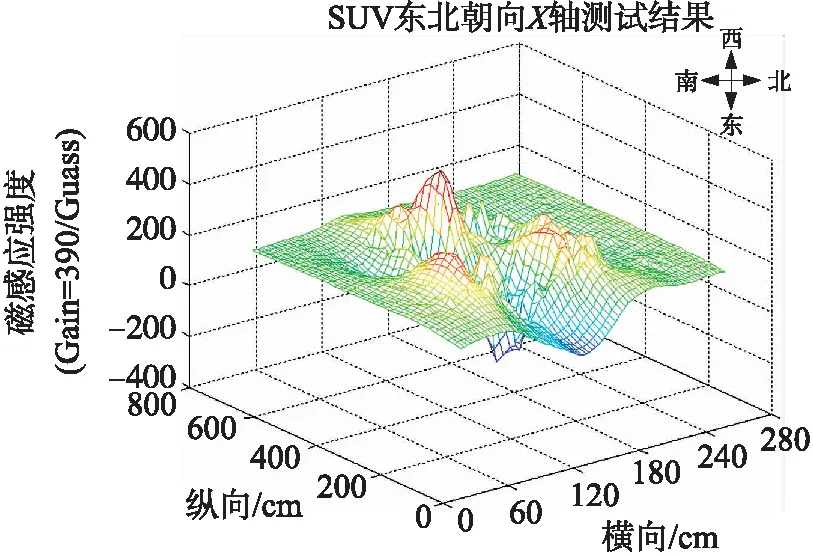
图2 部分车辆磁场分布实验结果

1 研究基础与本文工作

在进行车辆检测算法设计之前,本文作者结合磁阻式传感器HMC5983和ZigBee无线传输方式,进行了乘用车底部地磁场分布特性的实验研究。实验中每隔10 cm取一个点进行磁场测量,最终绘制三维图,直观体现乘用车底部地磁场分布情况,详细实验结果在文献[10]中,于2016年12月公开发表,其中部分实验结果如图2所示。从实验结果中,我们可以发现:①车辆对地磁场产生的扰动具有边界性。乘用车对车辆四周30 cm以外的区域扰动较小,在车辆底部磁场扰动非常明显,车辆外围扰动急剧减小,由此可见通过磁场检测判断车辆存在与否的方案是可行的。②车辆停放方向与车辆对磁场扰动分布相关性较小。当车辆停放方向分别为南北、东西等方向时,乘用车对从停车位上的磁场扰动并不会随方向变化而产生较大变化,这说明根据磁场判断车辆存在与否的结果与停车位的朝向无关。③在车辆底部不同部位,磁场的扰动存在较大范围差异。由于车辆材料分布不均,例如乘用车车头发动机部分、车轮、车轴金属材料部分,对磁场的扰动明显与车辆中部座椅部分不同。因此,车辆和检测节点的相对位置变化,对检测结果具有明显影响。实际应用中,我们需要将节点安装在车位靠近车头或车尾1/3处(即偏移车位中点1/3处),尽量减小检测节点与车辆的相对位置变化带来的误差。

在现有研究基础上,本文的研究工作主要包括以下几点:①基于电感式磁传感器设计了地磁车位检测节点硬件电路,使用LoRa无线传输技术,将测试结果上传至网关,再经由网关传输至服务器存储,以供测试查看。②将停车位状态转换抽象为一种隐马尔可夫模型,从检测节点角度出发,建立了便于算法设计的车位状态转换模型。③利用HMM的特点,设计了一种基于HMM的车辆检测算法,并验证了算法可行性,通过长时间实际应用测试了算法检测准确率。④建立了车位无车基线更新、稳定状态更正等机制,增加检测算法的鲁棒性和准确性。

2 硬件设计

车位检测节点硬件部分主要采用了PNI12927驱动三轴电感式磁传感器,测量范围为-1 100 μT至1 100 μT,空闲模式电流低至1 μA,工作温度为 -40 ℃～85 ℃,能够在冬夏时节露天停车场的温度环境中保持正常工作。

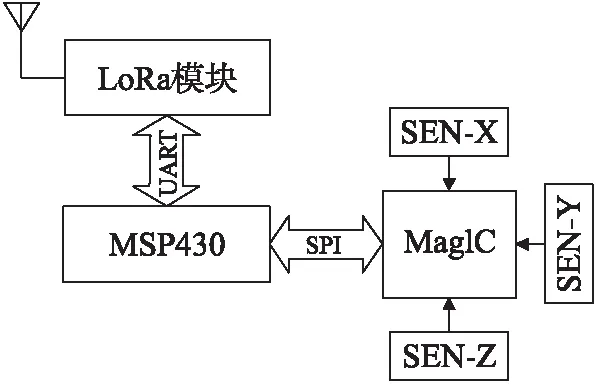
图3 检测节点硬件设计框图

将PNI12927(即MagIC)和3个单轴电感式磁传感器作为磁传感器整体,通过SPI接口与低功耗单片机MSP430相连,单片机计算结果通过串口送至LoRa模块,以无线的方式上传至网关。检测节点硬件设计框图如图3所示。

图3中,P NI12927和MSP430之间使用SPI接口进行通信。由于PNI12927和三轴电感式磁传感器的输出是数字式的,不需要AD转换和滤波电路,所以SPI接口可以满足需求。LoRa模块和MSP430之间使用串口通信,主要用于MSP430向LoRa模块传输计算结果和由MSP430定时上传的心跳信息(其中包括当前车位状态和磁场测量值等内容),同时,用户通过无线传输下发指令至LoRa模块,再经由串口送至MSP430进行指令响应操作,其中指令包括初始化指令、心跳周期更改指令等。

节点采用一次性锂亚电池ER34615M供电,电池供电电压3.6 V,经过MCP33转为3.3 V为传感器供电,电池容量为13 000 mAh。经测试,节点发送电流为48 mA,接收电流为12 mA,磁场采集电流为3.5 mA,休眠电流为3.6 μA,经计算,在正常运行的停车场中,采用2 min/次的心跳发送频率,节点使用寿命为3.8年。

电池尺寸为33 mm(直径)×61.5 mm(高),节点电路板为40 mm×51 mm,整个节点外壳尺寸为100 mm(直径)×95 mm(高)。因此只需要在车位地面钻一个直径为10 cm深度为10 cm的孔即可安装,采用水泥或灌封胶固定节点,并且可以将节点内胆取出,进行电池更换或电路检修工作。因此节点的硬件及实物设计具有寿命长、易安装、易维护的优点。

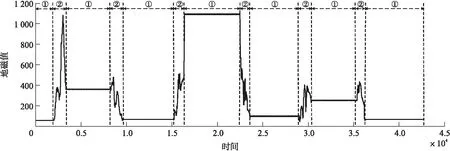
图6 车辆停入、驶出车位的波形和状态

3 车位检测算法设计

3.1 车位状态模型化

马尔可夫模型是基于马尔可夫链提取的系统模型,马尔可夫链的含义是已知系统的现在,那么系统的将来与过去无关[11],即马尔可夫模型具有离散性、随机性和无后效性[12]。通常意义上我们理解为马尔可夫模型中,每一个状态只与系统前一个状态有关。在停车事件中,我们将停车位状态分为车来、有车、车走、无车4个状态,每一个状态只与前一个状态有关,符合马尔可夫模型的概念。

HMM具有马尔可夫链的无记忆特性,即每一个状态只跟前一个状态有关,同时具有隐藏性[13],即每一个状态都含有隐藏状态。隐马尔可夫模型的状态转换如图4所示。其中ωi为隐藏状态,vi为可见状态,aij为转换概率。通常我们是通过对可见状态vi的规律研究,推断隐藏状态ωi。

图4 HMM状态转换图

在车位检测系统中,从检测节点的角度出发,只能获得磁场的波动和稳定两种状态,波动状态即地磁场被扰动时产生剧烈波动的情况,稳定状态即车位上地磁场没有较大变化的情况。而车辆是否停入车位,在检测节点角度观察属于隐藏状态,需要通过算法判定。

本文将停车位状态变化抽象为HMM模型,状态转换如图5所示。

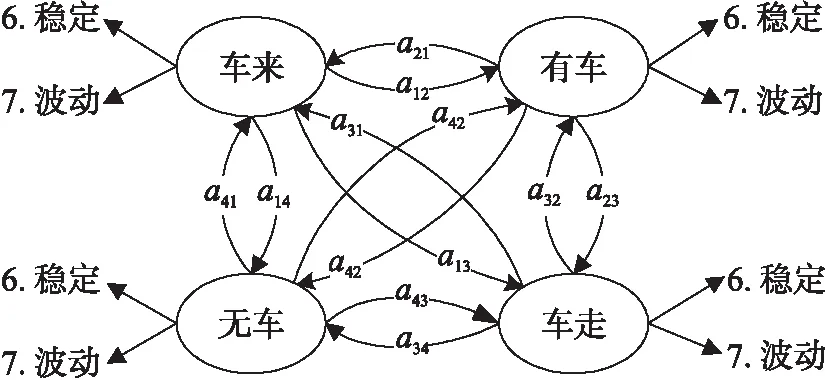
图5 停车位HMM状态转换图

车辆停入、驶出车位的波形和状态如图6,其中①为稳定状态,②为波动状态。可以看出,磁场数据剧烈波动时,都是车辆在停入和驶出车位的过程。但是稳定状态虽然磁场数据没有大幅度波动,却稳定在不同的数值附近。由于磁场环境量会随时间发生漂移,所以不一定低的数值就是无车状态,单纯根据稳定时的数值无法判断当前的稳定状态是有车还是无车。因此,在稳定状态的前一个波动状态,也无法简单根据数据变化判断是车辆停入还是驶出。

3.2 算法设计

车位检测算法的设计主要从HMM的特性考虑,可见状态的规律特性中可以找出隐藏状态。检测算法流程图如图7所示。

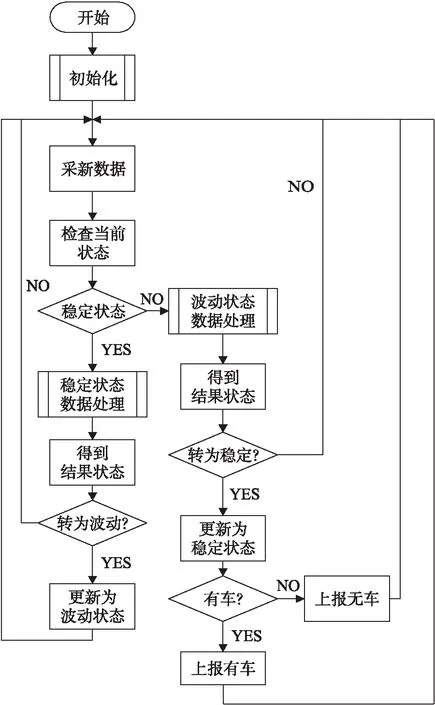
图7 检测算法流程图

检测节点安装完成后进行初始化操作,采集车位上无车时的磁场作为无车基线值,初始化完成之后进入数据处理过程。根据车位隐马尔可夫模型的分析,将磁场分为稳定状态和波动状态。稳定状态数据处理中包含状态转换判断、无车基线更新、稳定状态更正等操作。波动状态数据处理中包含状态转换判断、特征值组成、结果判断、结果输出等操作。

3.2.1 初始化算法

保证车位当前无车占用时,初始化操作令节点采集一段无车时磁场值作为背景值,是实现车位占用情况判断的重要依据。初始化流程如图8所示。

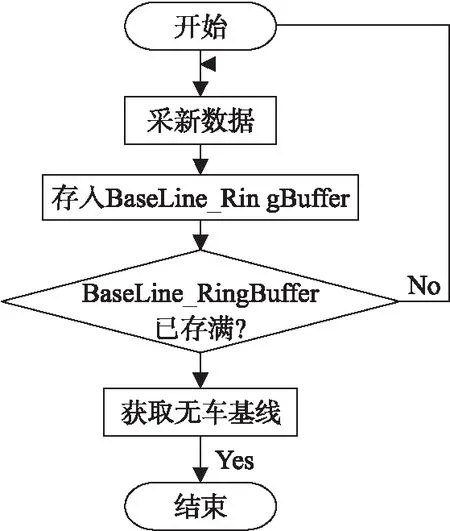
图8 初始化操作流程图

将检测节点安装好后,保持车位处于无车状态,发送初始化指令,启动初始化程序,传感器将采集车位无车时的地磁场数据,存入长度为n的容器BaseLine_RingBuffer,直到将其存满。

我们将当前车位无车时的磁场背景值称为基线值,即无车基线(BaseLine)。获取基线值的方法如式(1),给最新存入的数据点赋予最高的权值,更往前的数据权值依次降低,使基线既能更贴近当前环境磁场的变化,又不丢失历史数据信息。经过计算,获得的BaseLine[n]即为当前车位无车基线。

(1)

3.2.2 稳定状态数据处理

磁场处于稳定状态时,传感器仍按照3 Hz的采样速率继续采集磁场值。在稳定状态中,磁场保持稳定,无法提取较多的信息用于判断,我们在稳定状态处理过程中,操作过程较为简单。状态转换判断操作即判断当前磁场状态是否由稳定状态转换为波动状态,判断标志是连续1 s的每一个采样值和上一个采样值之差都超过了稳定转换到波动的阈值(StoF_TH),当稳定状态转换为波动状态,后续的磁场采样值都会进入波动状态处理过程。无车基线更新操作即在车位无车的稳定状态下,实时跟踪车位基线值,避免长时间的地磁场缓慢漂移引起一系列错误。稳定状态更正即在稳定状态中同时检测磁场值突变,避免上一个波动状态的判断错误导致后续判断无法纠正的问题。

稳定状态数据处理算法见算法1。其中车位信息包括包括当前状态、无车基线缓存器BaseLine_RingBuffer、稳定转为波动门限值StoF_TH、无车基线更新周期Update_Period、稳定状态更正周期Testify_Period、基线更新门限值Update_TH、稳定状态更正门限值Testify_TH等。

算法中NowToStandInc指新采样点NewData与基线BaseLine之差,反映了当前磁场与无车背景值之差;NowToBiasInc指新采样点NewData与磁场跟踪值之差,反映了当前磁场的突变情况;StandToBiasInc指磁场跟踪值与基线BaseLine之差,反映了磁场的偏移程度。

3.2.3 波动状态数据处理

波动状态持续时间一般比稳定状态短,而且波动状态结束之后的稳定状态必须通过算法重新判定是否有车。实际应用来说,只需要判断波动状态结束之后车位的状态是无车或有车,就能够达到车位检测的目标,因此不必要判断波动状态是车辆停入还是驶出车位。所以在本算法只判断图5中的“有车”和“无车”状态,对“车来”和“车走”状态不作判断。

波动状态数据处理过程见算法2。波动状态中,从波动状态开始至结束,算法需要记录整个过程中的特征值,包括时间、最大值、稳定之后的磁场平均值、稳定点当前磁场值等信息。确定车位从波动状态转为稳定之后,用上述信息获取用于车位状态判断的特征值位(FeatureByte,结合了多种停车过程特征量的特征组合值),通过查表获取判断结果。最终上报这一次波动状态完成后的判断结果,完成本次波动状态数据处理过程。

其中,FeatureByte的获取方法是将波动状态过程中的一些特征值通过处理之后,存入一个byte中,以供后续算法查表判断。我们将一些停车过程中的最典型的过程量结合,组成强特征值,用以表征明显的停车行为。

我们在室外温度6 ℃～30 ℃的条件下,进行了为期6个月,超过200次的停车数据采集实验,涉及车型包括SUV、三厢轿车、两厢轿车、电动汽车及不同品牌乘用车,通过正常倒车入库、正向停车和侧方位停车、多次反复停车、极慢或极快停车,以及东西南北不同朝向停车等实验,总结出有车和无车的强特征值表,如表1。

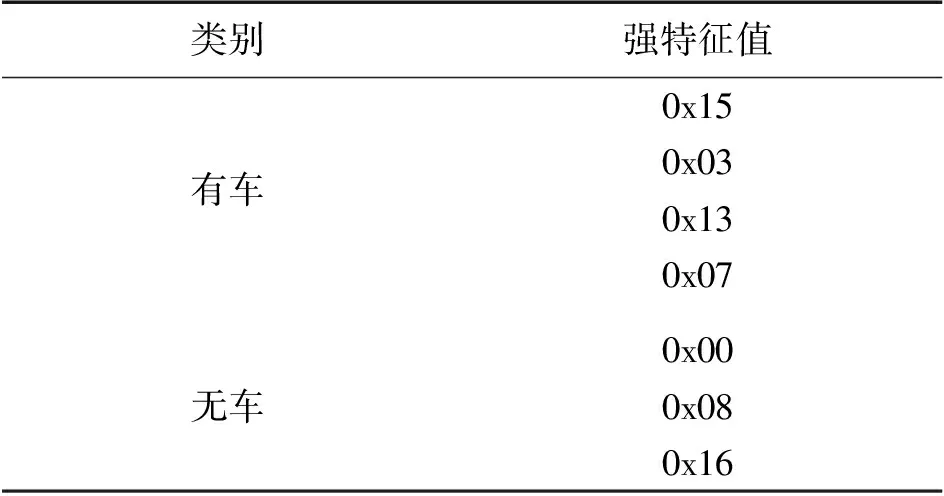
表1 停车状态强特征值表

车位检测系统在正常运行中,波动状态的特征量组成FeatureByte后通过查强特征值表,判断车位有车或无车。

组成FeatureByte的方法见表2。其中低五位是有效值,高三位是预留值,默认为0。

查表时如果能在强特征值表中找到结果,返回车位状态state(有车或无车),直接完成本次判断;如果不能在强特征值表中找到结果,则将结果state置为不确定状态(即当前停车过程量无法在实验所得结果中找到类似样本,需要后续算法判断当前状态),在算法2中进行后续处理。

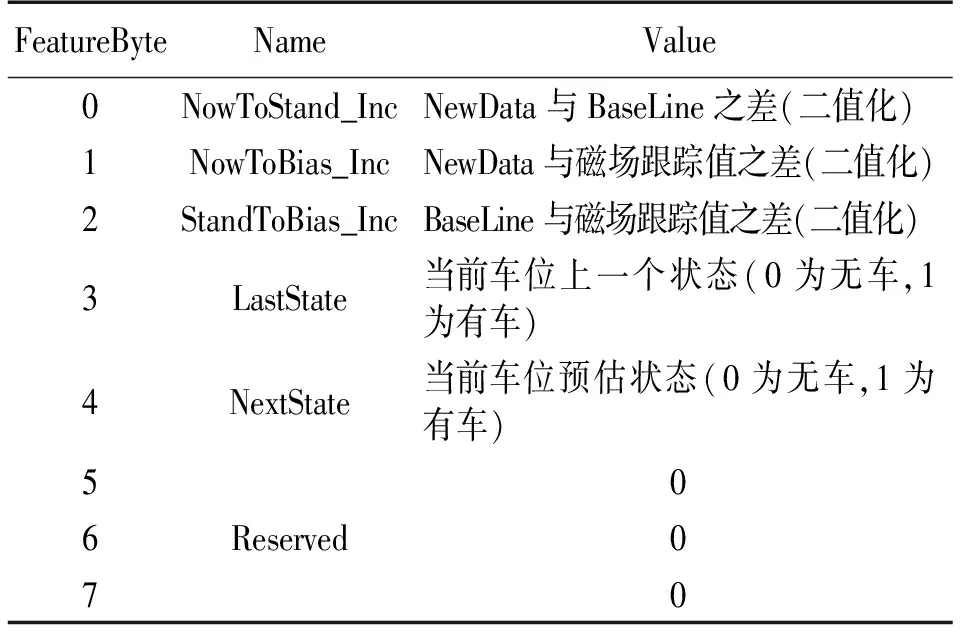
表2 FeatureByte组成方法

4 测试

为了验证本文所设计算法对于乘用车的检测准确率,我们在华中师范大学校内多个露天停车场进行了为期超过10个月的实际测试。测试过程中所涉及车辆与停车数据采集实验类似,包括各类常见的品牌和车型,停车过程同样包括倒车入库、正向停车、侧方位停车、斜方位停车,以及极快、极慢出入停车位或不按车位划线位置停车等各种行为。另外,除实验人员组织进行的测试外,我们还在车流量较大的九号教学楼露天停车场进行了真实环境测试,测试场景如图9所示。

图9 真实环境测试场地

我们在停车场上方安装了摄像头进行视频记录,作为车位检测的佐证,加上实验人员组织的停车实验数据,最终统计出所有的判断结果,如表3。可以得出算法准确率为98.11%,漏检率为1.13%,误判率为0.75%,较理想地完成了车位检测的目标。

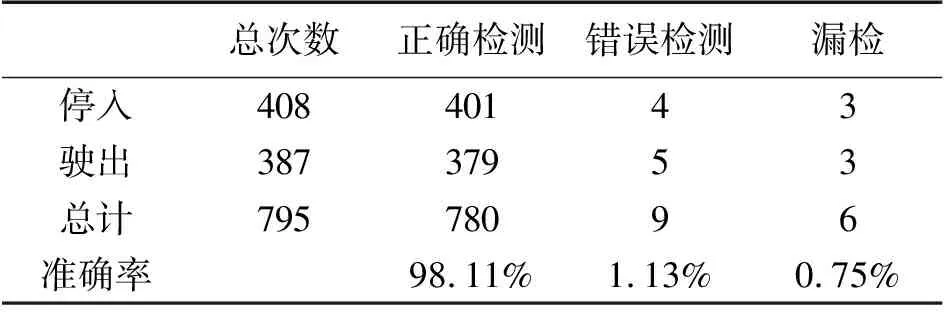
表3 测试结果表

经过实际检验,本文提出的车辆检测算法优于文献[14]中检测准确率97%、文献[15]中的96%、文献[16]中的96.4%等;同时,由于低功耗设计和大容量电池的使用,节点使用寿命得以延长;虽然由于使用了电感式磁传感器,比起当前大多数研究人员使用的磁阻式传感器增加了少量的生产成本,但是也带来了更高的鲁棒性。