一种应用于在线标定的可观测度分析方法*
2019-05-08杜滨瀚王海亮李国璋石志勇
杜滨瀚,王海亮,马 忠,李国璋,石志勇*
(1.陆军工程大学石家庄校区 车辆与电气工程系,石家庄 050003;2.中国人民解放军78616部队,成都 610214)
惯性器件误差是影响惯导系统导航精度的主要误差源,在导航前对系统进行在线标定是十分必要的[1-4]。目前标定过程中通常采用卡尔曼滤波器对器件误差进行估计,而状态量的可观测性直接影响滤波估计的效果。在线标定时载体通过进行各种特定的机动来激励各误差参数,提高系统的可观测性,从而使滤波器迅速收敛。因此,在设计卡尔曼滤波器之前必须对系统做可观测性分析,且可观测性分析对研究在线标定时各误差量的收敛情况与载体机动方式的关系具有重要意义[5-8]。
目前,基于分段线性定常系统PWCS(Piece-Wise Constant System)可观测性分析方法和基于奇异值分解SVD(Singular Value Decomposition)可观测度分析方法被广泛应用于惯导系统滤波估计前的可观测性分析[9-12]。为了能够将可观测性量化,文献[13]提出了可观测阶数和相对可观测度的概念,对PWCS可观测性分析方法进行了改进。文献[14-17]等也通过进一步分析可观测矩阵的奇异值和特征值,分别从不同的角度研究了状态的可观测度分析方法。
以上研究虽然能够判断系统的可观测性甚至能够得到系统的可观测度,但并不适用于惯导系统在线标定的需要,因为即使计算得出惯导系统完全可观测,也无法保证各误差参数的标定时间和标定精度符合标定要求,即误差参数的估计结果不一定都是可靠的,因此在分析系统可观测性的基础上,有必要进一步分析各误差参数的可观测度。
本文从算法原理上分析了PWCS可观测性分析方法和SVD可观测度分析方法的不足,并基于范数最优化受约束理论,提出一种新的可观测度分析方法并应用到在线标定的研究中。与之前的方法相比,该方法可以准确计算出每一个滤波状态量的可观测度,符合惯导系统在线标定的需求,具有较强的工程应用价值。
1 在线标定基本理论
1.1 在线标定滤波模型
本文以弹载捷联惯导系统的在线标定为例进行说明。惯性器件由于其工作原理、安装工艺的不完善以及使用环境的变化等均可造成传感器的输出误差,进而导致系统误差,由于安装误差在实验室标定后基本不随器件的老化而变化,因此这里只考虑惯性器件的常值零偏及刻度系数误差。以车载主惯导输出的速度和姿态信息作为匹配量,参照文献[18]建立系统误差的状态空间模型。
状态方程:

(1)
式中,状态变量为
X=[δVN,δVU,δVE,δΦN,δΦU,δΦE,φx,φy,φz,δkax,
δkay,δkaz,x,y,z,δkgx,δkgy,δkgz,εx,εy,εz]T
(2)
状态矩阵为
(3)
式中:
(4)
(5)
(6)
(7)
(8)
(9)
(10)

量测方程为
Z=HX+V
(12)
式中:V表示量测噪声;量测变量为
Z=[δVN,δVU,δVE,δΦN,δΦU,δΦE]T
(13)
量测矩阵为
(14)
1.2 系统可观测矩阵
由于系统的可观测性与噪声激励无关,将式(1)、式(12)给出的系统模型离散化可得:
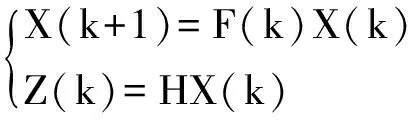
(15)
式中:X(k)∈Rn,F(k)∈Rn×n,Z(k)∈Rm,
H∈Rm×n。由式(3)可得:
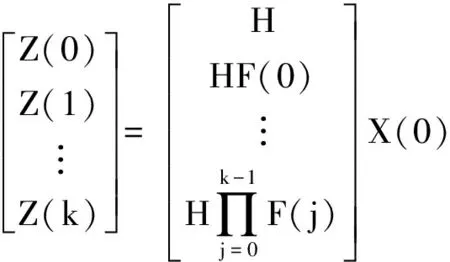
(16)

(17)
2 已有可观测性分析方法及不足
利用上节惯导系统滤波模型,从算法原理上分析PWCS可观测性分析方法和SVD可观测度分析方法,得出这两种算法用在惯导系统在线标定中都存在一定不足。
2.1 PWCS可观测性分析方法
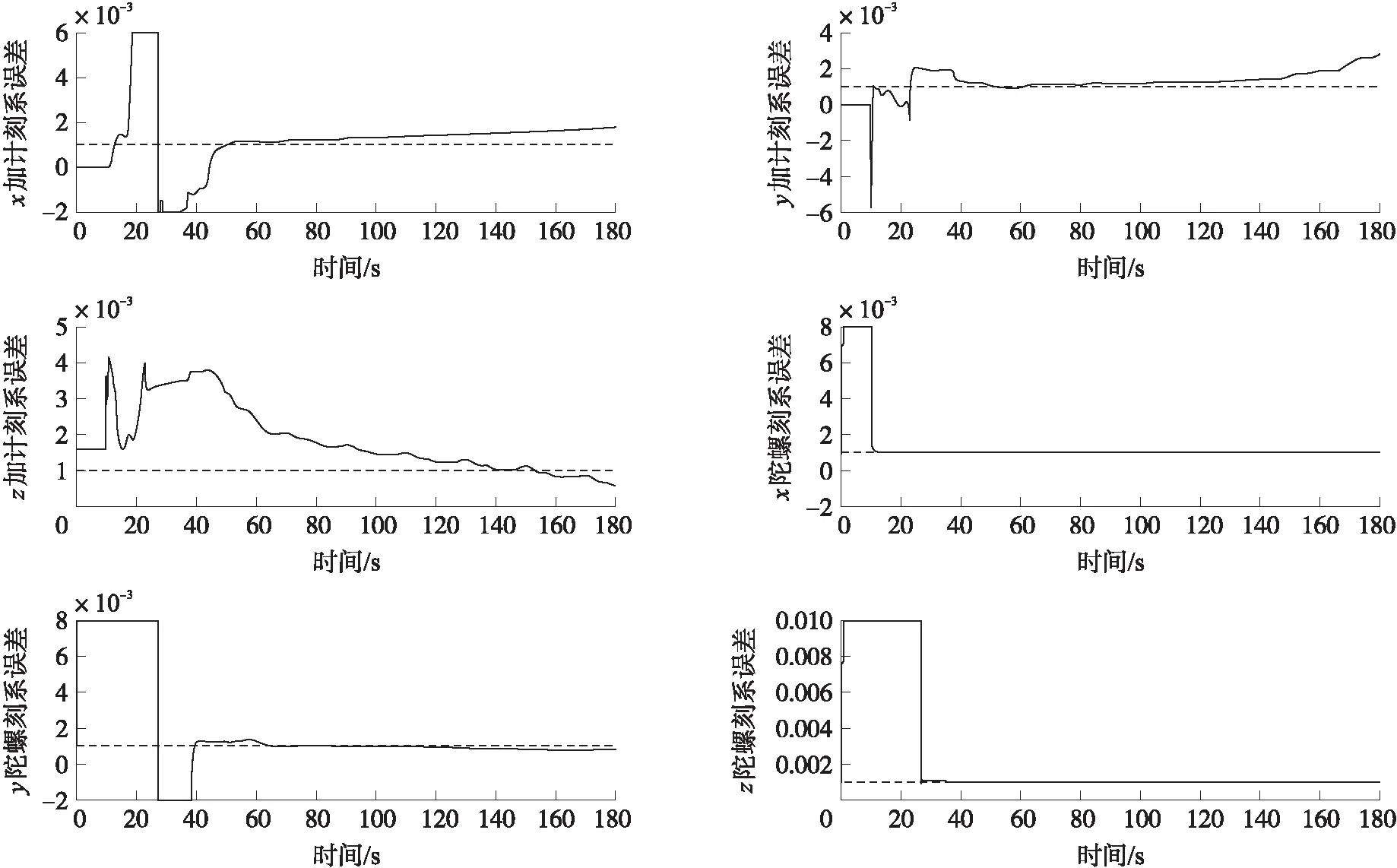
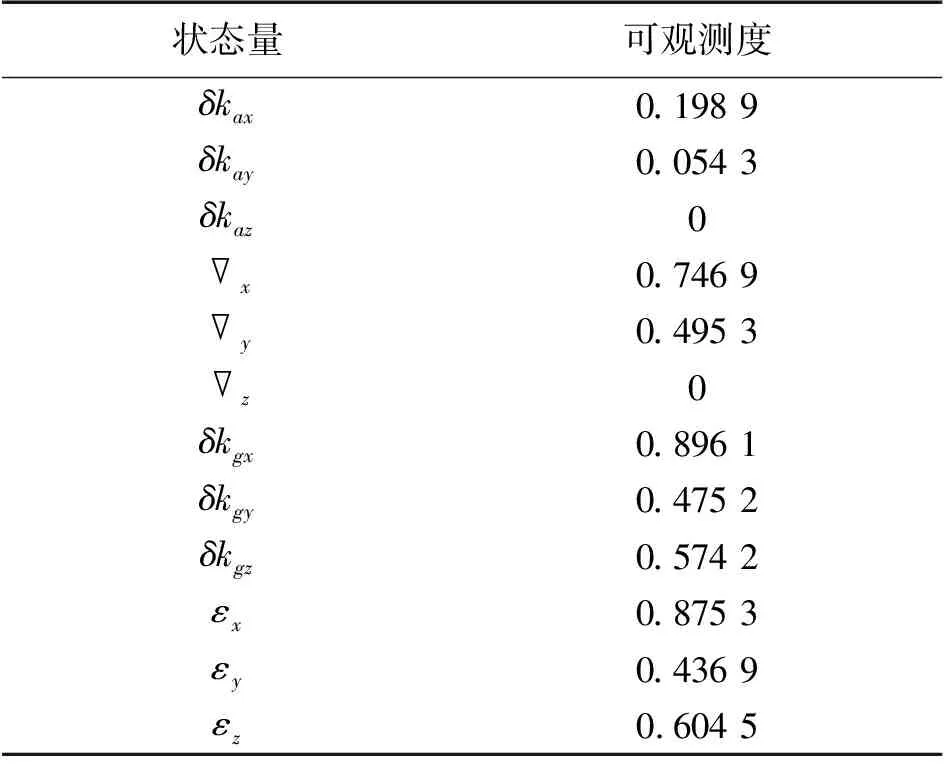
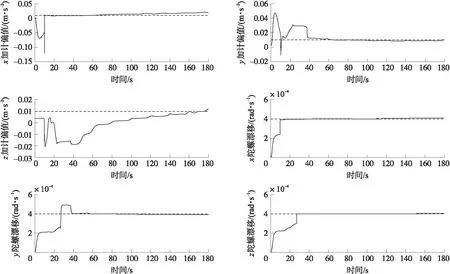
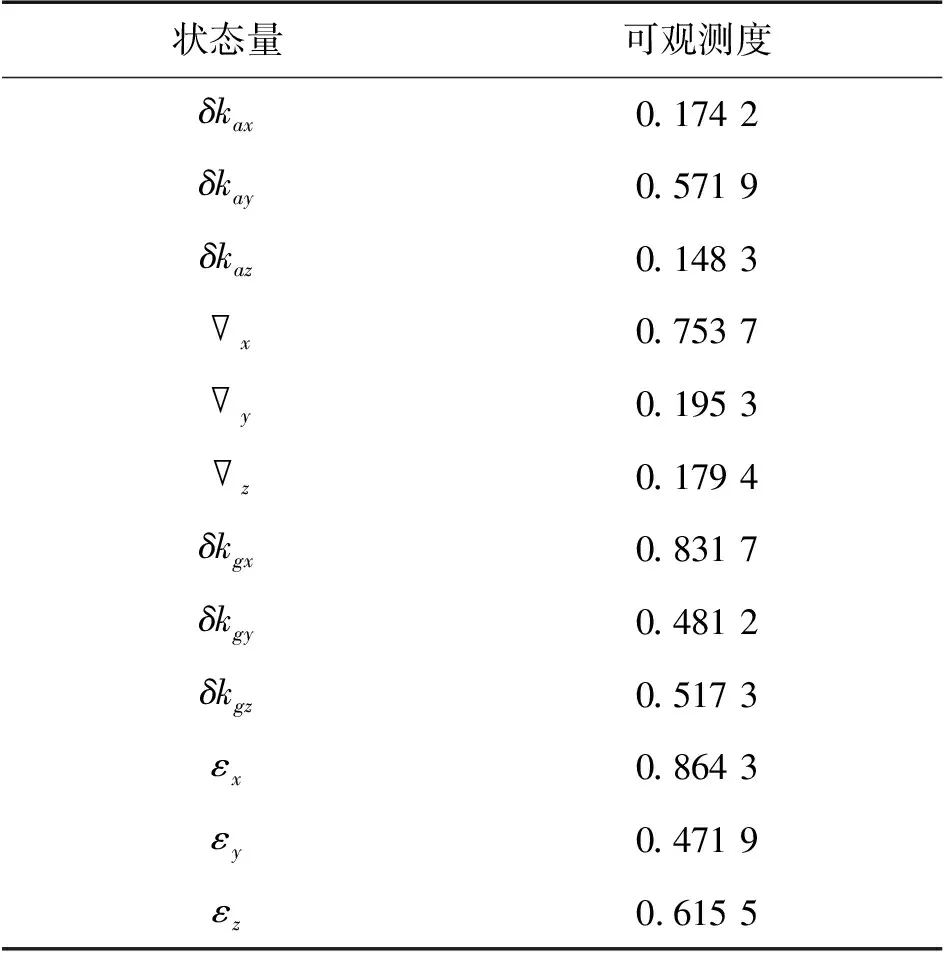
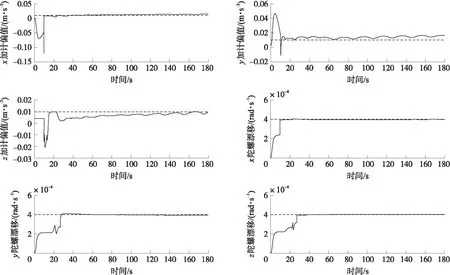
在对时变系统进行可观测性分析时,一般采用PWCS可观测性分析方法[19-20],其原理是将时变系统分成很多时间段,每段在很短的时间内当做定常系统处理,求出系统的可观测矩阵Q的秩并与系统的维数进行对比,如果rank(Q)=n,则系统完全可观;如果rank(Q) 针对PWCS可观测性分析方法的不足,东南大学提出了基于SVD的可观测度分析方法[21],该算法将可观测矩阵Q进行奇异值分解。 Q=USVT (18) 式中:U=[u1,u2,…,ul],V=[v1,v2,…,vn]分别为l阶和n阶的单位正交方阵,且S=diag(s1,…,sr,0,…,0)是l×n阶的矩阵,式中对角线元素满足s1≥s2≥…≥sr>0。将Q代入式(16)得 (19) 进而可得 (20) 利用量测向量Z,计算每一个奇异值si对应的状态向量X,si的值代表了相应的状态线性组合的可观测度。 根据该算法的原理可以得出SVD可观测度分析方法存在几点不足:①通过系统奇异值矩阵无法反应出各状态之间的耦合特征。②该算法仅能提供状态线性组合的可观测度,无法提供各独立状态参数的可观测度。 本文定义的可观测度是属于每一个状态量的,即每个状态量都存在一个对应的可观测度,参照第1节给出的系统模型,以第1个状态x1为例进行介绍。 将可观测矩阵Q改写为: Q=(qQ*) (21) 式中:q∈R(k+1)m×1,Q*∈R(k+1)m×(n-1)。 定义a∈R1×(k+1)m为任意一个行向量,γ为x1的可观测度,则由范数最优化受约束理论可得: (22) 状态的可观测度主要取决于可观测矩阵Q以及输出中各状态量对应的系数,如果一个状态能够通过系统的量测值准确的估计出来,则可以确定该状态是可观测的。 分析惯导系统的输出,由式(16)、式(17)、式(21)可得 (23) 假定a满足式(7)中的约束条件,则有 (24) 计算前首先对部分变量进行说明:定义矩阵Q∈Rl×n和(Q*)T∈R(n-1)×l,且Q的秩为r,(Q*)T的秩为r*;Null[(Q*)T]为一包含所有满足(Q*)Ta=0的a的向量空间,ψ1,…ψl-r*是 Null[(Q*)T]的一组单位正交基;向量a与向量q之间的夹角为θ,向量q在空间Null[(Q*)T]上的投影为β,向量β与向量q之间的夹角为ϑ。 为了后面计算方便,在此给出如下两个引理。 引理1当a平行于β时,θ取最小值,且最小值为ϑ。 以上引理均比较容易证明,由于篇幅有限,在此省略证明过程。 由上文对变量的定义可知,向量a与向量q之间的夹角为θ,则有: (25) 进而可得: (26) 考虑引理2-1,可得: γ=cosϑ (27) 由式(10)可以得出0≤γ≤1,根据前文的分析,可得出以下结论: γ越靠近1,代表状态x1的可观测度越强,状态x1的估计精度越高,估计速度越快,反之则说明状态的可观测度越弱,估计精度越差,估计速度越慢。 考虑到ψ1,…,ψl-r*是Null[(Q*)T]的一组单位正交基,则有: (28) 由于β为向量q在空间Null[(Q*)T]上的投影,则有 (29) 结合式(10)可得: (30) 考虑引理2-2,如果γ* (31) 如果γ*=l,那么γ=0。 显然,此算法能够得到每一个状态量的可观测度γ,对惯导系统在线标定研究中的载体机动路径设计具有很强的指导意义。 为了验证本文提出的可观测度分析方法的特点及准确性,在设计在线标定机动路径的基础上,利用MATLAB搭建仿真平台进行仿真验证。 参照文献[22]提出的在线标定机动路径设计原则,针对火箭炮设计一条机动路径,具体如表1所示,惯性器件初始误差参数设置如表2所示。 设载体所在初始纬度为30°,经度为118°,杆臂r取[2 3 2]m,状态变量X初值都设为0。滤波各初始矩阵设定值如(32),(33)所示,仿真时间180 s,采样频率0.01。 Q0=diag{(5×10-5g)2,(5×10-5g)2,(5×10-5g)2,(0.05°)2,(0.05°)2,(0.05°)2,01×15} (32) R0=diag{(0.01 m/s)2,(0.01 m/s)2,(0.01 m/s)2,(0.01°)2,(0.01°)2,(0.01°)2} (33) 表1 炮车机动路径 表2 惯性器件参数设置 为了说明本文提出的可观测度分析方法能够得出每一个状态量的可观测度的特点,首先利用基于SVD分解的可观测度分析方法计算动态系统的可观测度,其结果如表3所示。 表3 基于SVD分解的可观测度分析方法分析结果 图1 加速度计和陀螺仪刻度系数误差估计曲线图 从表3可以看出,采用该方法只能得出相关耦合状态的可观测度,其中有一组状态组合的可观测度为零,说明该系统是不完全可观测的,但是无法确定具体哪个状态可观测,哪个状态不可观测,导致不能有针对性的对标定路径进行调整。 下面采用本文提出的新的可观测度分析方法计算个状态量的可观测度,结果如表4所示。 由计算结果可以得出:①δkaz和z的观测度为0,该系统并不是完全可观测的。②不可观测的状态有δkaz、z,其余均可观测。③δkgx、δkgz、εx、εz的可观测度较强,即估计精度高且估计速度快,而δkax、δkay的可观测度低,即估计精度差或者估计速度较慢。 该分析方法能够明确得出各状态量的可观测度,根据各状态可观测度的值即可有针对性的修改机动路径以更好的激励惯性器件误差。 表4 新的可观测度分析方法分析结果 图2 加速度计零偏和陀螺仪漂移误差估计曲线图 为了验证本文提出的可观测度分析方法的准确性,利用MATLAB软件平台对惯性导航系统在线标定过程进行仿真,采用标准卡尔曼滤波方法进行参数估计,参数估计结果如图1、图2所示,其中直线为预先设定值,曲线为滤波估计值。 如图1、图2所示,Z加速度计的刻系误差及零偏误差无法收敛,X加速度计和Y加速度计的刻度系数误差收敛速度较慢且精度一般,其余误差参数都能够快速高精度收敛,这与前面的可观测度分析是一致的,证明了新的可观测度分析方法的准确性。 参照新的可观测度方法计算得出的各状态量的具体可观测度,有针对性的对机动路径进行调整,设计炮车在机动至13s~27s时通过一拱桥,以激励Z轴加速度计的输出,修正后的具体机动路径如表5所示。 表5 修正后炮车机动路径 对载体机动路径调整后,采用新可观测度分析方法分析系统可观测度结果如表6所示。 表6 修正路径后新的可观测度分析方法分析结果 按照修正后的机动路径对系统误差进行激励,通过仿真得到的惯性器件在线标定结果如图3、图4所示。 由图3、图4可以看出,修改机动路径后,Z加速度计的刻系误差及零偏误差能够迅速收敛,且精度较高,其余误差参数也都能迅速收敛,说明修正后的机动方式能够有效激励惯性器件全部误差参数,再一次证明了本文可观测度分析方法的准确性。 直线为预先设定值,曲线为滤波估计值图3 加速度计和陀螺仪刻度系数误差估计曲线图 直线为预先设定值,曲线为滤波估计值图4 加速度计零偏和陀螺仪漂移误差估计曲线图 本文在分析PWCS可观测性分析方法和SVD可观测度分析方法原理特点及不足的前提下,基于范数最优化受约束理论提出了一种新的可观测度方法并将其应用于弾载捷联惯性器件的在线标定中。该方法能够分析得出每一个滤波状态量的可观测度,能够给惯导系统的在线标定机动路径设计提供足够的依据,完全适用于惯导系统的在线标定需求。仿真试验表明,利用该算法计算得到的每一个状态量的可观测度与标定中状态量的滤波收敛特性具有一致性,证明了该算法的正确性,具有较强的工程实际意义,可为火箭炮的制导化改造研究提供一定技术支持。2.2 SVD可观测度分析方法
3 新的可观测度分析方法
3.1 可观测度算法简介

3.2 可观测度的计算


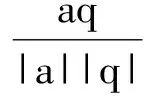

4 仿真试验
4.1 初始条件设置


4.2 基于SVD分解的可观测度分析方法分析结果

4.3 新的可观测度分析方法分析结果
4.4 在线标定仿真结果及分析
4.5 修改机动路径后仿真结果分析


5 结束语
