水下CMUT动态性能仿真与测试的研究*

张 睿,解 丹,马健喆,潘理虎,张永梅,陈立潮

(1.太原科技大学计算机科学与技术学院,太原 030024;2.北京华龙通科技有限公司,北京 100083; 3.北方工业大学计算机学院,北京 100144)

超声传感器作为水下探测系统的核心部件,它的性能和相关技术制约着整个水下探测技术的优化及发展。超声传感器在微加工技术的驱动下,逐渐发展为小型化和多功能集成化。电容式超声传感器CMUT(Capacitive Micromachined Ultrasonic Transducer)便是在这一趋势下的一种新型传感器。相比于传统压电式超声传感器,CMUT具有小体积、轻重量、低成本、低功耗、高可靠性、宽频带、频率易于控制、易于集成阵列、易于电路集成、易于批量制造等优点[1-4]。因而在水下超声波传感器的研究和应用中,CMUT已成为一个新的热点。

本文针对CMUT的优越性,对一种应用于水下探测的CMUT动态性能仿真与测试进行了研究。由于ANSYS对CMUT动态性能仿真分析时需要较长的运算时间,且操作复杂,运算效率也低等,故本文在介绍CMUT的基础结构和工作原理后,运用SIMULINK动态仿真和分析CMUT的发射及接收性能,以提高CMUT的设计效率。最后,通过实验平台的搭建,既对仿真实验的有效性进行了验证,又对CMUT传感器的性能进行了测试。实验证明,本文的研究有利于本国新型超声换能器的进一步改进及发展。

1 CMUT基本结构及工作原理

CMUT阵列属于多层复合结构。多个敏感单元构成一个阵元;而多个阵元又构成一个CMUT阵列。图1是敏感单元的结构,从上到下依次是进行图像化处理的金属Al上电极、氧化硅隔离层、振动薄膜、密闭真空腔体、氧化硅绝缘层、硅衬底以及金属Al下电极[5]。其中,振动薄膜由SOI片的顶层硅制成并被刻蚀了隔离槽,真空腔是通过氧化硅刻蚀而成。CMUT既能发射信号又能接收信号,两种情况下,都需要在敏感单元的两电极上施加直流偏置电压(DC)[6-7],由于DC产生的静电力,敏感单元振动薄膜会被拉向极板的下端,然后由于其反向回复力而达到平衡状态。此时如果将特定频率的交流激励电压(AC)施加到薄膜上,则薄膜将发生挠曲,同时辐射的超声波将引起极板间电容变化并有微弱的电流信号产生,这些信号经跨阻放大等电路的处理被转化为电压信号,最终信号被接收。

图1 CMUT敏感单元结构

2 CMUT敏感单元设计

在设计CMUT的固有频率和尺寸时,要考虑微加工工艺的水平、应用领域、成本等因素。影响探测的两个关键因素是探测的距离和探测的分辨率,而探测的分辨率与CMUT的频率正相关。考虑到超声波的频率越高会使得传播过程中衰减越多,传播的距离也会越短,因而,在CMUT水下探测中需要选取恰当的工作频率。一般而言,在水下使用200 kHz～600 kHz频率的换能器可以对10 m～40 m以内的物体进行探测。本文为了对10 m之外的物体进行探测,同时需要获取较高像素的图像,因而选用工作频率为200 kHz～600 kHz的CMUT。CMUT敏感单元可以被视为半径为a、厚度为tm的圆形薄板。由于薄板在密度为ρl的液体中的固有频率表达式[8]如式(1):

(1)

式中:杨氏模量E=169 GPa,泊松比σ=0.29,密度ρ=2 332 kg/m3,内部张力T=20 MPa,外部压力p=1 Pa且CMUT薄膜的材料为硅。

通过MATLAB获得的CMUT薄膜振动频率与半径和厚度之间的关系如图2所示,可以得到,薄膜半径变化范围为:30 μm～100 μm,薄膜厚度变化范围为:2 μm～5 μm,薄膜半径的减小或厚度的增加将会导致谐振频率增大,并且薄膜厚度对频率具有较大的影响。

图2 薄膜振动频率与半径和厚度之间的关系

综合以上给出的参数范围,以及大气压和水压下的最大位移、机电转化系数、Si-SOI键合工艺条件,加之,课题组前期对ANSYS有限元分析方法的研究[9-11],最终所确定的CMUT敏感单元的主要结构参数如表1。

表1 CMUT敏感单元主要结构参数 单位:μm

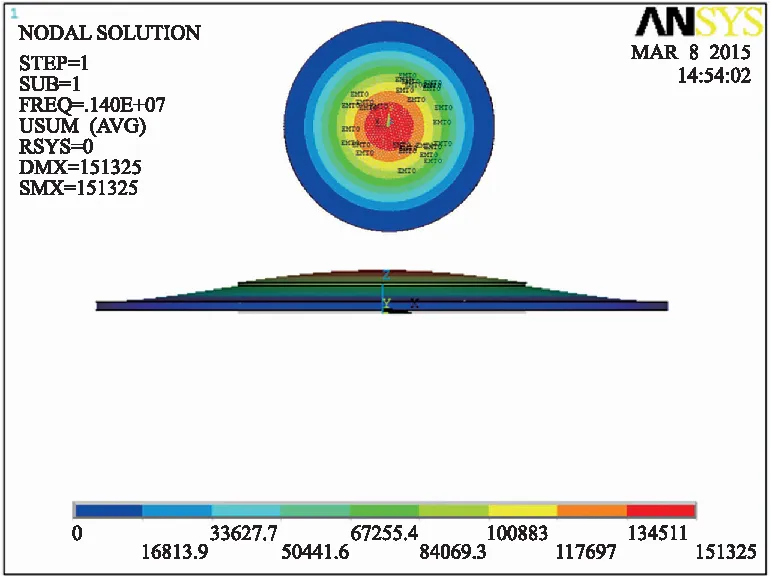
图3 CMUT振动薄膜一阶模态图

为了获得CMUT薄膜振动的相关特性参数,运用力学参数对CMUT振动的主要结构——振动薄膜进行建模、分析。结合表1,本文通过观察ANSYS模态仿真得到的振动薄膜工作振型,确定CMUT的谐振频率,从而确定其工作频率。如图3所示,CMUT振动薄膜的一阶谐振频率为1.40 MHz,振动过程中,振动薄膜的中心部分上下往复运动,同时周边部分在中心部分的带动下也进行上下往复运动,但中心部分的振动幅值是最大的。此振动模式符合CMUT的发射和接收模式。应用中,为避免外载荷和器件谐振频率一致而产生共振,从而造成结构屈服,将其频率设为谐振频率的1/5～1/3[12],故将其频率设在400 kHz左右的范围中。

3 SIMULINK动态性能仿真与分析

目前,一般用有限元分析软件ANSYS对CMUT敏感单元进行动态仿真和分析。此软件其存在一些问题如:难以操作、运算耗时长、效率低等。为了避免这些问题,本实验在MATLAB下采用SIMULINK工具建立状态方程模型,为了对敏感单元的发射和接收性能模拟与分析,构建了一个CMUT动态系统。同时,为了方便建模,在忽略薄膜固有的高阶振动模式并认为薄膜本身的回复力是线性的、弹簧系数为一个常量且进行活塞式运动的假设下,CMUT结构被简化为一个如图4所示的平行板电容器模型,其中下电极是固定的、上电极是可垂直移动的。模型中,重为m的质量块代表敏感单元的薄膜,弹性系数为keq的弹簧代表薄膜自身的反向回复力,阻尼因数为b的阻尼器代表薄膜振动过程中所损耗的能量,初始状态时极板的间距为g0。

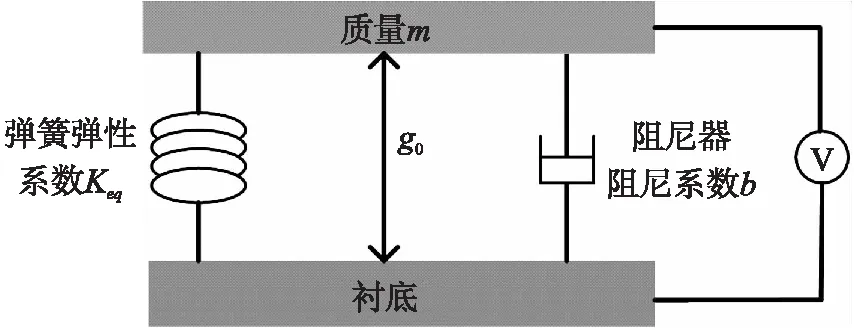
图4 平板电容模型图

假设敏感单元薄膜位移的变化是w,根据牛顿第二定律得到,薄膜所受力的总和是:

(2)

3.1 发射性能建模、仿真与分析

CMUT处于发射模式时,发射声压是主要的性能参数,其定义如式(3)所示。在该公式中,Zm表示介质的阻抗,ω表示角频率,A表示超声波的振幅,其等效于薄膜的振幅。由此式可以得出,发射声压正比于薄膜的振幅,又AC随振动薄膜振幅的增大而增大,故发射声压和AC之间是正相关的。在这种模式下薄膜主要受大气压力、静电力、薄膜本身的回复力和阻尼力的影响。由式(2)得式(4)。

Pa=Re(Zm)ωA

(3)

(4)

图5 CMUT发射模式SIMULINK模型

发射模式的顶层模型如图5(a)所示,可以准确的表现CMUT的工作情况,其包括输入、输出和子系统1(子系统2和3)。子系统1、2和3的模型如图5(b)、5(c)和5(d)。图5(c)由静电力表达式建立,DC和AC构成输入电压。图5(d)中,薄膜所受到的外力被转化为振动薄膜的位移和速度,为了对振动薄膜的位移做限制,增设了限位模块,此模块受CMUT腔中绝缘层厚度的影响。此外,假设CMUT受到的环境压强为标准大气压(atm=1.013×105Pa)。在仿真中,仿真结束时间设为4.0×10-6s,固定步长设置为1.0×10-9s,并在MATLAB的M文件中定义模型中的各参数。

一般情况下,将薄膜平衡位移下降至真空腔高1/3时所受到的VDC值设置为塌陷电压的临界值[13]。本文真空腔高为0.8 μm,1/3腔高为0.267 μm。当敏感单元的两电极仅施加有DC,没施加AC时,薄膜下降位移与DC之间的关系如图6所示。

图6 薄膜位移与DC的关系

可以看出,当DC最初施加在薄膜上时,薄膜会有较大的位移变化,但是随着薄膜本身回复力的作用,位移很快趋于稳定,并达到平衡。另外,薄膜平衡位移随着DC变大而变低。当施加40 V、43 V、45 V的DC时,薄膜平衡位移分别约为0.243 μm、0.257 μm、0.266 μm。由于0.266 μm最接近0.267 μm,故将CMUT敏感单元的塌陷电压设定为0.266 μm所对应的45 V的DC值。

图7 工作电压对薄膜位移的影响

DC和AC对薄膜振动位移的影响情况如图7所示。在该图中,薄膜的位移到达稳定状态后会呈现出周期性的变化。当薄膜被施加恒为25 V的DC时,薄膜的振动幅度随着AC的增大而增大;当薄膜被施加恒为25 V的AC时,薄膜振动幅度的随着DC的增大而增大,但薄膜的平衡位移却随DC的增大而降低。可以看出,DC和AC对薄膜振幅产生的影响相比,DC的产生影响较小,且薄膜振动位移在DC=20 V,AC=25 V的情况时最大。

在DC和AC的总和低于塌陷电压时,本文用Simulink对发射声压在不同施加电压下的变化情况进行了仿真、分析。如图8所示,可以看出发射声压在DC=20 V,AC=25 V时最大。

图8 不同工作电压下的声压特性

图9 CMUT接收模式SIMULINK模型

3.2 接收性能建模、仿真与分析

CMUT工作在接收模式下SIMULINK顶层模型如图9(a),由输入、输出和子系统1构成。子系统2的模型如图9(c),其根据静电力公式建立。子系统3的模型如图9(d),其依据式(3)给出,子系统3上的限位模块,能够对薄膜塌陷的情况进行较好的仿真。为了实现对不同结构CMUT参数的快捷调用,在M文件中,定义了子系统1、2和3中的参数。子系统4的模型如图9(e)根据电流式(5)建立。

(5)

要完整的模拟超声波的传播过程是非常复杂的,本文为了方便分析,仅是使用一个16个周期正弦激励信号来表示这种现象。当大气压强和外界声压作用在被施加了45 V的DC的薄膜上时,如图10(a)显示了当SIMULINK用于模拟16个周期的正弦激励信号时薄膜动态位移的变化,如图10(b)是激励信号产生的电流,图中薄膜的平衡位移大约是0.167 3 μm,振幅大约是0.013 4 μm;电流的振幅大约是8.062 5×10-11A。

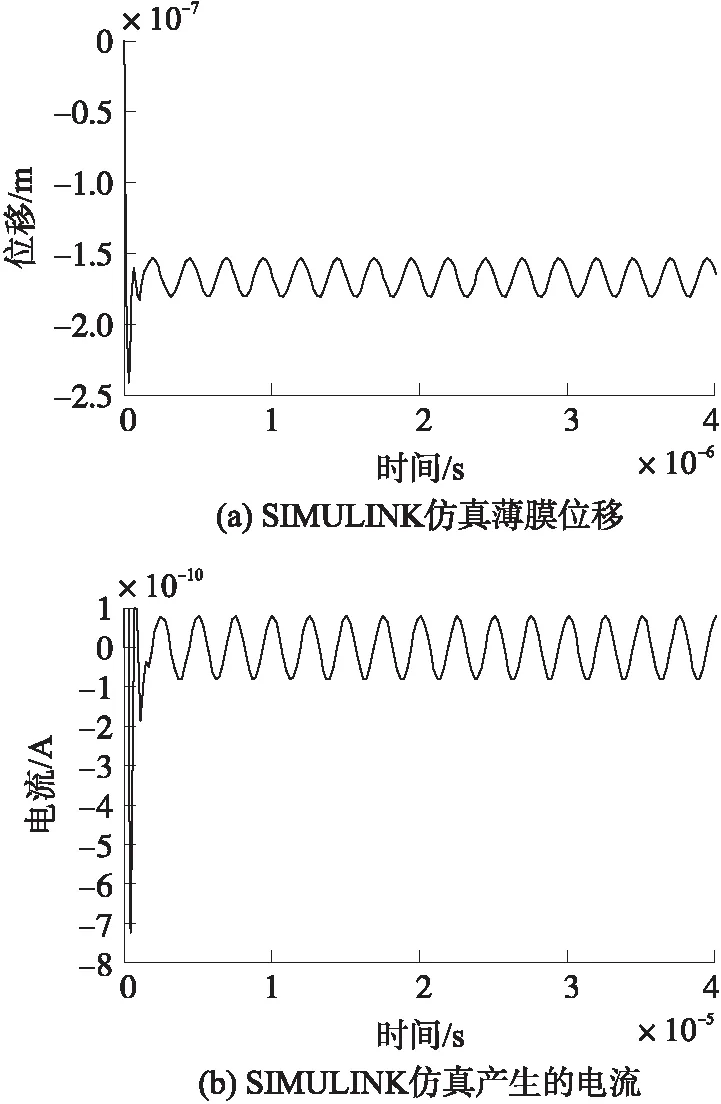
图10 SIMULINK仿真结果

4 实验测试

4.1 塌陷电压及激励条件

为确定实际的塌陷电压,本文利用安捷伦精密阻抗分析仪(Aglient4284A)对加工之后的CMUT进行C-V特性曲线分析。根据上述SIMULINK动态系统仿真,确定塌陷电压设置为45 V,步长设置为 1 V,一个循环过程为:DC由0 V变化至45 V,再从45 V变化到-45 V,之后从-45 V返回到最初的 0 V。测试时进行两次循环,结果如图11,可知CMUT的重复性较好且没有迟滞性,在DC从40 V变化到 -40 V 期间,两次循环获得的电容曲线的变化几乎一致,并且电容随着DC的变化而变化;其次,当DC在(40 V,45 V)和(-40 V,-45 V)之间时,薄膜的电容基本不再发生改变,因此认为此区间的薄膜已经发生塌陷且实际塌陷电压为40 V。与SIMULINK动态分析确定的塌陷电压相比,40 V较低于45 V,有可能是由于SIMULINK仿真是在标准大气压的条件下展开的,忽略了封装材料和各种环境压力对CMUT的影响。

图11 CMUT C-V曲线

为进一步确定在总和为40V的电压下AC和DC的最优组合,实验中将CMUT与标准传感器放置于距离为60 cm的同一水平高度。其中,CMUT是发射器,传感器在放置之前已被校准。激励信号设置成5周期的正弦信号,频率设为400 kHz,步长设为2 C,此条件下逐渐改变传感器的激励条件。测试结果如图12,当AC和DC都是20 V的情况下,CMUT被最大限度的驱动,其发射性能也达到最好。

图12 不同驱动条件下CMUT发射声压图

图13 三目标B超探测

4.2 CMUT阵列水下 B超探测

本文搭建了如图13(a)所示的探测实验平台。测试中,CMUT收发一体驱动电路的直流电源由吉时利2231A-30-3供给,且设置为±6 V;CMUT工作时的直流电源由固纬GPS-4303C供给,且设置为±20 V;20 Vpp的激励信号(2-cycles,400 kHz)由信号发生器供给。实验时将收发一体CMUT固定于实验箱一侧进行水平线性扫描,扫描间隔为2 cm,目标体1、2、3底面分别是正方形、圆形和矩形,其中,正方形的边长为1 cm、圆的半径为1.5 cm、矩形的长、宽分别为5 cm和3 cm。最终的探测结果图如图13(b)。图中正方形和长方形底面的探测较清晰,而圆形底面的探测面较模糊,3个目标体的探测的位置和实际摆放的位置相符,并且由目标体形成的三角形轮廓的边长分别为29.5 cm、24.6 cm和42.8 cm,接近扫描环境中的实际状况,较好的呈现出水中目标体的轮廓和位置,对水下CMUT探测进行了基本的实现。

5 总结

本文对水下电容式微超声换能器的动态性能展开仿真与测试。在对CMUT敏感单元模型、结构及尺寸介绍的基础上,本文使用SIMULINK对CMUT的发射及接收性能进行动态仿真分析,并在SIMULINK下建立CMUT动态系统,然后在此系统中利用模型模拟CMUT的发射性能和接收性能,对CMUT的设计、分析和应用有着重要的理论参考意义;此外本文结合仿真结果,搭建测试的平台,对加工封装好后的CMUT开展C-V特性及探测测试,在验证CMUT仿真方法有效性的同时,也初步实现了水下探测。此研究对后续CMUT的设计及测试方法的优化具有一定的参考价值。