高温高压对微波破岩效果的影响模拟研究

2019-05-08马兰荣李丹丹韩艳浓

石油钻探技术 2019年2期

胡亮，马兰荣，谷磊，李丹丹，韩艳浓

（中国石化石油工程技术研究院，北京 100101）

石油钻井过程时常会钻遇玄武岩、花岗岩等坚硬岩石层，普遍存在机械钻速慢、钻头磨损严重等问题，大大增加了钻井成本和施工风险[1]。因此，亟待解决钻遇坚硬岩石层时的提速增效问题[2-4]。国外提出了一种微波辅助破岩技术，在钻头破碎岩石之前先采用微波照射岩石对其进行预加热，使其内部产生微裂纹，降低岩石强度，以利于钻头破碎岩石[5-8]。此后，国内外开展了相关的理论研究和室内试验工作：F. Hassani 等人[9]通过有限元模拟分析了微波照射对岩石单轴强度的影响；斯伦贝谢公司设计了不同微波照射通道的微波辅助破岩钻头，并申请了相关专利[10]；戴俊等人[11]在室内进行了微波照射花岗岩试验，发现花岗岩经微波照射后，其抗拉强度明显下降，验证了微波对岩石的作用效果；卢高明等人[12]研究了微波照射参数对微波破岩效果的影响，室内试验证明了微波高功率短时间照射更容易使岩石破裂。但上述研究都基于常温常压环境，未考虑异常温度和压力对微波破岩效果的影响，而实际钻井过程中井底的温度和围压要明显高于地面且变化剧烈，因此要将微波破岩技术应用于石油钻井领域，就必须考虑井下高温高压对微波破岩的影响。为此，笔者采用数值模拟方法，分析了井下高温高压对微波破岩的影响，以期获得影响规律，为微波破岩时调整微波参数提供理论依据。

1 微波破岩理论

被照射物体吸收微波的功率密度与微波照射参数和被照射物体的电磁参数有关[13]，其计算公式为：式中：P为物体吸收微波的功率密度，W/m3； ε′′为被照射物体的电磁介电损耗因子；f为微波照射频率，Hz； ε0为真空介电常数，8.854×10-12F/m；Ei为被照射物体内部电场有效值，V/m。

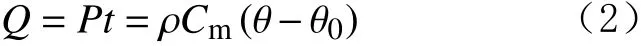
物体被微波照射一定时间，其吸收的能量为[14-15]：式中：Q为被照射物体吸收微波的功密度，J/m3；t为微波照射时间，s； θ0为物体在微波照射前的温度，℃； θ为物体在微波照射后的温度，℃； ρ为物体密度，kg/m3；Cm为物体比热，J/（kg·℃）。

被照射物体温度上升速度为：

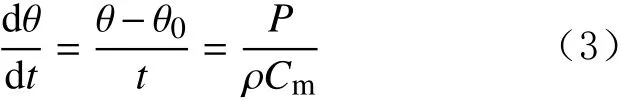
将式（1）代入式（3），得到物体温度变化与微波照射的关系式：

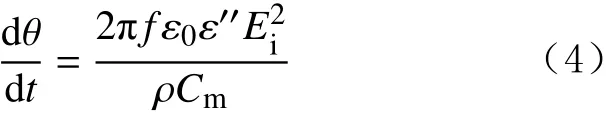
物体在微波加热后，温度变化所引起的应变可以表示为[16-18]：

式中： ε为物体应变量； α为热膨胀系数，1/℃； Δθ为温度变化量，℃。

由热量产生的应力可以通过胡克定律计算：

式中： σ为热应力，Pa；E为弹性模量，Pa；v为泊松比。

2 微波破岩数值模拟

2.1 模拟模型的建立

岩石由多种矿物成分组成，根据不同矿物成分对微波的吸收特性，可将其分为吸波成分和透波成分2 大类。笔者根据涪陵页岩气田焦石坝区块钻遇某层段岩石的矿物成分，建立了岩石二维平面模型，如图1 所示。该模型由方解石和黄铁矿组成，方解石的介电损耗因子约为4×10-4，黄铁矿的介电损耗因子为17。因此，模拟时可以认为方解石为透波材料，不吸收微波能量；黄铁矿是吸波材料，吸收微波能量。模型中黄铁矿颗粒随机散布于基质方解石当中，其体积占模型总体积的10%。

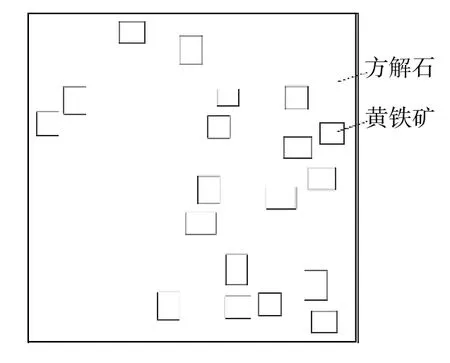
图 1 岩石二维平面模型Fig. 1 Two-dimensional plane model of rock

2.2 模拟条件及参数

采用有限元软件进行模拟，设定微波功率密度为6×106W/m3，照射时间为120 s。模拟实际钻井工况，设置模型初始条件为温度120 ℃，围压30 MPa。模型边界为固定约束，周围环境产生热交换，热交换系数设为50 W/（m2·℃）。模型中不同矿物成分的热学和力学参数见表1—表3[13]。

2.3 模拟结果

2.3.1 模型温度分布

模型的温度分布如图2 所示，温度梯度分布如图3 所示。

表 1 岩石各成分的热膨胀系数Table 1 Thermal expansion coefficients of various rock components

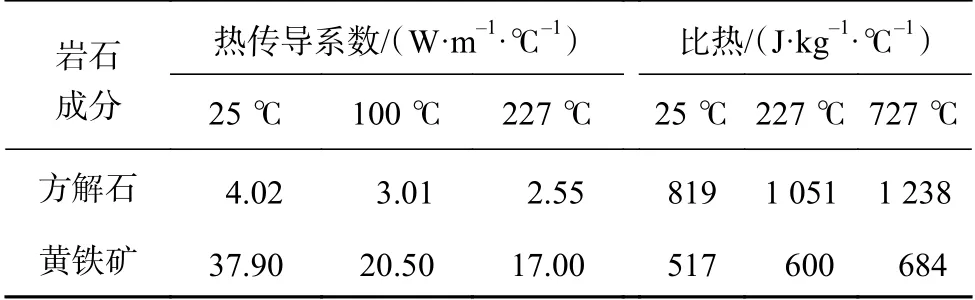
表 2 岩石各成分在不同温度下的热传导系数及比热Table 2 Thermal conductivity and specific heat of various rock components at different temperatures

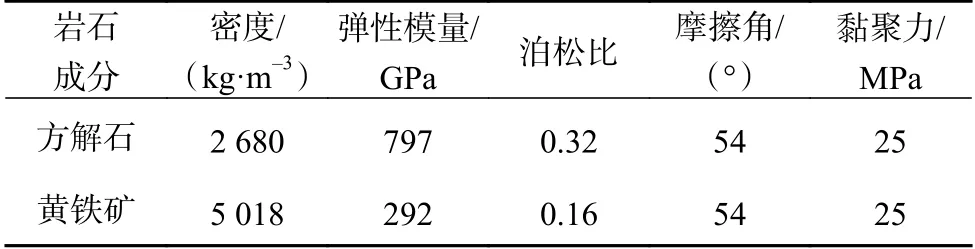
表 3 岩石各成分的力学参数Table 3 Mechanical parameters of various rock component

图 2 模型的温度分布Fig. 2 Temperature distribution of the model

从图2 可以看出，模型右下角黄铁矿密集区温度最高，而模型左下角方解石密集区温度最低。分析认为，这主要是因为黄铁矿为吸波材料，吸收微波能量后温度急剧升高；而方解石为透波材料，温度升高主要依靠高温黄铁矿的热传递作用，从而形成了温度由黄铁矿密集区向方解石密集区扩散的现象。

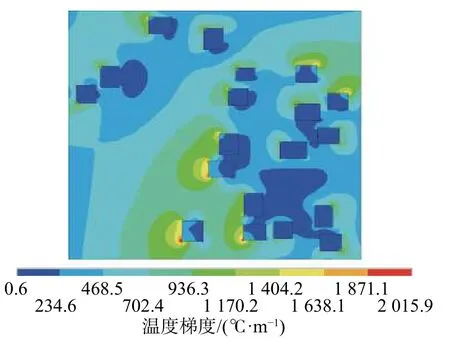
图 3 模型的温度梯度分布Fig. 3 Temperature gradient distribution of the model

从图3 可以看出，黄铁矿内部温度梯度最低。分析认为，这主要是因为微波对黄铁矿是整体加热的，黄铁矿内部温度升高幅度基本相等，温度几乎没有差异，因此温度梯度最低。自身不升温的方解石包裹在剧烈升温的黄铁矿周围，必然会造成二者接触面的温度差很大，因此此处温度梯度最大。

2.3.2 模型应力及塑性变形

模型的应力分布如图4 所示。

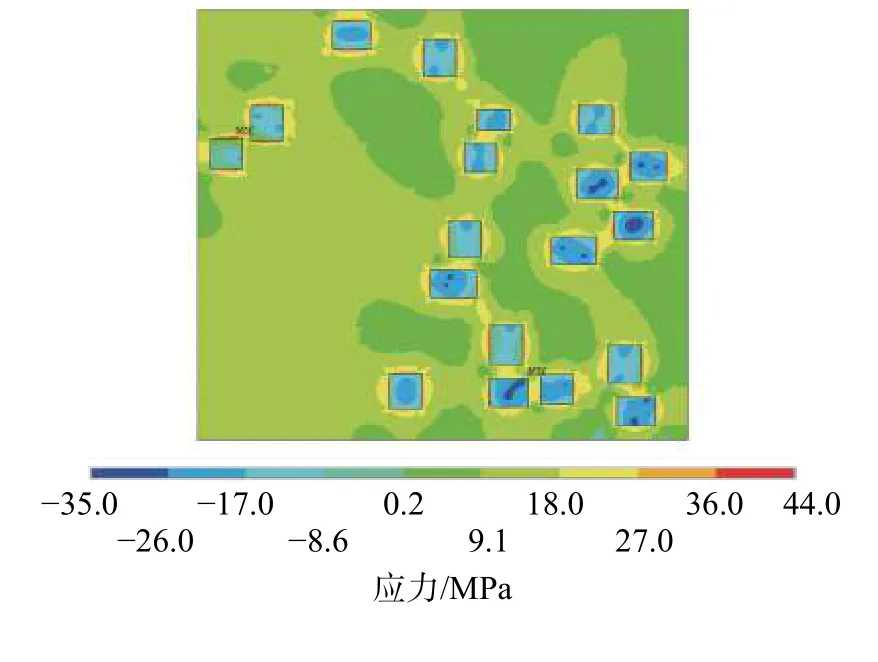
图 4 模型的应力分布Fig. 4 Stress distribution of the model

从图4 可以看出：黄铁矿颗粒热应力主要为压应力（负值），其中心处最大；方解石热应力主要为拉应力（正值），且最大值环绕黄铁矿颗粒分布。由于岩石的抗拉强度远小于抗压强度，故方解石更容易受拉产生破坏。因此，在微波照射下，当方解石局部最大拉应力大于方解石自身抗拉强度时，将会产生破坏。

岩石是一种脆性材料，模拟中当有限元某节点发生微小位移时，就可以认为是发生了塑性变形，也就意味着发生了破坏。因此可以通过模拟模型的塑性变形情况来表征微波照射下岩石的破裂情况。笔者选用Drucker-Prager 屈服准则，模拟模型的塑性变形，结果如图5 所示。

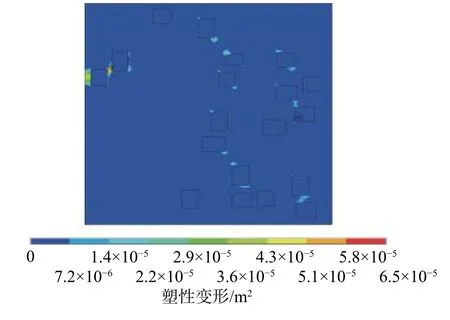
图 5 微波照射下模型的塑性变形Fig. 5 Plastic deformation of the model under microwave irradiation

从图5 可以看出，模型大部分为深蓝色区域，位移为0，意味着没有发生塑性变形，塑性变形主要集中在黄铁矿颗粒周边，与图4 中的最大拉应力分布相对应。因此，微波照射岩石造成的主要破坏方式是黄铁矿颗粒周围的方解石受拉破坏。

3 破岩效果影响因素分析

3.1 温度

以上分析可知，岩石破坏主要发生在黄铁矿颗粒周围，也是整个模型中最先发生破碎的区域。当外界环境参数变化时，这个区域最为敏感。因此，选取黄铁矿边缘处的方解石某节点为研究对象，分析温度变化对微波破岩的影响。方解石某节点温度增幅和温度梯度随环境温度的变化曲线如图6 和图7 所示。

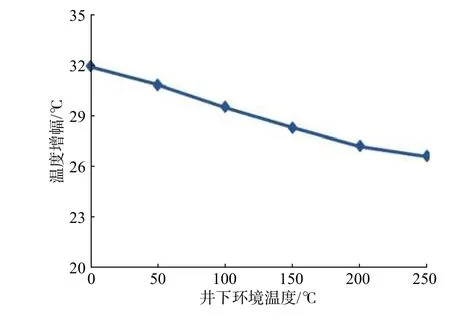
图 6 不同环境温度下方解石某节点的温度增幅Fig. 6 Temperature amplification of a node in calcite under different ambient temperatures

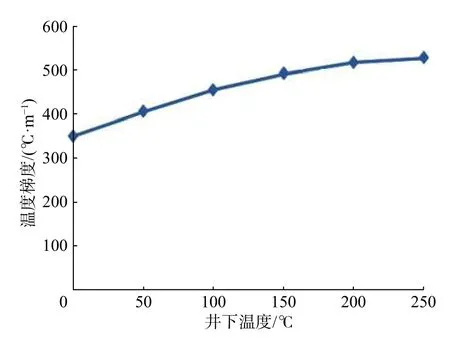
图 7 不同环境温度下方解石某节点的温度梯度极值Fig. 7 Temperature gradient extremum of a node in calcite under different ambient temperatures

从图6 和图7 可以看出，随着环境温度提高，方解石某节点的温度增幅逐渐减小，而温度梯度逐渐增大。分析认为，这主要是因为方解石的比热随环境温度升高而增大，导致吸收相同热量时的温度增幅减小，进而使温度梯度增大。

模拟不同环境温度下方解石某节点发生塑性变形的时间，结果如图8 所示。

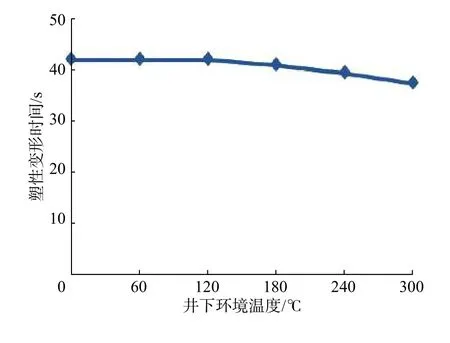
图 8 不同环境温度下方解石某节点的塑性变形时间Fig. 8 Plastic deformation times of a node in calcite under different ambient temperatures

从图8 可以看出，随着温度升高，方解石某节点发生塑性变形的时间变短，微波破岩效率提高。

利用最小二乘法对图8 中的曲线进行拟合，得到岩石塑性变形时间与井下环境温度的关系式为：

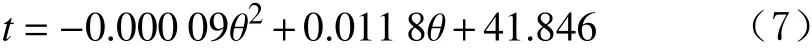
式（7）的相关指数R2为0.988 7，利用式（7）可以计算出0～300 ℃条件下方解石某节点发生塑性变形的时间，有利于现场快速判断井下温度变化对微波破岩效果的影响。

3.2 围压

由图4 和图5 可知，应力极值和塑性变形主要发生在黄铁矿颗粒周围，因此选取黄铁矿边缘处的方解石某节点，模拟其在不同围压下的应力变化和塑性变形情况，分析井下围压变化对破岩效果的影响，结果如图9 所示。

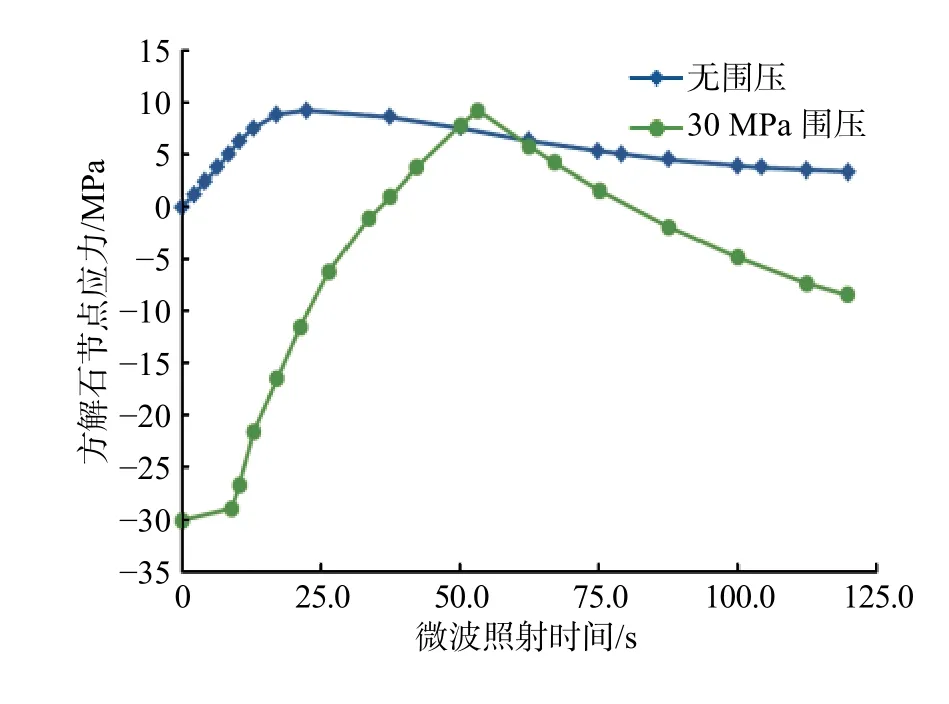
图 9 施加围压前后方解石某节点的应力对比Fig. 9 Comparison on the force of a node in calcite before and after confining pressure

从图9 可以看出，施加围压前后方解石某节点的拉压应力变化趋势类似；但不同之处在于，施加围压后，方解石某节点的应力从压应力逐渐转化为拉应力，而不是从0 开始。分析认为，这主要是由于受围压作用，岩石各部分最初都处于受压状态。因此，方解石某节点的受力是先由围压造成的受压逐渐转化为微波作用下的受拉。图9 中应力转折点是某节点处发生塑性变形的时间点，施加围压情况下这个时间点也比未加围压的时间点“晚”很多。

模拟不同围压下方解石某节点发生塑性变形的时间，结果如图10 所示。从图10 可以看出，随着围压增大，岩石塑性变形时间增长。图10 中曲线的拟合公式为：

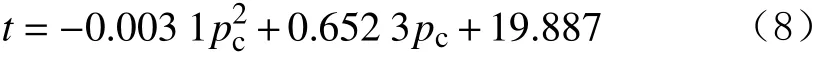
式中：pc为围压，MPa。

式（8）的相关指数R2为0.997 8，利用式（8）可以计算出围压0～70 MPa 条件下方解石某节点发生塑性变形的时间，有利于现场快速判断井下围压变化对微波破岩效果的影响。

3.3 高温高压共同作用

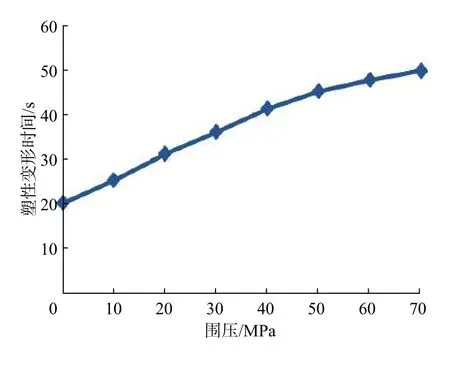
图 10 不同围压下方解石某节点的塑性变形时间Fig. 10 Plastic deformation times of a node in calcite under different confining pressures

地层温度和压力随埋深增加而升高，但由于不同区域的地质情况不同，地层温度梯度和压力梯度差异很大。为了研究温度和围压同时作用对微波破岩效果的影响，在一定假设条件下进行了模拟分析。

假设地面温度为20 ℃，地层温度梯度为3 ℃/100m，地层压力梯度为1 MPa/100m，模拟井深为2 000.00 m（温度80 ℃，围压20 MPa）、3 000.00 m（温度110 ℃，围压30 MPa）、4 000.00 m（温度140 ℃，围压40 MPa）、5 000.00 m（温度170 ℃，围压50 MPa）、6 000.00 m（温度200 ℃，围压60 MPa）和7 000.00 m（温度230 ℃，围压70 MPa）情况下微波照射后岩石发生塑性变形的时间，结果如图11 所示。

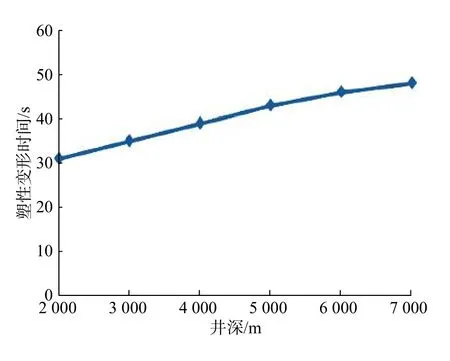
图 11 不同温度和围压作用下方解石某节点的塑性变形时间Fig. 11 Plastic deformation times of a node in calcite under different temperature and confining pressure

对比图11 和图8、图10 可以发现：温度和围压共同作用下岩石发生塑性变形时间的变化趋势与围压单独作用下的情况类似，井深5 000.00 m 以浅（温度170 ℃，围压50 MPa）的岩石塑性变形时间也基本相同；井深5 000.00～7 000.00 m、温度超过170 ℃时，塑性变形时间小于单一围压作用下的时间，温度的影响开始体现，并与温度单独作用的影响趋势相吻合。由此可知，井下微波破岩过程中，围压的影响是主要的，要密切关注地层压力的异常波动，及时调整微波参数；温度的影响主要体现在高温情况下，地层温度异常升高、钻开地热储层或开采干热岩时要予以关注。