直线形单排管冻土帷幕平均温度计算
2019-05-08刘阳辉洪泽群韩延广
刘阳辉,洪泽群,韩延广
(1.同济大学 地下建筑与工程系,上海 200092; 2.同济大学 岩土及地下工程教育部重点实验室,上海 200092; 3.上海市隧道股份有限公司,上海 200232)
在人工地层冻结技术运用过程中,需要对冻土结构进行力学分析计算,此时通常假设冻土为均质介质,选用冻土帷幕平均温度所对应的物理力学参数作为均质假定下冻土结构材料参数。因此冻土帷幕的平均温度不仅仅是冻结效果的重要判据,也是确定冻土力学参数,进行冻土帷幕承载力评估的重要依据。
目前常用的平均温度求解方法有:积分法、等效截面法、经验公式法。积分法是利用已有的温度场解析公式,对冻土区域进行积分求解,直接求得平均温度。由于温度场的解析公式较为复杂,积分求解的难度较大,目前这一方法的研究较少。等效截面法是以冻结壁某一横截面的平均温度来代表整体冻结壁的平均温度,诸如笔者所提出的利用等效三角形法、等效梯形法、等效抛物弓或梯形-抛物弓叠合得到的特征截面处的平均温度来代替帷幕的平均温度[1-4]。单排管冻结平均温度等效计算的基础是巴霍尔金的温度场解析公式,因此计算准确性得到保证,但截面的选取和计算过程较为繁琐。经验法求解冻土帷幕的平均温度也是一种可行办法。陈文豹、汤志斌基于大量实测数据,给出了计算平均温度的“成冰公式”[5],但该公式过于保守,适用性较差[6],汪仁和等学者根据数值计算结果拟合出平均温度的计算公式[7],笔者根据等效截面计算公式形式也给出了平均温度的经验公式[8]。
目前,直线排管冻结温度场解析解主要有巴霍尔金单排、双排[9]和笔者的三排管稳态温度场解析解[10],这些解有较高的准确性[11-12]。本文将以笔者采用边界分离法得到的单排管冻结稳态温度场解析解为基础[13-14],采用积分法推导平均温度的直接计算公式。
1 单排管冻结稳态温度场解析解
单排管冻结的模型如图1所示。在单排管的管间距相等,冻结管表面温度相等情况下,笔者利用边界分离法得到稳态温度场解析公式(1)[14]:
(1)
式中,T(x,y)为任意点(x,y)的温度,℃;Tf为冻结管外表面温度,℃;ξ为冻土帷幕厚度之半,m;l为相邻冻结管间距,m;r0为冻结管外半径,m。
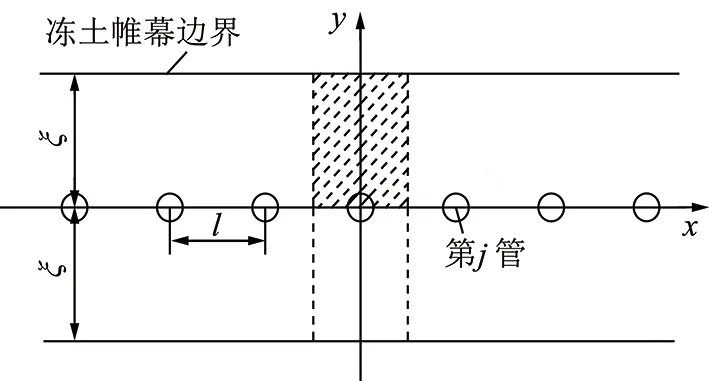
图1 单排管冻结模型Fig.1 Model of single row-piped freezing
式(1)按照工程实际参数近似处理可以简化成巴霍尔金的单排管冻结温度场解析公式。
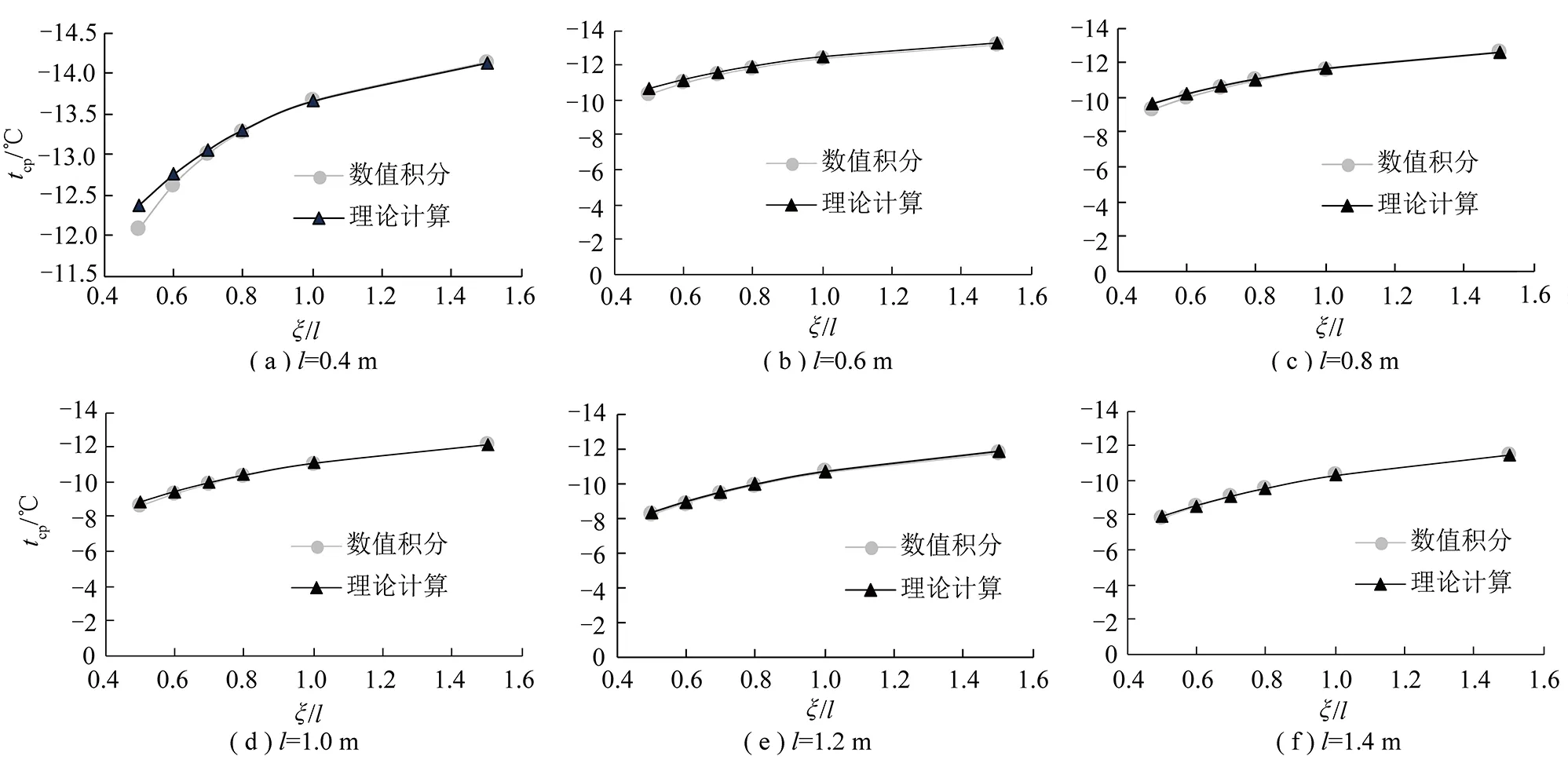
由图1所示,根据模型的对称性,冻土帷幕的平均温度tcp为T(x,y)在给定区域(-l/2 (2) 把式(1)代入式(2),得到单排管冻结平均温度的计算式。 (3) 式(3)主要问题是积分 (4) 利用贝塞特求和公式[15],得 (5) 对式(5)的积分部分进行分部积分,得到积分结果为 再次运用贝塞特求和公式,得 上式积分项在积分区间(-l/2 (6) 其中,X为区间(-l/2,l/2)内的某个实数。 将式(6)代入式(3),得到单排管冻结冻土帷幕平均温度为 (7) 考虑到土层的冻结温度T0的单排管冻结平均计算公式为 T0 (8) 在冻结后期,有πξ/l>1,所以ch(2πξ/l)远大于cos(2πX/l),得ch(2πξ/l)-cos(2πX/l)≈ch(2πξ/l)-1,式(8)可简化为 (9) 在上述推导过程,积分区域包含了冻结管部分,实际土层的平均温度的计算不应包含上述区域。同时,由于T(x,y)在冻结管圆心(0,0)处的取值趋于无穷,无法确定冻结管处的温度对积分结果的影响。因此需要对式(9)进行修正,减小偏差。 由于曲线积分较为困难,修正将采用已有积分策略对矩形区域(-r0 (10) 上述修正是对矩形区域(-r0 本文推导的平均温度计算公式是基于单排管冻结的稳态解析解,并根据实际工程对一些参数进行了简化,因此需要对解析公式的准确性进行研究。本文ANSYS进行热学数值计算,来研究公式的准确性和精度,确定计算公式的适用范围,即ξ/l满足什么条件时,理论计算较为精确。 考虑到单排管冻结布管形式的对称性,计算选取1/4区域,如图2所示。土性参数选取根据《上海地区人工冻土物理力学性能试验及其应用技术研究报告》[16],主要参数的取值初始温度为-20 ℃;冻土导热系数为172 W/(m·K);未冻土导热系数为122 W/(m·K);比热容为1.65 kJ/(kg·℃)。冻结参数根据常见情况,取Tf=-30 ℃,T0=0 ℃,r0=0.054 m,选用管间距l=0.4,0.6,0.8,1.0,1.2,1.4 m,考虑ξ/l=0.5,0.6,0.7,0.8,1.0,1.5共6种冻结发展状态。图3为l=1.0 m,ξ/l=0.8计算结果的温度云图。理论计算采用式(11),计算结果见表1,其中绝对误差为理论计算与数值计算结果的差值。 图2 计算模型Fig.2 Calculation model 图3 l=1.0 m,ξ/l=0.8的温度云图Fig.3 Contour plot of calculation results 将修正公式和数值计算的结果进行比较,如图4所示。 根据计算结果及对比,得到以下结论。 (1)理论计算结果与数值计算结果较为吻合。所完成的算例中,平均温度的误差小于0.5 ℃,随着冻土厚度的发展,理论计算结果与数值计算结果的差值逐渐减小。 (2)针对第2节提出得矩形修正区域与冻结管的差集,在常见布管参数条件下,该区域对计算结果的影响是有限的。这片区域的土体温度约为-30 ℃,面积约为0.001 3 m2。取最不利情况(冻土区域最小),l=0.4 m,ξ=0.2 m计算。这片区域造成的误差约为0.47 ℃,随着冻土厚度的发展,误差逐渐减小。同时,这块区域对理论计算的影响是提高平均温度,使计算结果偏向安全。因此采用矩形区域进行修正是可行的。 表1 计算结果Table 1 Calculation results 图4 结果对比Fig.4 Calculation results (1)基于单排管冻结稳态温度场解析解,本文采用积分法推导出冻土帷幕平均温度的直接计算公式,并对在冻结管附近的计算进行了修正。 (2)根据算例,随着冻土厚度的发展(相对厚度的增大),理论计算结果与数值计算结果的差值迅速减小到0.5 ℃以内,当相对厚度大于0.6时,对比计算结果的差值小于0.2 ℃。当相对厚度为1及以上时,差值小于0.1 ℃。通过数值模拟验证了平均温度计算公式的准确性,也说明公式简化和修正的合理性,公式计算的误差满足工程应用的要求。2 单排管冻结平均温度的计算
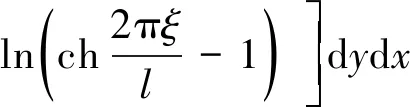
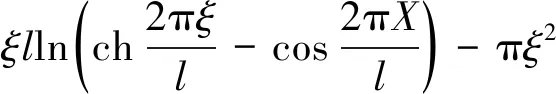
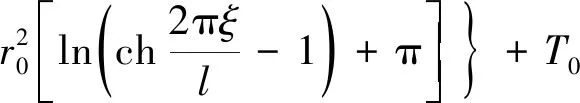
3 解的准确性



4 结 论
