船载转塔装置随动系统动力学建模与仿真

姜俊峰， 李伟， 赵维， 周晓军

(1.浙江大学 流体动力与机电系统国家重点实验室， 浙江 杭州 310027；2.浙江大学 浙江省先进制造技术重点实验室， 浙江 杭州 310027； 3.西北机电工程研究所， 陕西 咸阳 712099)

0 引言

船载转塔装置(STE)是一种常见的船载装置，可执行登陆火力支援、中近程防空、打击海面集结方力量等任务，对来袭导弹、射程内的飞行目标和处于潜望深度的潜艇，可以进行有效的干扰和毁伤。随动系统是STE的重要组成部分，可根据火控系统计算的射击诸元实时跟踪目标[1]。舰船受到风、浪、流等各种因素的综合作用，摇摆幅度大，结构参数时变性强，工况十分恶劣[2-3]。为了消除舰船摇摆和目标运动的影响，随动系统必须连续不断地调整瞄准线的方向角和俯仰角[4]，导致随动系统输出力矩变化剧烈，给随动系统的分析和设计带来了困难。因此建立STE随动系统的动力学模型，对影响随动系统输出力矩(下文简称“随动力矩”)变化的因素做定量分析，是十分必要的。

国内外对机载[5]、车载[6-8]、重型车辆[9]等随动系统的研究较为深入，建立了随动系统的运动学和动力学模型，对两轴稳定的交叉耦合力矩、耦合引起的角速度和稳定精度进行了研究和探讨[10-13]。但是STE的动力学研究仅停留在物理建模和简单的方程组数学建模阶段[4,14]，在简化问题的同时降低了动力学分析的精确度，而关于STE随动系统完整的动力学建模与随动力矩分析文献则尚未查到。

本文根据STE的结构特点,建立了随动系统的拉格朗日动力学模型,并在此基础上对随动力矩进行了仿真分析，仿真结果对STE随动系统的设计提供了理论依据。

1 坐标系定义

本文研究的STE随动系统是两轴稳定方案，由方位轴和俯仰轴构成。STE随动系统结构及坐标示意图如图1所示。为了分析方便，建立如图1所示4个坐标系：

1)大地坐标系Onxnynzn. 原点On位于船体重心，Onxn轴平行于水平面指向正北方，Onyn轴平行于水平面指向正东方，Onzn轴垂直于水平面指向下方。

2)船体坐标系Obxbybzb. 原点Ob与船体重心重合，Obxb轴平行于夹板面指向船首，Obyb轴平行于夹板面指向右舷，Obzb轴垂直于夹板面指向下方。

3)方位坐标系Ohxhyhzh. 原点Oh位于转塔重心，为了分析问题方便并不失一般性，设转塔重心位于转塔方位轴上；Ohxh轴平行于转塔回转平面，并与发射管轴线在一个平面内，Ohyh轴平行于转塔回转平面指向船首位置，Ohzh轴垂直于转塔回转平面指向下方。

4)俯仰坐标系Opxpypzp. 原点Op由Oh在3个坐标轴上各平移一定距离得到。Opxp轴与发射管轴线重合、指向射出方向，Opyp轴与俯仰轴重合、指向船首方向，Opzp轴垂直于Opxp、Opyp构成的平面向下。需要注意的是，在射击过程中，随着火箭弹数目的变化，发射管的重心会发生变化。

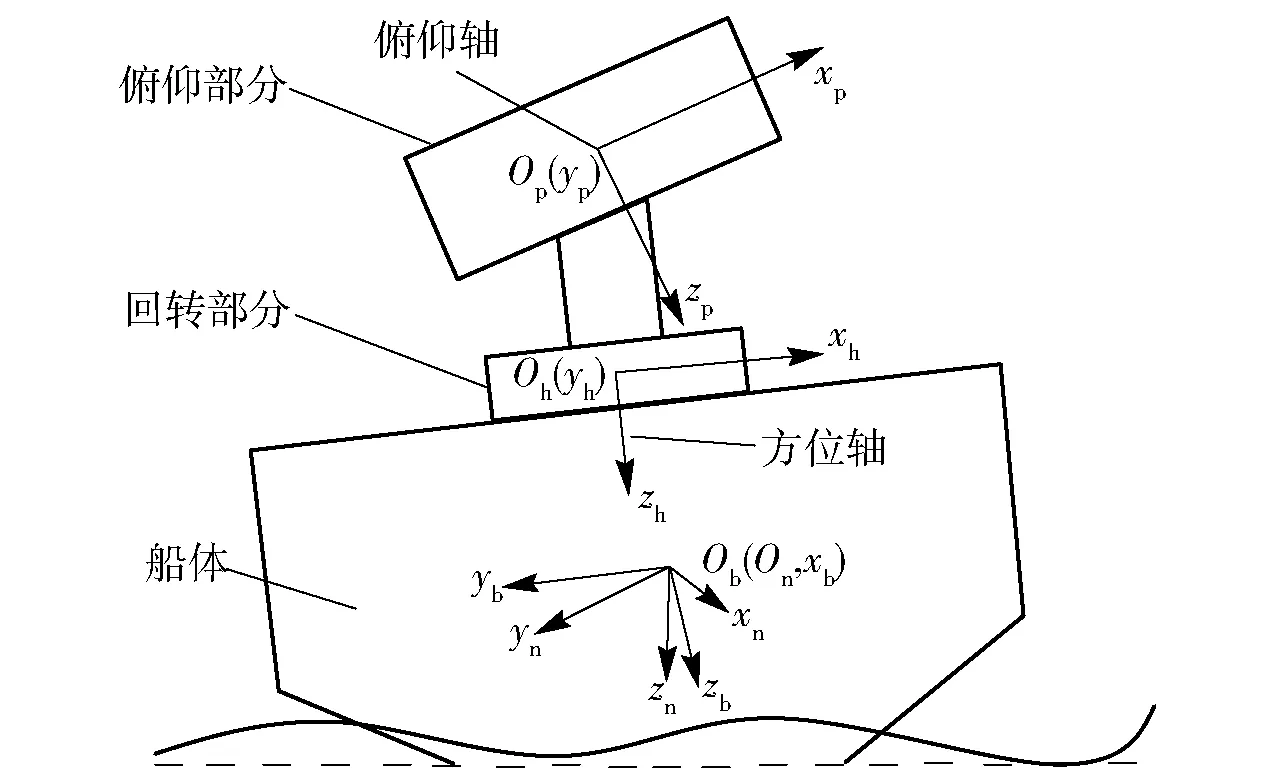
图1 STE随动系统结构及坐标示意图Fig.1 Structure and coordinate of STE servo system

2 运动学建模

2.1 坐标转换

2.1.1 从大地坐标系到船体坐标系的坐标转换

由船体纵滚、横摇、航向引起的坐标转换矩阵分别为

(1)

式中：φ、θ、ψ分别为船体在大地坐标系下的纵滚角、横摇角、偏航角。

在海中航行的舰船摇摆大致有随意摇摆、先纵滚后横摇、先横摇后纵滚3种。由于随意摇摆分析复杂，纵滚比横摇周期长、振幅短，为了分析简单且接近实际，采用先纵滚后横摇变换[15]。则从大地坐标系到船体坐标系的坐标转换矩阵Rn→b为

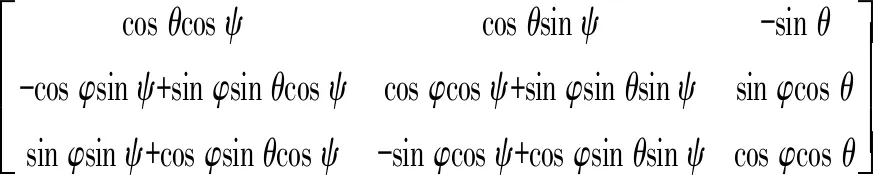
2.1.2 从船体坐标系到俯仰坐标系的坐标转换

船体坐标系经过转动一个方位角βb并平移(Δxβ,Δyβ,Δzβ)后，得到方位坐标系，因此齐次坐标转换矩阵[16]为

(2)

方位坐标系经过转动一个俯仰角εb并平移(Δxε,Δyε,Δzε)后，得到俯仰坐标系，因此齐次坐标转换矩阵为

(3)

由于Rb→h和Rh→p中的平移量对后面的运算没有影响，可以忽略。

2.2 运动学关系

2.2.1 方位角与俯仰角

大地坐标系下目标的球坐标为(D,εn,βn)，其中D为目标距坐标原点的距离，εn和βn分别为目标的俯仰角和方位角，转换为直角坐标为

(4)

则船体坐标系下的目标点坐标为

(5)

得到的随动方位角βb、俯仰角εb(二者都是目标在船体坐标系中的角度)分别为

(6)

(7)

由(5)式～(7)式可知， STE随动系统的方位角、俯仰角与目标点和发射点距离无关，这与文献[17]的结论一致。

2.2.2 角速度及其微分

转塔在大地坐标系下的角速度为

(8)

角速度的微分为

(9)

(10)

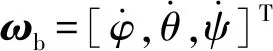
发射管在大地坐标系下的角速度为

(11)

角速度的微分为

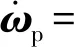
(12)

(13)

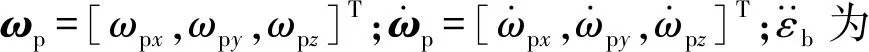
2.2.3 平动速度及其微分

方位坐标系原点在大地坐标系下的速度为

(14)

转塔质心在大地坐标系下的速度为

(15)

式中：u、v、w为船体在大地坐标系下的平动速度分量；xbh、ybh、zbh为方位坐标系原点在船体坐标系中的坐标分量；vhm为转塔质心在大地系下的速度；xhm、yhm、zhm为转塔质心在方位坐标系中的坐标分量。

同理，大地坐标系下发射管质心的速度为

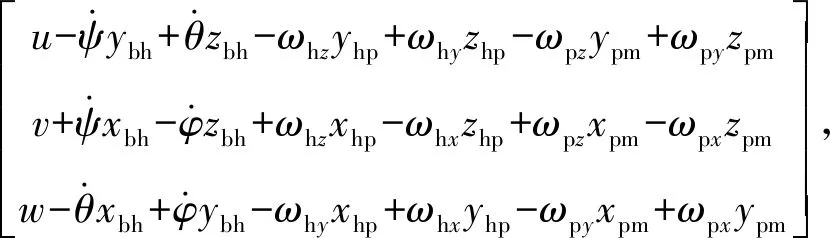
3 动力学建模

根据拉格朗日动力学方程[18-19]得

(16)

式中：Ek为系统动能；q为广义坐标；Q为广义主动力；j为广义坐标序号。

在STE随动系统中，广义坐标有两个，分别为βb和εb，广义主动力有重力G、运动阻力和作用于转塔和发射管的转矩，即

(17)

将(17)式代入(16)式中，得到STE随动系统的动力学模型为

(18)

式中：Ek=Ekhr+Ekht+Ekpr+Ekpt，Ekhr和Ekht分别为转塔的转动动能和平动动能，Ekpr和Ekpt分别为发射管的转动动能和平动动能；Tβ和Tε分别为转塔轴和发射管轴输入总力矩。

由(18)式可以看出，STE随动系统工作过程中受到回转部分、俯仰部分的重力势能、动能和不平衡力矩(∂Ep/∂βb、∂Ep/∂εb)等因素影响。随动控制过程复杂，干扰量众多。STE随动系统各个部分的重力势能、动能和不平衡力矩将在下文给出。

3.1 转塔动能及不平衡力矩计算

3.1.1 转塔动能

转塔平动动能、转动动能分别为

(19)

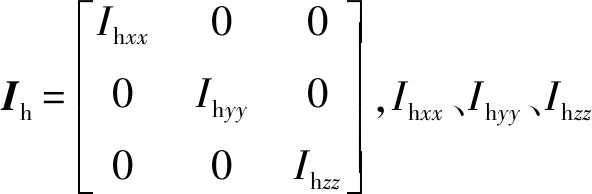
3.1.2 转塔不平衡力矩

转塔重心在大地坐标系的坐标为

(20)

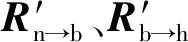
由(20)式得转塔重心高度为

zh=(-cosβbsinθ+sinβbsinφcosθ)xhm+ sinβbsinθyhm+cosβbsinφcosθyhm+ cosφcosθzhm+z0,

(21)

式中：z0为与β、ε无关的变量。

选大地坐标系下水平面为零势能面，得转塔重力势能为

Eph=mhgzh，

(22)

进一步推导得转塔关于两个广义坐标的不平衡力矩为

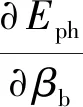
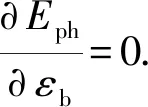
(23)

3.2 发射管动能及不平衡力矩计算

3.2.1 发射管动能

发射管平动动能、转动动能分别为

(24)

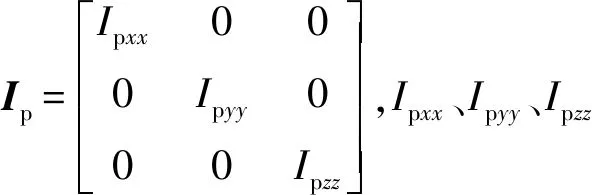
3.2.2 发射管不平衡力矩

发射管重心在大地坐标系中的坐标为

(25)

由(25)式可得发射管重心高度：

zp=sinβbsinφbcosθb(xhp+cosεbxpm+sinεbzpm)- cosβbsinθb(xhp+cosεbxpm+sinεbzpm)+

(sinβbsinθb+cosβbsinφbcosθb)(yhp+ypm)+ cosφbcosθb(zhp-sinεbxpm+cosεbzpm)+z1，

式中：z1为与β、ε无关的变量。选大地坐标系下水平面为零势能面，得发射管重力势能为

Epp=mpgzp，

(26)

进一步推导得发射管关于两个广义坐标的不平衡力矩为

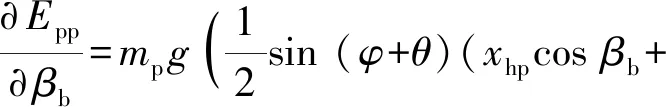
(27)

4 仿真分析

根据建立的动力学模型进行数值仿真分析，研究摇摆角和目标运动对随动过程中方位和俯仰力矩的影响。设STE随动系统的转轴与惯性主轴一致，则其惯量阵为对角阵。为了研究方便，将摇摆角近似为正弦规律变化。

STE随动系统机械参数为：Ihxx=4 000 kg·m2,Ihyy=3 400 kg·m2,Ihzz=5 000 kg·m2,Ipxx=180 kg·m2,Ipyy=860 kg·m2,Ipzz=750 kg·m2；mh=4 000 kg,mp=1 500 kg；xbh=ybh=0,zbh=1.0 m；xhp=yhp=0 m,zhp=1.0 m；xpm=0.5 m,ypm=zpm=0.5 m.

4.1 摇摆角对随动力矩的影响

4.1.1 幅值对力矩的影响

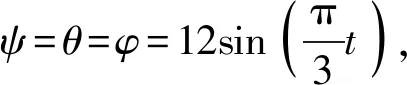
图2 不同幅值下的方位轴随动力矩Fig.2 Servo torques of azimuth axis at different swing angles

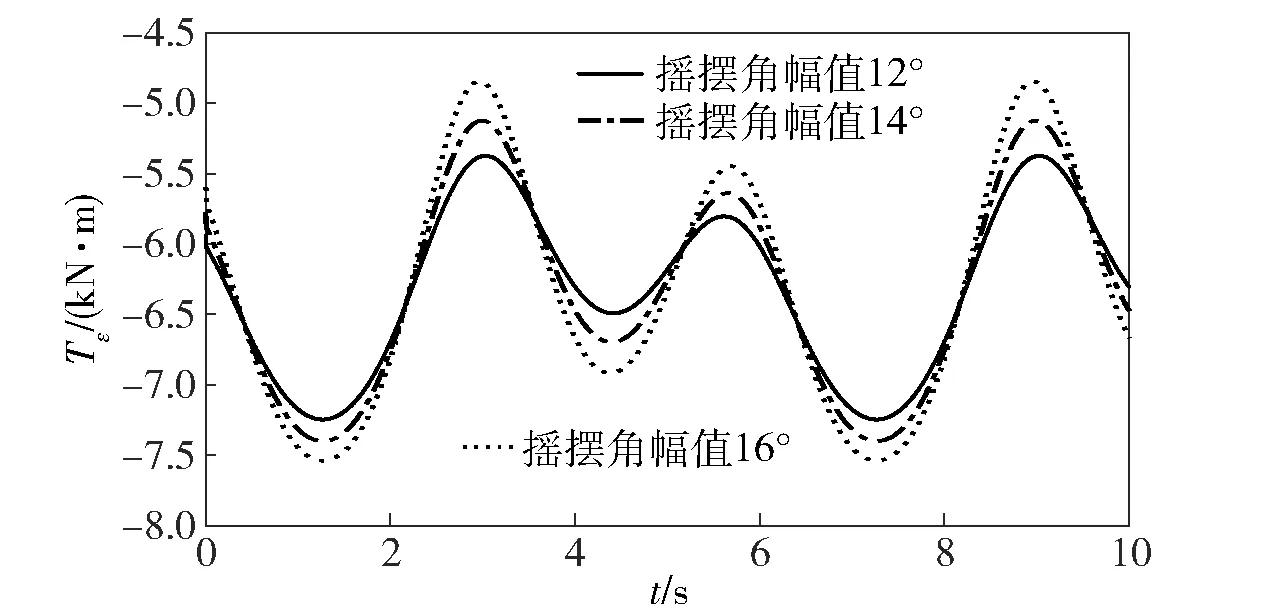
图3 不同幅值下的俯仰轴随动力矩Fig.3 Servo torques of elevation axis at different swing angles

4.1.2 周期对力矩的影响

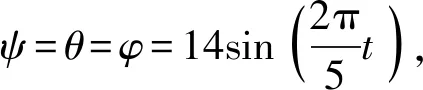
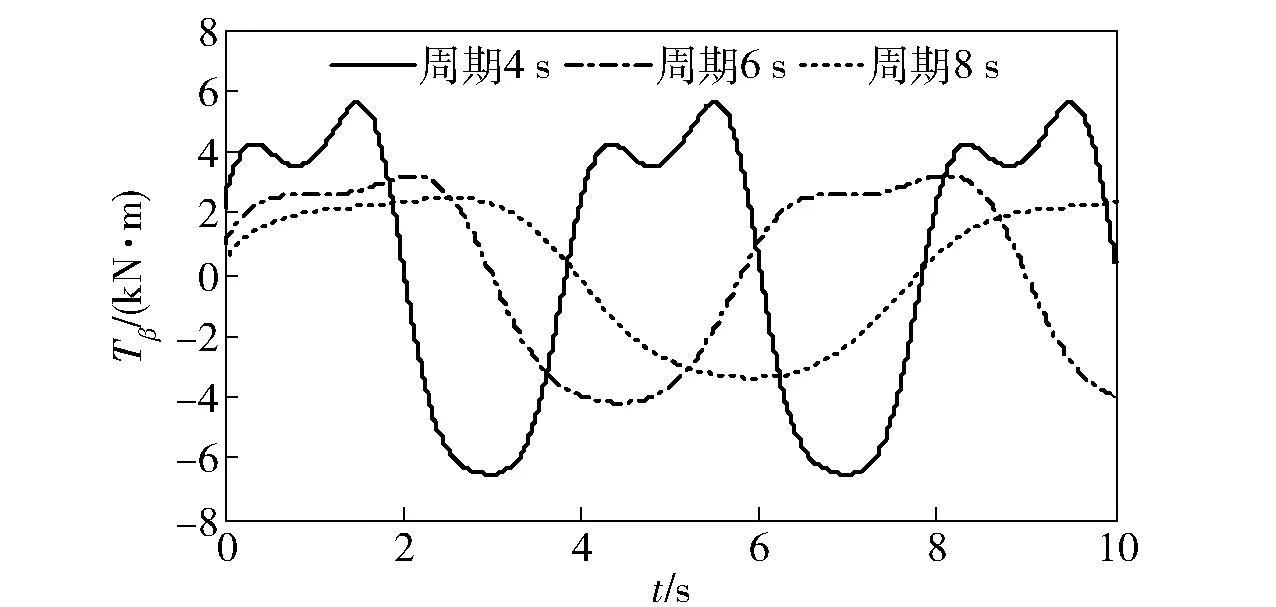
图4 不同周期下的方位轴随动力矩Fig.4 Servo torques of azimuth axis at different swing frequencies

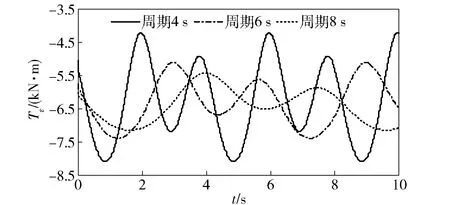
图5 不同周期下的俯仰轴随动力矩Fig.5 Servol torques of elevation axis at different swing frequencies

4.1.3 相位间隔对力矩的影响

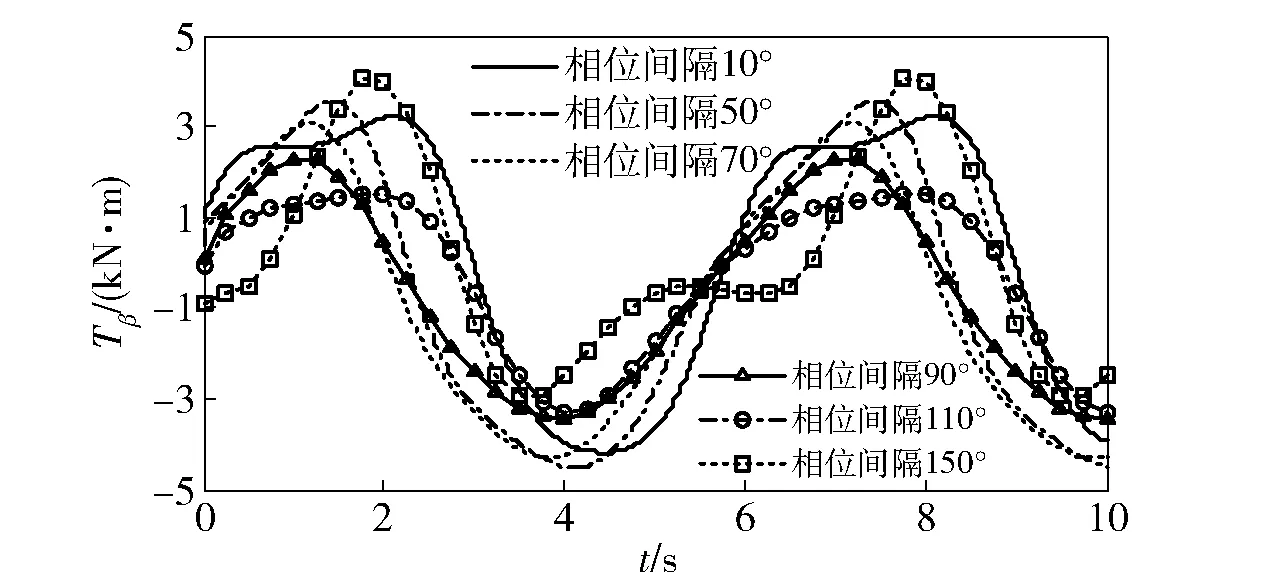
图6 不同相位间隔下的方位轴随动力矩Fig.6 Servo torques of azimuth axis under different phase differences

图7 不同相位间隔下的俯仰轴随动力矩Fig.7 Servo torques of elevation axis under different phase differences

综合上述3组仿真结果可知，摇摆角周期对随动力矩的影响效果最明显、幅值次之，相位间隔对随动影响最小；摇摆角变化对方位轴随动力矩的影响明显大于俯仰轴随动力矩。

4.2 目标运动状态对随动力矩的影响

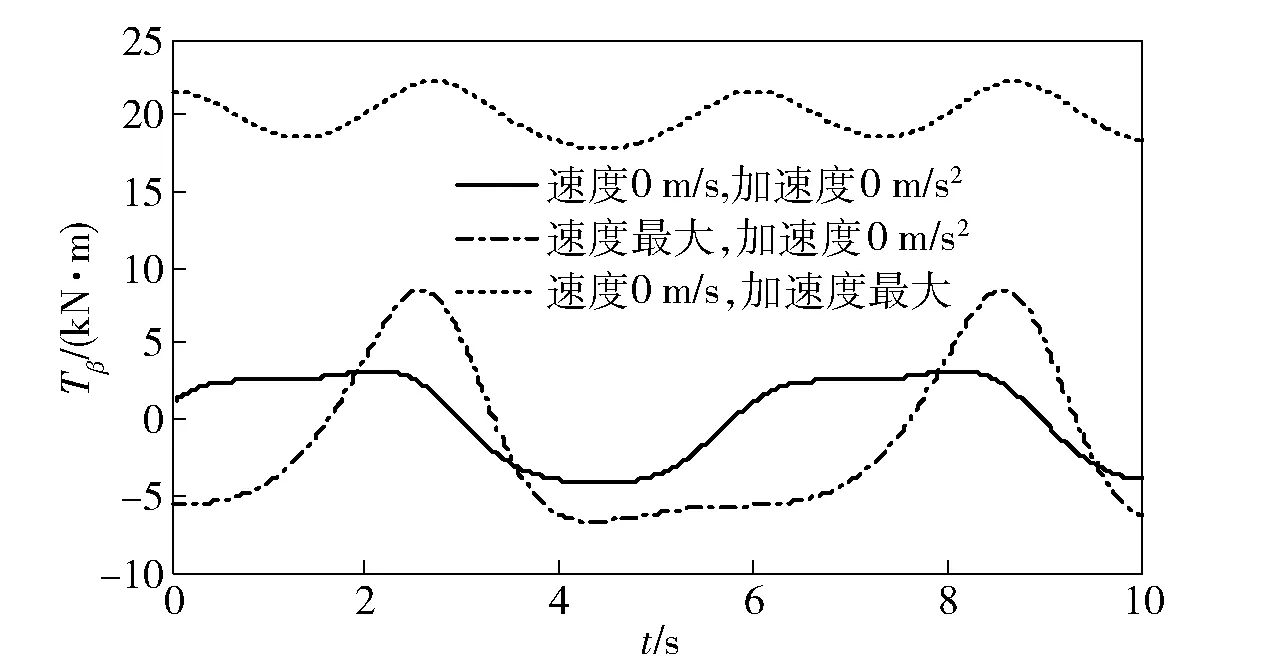
图8 不同目标运动状态下的方位轴随动力矩Fig.8 Servo torques of azimuth axis under different target moving states

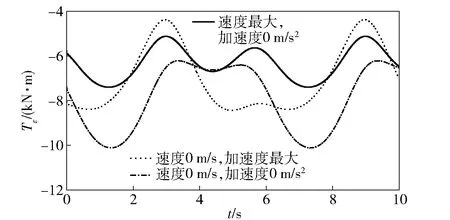
图9 不同目标运动状态下的俯仰轴随动力矩Fig.9 Servo torques of elevation axis under different target moving states

由图8和图9可知：目标以最大速度匀速运动时，方位轴随动力矩约增加60%，俯仰轴随动力矩约增加14%；目标以最大加速度运动时，方位轴随动力矩约增加300%，俯仰轴随动力矩约增加36%. 由此可得结论：目标运动会引起随动力矩的增大，且相对于俯仰轴随动力矩，目标运动对方位轴随动力矩的影响更为明显；相对于目标速度，目标加速度对随动力矩的影响效果更加明显。

5 结论

本文对STE随动系统各部分进行了坐标系的定义，在此基础上，建立了二轴随动系统的拉格朗日动力学模型，并结合STE的结构参数，对随动控制系统进行了动力学数值仿真，定量研究了摇摆角和目标运动对方位轴和俯仰轴随动力矩的影响。根据仿真结果得出以下主要结论：

1)摇摆角周期对方位轴和俯仰轴随动力矩的影响最为明显，幅值次之，相位间隔对随动影响最小。摇摆角幅值增大或周期的减小，会引起方位轴和俯仰轴随动力矩同时增大。

2)摇摆角相位间隔对随动力矩影响比较复杂，在不同区间内，相位间隔变化对随动力矩的影响效果不同。

3)相对于速度，目标的加速度对随动力矩的影响更为明显。

4) 本文所建模型和仿真结果为STE随动系统的设计和分析提供了理论基础，对其他随动系统的研究也具有重要意义。