内弹道两相流三维并行数值模拟

程诚，张小兵

(南京理工大学 能源与动力工程学院, 江苏 南京 210094)

0 引言

随着信息化弹药和新概念发射技术的飞速发展，对于内弹道发射性能、可靠性和安全性水平提出了更高要求，传统数值模拟手段已不能完全满足人们对于深入分析内弹道性能的迫切需求，因此更加贴切实际、结果更为准确的内弹道两相流数值模拟已经成为内弹道领域的重要发展方向之一。

内弹道两相流数值模拟作为火炮装药设计、发射安全性等研究的重要手段，已经形成了从一维、二维到三维的理论模型体系[1-2]。在内弹道两相流数值模拟的实际应用中，受制于计算成本及两相流编码复杂性等问题，近年来仍主要以一维和部分二维计算为主，将膛内的装药结构简化为轴对称或准轴对称模型，如：Nussbaum等[3]研究了一维和二维点火模型对内弹道性能的影响，Miura等[4]利用二维轴对称内弹道模型研究了不同底火结构对内弹道性能的影响，Georgi等[5]用二维内弹道研究点火区域，点火完成后采用一维内弹道代码进行计算，以提高计算效率,Woodley等[6]采二维内弹道模型研究了烟火药剂的点火与燃烧特性。然而一维或二维模型在解决一些膛内非对称装药及点传火等问题时，与膛内实际多相燃烧与流动过程还有较大误差，亟需开展三维模拟研究。

目前内弹道三维两相流数值模拟国外主要以美国开发的ARL-NGEN3代码为代表[7-8]。另外，Miura等[9]对膛内点传火过程进行了三维数值仿真研究，Jang等[10]也开展了内弹道三维两相流数值模拟的探索研究。国内刘千里等[11]和翁春生等[12]先后开展了点火管非对称点传火过程的三维两相流数值模拟应用。总体来说国内三维内弹道两相流数值模拟的应用研究较少，这主要是由于数值计算每增加一维，计算工作量将增加多个量级，特别是内弹道两相流模拟需要大量的辅助方程，因此，亟需提高三维两相流数值模拟的计算效率，降低计算成本。

2.新时代上海市住房金融风险概率评估。综合上述上海市房地产风险指数、住房市场杠杆率、泡沫指数测度与预测结果，笔者判断，新时代上海市住房金融风险，在乐观预测情景下，早在 2014年就已经进入低风险区间，2039年进入安全区间；在中性预测情景下，将于 2028年进入高风险区；在悲观预测情景下，将于2021年进入高风险区。

本文在二维数值模拟方法研究的基础上[13-15]，基于任意拉格朗日-欧拉(ALE)方法建立了火炮内弹道三维两相流模型，并结合MPI分区并行算法，解决了内弹道两相流三维数值模拟的计算工作量问题，为内弹道两相流三维仿真的实际应用提供参考。

1 三维内弹道气固两相流矢通量守恒方程组

为了简化内弹道数值模拟的复杂性，需对实际物理过程进行适当假设，主要包括：

1) 采用双流体模型，将发射药颗粒群作为具有连续介质特性的拟流体来处理；

为了减少网格引起的误差，保证计算精度及稳定性，计算区域采用六面体结构化网格系统。弹底网格运动采用内弹道计算中常用的动网格技术[1,14]，弹底网格层高度随着弹丸运动不断增加，当弹底网格层高度大于给定值时，沿弹丸运动方向的弹底区域新增加一层网格，新增网格的各通量可用2阶精度插值求得。弹丸运动速度即运动边界速度，可根据如下弹丸运动方程求得：

图3为弹丸运动前不同时刻的膛内压力分布云图。从图3中可以看出，在内弹道初始阶段，无论是径向方向还是轴向方向，膛内都呈现出明显的多维效应，尤其是在点火区域。随着膛内火药燃气的不断被点燃，膛内压力由膛底向弹底方向传递，并不断上升。随着膛内点火过程的逐步完成，膛内径向的多维效应逐渐减弱，而轴向方向依然存在从膛底到弹底方向的明显压力梯度。

毋庸置疑，蓝洞的得名归功于其壮观的蓝色海水，它也是扎金索斯岛最有名的自然景观之一。其中一些洞穴只能乘船参观，而其他洞穴只有专业的游泳者和潜水员才能够进入。

4) 火药颗粒服从几何燃烧和指数燃烧定律；

5) 气相状态方程采用Nobel-Abel状态方程；

在《书·周官》有云：“立太师、太傅、太保，兹惟三公，论道经邦，变理阴阳，官不必备，惟其人。”太师与太傅、太保合称三公，指的是在朝中共同负责军政的最高长官。少师与少傅、少保合称三少，是辅导太子的官员。师与狮谐音，因为常常将狮子作为吉祥图案绘制于瓷器之上，将一对狮子和如意配合在一起寓意“事事（狮狮）如意”；将一只大狮配一只小狮寓意“太师少师（太狮少狮）”；五头狮子在一起寓意“五子登科”；狮子和瓶结合在一起，寓意“事事平安”；狮子滚绣球表示财源不断、子嗣昌盛等。

6) 点火区域及点火管内考虑多维效应，通过质量、动量及能量方程与药室内守恒方程进行耦合。

以ALE方法[16-17]对无黏流动的三维内弹道气固两相流守恒方程进行重建。由于弹丸仅沿身管轴线方向运动，故以下内弹道两相流守恒方程组只考虑了x方向的网格运动。

(1)

式中：

(2)

φ为空隙率，ρg为气相密度，ρp为固相密度，ug、vg、wg分别为x方向、y方向、z方向的气相速度，up、vp、wp分别为x方向、y方向、z方向的固相速度，Eg为气相总能；

它发表于1899年，以发现者乔治亚历山大·皮克的名字命名而得名.主要解决格点多边形的面积问题：若S为多边形面积，L是边界上的格点数，N是内部格点数，则有

(3)

图7为不同点火管长度下的膛内压力波变化曲线。图8为弹丸初速vd、第1个压力波负幅值Δp、最大膛压pmax随点火管长度的变化关系。从图7和图8中可以看出，随着点火管长度的增加，提高了点火区域的长度，保证了膛内装药能够迅速着火，且点火分布也更加均匀，因此膛内压力波随之降低，同时弹丸初速与最大膛压均随之增加。

(4)

(5)

(6)

图4为弹丸开始运动后不同时刻的膛内压力分布云图。从图4可以看出，膛内径向方向的多维效应已经基本消失，膛内主要是沿轴向方向的压力梯度分布。随着膛底压力不断向弹底传递，同时膛底火药颗粒的不断燃烧，在t=3.0 ms时刻弹底压力大于膛底压力，从弹底向膛底方向呈现出压力梯度分布，从而会出现负向压力波。在t=5.0 ms时刻膛底压力又比弹底压力大，轴向方向的压力梯度分布又变为从膛底向弹底方向。随着火药燃气的不断释放，膛内压力仍然在不断上升，如t=7.0 ms时刻所示。随着弹丸的不断运动以及膛内火药燃气逐渐燃完，膛内压力开始出现下降，但依然保持从膛底向弹底方向的压力梯度分布，如t=9.0 ms时刻所示。

2 数值并行计算方法

通过时间分裂法进行三维控制体求解，其中对流项采用高阶MUSCL格式进行离散，时间方向的常微分方程采用4阶龙格库塔法进行计算[18]。弹丸未运动前，气固相在膛内所有壁面处均采用静止固壁边界条件。当弹丸开始运动后，气固相在弹底采用固壁运动边界条件[14]。

2) 假设发射药颗粒不可压缩，则按体积计算的固相平均温度不受运动的影响，因此固相宏观能量方程可由热传导方程所代替，故忽略固相能量方程；

(7)

式中：A为身管截面积；pd为弹底压力；φ1为次要功计算系数；vd为弹丸速度。

计算区域通过MPI并行方法[19]进行分区，如图1所示。MPI主进程将初始条件及网格信息通过消息传递分配到每个子进程及所对应内存中，每个子区域分别在不同进程上进行计算。由于采用2阶差分格式，因此当子区域边界类型为相邻内边界时，需要用到相邻分区的流场信息，因此子区域内需建立虚拟网格，主进程将相邻子区域的边界数据传递给本区域的虚拟网格，从而实现子区域的边界计算。

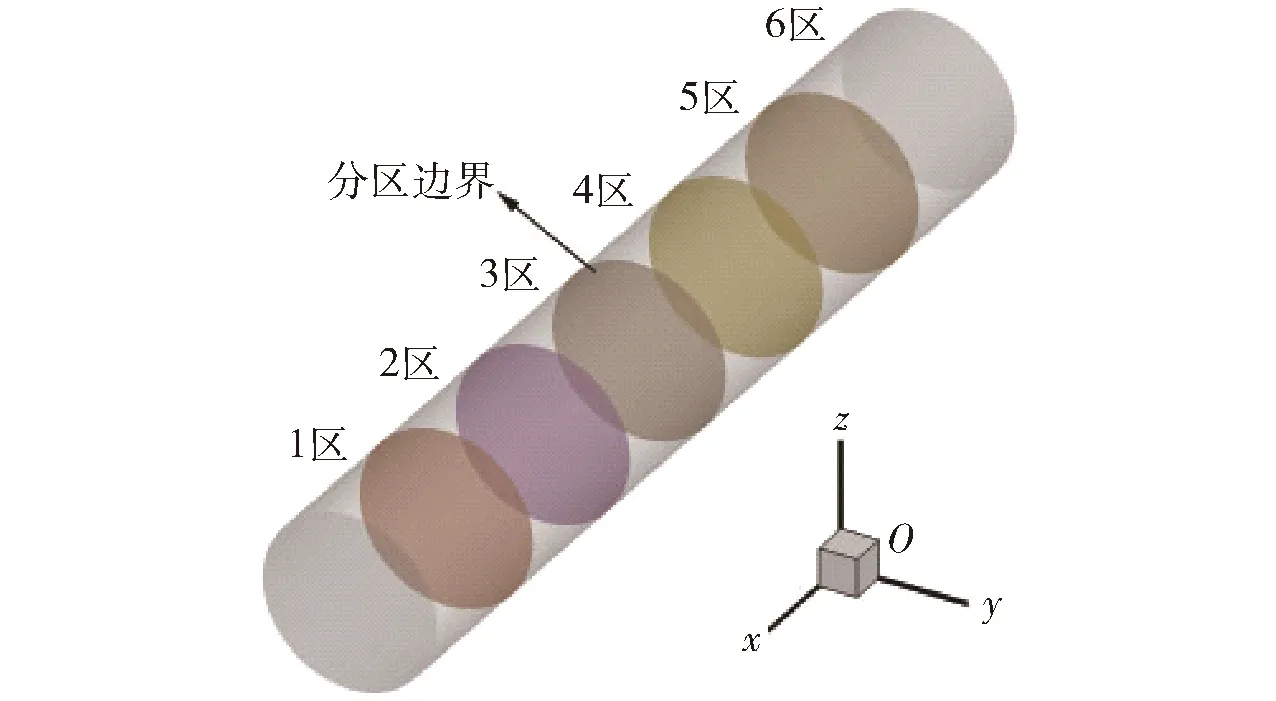
图1 计算区域分区示意图Fig.1 Partition of computational domain

随着弹底新增网格数量的不断增加，与其他子区域之间的网格数目差异越来越大，导致子区域计算负载出现不平衡，因此每运行一定时间步数后，根据当前网格总数及所调用进程数，重新对网格进行平均分区，以保证各子区域之间的计算负载平衡。同时由于弹丸仅在身管轴线方向发生一维运动，为了方便相邻分区边界数据的传递以及减少数据通讯量，分区网格区域的动态调整仅在弹丸运动方向进行。

3 结果与分析

为了验证所发展的内弹道三维两相流并行计算方法的准确性和并行效率，本文以某132 mm火炮中心点火装药结构的内弹道两相流动过程为对象，分别开展了三维仿真结果验证、点传火性能以及并行性能分析研究。仿真验证中所使用内弹道计算主要参数有：弹重45.36 kg，弹丸全行程长4.32 m，装药量为9.53 kg，药室容积 0.01 m3，点火药量0.226 8 kg.

3.1 仿真结果验证

为了说明三维内弹道两相流数值模拟的可靠性，首先将三维计算结果与文献[20]中不同代码(IBHVG2、XKTC、FHIBS、AMI)结果进行比对；然后对计算获得的三维结果与二维结果进行对比，进一步验证本数值仿真结果的一致性。表1为最大膛压、最大弹底压力、弹丸初速的仿真结果与文献[20]结果对比。从表1中可以看出本文的三维计算结果在文献[20]结果范围内，与文献[20]结果所示的不同代码结果吻合较好。由于不同代码在颗粒间应力、相间阻力等辅助方程使用上有一定差异，造成了不同代码间的计算结果有一定差别。图2为弹丸速度、行程随时间变化曲线。从图2中可以看出，三维与二维计算结果在不同时刻下虽有一定的差别，但总体上三维和二维计算结果曲线吻合都较好，说明了本文内弹道两相流三维与二维计算结果有较好的一致性。

表1 三维计算结果与文献[20]结果对比Tab.1 Comparison of the simulated three-and two-dimensional results and the results in Ref.[20]

图2 三维与二维仿真的内弹道特性对比Fig.2 Comparison of three-and two-dimensional interior ballistic performances

3.2 三维数值计算结果

图3 弹丸运动前膛内压力分布Fig.3 Contours of in-bore pressures at different times before projectile moving

3) 不考虑气相与固相间黏性作用，不考虑湍流影响；

3.5.2 拔管时机 对于泌尿系统手术的患者，推荐在夜间拔除导尿管(B级推荐)［5］。多项研究表明，与早晨(6:00～8:00)相比，夜间(22:00～0:00)拔除导尿管有利于增加患者导尿管拔出后的第1次排尿量，且缩短了患者从拔管到第1次排尿之间的时间间隔。

图4 弹丸运动后膛内压力分布Fig.4 Contours of in-bore pressures at different times after projectile moving

画图、读图，看图表达、语言翻译成图；从复杂的图形中找出所需要的图形，从函数图象中找出或者想象出函数的基本性质以及方程的性质。

图5 膛内气相速度分布Fig.5 Contours of in-bore gas velocity at different times

图5为不同时刻膛内气相速度分布图。图6为1/2点火管长度处r=22 mm圆周上的气相速度分布曲线。由图5和图6可知，膛内点火区域的多维效应最为明显，即使弹丸开始运动后，在点火区域仍然存在一定的多维效应。随着弹丸不断运动及点火过程的结束，该多维效应不断减弱。结合图3(c)所示压力分布云图，t=1.0 ms时膛底与弹底之间存在强压差，因此膛内气体由膛底向弹底不断运动，而且点火区域的火药燃气也不断向膛壁方向传递，但此时该多维强气流还未传播到弹底，如图5(a)所示。当t=2.0 ms时，膛内的多维传播仍然在向弹底运动，且强火药燃气流已经接近弹底，如图5(b)所示。当t=3.0 ms时，如图5(c)所示，随着弹底区域火药的燃烧及压力波在弹底的反射，弹底气流开始向膛底方向运动，且与膛底气流在膛内中间区域相遇，造成中间区域的气流速度明显下降。随着弹丸的逐渐运动以及膛内发射药的不断燃烧，结合图4(b)中的压力分布图，t=5.0 ms时膛内气流速度主要为从膛底向弹底方向的轴向速度，仅在点火区域附近出现多维效应，且强度明显衰减，如图5(d)所示。同时由于膛内的压力梯度也在减弱，因此膛内气流合速度小于点火初期时的气流速度。结合图5(c)和图5(d)可以看出，随着弹丸的不断加速，总体气流速度还是在不断增加。

图6 1/2点火管长度处r=22 mm圆周上的气相速度分布曲线Fig.6 Gas velocity distributions on the circumferences at half length of igniter for r=22 mm

3.3 不同点火管参数对内弹道性能的影响

通过以上内弹道两相流三维数值模拟结果可知，点火阶段的三维现象最为明显，同时点火性能的好坏又直接影响着发射安全性等关键的内弹道指标。已有研究表明[21]，合理的点火管长度和直径可以有效地改善点火性能以及减小膛内压力波危害，下面通过研究不同点火管长度和直径对内弹道性能的影响，进一步验证本文三维数值研究工具的可靠性。

um为动边界速度，p为气相压力，Rp为颗粒间应力；

对于如何创新基层社会管理模式，学者们从不同角度提出了不同的社会管理模式。如李文祥提出政府、企业、社区和大学的“四方共建”模式；[3]赵树凯提出政府与民间力量的“多中心治理”乡村治理范式；[1]卢芳霞的“枫桥经验”[4]等。从社会管理研究和实际运作来看，社会管理具有两个基本点，即以管控群体冲突、实现社会和谐为目标，以发展民众生机、增进社会福利为基础，[3]其管理方式依赖于综合运用行政手段、法律手段、经济手段、政策手段和科技手段。

图7 不同点火管长度时压力波曲线Fig.7 Pressure wave curves for different lengths of igniter

图8 点火管长度对内弹道特性参数的影响Fig.8 Effect of igniter length on interior ballistic characteristics

点火管直径是影响点火性能的重要因素之一。图9为不同点火管直径下的膛内压力波变化曲线。图10为弹丸初速vd、第1个压力波负幅值Δp、最大膛压pmax随点火管直径的变化关系。从图9和图10中可以看出，点火管直径过大或过小都将引起最大膛压及第一负向压力波幅值的增加。点火管直径过小，造成局部区域的点火激励增强，与底部点火类似，会形成较大的压力梯度。点火管直径过大，在点火管与药室内壁之间的径向方向会造成强烈的点火激励与颗粒堆积，从而引起强压力波动。因此，合理设计点火管直径有利于抑制膛内压力波。

图9 不同点火管直径时压力波曲线Fig.9 Pressure wave curves for different diameters of igniter

图10 点火管直径对内弹道特性参数的影响Fig.10 Effect of igniter diameter on interior ballistic characteristics

3.4 并行性能分析

并行计算中除了计算结果的准确性，加速比和并行效率等也是衡量并行计算性能的主要指标。加速比为串行算法与并行算法计算相同任务时的耗时比值，并行效率为加速比与计算所用进程个数的比值。表2 给出了不同进程数与运行时间、加速比、并行效率、并行成本之间的关系，其中运行时间以运行1 500步为基本统计单位。从表2可以看出，随着进程数的增加，加速比也不断增加。并行效率随着进程数的增加会不断下降，但并行效率仍较为可观。这主要是因为随着并行数的增加，并行分区之间的网格通讯量随之增加，主进程需要处理的数据量就会增多，从而导致并行处理所引起的额外开销增加，因此在进行并行进程选择时需要综合考虑网格数量及额外开销耗时等因素。

表2 并行效率对比Tab.2 Comparison of parallel efficiencies

4 结论

本文基于任意拉格朗日方法，建立了内弹道两相流三维数学模型，同时结合MPI分区并行算法，对三维计算网格进行多核分区计算，数值模拟了内弹道三维两相流动过程。主要结论如下：

1) 内弹道点火阶段多维效应明显，随着发射药不断燃烧及弹丸运动，多维效应逐渐减弱。

二是通过应用服务器对数据库服务器中存储的各传感器数据从多个维度进行分析,将数据进行处理分析并展现到互联网上、微信等手机APP。

2) 三维数值模拟结果与文献[20]结果吻合较好，说明了所构造内弹道两相流三维模型及并行程序的准确性，同时与二维结果也有较好的一致性。

3) 研究了不同点火管长度及管径对内弹道性能的影响，进一步验证了本文内弹道两相流三维数值研究工具的可靠性，同时也为后续深入开展多维点火性能的优化研究提供了基础。

在太湖流域水环境综合整治方面，市政府批复的《上海市太湖流域水环境综合治理实施方案》设定治理项目总计30个（不含科技支撑项目），总计划投资31.68亿元。青浦区还深入推进第四轮环保三年行动计划水环境治理，共计23项工作，总投资21.12亿元。这两项行动涉及饮用水安全、污水（泥）整治、河道整治、农村污染治理、点源污染治理、农村面源污染治理等6个方面。目前太湖流域水环境综合治理近期项目已经完成，进入中期评估阶段。

4) 数值实验验证了本文所发展的内弹道两相流三维并行方法具有较高的并行效率，较大幅度地提高了三维计算的速度，为内弹道三维两相流数值模拟研究的实际应用提供了新的研究工具。