六足机器人不规则地形下的运动规划算法研究

(1.天津商业大学 机械工程学院，天津 300134； 2.北京理工大学 机电学院，北京 100081)

0 引言

与轮式或履带式机器人相比，足式机器人的落足点是离散的，因而足式机器人能在足尖点可达域范围内灵活调整行走姿态，并合理选择支撑点，具有更强的不规则地形适应能力。但如何才能为足式机器人设计出可适应不规则地形环境的步行控制系统，成为足式机器人研发过程中面临的最大挑战[1-2]。众所周知，自然界中的各种生物通过物竞天择和长期进化，已对外界环境产生了极强的适应性，在能量转换、运动控制、姿态调节、信息处理和方位辨别等方面还表现出了高度的合理性，已日益成为人类开发先进技术装备的参照物。为了研制出合适的足式机器人步行控制系统，国内外的机器人学专家们正密切关注仿生设计，力图从动物适应不规则地形的突出能力中寻找灵感与方法[3]。昆虫具有良好的运动和环境适应能力，是足式机器人理想的仿生对象，大部分的六足机器人均采用了蚂蚁等昆虫的结构形式[4-6]。除了在结构方式外,模仿动物的运动控制方式也是重要的仿生研究内容。通过对昆虫神经系统的研究，基于中枢模式发生(CPG)开始广泛应用于足式机器人的节律运动控制之中[7-9]。已经提出的CPG网络均具有较强的耦合性，当足式机器人在不规则地形下运动时，由于参数整定的困难，运动效果较差[10]。通过观察动物的运动来获得运动控制灵感是一种简单有效的仿生手段，文献[11]通过对蚂蚁的观察实验提出了一种转向运动偏差的修正算法，提供了六足机器人转向运动的稳定性。本文将采用类似的方法，通过对蚂蚁运动的观察实验，提出一种六足机器人在不规则地形下的运动控制算法，并通过样机试验对所提算法进行验证。

1 蚂蚁运动观测实验与分析

作为昆虫纲的典型物种，蚂蚁的运动能力极其优秀，具有很高的仿生研究价值，而其躯、腿分明的体型特点亦使深入观测其运动特征较为方便。本文采用与文献[11]类似的实验思路、仪器、环境和方法，重点模拟了两种障碍物情况(平放障碍柱及堆叠障碍柱)，通过观察蚂蚁经过这两种理想、典型的障碍物时的姿态特征，寻找蚂蚁在不规则地形环境中的运动应重点模拟了两种障碍物情况(平放障碍柱及堆叠障碍柱)，通过观察蚂蚁经过这两种理想、典型的障碍物时的姿态特征，寻找蚂蚁在不规则地形环境中的运动应变策略。选取样本蚁的运动截图如图1所示。

图1 蚂蚁跨越障碍柱和障碍柱堆过程截图

由上述典型样本可以发现，蚂蚁在应对两种障碍时采取了不同的运动策略：当面对高度小于其躯体离地高度的障碍柱时，蚂蚁始终保持躯体与地面平行，没有出现侧倾、俯仰或翻转现象，与文献介绍的蚂蚁在理想环境下运动的姿态类似；而当面对高度大于其躯体离地高度的障碍柱堆时，蚂蚁则调整位姿以保持躯体与障碍物斜面平行。经过进一步的实验观察发现，几乎在任何时刻，蚂蚁躯体都平行于支撑相核心三足所确定的平面(蚂蚁可能会有超过三只足处于支撑相，而此处的“核心”三足是指处于躯体一侧的前足、后足以及对侧的中足)。

2 仿生六足机器人的运动学模型

图2所示为普通18关节六足机器人的机构简图。在任意腿着地情况下该机器人都具有6个自由度。在通常的运动学建模过程中，一般通过D-H方法为机器人的单腿建立三自由度的D-H模型，然后根据支撑相或摆动相的相位情况分别讨论机器人整体的运动学模型。该方法固然可以建立机器人的精确模型，但也存在明显缺点：首先是运动学模型较为复杂，不便于计算机程序编写；其次是将机器人的六足严格划分为一半属于支撑相和一半属于摆动相，忽视了六足中分别处于支撑相和摆动相的腿数并非完全相等的事实；最后是在探讨机器人支撑相腿时将机器人机构系统视为并联系统，在进行相应运动学解算时需对非线性方程组进行繁琐求解(而一旦超过三足着地则为冗余方程，求解更为困难)，而求解非线性方程组正是计算机的弱项，所以该模型在计算机上的复用性较差。

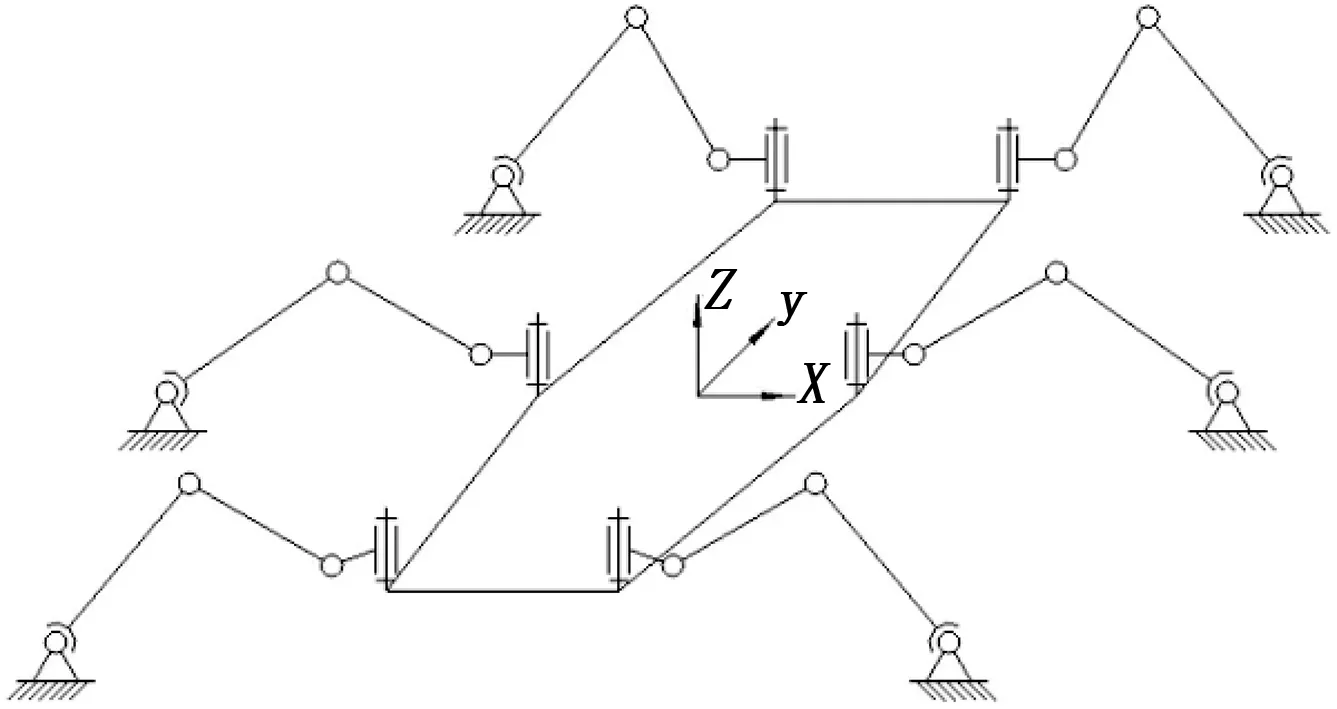
图2 六足机器人机构图

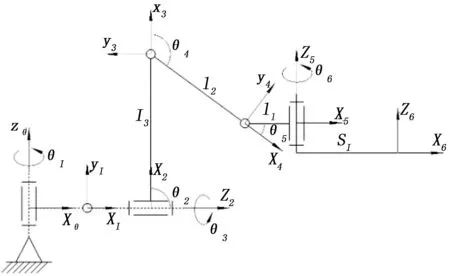
图3 六足机器人单腿D-H模型图

针对以上问题，本文提出建立D-H模型的另一种思路，即将地面与足端的球铰副反映到机器人的单腿D-H模型中，球铰副所代表的3自由度(在后文被称为被动关节)与机器人腿部3驱动关节(在后文被称为主动关节)正好分为两部分，不仅便于运动学模型解算，而且对于不需计算被动关节的情况可以不予计算，从而更符合接触点地形复杂的现实情况。六足机器人单腿模型只涉及地面、足端与躯体重心这三部分(该模型不需要区分支撑相与摆动相，将摆动相足端视为虚拟着地)，根据单腿模型6自由度即可确定机器人躯体位姿，根据躯体位姿又可确定机器人其他腿的位姿，这时可将并联系统理解成串连系统，从而大大降低了非线性方程组的求解难度。另外，整个系统几乎可以浓缩为单腿模型，并且各腿的模型完全相同，可以复用，这样不仅简化了系统的运动学模型，而且便于计算机编程以实现六足机器人的在线运动控制。

按照上述思路，建立六足机器人单腿D-H模型如图3所示，D-H参数见表1，图中虚线代表的构件长度为零，所有虚线构件代表地面与足端接触的球铰副。根据上述参数可以方便地获得:

(1)

由全局坐标系{G}与各足足端着地点坐标系的固定关系可得0GTi，再由躯体坐标系{B}(坐标系方向如图4所示)与各足的D-H模型中{6}的固定关系可得BGTi，从而可以方便地求解机器人躯体位姿与各主动自由度的关系。

表1 机器人单足D-H参数一览表

应当指出，机器人腿部必需两种传感器：一是位置传感器，用来感知各主动关节的运动位置；二是足端的力传感器，用来感知腿与地面的接触力。位置传感器可以保证腿准确地按规划运动，而力传感器可以保证足端很好地适应陌生地形。

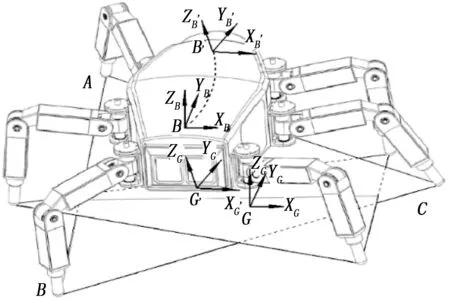
图4 六足机器人中的坐标系

3 仿生六足机器人运动规划算法研究

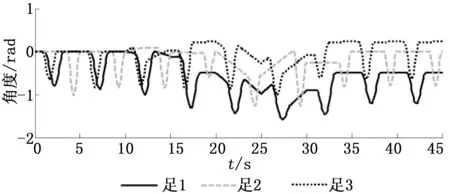
仿生六足机器人在任何时候都拥有六自由度，这意味着该机器人在运动中的位姿有多种选择，其足的运动位姿也有多种选择(理论上是无数种解)，而理想情况下机器人需要且只需要一种“解”，以期获得高效执行。另外，哪种运动策略更高效、更节能、更稳定，也是一个需要深入探讨的问题。而蚂蚁应对不规则地形的运动规律为仿生六足机器人在不规则地形条件下的运动提供了很好的规划方法。首先可以将六足机器人的运动地形划分为两种情况：浅度不平地形(H>h，其中H为机器人离地高度，h为地面不平幅度)和深度不平地形(H

3.1 浅度不平地形上的运动策略

当六足机器人在浅度不平地形上运动时，可建立初始状态下机器人与躯体坐标系{B}方向相同但原点不同的全局坐标系{G}，使得{B}原点在{G}上投影即为{G}原点。根据躯体重心坐标pB以及躯体绕{G}x,y,z轴旋转角度α,β,γ可获得BGTi，将蚂蚁应对障碍柱的运动规律转化为数学语言，即:

pBz(t)≡H,α(t)≡β(t)≡0

(2)

式中,pBz代表pB的z轴向分量。

由上式可知，通过pBx(t),pBy(t),γ(t)可确定唯一一条机器人躯体运动轨迹，该轨迹可保证机器人运动过程没有高度起伏、倾侧或俯仰现象出现。

在获知机器人躯体重心运动轨迹之后，即可按文献[13]所述方法规划机器人足端运动轨迹，根据前述D-H模型可获得机器人相应的关节运动轨迹。对于浅度不平地形，足端与未知地面的适应是一个难点，文献[14]所述二次规划以进行避障的方法以及机器人腿部力传感器的现实保证能很好地解决这一难题。当一次规划轨迹完成后，若机器人足端仍未感应到合适的着地点，则继续规划运动直至力传感器感知到合适的着地点，同时通过位置传感器获得的位置以及相应时刻的机器人位姿，确定相应足的着地点在{G}中的坐标，以便进行下一步运动规划。

3.2 深度不平地形上的运动策略

六足机器人在深度不平地形中的运动更为复杂，不仅机器人足部要适应未知地形，而且躯体位姿也要随地形的变化而变化。通过研究发现，不论六足昆虫采用何种步态，为了保证稳定性，六足每隔半个周期会同时着地，之后摆动相的核心三足陆续切向支撑相以支撑躯体稳定移动，而支撑相的核心三足陆续切向摆动相以探测新的着地点。借鉴这一特点，针对六足机器人不采用一成不变的全局坐标系，而是每隔半个运动周期即进行一次坐标系迭代。在机器人六足同时着地时刻，由支撑相即将切向摆动相的核心三足来确定全局坐标系{G}，那么各足位置在{G}坐标系下均为已知；然后以摆动相即将切向支撑相的核心三足着地点A,B,C构造新的全局坐标系{G’}，根据前述蚂蚁在应对障碍柱堆时的运动规律确定{G’}的构造条件：①{G’}的原点为△ABC重心；②{G’}z轴垂直于△ABC；③{G’}y轴与{G}yoz平面夹角反应机器人运动状况(直线前进时该夹角为零，转向时该夹角为相应角度)。根据条件①有：

(3)

式中,GpA,GpB,GpC,GpG'分别代表点A,B,C,G′在{G}中矢量坐标。

根据条件②有：

(4)

其中:

A=(GpCy-GpBy)(GpAz-GpBz)-(GpCz-GpBz)(GpAy-GpBy)

B=(GpCz-GpBz)(GpAx-GpBx)-(GpAz-GpBz)(GpCx-GpBx)

C= (GpAy-GpBy)(GpCx-GpBx)-(GpCy-GpBy)(GpAx-GpBx)

完成全局坐标系迭代之后，需要确定机器人躯体运动轨迹。首先确定躯体重心目标位姿，以直线前进为例，根据前述蚂蚁在障碍柱堆的位姿确定躯体目标位姿为：

(5)

式中,L为预期前进距离，H为设定离地高度。

然后通过六次多项式拟合，确定躯体运动轨迹。最后，类同浅度不平地形下单足运动规划方法，进行即将由支撑相切向摆动相的核心三足的运动规划，在该半个周期结束时探测、确定一个新的三角形进行下一次迭代。此后，可依次循环上述步骤。

4 样机试验

为了对本文所提算法进行研究，分别对仿生六足机器人样机在台阶和斜坡这两种非结构地形的运动进行试验验证，试验过程的截图分别如图5和图6所示。图5中的台阶高度为130 mm，而机器人离地高度为200 mm，此时H>h，可以认为该地形属于浅度不平地面，因而采用本文3.1节所提出的算法进行规划。从图5中可以看出六足机器人成功登上了台阶，并在此过程中保持机体处于水平状态。图6中的斜坡角度为15°，由于斜坡较长，其最高处已经超过了机器人离地高度，此时H

图5 六足机器人台阶运动试验

图6 六足机器人斜坡运动试验

图7 台阶试验中机器人左侧髋关节角度

图8 斜坡试验中机器人左侧髋关节角度

5 结论

本文通过对蚂蚁爬越障碍柱和障碍柱堆的两种运动过程的观察和分析，总结了蚂蚁在应对不规则地形时的运动策略，建立了更为合理的六足机器人的运动学数学模型。模仿蚂蚁在应对不规则地形时的运动策略，提出在进行运动规划时，将地形划分为浅度不平地形和深度不平地形两种情况，进而针对两种地形情况提出了六足机器人在不规则地形条件下的运动规划算法并分别给出了合理的数学算法。最后通过六足机器人样机在台阶和斜坡上的试验验证了本文所提算法的有效性。