地球静止轨道卫星碰撞碎片演化分析

(1.航天工程大学 研究生院，北京 101416； 2.航天工程大学 太空安全研究中心，北京 101416；3.中国人民解放军66350部队，河北 保定 071000)

0 引言

地球静止轨道(GEO)因其特殊轨道位置特点，已成为国际上众多大型卫星尤其是通信卫星的集中部署区，卫星和空间目标十分密集。截至2018年6月1日，美国空间监视网公布地球静止轨道航天器850个，还有许多空间目标以大椭圆轨道穿越该区域，另外大量无法观测到的空间碎片也分布在该区域[1]。这些空间目标密集地运行在海拔相差不到400公里，赤道两侧维度15°以内的球面约束的空间中，一旦发生碰撞将严重恶化日益严重的地球静止轨道环境[2]，对航天器构成严重威胁，甚至给地球静止轨道带来灾难性的影响[3]。

国外在航天器解体特性方面的研究比较成熟，通过对在轨撞击试验与地面撞击实验的统计分析，Reynolds等人于20世纪90年代末，拟合建立了“NASA标准解体模型”，该模型应用于NASA的EVOLVE4.0和LEGEND等空间碎片环境模型[4]。后来，改进后用在ESA的MASTER2009空间碎片环境模型[5]。2013年，德国Ernst-Mach-Institute的F.Schafer等开展了简单立方体卫星撞击解体的试验和仿真[6]。

国内许多学者也对空间环境、碰撞风险分析等方面有深入研究。中国空气动力研究与发展中心开展了多次超高速撞击解体试验，兰胜威和柳森等人对比了国外航天器解体模型的发展历程，并基于CSBM模型开发了航天器碰撞解体碎片分析软件SFA2.0[7-9]，哈尔滨工业大学的庞宝君团队对空间碎片环境预测算法等进行了研究[10-11]，国防科技大学的张斌斌和白显宗等人研究了碰撞预警与态势的相关问题[12-13]，航天工程大学李怡勇、王卫杰等人对空间目标的解体碎片的扩散特性进行了相关研究并评估了航天器撞击解体碎片的短期危害[14-17]。

本文基于NASA标准解体模型，对生成的碎片信息进行检验，选取符合要求的解体碎片数据，分析其演化规律。一旦GEO卫星发生碰撞解体，为分析新产生的碎片对GEO区域其他航天器的碰撞风险分析提供支撑。

1 碰撞相对速度分析

静止轨道空间碎片的轨道倾角在摄动作用下会在±15°[18-19]内发生周期变化，运行在GEO附近的卫星如果与轨道倾角为15°的空间碎片发生碰撞，碰撞相对速度约为：802.6 m/s。俄罗斯的“闪电”通信卫星，运行轨道400 km×40000 km，倾角63.4°，近地点幅角270°。对于来自该轨道的空间碎片，如果近地点幅角发生漂移，当近地点幅角超过330°时，该碎片会穿越GEO区域，当近地点幅角为345.037°时，该碎片轨道会与GEO交会，此时，与GEO区域的卫星碰撞概率最大，假设在交会点处存在一个GEO卫星，则碎片相对卫星的速度为2980.6 m/s。

碰撞相对速的计算如图1所示。碰撞相对速度确定的关键是根据开普勒轨道六根数得到交会位置的速度矢量，即将图中的4个空间目标开普勒根数转换成空间目标的位置和速度。

图1 碰撞相对速度示意图

第一，根据开普勒公式:

M0=E0-esinE0

将空间目标交会处的平近地点角转化成偏近地点角，然后根据:

计算真近地点角f；

第二，令：幅角u=ω+f，据:

计算地心距；

第三，根据球面三角形公式计算空间目标在J2000坐标系下的位置(x,y,z)：

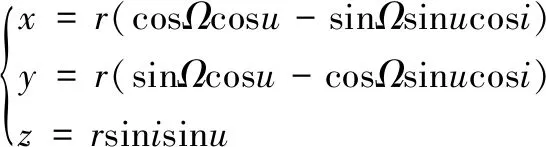
第四，据活力公式：

计算空间目标速度的大小，据空间目标角动量守恒：

h=r×v

计算位置矢量和速度矢量的夹角θ，故速度矢量与由地心指向升交点方向的夹角为：

uv=u+θ

第五，同第三步，据球面三角形公式，得速度矢量在J2000坐标系下三个坐标方向的分量：

对于第一步中的超越方程M0=E0-esinE0求解问题，有多种解法，常用的方法有简单迭代法和牛顿法。简单迭代法的迭代公式为：

Ek+1=M+esinEk,k∈N

牛顿法求解超越方程。定义函数：

f(E)=E-esinE-M

超越方程的根即为函数f(E)的零点。将f(E)泰勒展开，

因此，取迭代公式为：

无论是简单迭代法还是牛顿法，迭代初值可以简单选取，不妨取E0=M0，迭代终止条件为：|Ek+1-Ek|<ε，不妨取ε=1×10-12。经过验证，牛顿法比简单迭代法迭代次数要少，效率相对更高。故，选用牛顿法通过平近地点角求偏近地点角。

来自“闪电”轨道的空间碎片，当近地点幅角为345.037°时，该碎片轨道会与GEO交会，计算方法如下：

设空间碎片的近地点俯角取ω0时，其轨道与GEO存在交汇，则：当空间碎片的近地点角满足条件ω0+f0=π时，空间碎片的星下点维度为0，即：此时空间碎片处在其轨道与GEO的交点处。据此可计算得到ω0=345.037°。

2 解体碎片生成建模

空间目标高速碰撞会产生大量的空间碎片，根据空间目标碰撞前的运动状态和质量等参数，模拟生成的空间碎片的尺寸、面质比、速度增量等，建立碎片生成模型[20-21]。

2.1 NASA标准解体模型

撞击产生大于等于特征尺寸的碎片的数量为：

N(Lc) = 0.1mtot0.75Lc-1.71

式中，特征尺寸Lc为x、y、z三者的均值，其中，碎片最大长度记为x，与最大长度垂直的最大的长度记为y，与x-y平面垂直的最大长度记为z，解体部分的质量：

对于某一特征尺寸的碎片其面质比A/M的对数χ=lg(A/M)与特征尺寸的对数λc=lg(Lc)满足：

DA/M=α(λc)N(μ1(λc),σ1(λc),χ)+

(1-α(λc))N(μ2(λc),σ2(λc),χ)

其中:N为正太分布，其概率密度函数为：

对于航天器，相关系数为：

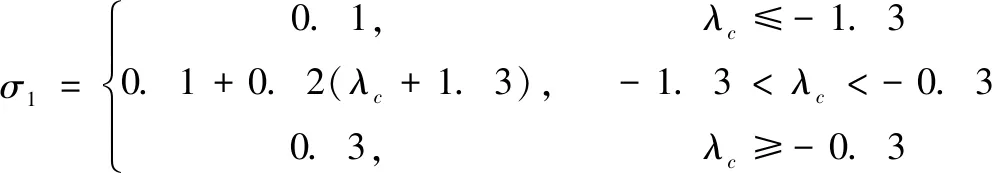
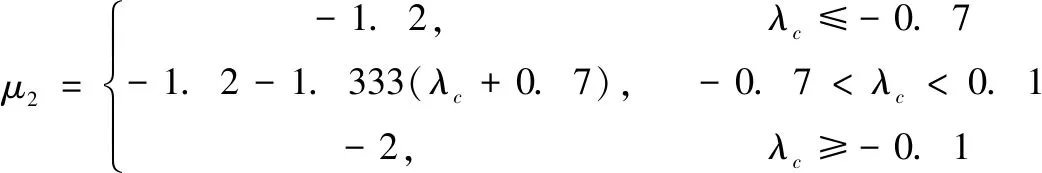
对于特征尺寸小于1.67 mm的碎片，假设其形状为正方体；对于特征尺寸大于1.67 mm的碎片，假设其为正方形。碎片平均截面积与特征尺寸之间的函数关系为：

撞击产生碎片的分离速度方向为全向均匀分布，分离速度增量的对数δ=lg(△v)满足：

D△v(χ,δ)=N(μ(χ),σ(χ),δ)

其中：

2.2 解体碎片仿真生成

碰撞解体事件遵循质量守恒定律，即解体后系统质量和等于解体前的质量和。碰撞解体事件遵循动量守恒定律，即解体后系统动量和等于解体前的动量和。

在对某一碰撞解体事件进行仿真时，仿真生成的数据具有随机性，为了增加仿真数据的可靠性，可对仿真生成的数据运用质量守恒定律进行检验，如果仿真生成的数据不满足质量守恒定律，则重新调用该模型，生成碎片数据，直到满足质量守恒定律。运用质量守恒定律对NASA标准解体模型检验的流程如图2所示。

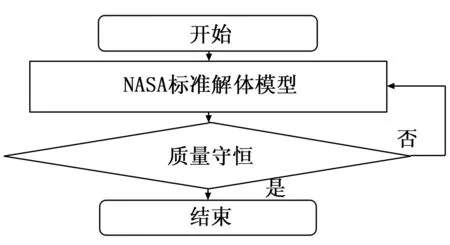
图2 运用质量守恒对NASA标准解体模型验证

将碰撞解体碎片的速度分解为原始速度和由于碰撞获得的速度增量两者之和。碰撞解体事件满足动量守恒一方面体现在碰撞解体碎片的原始速度v0的确定上，另一方面体现在碰撞解体后的系统的动量之和等于碰撞解体前系统的动量之和。该模型中，设定解体产生碎片的速度增量的方向满足全向均匀分布，对于完全解体事件，解体后的初始速度可通过动量守恒定律确定，即：

(mt+mp)v0=mtvt+mpvp

对于非完全解体事件，假定解体产生碎片的质量来源按照碰撞解体前两空间目标质量的加权获得，即解体部分来自两空间目标的质量分别为：

未解体部分的速度保持不变，解体产生的碎片的初始速度参照完全解体情形确定：

针对生成的仿真数据，无论是否完全解体，分别计算解体事件前后的动量和，如果不符合动量守恒定律，则舍弃重新运用该模型生成仿真数据，直到满足动量守恒。

3 解体碎片演变

空间目标碰撞产生的碎片会迅速向外扩张，形成碎片云，以碎片云的密度和形状作为参数描述演变过程，可将其分为球形、椭球形、绳形、螺旋线形、全方位扩散形和球壳形6个阶段。[22]

1)球形阶段。该阶段是解体初期碎片急剧向外扩张的过程。空间目标碰撞解体产生碎片获得的速度增量的方向服从各项均匀分布，在分离速度的作用下，空间碎片释放初期呈现球形。解体点为初始时刻空间碎片的球心，球心速度可通过动量守恒获得，碎片空间密度期望的峰值出现在一个球面上，该球面以解体速度增量的期望沿球径向扩散。该阶段，影响碎片云形状的主要因素为碎片的解体速度增量。

2)椭球形阶段。这一阶段碎片云在空间目标间的相对运动规律作用下碎片云的形状由球形变成椭球型。定义球形和椭球形阶段的分界点为0.05个轨道周期，椭球形阶段的起始时刻为：

3)绳形阶段。该阶段是指碎片云的形状沿椭球的半长轴拉伸，形成两头尖中间粗的绳形的过程。当分离速度的作用不能增大椭球在轨道法向和径向上的轴距，该轴距完全由相对运动规律决定时，椭球形阶段结束，绳形阶段开始。碎片在0.25个周期内沿各个方向的位移发生一次相位转换，比如初始沿轨道切向的位移最大的碎片，在经过0.25个周期后，位移变为0，此即为绳形阶段的起始时刻：

在此阶段，由于绳头和绳尾处碎片的轨道半长轴不同，他们之间的相对距离会越来越大。

4)螺旋线阶段。绳形阶段中，绳头与绳尾间的距离逐渐增大，当绳头追上绳尾，即绳头处的碎片轨道运行超过绳尾处碎片一圈，此时绳形阶段结束，开始螺旋线阶段。

设解体前空间目标的轨道半长轴a0，角速度n0，绳头处的碎片轨道半长轴a1，角速度n1，绳尾处的碎片轨道半长轴a2，角速度n2，解体碎片获得的最大速度增量△vmax，有：

a0-a1=a2-a0=°(a0)

则螺旋线阶段开始的时刻为：

故：

5)全方位扩散阶段。该阶段是指碎片向空间各个方向不断扩散的过程，摄动是主要作用力，一般认为碎片升交点赤经相差10°时进入全方位扩散阶段。当升交点赤经漂移率最大的碎片追上升交点赤经漂移率最小的碎片，全方位扩散阶段结束。全方位扩散结束时刻[10]：

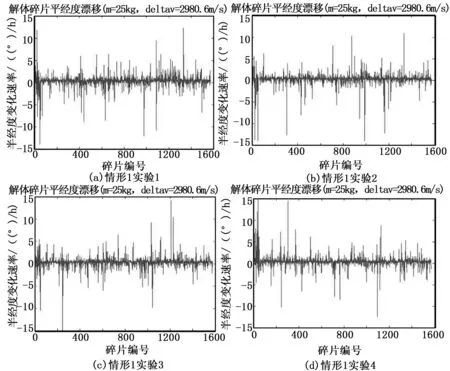
图3 情形一仿真实验

6)球壳形阶段。全方位扩散阶段结束，碎片在球壳内分布相对均匀，空间密度随时间变化不会发生较大变化，此即为球壳阶段。

4 算例仿真

解体碎片云的形状在演变过程中会经历六个阶段。全方位扩散阶段和球壳阶段的主要作用力是摄动，这两个阶段持续时间较长。螺旋线阶段的开始标志着平经度漂移率最大的碎片追上平经度漂移率最小的碎片，即：空间碎片蔓延到整个GEO区域，在地球赤道上空形成空间碎片的“环带”。螺旋线阶段的开始标志着空间碎片对整个GEO区域的航天器产生潜在的威胁。

引入发生碰撞两空间目标的质量比值k，k等于质量较小的空间目标与质量较大空间目标的质量之比：

显然，k∈(0,1]。

根据第1节确定的碰撞相对速度，运用NASA标准解体模型进行分析，若以802.6 m/s的相对速度发生碰撞，当k小于0.1242时，空间目标碰撞发生非完全解体；则对任意质量比值k大于等于0.1242时，空间目标碰撞发生完全解体。若以2980.6 m/s的相对速度发生碰撞，当k小于0.0090时，空间目标碰撞发生非完全解体；则对任意质量比值k大于等于0.0090时，空间目标碰撞发生完全解体。

选取SSN编号为36106的美国商业通信卫星与空间碎片发生碰撞进行分析。该卫星于2009年11月30日(UTCG)发射，运行在地球静止轨道，据2018年05月31日的TLE数据，2018年05月31日22:47.870星下点经度85°E，质量2550 kg。

4.1 完全解体仿真

4.1.1 情形一

假设该卫星与来自“闪电”轨道的碎片发生碰撞，碰撞相对速度2980.6 m/s，当k大于等于0.0090时，发生完全解体，计算知，当碎片的质量大于等于22.90 kg时，发生完全解体。当前情形下，不妨取碎片质量25 kg进行仿真，2018年6月1日0时，空间碎片轨道根数如表1所示。

表1 “闪电”轨道空间碎片轨道根数

仿真4次解体事件，计算解体产生的每一个碎片的平经度漂移率，横坐标表示碎片的编号，纵坐标表示碎片平经度漂移率，正值表示方向由西向东，负值表示方向由东向西，单位为：°/h，如图3所示。

从图中可以看出，该情形下的四次仿真，碎片的平经度漂移率普遍在5°/h以内，最大的接近15°/h，解体碎片云分别经过13.58 h、14.4 h、12.41 h和13.33 h后进入螺旋线阶段，即碎片会在赤道上空附近绕地球形成环带，标志着空间碎片对整个GEO区域的航天器产生潜在的威胁。

图4 情形二仿真实验

4.1.2 情形二

假设该卫星与运行在GEO附近的碎片发生碰撞，碰撞相对速度802.6 m/s，当k大于等于0.1242时，发生完全解体，计算知，当碎片的质量大于等于316.45 kg时，发生完全解体。当前情形下，取碎片质量320 kg进行仿真，2018年6月1日0时，空间碎片轨道根数如表2所示。

a/mei/(°)Ω/(°)ω/(°)M/(°)265560000.677863.4336.600

仿真4次解体事件，计算解体产生的每一个碎片的平经度漂移率，横坐标表示碎片的编号，纵坐标表示碎片平经度漂移率，正值表示方向由西向东，负值表示方向由东向西，单位为：°/h，如图4所示。

从图4可以看出，该情形下的四次仿真，碎片的平经度漂移率普遍在5°/h以内，最大的达到25°/h，解体碎片云分别经过8.57 h、14.12 h、14.4 h和15.65 h后进入螺旋线阶段，即碎片会在赤道上空附近绕地球形成环带，标志着空间碎片对整个GEO区域的航天器产生潜在的威胁。

4.2 非完全解体仿真

4.2.1 情形三

假设该卫星与来自“闪电”轨道的碎片发生碰撞，碰撞相对速度2 980.6 m/s，由2.6.1.1的分析知，当碎片的质量小于22.90 kg时，发生非完全解体。当前情形下，取碎片质量10 kg进行仿真，2018年6月1日0时，空间碎片轨道根数如表所示。

仿真4次解体事件，计算解体产生的每一个碎片的平经度漂移率，横坐标表示碎片的编号，纵坐标表示碎片平经度漂移率，正值表示方向由西向东，负值表示方向由东向西，单位为：°/h，如图5所示。

从图6可以看出，该情形下的4次仿真，碎片的平经度漂移率普遍在2°/h以内，较完全解体的两种情形漂移率小，解体碎片云分别经过60 h、12 h、25.71 h和32.73 h后进入螺旋线阶段，即碎片会在赤道上空附近绕地球形成环带，标志着空间碎片对整个GEO区域的航天器产生潜在的威胁，不过该情形产生的空间碎片的数量较完全解体的情形要少的多。

4.2.2 情形四

假设该卫星与运行在GEO附近的碎片发生碰撞，碰撞相对速度802.6 m/s，由2.6.1.2的分析知，当碎片的质量小于316.45 kg时，发生非完全解体。当前情形下，取碎片质量10 kg进行仿真，2018年6月1日0时，空间碎片轨道根数如表1所示。

仿真4次解体事件，计算解体产生的每一个碎片的平经度漂移率，横坐标表示碎片的编号，纵坐标表示碎片平经度漂移率，正值表示方向由西向东，负值表示方向由东向西，单位为：°/h，如图6所示。

从图6可以看出，碎片的平经度漂移率普遍在1.5°/h以内，4种情形中该情形下碎片的平经度漂移率最小。该情形下的4次仿真，解体碎片云分别经过51.43 h、83.72 h、72 h和102.86 h后进入螺旋线阶段，即碎片会在赤道上空附近绕地球形成环带，标志着空间碎片对整个GEO区域的航天器产生潜在的威胁，但该情形产生的空间碎片的数量较前三种情形要少的多，对GEO区域航天器的威胁要小的多。

图6 情形四的仿真实验

5 结论

通过第4节4种情形16次仿真实验的结果来看，有14次实验新产生的碎片在3天内扩散到整个GEO区域，另外两次实验，新产生的空间碎片也近乎扩散到整个GEO区域。对于来自“闪电”轨道的空间碎片与GEO卫星发生碰撞的情形，两者相对速度约2.98 km/s，相对速度较大，通过仿真实验可知，碰撞极易发生完全解体，产生大量空间碎片，新产生的空间碎片迅速漂移到整个GEO区域。

对于来自GEO区域的空间碎片与GEO卫星发生碰撞的情形，两者相对速度较小，最大碰撞相对速度约0.8 km/s，只有较大质量的空间目标与GEO卫星发生碰撞，才会导致卫星完全解体，比如情形二中，只有当空间碎片质量达到320 kg的时候，与编号36106的航天器发生碰撞才会产生大量空间碎片。通过仿真实验可知，较小质量的空间碎片与GEO卫星发生碰撞产生的空间碎片对GEO区域的短期影响相对较小，不过产生的少量空间碎片对GEO区域的长期影响有待进一步研究。