轨道图像特征点规律分布研究

(上海工程技术大学 城市轨道交通学院，上海 201620)

0 引言

轨道近景摄影测量技术能够实现对各轨道部件几何状态的检测及轨道空间线形的测量，是轨道无接触、动态实时检测的发展趋势。然而轨道近景摄影技术由于拍摄角度及拍摄距离的影响，单幅图像中包含的轨道区段长度有限，此时需要将多幅轨道图像进行匹配拼接，获得完整的轨道图像以提高检测效率[1-2]。由于有渣轨道图像具有图像色彩信息单一，图像背景复杂，特征分布多变的特点，使得轨道图像在匹配过程中容易造成误匹配，检测速度难以提高[3-5]。对轨道图像特征分布规律的研究，有利于对确定的轨道图像特征建立针对性的检测模型，提高图像匹配的快速性和准确性，对用图像实现轨道空间线形建模具有重要意义。

目前，国内外对轨道图像特征的研究主要集中在扣件区域，根据hough变换提取扣件直线特征进行图像匹配，但是少有涉及根据扣件细分及钢轨轨枕区域点特征的分布规律，利用更易获得的、数量较少的几个几何特征点进行图像匹配。

本文提出使用尺度不变的Harris特征点检测算法提取轨道图像的几何特征点，对得到的特征点用sift描述子计算其特征向量，在分析轨道图像部件特征及布设规律的基础上，运用分析统计的方法获得轨道图像间出现频率最高的同名点，实现轨道特征点分布规律的研究。

1 轨道区域划分

轨道结构主要由钢轨、轨枕、扣件等部件连接组成。如图1所示，钢轨、扣件及枕木分布密集、排列规律、均匀且几何特征明显，适宜作为轨道特征规律研究的有效部件；其他轨道部件由于布置间隔距离过长或分布不均匀，不适合作为轨道特征规律研究的有效部件[6-7]。

图1 轨道部件示意图

扣件相比于轨枕、钢轨结构更加复杂。主要由螺母、平垫圈、弹条、轨距挡板、挡板座等部分构成，且各个部分几何特征明显[8]。弹条Ⅱ型扣件结构如图2所示。

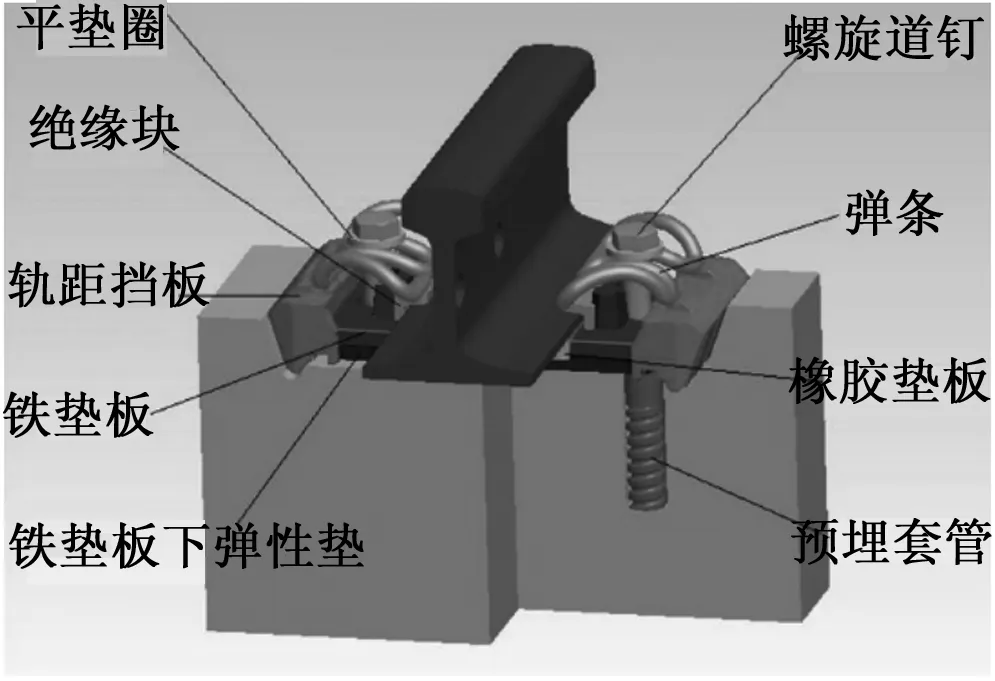
图2 弹条Ⅱ型扣件结构示意图

根据以上分析，螺母、弹条、挡板座、钢轨轨枕交叉处具有明显几何特征，可以推测出现几何特征点的频率较高。因此，将轨道图像划分为4个区域进行特征点分布规律研究：螺母区域、弹条区域，挡板座区域，钢轨轨枕交叉区域。

2 同名点匹配方法选择

Harris算子是Harris C和Stephens MJ提出的一种基于信号的特征提取算子[9]，该算子检测图像中每一个像素的兴趣值,通过分块选择可以使特征点分布均匀；并且检验到的特征点能够反映图形的结构。SIFT(scale invariant feature transform，SIFT)是GLowe D在2004年提出的基于不变量描述子的特征点匹配算法。SIFT检测算子具有良好的尺度、旋转、视角及光照不变性，特征描述子所含信息量丰富，并且匹配数量可控，精度高[10-11]。但是算法本身需要对图像进行多次分层卷积平滑操作，使得提取过程复杂且运算时间长，对像素量少的兴趣区域响应弱；并且获得的特征点无法反映图像的几何结构，即不是人眼可辩的特征点。

根据轨道图像部件的几何特征及布设规律，本文结合harris与sift算法，先对图像指定区域进行尺度不变的Harris特征点检测，再用sift描述子对特征点建立特征向量，根据合适的点确定同名点，完成匹配。

2.1 传统Harris特征点检测方法

2.1.1 Harris特征检测算子对特征点的定义分析

受morvaec算子的影响，harris算子认为特征点是区域像素在灰度值上的变化。所不同的是，harris不再局限于对邻域内水平、垂直、对角和反对角四个方向灰度变化的考察，而是考虑窗口沿任意方向移动时灰度的变化情况：在平坦区域，窗口沿任意方向移动，区域内图像灰度保持恒定；在边沿区域，窗口沿垂直边缘方向移动，区域内图像灰度差异性显著；在两条边缘相交的角点区域，窗口沿任意方向移动，区域内图像灰度差异性均表现明显。

Harris对特征点的定义符合本文要查找的人眼可见的轨道几何特征点特征。例如，轨道档板肩几何上是一个矩形长条，其有效的结构特征点为矩形的四个顶点，一阶微分后harris窗口在角点区域沿各个方向移动的响应均较大。

2.1.2 Harris检测算子原理分析

传统的Harris特征点检测算法受信号处理中自相关函数的启发，检测算子只涉及图像的一阶导数。建立M矩阵如下：

(1)

其中:Ix和Iy分别是图像I在x方向和y方向的梯度；G是高斯模板；⊗表示高斯模型和函数进行卷积运算。

为避免求解M的特征值，定义harris的特征点响应函数为：

R(x,y)=Det(M)-cTr(M)2

(2)

(3)

(4)

其中:det为矩阵行列式；tr为矩阵的迹(即矩阵对角线之和)；c为经验值，通常取0.04～0.06[12]。

2.1.3 尺度不变的harris检测算子

传统的harris检测算子对旋转平移等变换具有良好的稳定性，但是受图像尺度变化影响较大，较小的尺度变化会带来大量的错误检测。轨检车运行过程中由于钢轨踏面不平滑等原因产生震动，进而使检测相机抖动，由此摄影得到图像会有少许尺度变化。为克服检测过程中图像的尺度变化，找到不受尺度变化影响的几何特征点，本文引入尺度不变的harris检测算子。

借鉴mikolajczyk等人对传统harris特征检测算子的改进，现定义具有尺度适应性的harris二阶矩阵μ(x,y,δI,δD)为:

⊗

(5)

其中:(x,y)为像素点坐标，Ix和Iy分别为图像沿水平和竖直方向的一阶微分，δI为用于平滑图像的高斯核函数的积分尺度，δD为用于计算图像梯度的高斯核函数的微分尺度。并且δI=SδD，s为常数且s小于1。

将轨道图像按部件组成及分布情况分成不同小区域，对不同区域设定不同的阈值。以尺度空间为基础，分别在尺度域和空间域中搜索响应极值点。其具体步骤为：

1)预先定义一组积分尺度：

δ1…δn=δ0…knδ0

其中:k取1.4。通过确定积分和微分尺度，生成一组μ(x,y,δI,δD)。

2)进行位置空间搜索：

(1)对于给定的尺度空间，计算特征点响应函数，判断响应值是否大于阈值。

(2)对像素点进行8邻域最大值搜索，保留邻域内响应值最大的候选点。

3)进行尺度空间搜索：

(1)计算候选点的拉普拉斯函数响应，保留函数绝对值大于阈值的点为新的候选点。

(2)在相邻两个尺度空间中，将候选点与其邻域共26个点作比较，判断拉普拉斯响应是否为邻域内的最值点。

本文以弹条Ⅱ型轨道扣件为研究对象，典型的扣件图像如图2所示。由于轨道图像像素的单一性和背景的复杂性，使得轨道部件几何顶点及其交叉点成为稳定特征点可能出现的区域。分别用尺度不变的harris检测算子对扣件、螺母进行特征点检测，结果如图3所示。

图3 扣件、螺母特征点检测结果

2.2 特征点描述子

对用尺度不变的harris检测算子得到的特征点，用sift描述子计算其特征向量。

2.2.1 特征点方向分配

利用图像的局部特征给每一个关键点分配一个基准方向，采用特征点的3σ邻域窗口内像素的梯度和方向分布特征进行描述。梯度的模值和方向如下：

(6)

θ(x,y)=tan-1((L(x,y+1)-L(x,y-1))/

(L(x+1,y)-L(x-1,y)))

(7)

其中:L表示特征点的尺度空间，梯度的模值m(x,y)按1.5σ的高斯分布加成，按尺度采样的3σ原则，邻域窗口半径为3×1.5σ[13]。

建立方向直方图，统计特征点邻域范围各像素的梯度和方向，直方图的峰值表示该点邻域梯度的方向，定义此关键点的主方向为直方图最大值所对应的方向，并定义该点的辅方向为峰值大于主方向峰值80%的方向。

2.2.2 特征点特征描述

sift描述子是用一个128维向量表示，记录了关键点邻域8个方向的梯度信息。具体计算步骤如下：

1)对关键点所在尺度空间的邻域进行区域划分，将其分成d*d个子区域(本文设置d=4)，每个子区域有8个方向。

2)为保证图像的旋转不变性，旋转坐标轴到关键点的方向。关键点领域内各采样点旋转前与旋转后的坐标关系为：

(8)

(x,y∈[-radius,radius])

3)计算领域内各子区域全部像素的梯度值，将所有梯度值归并到8个方向上，并计算其权值。

4)确定每个特征点的特征向量。计算各子区域8个方向的梯度值，得到一个128维的梯度向量，此向量即为特征向量。

2.3 特征匹配

如前文所述采用尺度不变的harris角点检测提取轨道几何特征点，用sift描述子计算已知特征点的特征向量，则特征匹配的一般流程如图4所示。

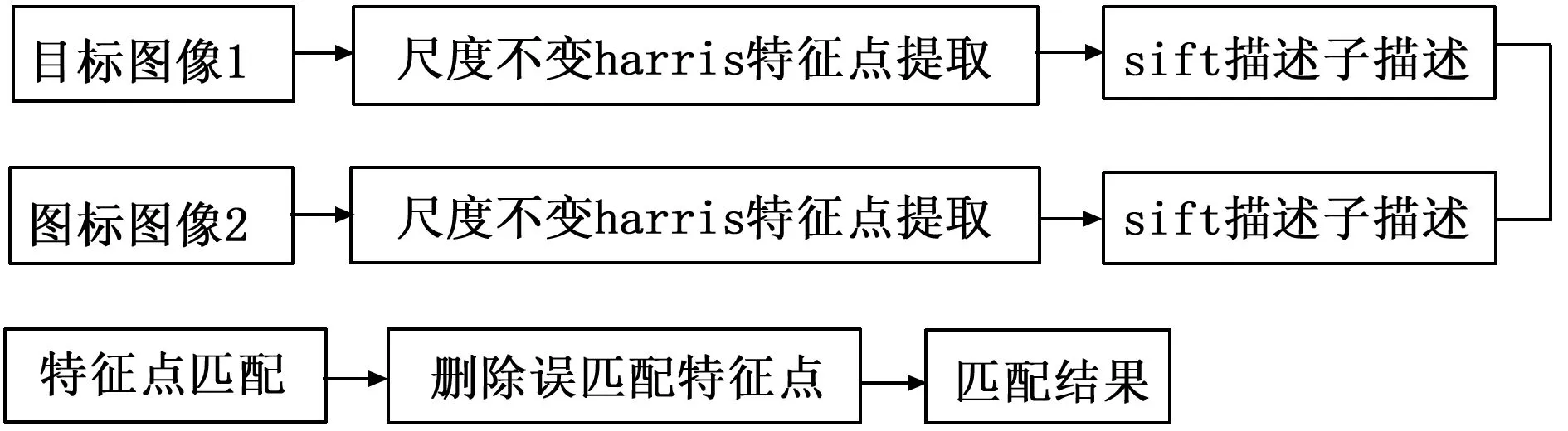
图4 特征匹配的一般步骤

本文采用欧氏距离作为特征向量的相似性度量准则。

(9)

其中:D值表示特征点之间的相对距离，值越小，表明两个特征点越相似。搜索策略：以待匹配图像A中的特征点为定点，采用邻近搜索法在待匹配图像B中搜索，找到距离最近和次近的两个特征点，计算他们之间的比值，若比值小于预先设定的阈值，则认为他们是同名点。运用随机抽样一致性算法对得到的同名点进行筛选，去除误匹配的点[14]。

3 统计分析得出特征点分布规律

在不同光照条件下对有渣轨道进行大量多角度摄影，根据轨道部件几何结构及其布设特点将轨道划分为不同兴趣区域。分别对每一区域进行harris-sift特征点匹配，统计具有物理几何意义的同名点出现频率，分析不同区域特征点分布频率高或者低的原因。

4 实验与证明

本文主要在matlab2016a版本上实现改进的harris-sift 轨道几何特征点的分布规律研究，实验数据均为实拍有渣轨道图像。

实验根据轨道布设及部件特点，将轨道图像划分为螺母区域，弹条区域，挡板座区域，钢轨轨枕交叉区域。分别对每一区域进行尺度不变harris特征点检测，用sift描述子计算特征点的特征向量并匹配，根据实验结果统计具有明显几何特征的同名点出现频率。

其中，为保证检测的几何特征点有效并且准确，在特征点检测过程中采用如下几条实验策略：

1)经验阈值k的选取影响候选特征点的个数及可靠性，不同区块选区的k值不同。

2)将harris候选点的兴趣值从大到小排列选取前50个点作为特征点(我们认为总能被检测到的特征点，其兴趣值应显著大于其他特征点)。

3)为避免不同区块内特征点聚簇现象，采用n*n窗口扫描图像，仅保留每次移动窗口内响应值最大的候选点为特征点。

对不同轨道图像区域检测及匹配结果如图5～8所示。

图5 挡板座块匹配结果图

图6 螺母块匹配结果图

图7 交叉块匹配结果图

图8 弹条块匹配结果图

对1000幅轨道实拍图像进行检测，特征点统计结果如表1所示。

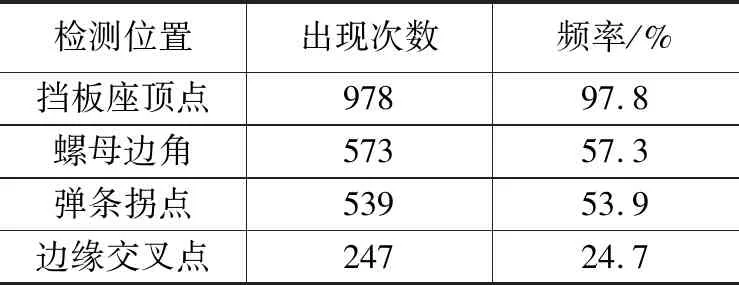
表1 特征点统计结果

由表1分析可知,选取前50个兴趣值最高的特征点作为考察点，挡板座顶点被检测到的次数最高，出现频率达到97.8%。螺母边角和弹条拐点被检测到的频率相近，由于两者灰度值相近且有阴影影响，使几何特征点的识别率较低。钢轨轨枕的边缘交叉点由于周围存在大量杂点使得特征点识别率低。

5 结论

1)通过对轨道图像统计分析,挡板座顶点被检测到的频率最高，达到97.8%。由于挡板座几何形态简单且规则(矩形长条)，适宜运用harris特征点检测方法选取特征点，并且其灰度值显著大于周围部件灰度值，微分结果显著。检测算子的旋转不变性让图像适应多角度摄影。

2)由于弹条以及螺母与轨距挡板灰度值相近，几何特征相对复杂，并且，由于部件间的相对位置，摄影光照必定产生图像阴影，使得此区域的几何特征点检测率低。

3)边缘交叉处图像背景复杂，轨枕处杂点像素较多，并且钢轨灰度值与轨距挡板相近，直接用harris检测特征点，前50个兴趣点难以观测到有用的几何特征点。

6 结束语

针对轨道图像色彩单一、背景复杂，单幅图像特征点多变且不准确的问题。本文提出结合尺度不变的harris特征点检测算子和sift检测算子的方法，将harris特征点反映物体几何特征的特点与sift描述子的旋转不变性、精度高的特点相结合。通过大量采样摄影和统计分析，确定轨道图像中出现频率最高的同名点，实现轨道图像特征点分布规律的研究，得出结论：挡板座顶点出现频率明显高于其他区域几何特征点。