测试性验证试验的故障注入方法优化研究

(1.中国人民解放军92941部队 41分队，辽宁 葫芦岛 125001；2.中国人民解放军92941部队 43分队，辽宁 葫芦岛 125001)

0 引言

随着舰炮制导弹药的发展，其测试性作为质量监测的重要特性，以及维修保障性能的主要设计特性之一，越来越引起使用方和承制方的重视。测试性验证试验是舰炮制导弹药测试性水平的主要验证手段，故障注入作为验证测试性水平的一种有效方法，受到国内外研究人员的高度重视，如何进行故障注入方法的优化和减少故障注入的成本成为亟待解决的问题。故障注入是指人为地产生故障，以加速系统出现错误或失效，其方法一般分为基于硬件的故障注入、基于软件的故障注入和基于仿真的故障注入。以上三种方法各有优劣，直接对硬件进行故障注入虽然获得结果相对真实，但会对装备造成损伤；软件故障注入成本较低，而且不会对装备造成损伤，但是可实现的故障有限；基于仿真的故障注入虽然可以解决故障注入量的问题，但准确性不高、可信度差。

工程研究人员开发了大量的故障注入系统，用于验证装备或系统的可靠性和容错性。韩国航空大学提出了基于System C运行高效的混合故障注入环境SyFI[1]。Jin-fu Chen[2]等提出了一种基于故障注入模型的测试策略，可有效检测组件漏洞，且故障检测率大于90%。Shao C[3]等提出了一种针对故障注入的加密电路安全测试方法，实验结果证明了该方法的有效性。Wang G H[4]等建立了一种基于故障注入的可测试演示平台，能提高测试性验证试验的效率。Arasteh B[5]等提出了一种基于使用遗传算法的软件故障注入方法，比随机注入的结果更稳定、更准确。Yang C[6]等提出了一种引传动控制系统安全检测与故障诊断的故障注入策略。Wu J[7]等提出了一种混合故障注入模型，评估了故障预测模型。Li H[8]等提出了一种等效故障选择方法，解决了测试性试验中部分故障模式不能注入的问题，对比等效故障和原故障发现此等效故障选择方法是可行的。Cui X[9]等运用ATPG方法得到了寻找最优等效故障模式的方法。陈然[10]等提出基于层次模型的可更换模块故障注入方法，有效解决了测试性验证试验中故障不可充分注入的问题。江建慧[11]分析了故障传递特性，并深入研究了故障传播机理。针对关联复杂系统的故障诊断问题，宋志平[12]等提出了用状态关联矩阵建立状态树，对故障传递特性进行补充。陈杰[13]等提出了一种基于故障传递矩阵的故障隔离方法，有效解决了复杂系统故障诊断的问题。李天梅[14]等分析了故障之间的传递特性，运用贝叶斯信度传播算法理论，提出了位置不可访问的故障注入方法，提高了故障覆盖率。

1 故障注入方法优化分析

由于某型舰炮制导弹药存在部分故障无法注入的问题，因此可通过研究故障传递特性，得到测试性等效故障，然后用等效故障代替无法注入的故障，提高故障覆盖率。

1.1 故障与状态间的关系

根据被试装备研制总要求规定的测试性指标，按照GJB2072-94[15]等相关标准规定的试验方法进行测试性考核，当自然故障样本量不足时，须采用模拟故障的方式，以满足样本量需要。假设从某型舰炮制导弹药的故障样本中抽取n个故障模式进行故障注入，组成故障集F。

F={f1,f2,...,fi,...,fn}

(1)

UUT的状态由m个信号参数组成，用向量V表示：

V={v1,v2,...,vi,...,vm}

(2)

得到故障与状态的相关矩阵RFV如下：

(3)

式(3)中，rij表示故障与状态参数之间的相关性，取值为1或0。当rij=1时，该故障的发生会引起状态参数突变；当rij=0时，则相反。

1.2 故障间的相关性分析

由于系统各部件之间联系紧密，一个部件的故障必然会引起其状态信号异常，可能导致下一个或几个相邻部件同时发生故障，因此，故障是具有传播特性的。通过故障所对应的故障状态信号分析，可以得到基于测试性的等效故障矩阵EFF：

2)掘进机机身静止时，横滚角和俯仰角均在0.4°以内，航向角的变化在0.2°以内；在动态试验中，航向角的变化曲线基本与旋转台匀速运动的方位角曲线斜率相同。

(4)

式(4)中，eij代表故障fi与故障fj之间的等效关系，取值为1或0。当eij=1时，表示两个故障引起的状态变化相同，那么故障fi是故障fj的一个等效故障；当eij=0时，则两个故障不是等效故障。

为了进一步描述故障与状态、故障与故障之间的准确关系，需要确定矩阵RFV和EFF中元素的值。RFV可通过模糊概率Petri网[16]以及相关算法得到。由于某型舰炮制导弹药结构复杂，故障之间的关系相对复杂，存在很多不确定因素，需要借助贝叶斯网络多树传播算法确定EFF。

2 贝叶斯网络多树传播算法

多树传播算法是指在贝叶斯网络中每处节点分配一个处理器[17]，综合相邻节点传递的故障信息以及处理器内部的条件概率信息进行计算，求出各节点的后验概率值，然后按照此规律继续传播。

假设在贝叶斯网络中，各变量取值为1或0，其中“1”表示发生故障或处于故障状态，“0”表示未发生故障或处于正常状态。节点B可表示为有限集B=(B1,B2)，且B1与B2互斥，其中B1=1，B2=0。Bi(i=1,2)的信度计算公式如下：

BEL(Bi)=τφ(Bi)θ(Bi)

(5)

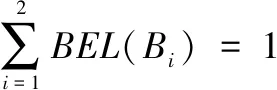
定义1：故障行为状态向量(BC)

在1.1节中的矩阵RFV中的第i行中所有取值为1的元素组成的向量组成故障fi对应的行为状态向量BCi。

在网络推理中，修改节点B的信度大小时需要考虑其父节点A的传递信息θB(A)以及各子节点的传递信息φ1(B)，φ2(B)，…

(6)

式(6)中，μ为归一化因子。在贝叶斯网络传递中，信度可传递给子节点和父节点，从子节点B自下而上传递给其父节点A的信息如式(7)：

(7)

从父节点A自上而下传递给子节点B的信息如式(8)：

(8)

先按照式(7)计算自下而上向父节点传递的信息为φ，然后根据式(8)计算自上而下向子节点传递的信息θ，按照此方法计算全部节点的信息，根据式(5)可计算得到各故障节点的信度值。如果计算得到的信度值高于其先验值，则求解此故障对应的行为状态向量BCi′，并与已经得出的行为状态向量BCi对比，如果满足BCi=BCi′，则两个故障互为等效故障，且在等效矩阵EFF中的对应元素为1；相反，则对应元素为0。根据以上的方法进行多次计算，可得到故障等效矩阵EFF。那么，等效故障也能清晰地在矩阵EFF上反映出来。

3 案例分析

3.1 某型舰炮制导弹药主要故障模式分析

根据大量试验数据显示，发现射击试验的主要故障是近弹(未达到目标所在位置提前掉地)，成为试验失败的主要原因[18]。制导弹药首次投入战争是在1991年的海湾战争，由于探测器件、惯性器件、电子器件、控制器件及动力装置等部分结构复杂，在快速发展和受到广泛关注的同时也暴露出一些问题。

故障树分析(fault tree analysis，FTA)是系统可靠性分析和故障诊断的一种有效方法。将某型舰炮制导弹药的故障现象进行故障树分析，得到导致这一现象的具体故障模式，作为改进弹药性能的重要参考，进一步提升其可靠性与作战效能。具体如图1所示。

3.2 电动舵机系统FMECA分析

故障模式、影响和危害性分析(failure mode, effects and criticality analysis，FMECA)一般根据工程实践与总结得到。分析各子系统或子单元的故障模式对装备或系统的影响，得到装备系统性的故障列表，发现设计中的重要单元和薄弱环节，用于改进装备的设计。

电动舵机系统作为某型舰炮制导弹药的主要功能部件，在控制炮弹飞行弹道和增加射程方面具有举足轻重的作用。经过理论分析和调研实践，得到其FMECA分析如表1所示。

3.3 基于硬件和软件的混合故障注入

根据3.1节中某型舰炮制导弹药的故障模式分析，从故障样本中抽取了主要的故障模式进行注入，具体情况如表2所示：

表2中“成功隔离次数”指故障被准确隔离到LRU的次数，根据表中数据显示，基于硬件和软件实现的故障注入总次数为154次，被成功检测且隔离的次数为119次。此外，存在3个故障模式无法注入，测试的覆盖率为77.3%，故障注入率为85.7%，难以满足测试性验证的要求。

3.4 运用贝叶斯网络多树传播算法求解等效故障

前面介绍了贝叶斯网络多树信度传播算法，这一节以某型舰炮制导弹药各子系统的故障模式为例进行分析和计算。

图1 某型舰炮制导弹药故障树分析

功能模块功能故障模式故障原因影响检测方法24V直流电源提供24V电压无电压输出或电压过高或过低线路或接地端电阻损坏舵机系统无法正常工作电压值测量控制驱动器接收弹载计算机的控制信号,驱动电动机转动电机不按照指令转动控制电缆断路或控制模式出错(选择位置控制模式)无法按照控制指令驱动电机检查电缆和控制模式设置直流无刷电机为舵机系统提供扭矩扭矩或转速异常控制参数选用不当或绕组损坏舵效降低,系统滞后控制参数调整或电流和电阻值测量舵片张开锁定机构打开和固定舵片舵片抖动或卡死装配异常或结构尺寸超差舵片无法张开或转动观察装配间隙减速器扭矩传递减速器打滑或转动不均匀安装配合不精密扭矩输出不正常观察和尺寸检测反馈电位器反馈舵片偏转角度电位器反馈信息不稳定电位器磨损、接触不良或短接反馈异常,影响准确判断电阻值测量和线性度测量

以表2中电动舵机的“齿轮间隙过大f1”、“轮齿断裂f2”和“轴承失效f3”三个的常见故障模式进行分析，这三个故障对应的主要状态信号为“转速信号g1”、“噪声信号g2”、“振动信号g3”和“温度信号g4”。根据试验数据和专家经验得出故障与信号的关系如图2所示。

表2 某型舰炮制导弹药故障模式混合注入

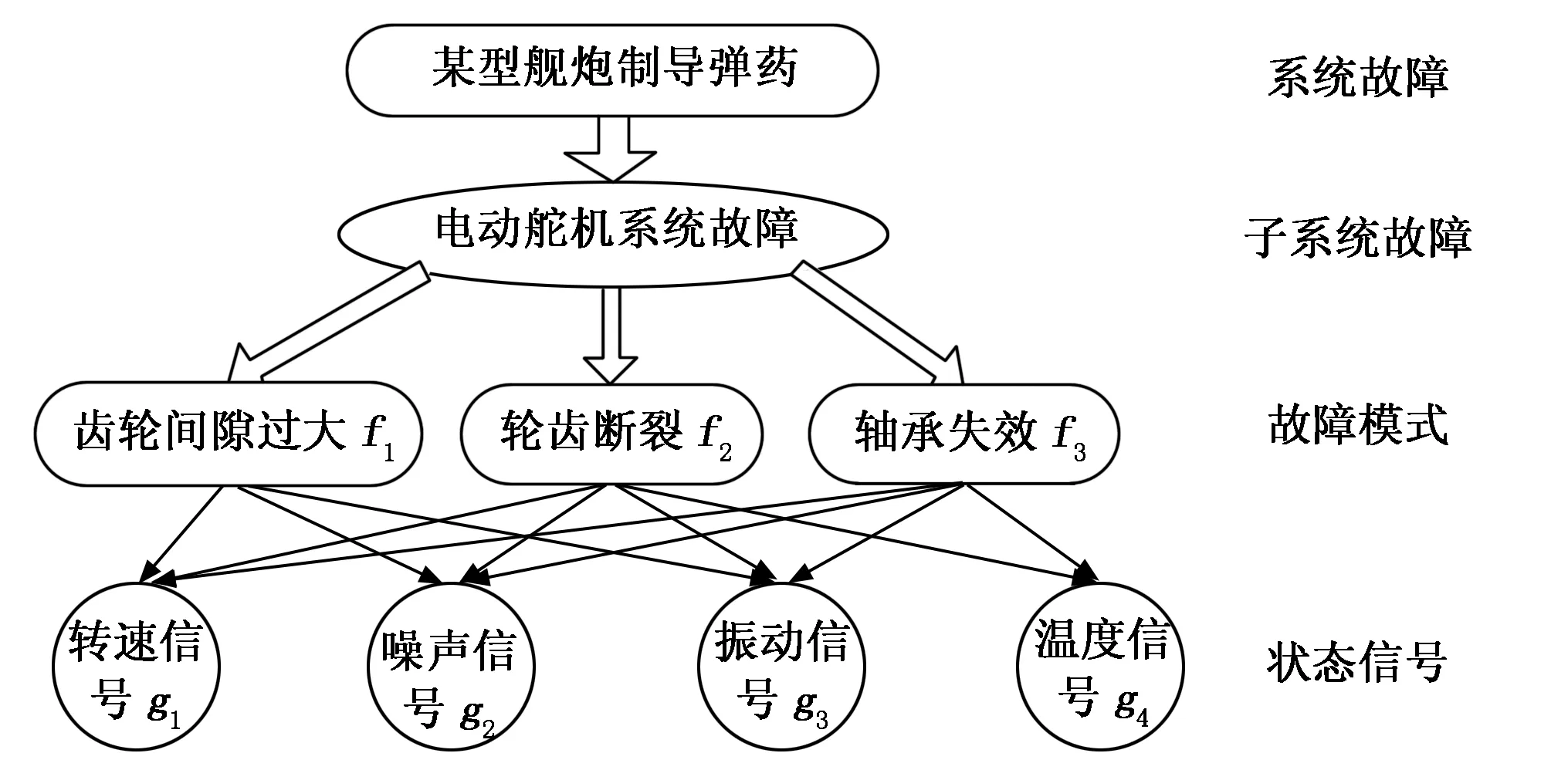
图2 故障模式与状态信号的关系

在试验信息的基础上得到贝叶斯推理的故障概率信息如下：

(9)

(10)

(11)

(12)

假设故障f1为已知的故障节点，且故障率为0.70，根据信度传递中贝叶斯条件概率计算得到各状态节点的信度大小如表3所示。

从表3中可以看出，在故障f1发生时，转速信号g1和噪声信号g2的故障信度超过了阈值。根据专家经验得到的贝叶斯反向推理网络的条件概率如下：

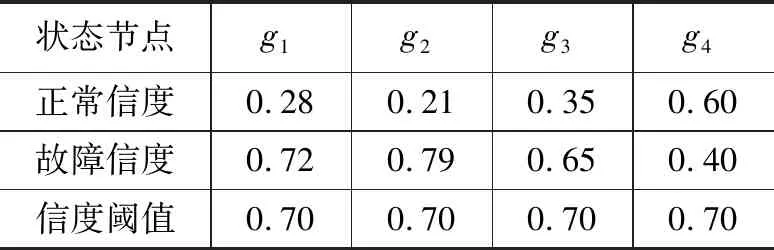
表3 各状态节点信度大小和信度阈值

(13)

(14)

(15)

(16)

假设在转速信号g1和噪声信号g2的出现异常的概率均为0.70，经过信度传递算法计算得到各故障节点的信度大小如表4所示。

表4 各故障节点信度大小和阈值

在转速信号g1和噪声信号g2的出现异常的情况下，f2故障信度大于阈值，而且在故障f2发生时，信号g1与g2也处于非正常状态。从而可以判断f2是f1的一个等效故障，从而可用故障f2代替故障f1，解决故障f1无法注入的问题。

同理，根据贝叶斯网络多树传播算法可得到故障模式f7和f19分别是故障模式f6和f21的等效故障，通过等效故障代替无法注入的故障模式，可将故障覆盖率从85.7%提高至100%，从而优化了故障注入方法。

4 结论

本文针对某型舰炮制导弹药封装严密，故障注入难度大，导致部分故障模式无法实现和故障覆盖率较低的问题，利用故障传递特性得到故障与状态、故障与故障之间的关系，并运用贝叶斯网络多树传播算法求解等效故障，最终实现了某型舰炮制导弹药主要故障模式的全部覆盖，使测试性验证试验更加完备，测试性水平的验证结果可信度更高。