四旋翼无人机控制系统仿真设计

杨则允1，李 猛，孙钦鹏

(1.山东龙翼航空科技有限公司，山东 济宁 272000；2.济南大学 自动化与电气工程学院，济南 250022)

0 引言

四旋翼无人机是一种性能优越的六自由度无人飞行器，具有结构简单，体积较小，且飞行平稳、隐蔽性好等优点，与固定翼无人机相比较，它可以完成垂直起降、定点悬停、低速飞行等一些特殊功能。随着无人机的各项关键技术的发展，四旋翼无人机已慢慢向多功能化和高效的方向发展，无论是在军用领域或是民用领域，四旋翼无人机都以其优越的性能和广泛的用途凸显出独特的价值，可应用于救援搜索、侦查监控、探查航拍等各领域，因此对四旋翼无人机的研究具有重要的学术价值和现实意义[1]。

对于四旋翼无人机的研究涉及到飞行力学、电气传动、机械结构、自动控制理论、传感器技术等多学科、多技术领域[2]。控制系统设计是四旋翼无人机研制过程中的关键环节，包括系统建模、控制算法设计、仿真验证、软件和硬件开发等步骤[3-4]。控制系统设计的目的是实现无人机的精确飞行控制，包括精确控制无人机姿态，令无人机按照预定速度和位置进行飞行等。四旋翼无人机是一个六自由度的复杂运动体，是典型的欠驱动系统，具有典型的强耦合和非线性特性。因此，对飞行控制系统进行深入研究和设计开发，是四旋翼无人机研究研制过程中的核心环节。国外发达国家对四旋翼无人机的相关研究起步较早，美国宾夕法尼亚大学GRASP实验室研制的一种可以在室内进行低速飞行的四旋翼无人机，可在室内实现翻转、稳定飞行、着陆、目标识别和壁障等功能，具有很强的鲁棒性和控制稳定性[5]。澳大利亚卧龙岗大学的McKerrowDragantlyer对四旋翼无人机进行了精确的数学建模[6]。我国众多研究人员也对四旋翼无人机进行了大量的研究工作，刘伟分析了四旋翼无人机飞行原理，并建立了线性化的动力学模型，最后设计了双回路控制器，通过Matlab仿真验证了控制器的稳定性和有效性[7]。周德新、臧皖晋分别研究了四旋翼无人机的控制系统仿真设计[8-9]。姚元鹏分析了无人机飞行原理，并建立了四旋翼无人机动力学模型，然后对该模型进行了线性化简化；最后采用双回路设计了控制器，通过Matlab仿真验证了控制器的稳定性和有效性[10]。

本文针对四旋翼无人机的飞行控制问题，首先通过对其进行动力学和运动学分析，建立数学模型，控制系统采用四通道、多闭环的控制结构，实现了无人机的姿态控制、速度控制与位置轨迹控制，进行了四旋翼无人机的控制器设计，分别设计了高度控制、俯仰控制、滚转控制与航向控制通道，最后在Simulink环境下对设计的控制系统进行仿真实验。

1 四旋翼无人机飞行原理及建模

1.1 飞行原理

四旋翼无人机的4个旋翼固联在十字交叉机身上，由分别安装于十字交叉结构的顶端上的4个电机驱动。如图1所示，机载电机分为前后(电机2、电机4)和左右(电机1、电机3)两组，两组旋翼旋转方向相反，其中一组为顺时针，另一组为逆时针旋转，因此能够抵消螺旋桨互相之间的反扭力矩。四旋翼无人机是具有4个输入、6个输出的高度非线性、多变量的欠驱动系统，其角运动与线运动之间具有约束关系，即无人机的横滚、偏航、俯仰姿态是受到无人机位置误差约束。同时，四旋翼无人机是一个具有强耦合特性的被控对象，一个旋翼的转速改变将引起最少3个方向上的运动。

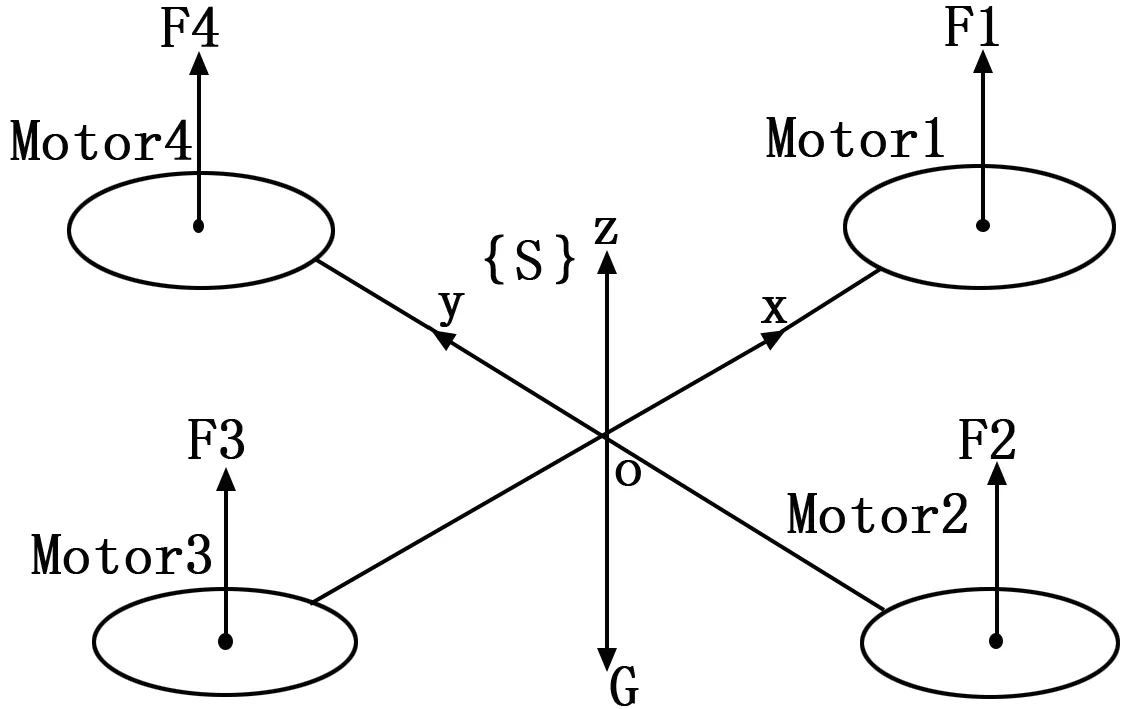
图1 四旋翼无人机飞行原理图

当按照不同的策略对旋翼电机转速进行调节时，机身的受力平衡会被打破，使得无人机姿态改变，进而产生相应的运动。四旋翼无人机在空间中具备的4种基本运动状态。

1)垂向运动：同时增加4个电机的输出功率，旋翼转速增加，总升力增大，四旋翼无人机便离地垂直上升；反之，同时减小4个电机的输出功率，四旋翼无人机则垂直下降，直至平稳落地，实现了无人机的垂直运动。当外界扰动量为零，且旋翼产生的升力等于无人机的自重时，无人机便保持悬停状态。

2)纵向运动和横向运动：实现无人机在水平面内纵向或者横向的运动，需要首先改变无人机的飞行姿态。增大无人机俯仰角，机体前倾，能够导致无人机的纵向运动。如图1所示，当电机3转速增大，其产生的升力也增大，同时减小电机1转速，使其升力减小，同时保持其它两个电机转速不变，反扭矩仍然保持平衡。无人机首先发生一定程度的倾斜，从而使旋翼升力产生水平分量，因此实现无人机的纵向前飞运动。由于四旋翼无人机结构对称，所以横向运动的工作原理与纵向运动完全一样。

3)偏航运动：四旋翼无人机的水平转动被称之为偏航运动，偏航运动可以借助旋翼产生的反扭矩来实现。旋翼转动过程中由于空气阻力作用会形成与转动方向相反的反扭矩。反扭矩的大小与旋翼转速有关。当4个旋翼转速相同时，4个旋翼产生的反扭矩相互平衡，四旋翼无人机不发生转动；当4个电机转速不完全相同时，不平衡的反扭矩会引起四旋翼无人机转动。

1.2 系统模型

机理建模法是对无人机各个部分的物理结构进行受力分析，经过理论计算得到线性或非线性的数学模型。本文采用机理建模方法，建立四旋翼无人机的运动学与动力学模型。

大地坐标系OgXgYgZg用来确定无人机的航向、姿态与相对起飞点的位置，其原点固定在大地上无人机起飞时的重心位置。机体坐标系OXYZ与机体固连，用来确定无人机在空中的姿态，其原点设在无人机重心处。可以通过绕X、Y、Z轴旋转到Xg、Yg、Zg轴的欧拉角θ、φ、ψ来确定机体坐标系和大地坐标系之间的转换关系。

1)动力学模型：

结合螺旋桨知识与空气动力学可将螺旋桨的推力F、空气阻力f、螺旋桨的转矩M和阻力矩τ分别表示为：

(1)

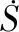
四旋翼无人机分别绕Xg轴、Yg轴、Zg轴转动的转动惯量为IX、IY、IZ。

(2)

(3)

无人机受到外界力和力矩的作用，形成线运动和角运动。线运动由合外力引起，符合牛顿第二定律，如公式(4)所示：

(4)

其中：r为无人机的位置矢量；Fx、Fy、Fz分别为沿OgXg轴、OgYg轴、OgZg轴3个方向上所受的升力；m为四旋翼无人机的重量。

2)运动学模型：

旋翼运动学模型描述的旋转包含横滚、俯仰和偏航3种角运动，这是刚体旋转产生的陀螺效应的三方面，陀螺效应由螺旋桨旋转再加上机体旋转引起，最后执行动作。

(5)

其中：无人机分别绕Xg轴、Yg轴、Zg轴转动的转动惯量为Ix，Iy，Iy，Jr表示螺旋桨的总转动惯量；Ωr=Ω1-Ω2+Ω3-Ω4表示对四旋翼中心矩；U1表示在Z轴方向总推力；U2表示横滚输入；U3表示俯仰输入；U4表示偏航输入。而且，Ui的值由下式确定：

(6)

由式(5)和式(6)可得四旋翼无人机的3个姿态角的运动学模型：

(7)

由牛顿第二定律可知，在大地坐标系下沿OgXg、OgYg、OgZg这3个方向上的直线运动方程为：

(8)

由式(6)知U1=F1+F2+F3+F4，且：

(9)

忽略空气阻力，并且把上述模型简化后得到非线性模型为：

(10)

2 控制系统设计

四旋翼无人机控制系统要达到的目的是使无人机在大地坐标系下的起点开始飞行，由设定的起始点按照期望的轨迹，平稳地飞行到目标点。为了达到控制目的，设计了一种四通道、多闭环的控制器结构，对四旋翼无人机进行轨迹控制和姿态控制。控制系统将四旋翼无人机的控制系统分为外环控制和内环控制两个部分，外环是轨迹控制回路，内环是姿态控制回路。

四旋翼无人机采用4个电机作为动力源，通过调节4个电机的转速。能够使无人机受力产生变化，进而改变无人机的姿态和位置。四旋翼无人机控制系统结构如图2所示。控制系统采用双闭环回路，分为外环控制和内环控制两个部分，外环是轨迹控制回路，内环是姿态控制回路。

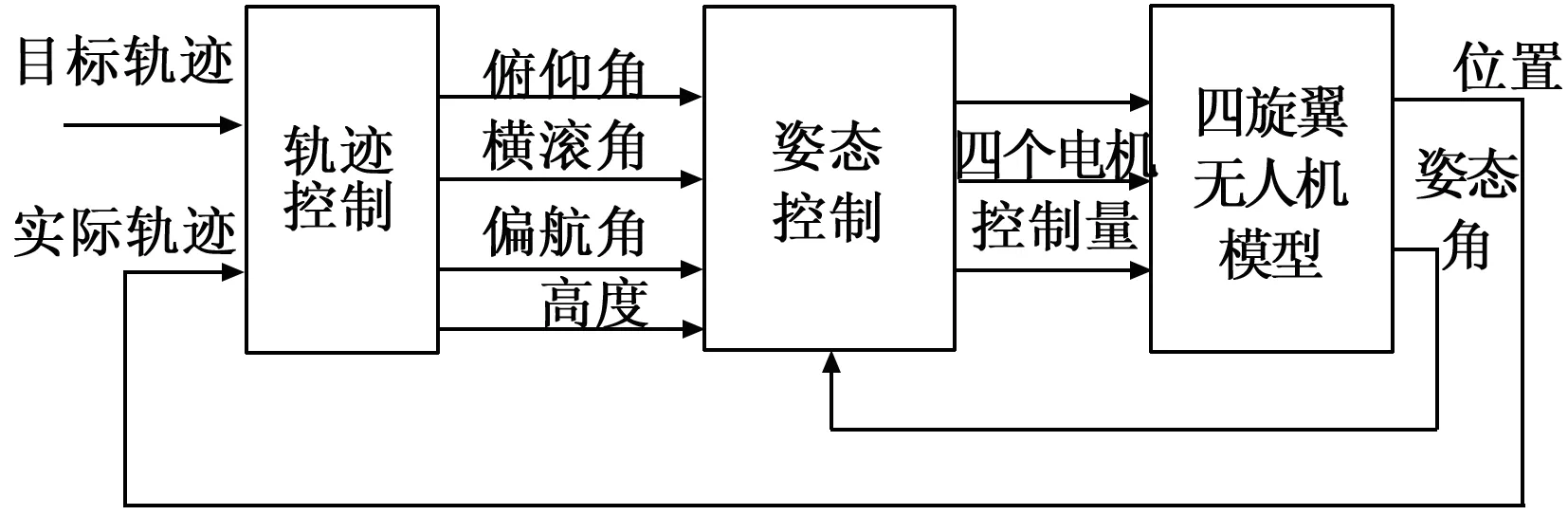
图2 四旋翼无人机控制系统结构图

2.1 姿态控制回路

四旋翼无人机的姿态控制是整个无人机控制系统中至关重要的内容。姿态控制回路设计的目的是让无人机的飞行姿态可以跟踪由轨迹控制回路计算得到的期望姿态，即四旋翼无人机在各种飞行条件下能够实现飞行姿态与期望姿态保持一致。

由图2可知，姿态回路是轨迹回路的内回路，轨迹控制回路的输出是姿态回路的输入，即期望的姿态角，并以无人机的实际姿态角作为反馈量，内回路输出对应无人机的4个输入变量即4个电机的转速。采用四通道的PID控制实现无人机的姿态控制回路设计。

姿态控制回路的输入为期望姿态角φd、θd和ψd，输出为U2、U3和U4，控制律设计如下：

(11)

其中：Kp1,Kp2,Kp3分别表示横滚、俯仰、偏航通道的比例系数，Kd1,Kd2,Kd3分别表示横滚、俯仰、偏航控制通道的微分系数。

2.2 轨迹控制回路

设计轨迹控制回路的目的是让无人机能快速、稳定以及准确的跟踪给定的位置轨迹。由图2可知，轨迹控制回路以期望的飞行轨迹为输入，以四旋翼无人机的实际位置为反馈，以四旋翼无人机的3个姿态角为输出。轨迹控制回路要计算出姿态控制回路所需的姿态角信号，然后由姿态控制回路完成对姿态角的跟踪控制。

首先利用期望位置与实际位置之差的比例控制解算出无人机沿X方向和Y方向的线速度，再利用期望的线速度与实际的线速度之差的比例积分控制解算出期望的姿态角。轨迹控制回路的输入为Xd和Yd，输出为和，控制律设计如下：

(12)

(13)

其中：Kpx、Kpy分别表示沿X、Y轴的位置控制回路中控制律的比例系数；Kpvx、Kpvy分别表示Vx、Vy速度控制回路中控制律的比例系数。Kivx、Kivy分别表示Vx、Vy速度控制回路中控制律的积分系数。

3 控制系统仿真实现

在MATLAB/Simulink平台上搭建四旋翼无人机系统仿真模型，如图3所示，包括轨迹控制、姿态控制、四旋翼无人机模型三部分。

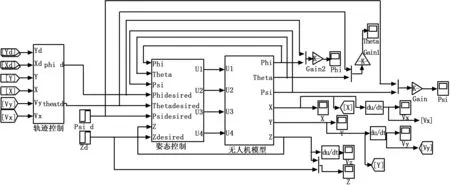
图3 四旋翼无人机控制系统仿真模型

3.1 姿态控制仿真

首先进行姿态控制仿真实验。设置姿态角的期望值为φd=5°,θd=0°,ψd=0°，对姿态控制回路参数进行整定，仿真结果如图4所示。其中虚线表示无人机姿态角的期望值，实线表示无人机姿态角的实际值。由图4可得，无人机系统能够快速响应并且较好地跟踪给定姿态角φd，且响应无超调，满足性能要求。同时无人机的俯仰角和偏航角保持稳定，一直输出为0，说明所设计的控制器较好的抑制了耦合问题，滚转角输入没有对俯仰角和偏航角造成影响。仿真结果表明，对于四旋翼无人机系统的模型，利用经典PID控制方法来设计控制器可以实现无人机的姿态控制。

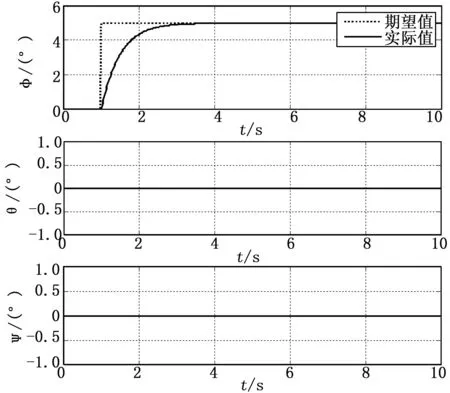
图4 姿态控制仿真图

3.2 轨迹控制仿真

在轨迹控制仿真中，设置期望的轨迹为高度4米的矩形路线。仿真结果如图5所示。

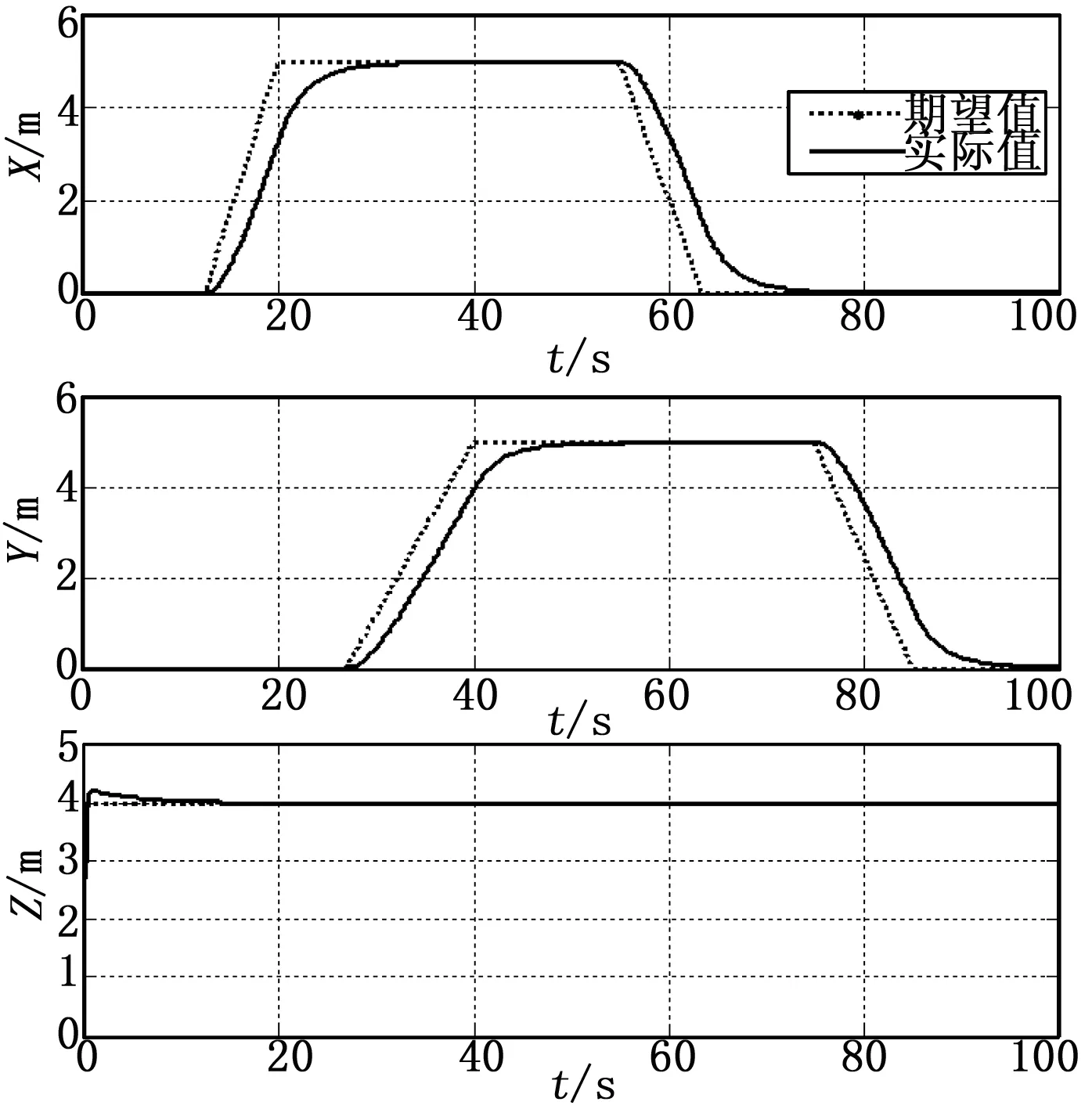
图5 位置控制仿真图

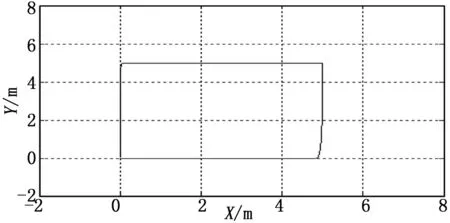
图6 实际飞行轨迹

图6中实线表示无人机的实际位置。由图5和图6可知，无人机在X方向和Y方向均能良好地跟踪给定的期望航线，在给定航线方向变化较快时，实际飞行位置与期望位置存在一定的滞后偏差。无人机的飞行高度(Z向)响应存在较小的超调，但很快的稳定在给定值。总体而言，四旋翼无人机系统能够快速响应并且较好的跟踪给定位置。

4 结束语

针对四旋翼无人机控制问题，论述分析了四旋翼无人机的飞行原理，建立了四旋翼无人机的运动学和动力学模型。控制系统采用四通道、多闭环的控制结构，实现了无人机的姿态控制、速度控制与位置轨迹控制，进行了四旋翼无人机的控制器设计，内环为姿态控制器，外环为轨迹控制器。分别设计了高度控制、俯仰控制、滚转控制与航向控制通道，在Simulink环境下对设计的控制系统进行仿真实验，仿真结果证明了对于四旋翼无人机的轨迹和姿态控制，本文所设计的方法是可行而有效的。四旋翼无人机的飞行控制技术还涉及到很多方面，除了本文研究的姿态控制和轨迹控制问题，还有对四旋翼无人机自主飞行和避障等方面的研究。关于四旋翼无人机的研究涉及到很多学科领域的技术和理论，今后还仍然有很多工作要完成，我们要为四旋翼无人机完成复杂的任务开展进一步研究。