基于自动搜峰和shannon熵的车辆轴承多普勒畸变故障声信号校正研究

(上海工程技术大学 城市轨道交通学院，上海 201620)

0 引言

滚动轴承是车辆(轨道车辆、汽车、电动车)必不可少的零部件，它承受着车辆牵引动力、制动阻力、齿轮啮合不良引发的附加载荷。这些载荷使车辆出现轴承故障频率较高，严重影响了车辆的运行安全。所以对轴承故障诊断意义重大[1]。

在道旁安置传声器阵列来获取运动轴承发出声音的故障诊断系统研究开始于1980年。在基于道旁声学检测的轴承故障诊断过程中，须使传声器安置位置与车辆之间有一段不可忽略的间隔，导致声源在传播过程中波长发生改变，传声器接收到的信号频率与声源发出的信号频率不同，从而会造成信号存在多普勒畸变。这种多普勒畸变会使测量信号在频域中产生频带展拓、频率转移等问题，使信号在频域中较难分析出声源所产生的故障特征频率，降低了故障诊断的可靠性和准确性[2]。为了解决多普勒畸变所带来的问题，国内外的许多学者对其进行了深入的研究。国外的Stojanovic 等利用锁相环技术矫正方法，使畸变信号在一定程度上得到了矫正，但该方法仍有一定的缺陷[3]。随后Johnson等改进了此方法，提出了PLL与DFE 算法相结合的校正方法[4]。国内的杨殿阁等研究出一种非线性时段映射的方式，实现了在时域中矫正信号[5]。张翱等利用能量重心法的特性，实现了多普勒畸变的矫正，在一定程度上提高了诊断精度[6]。

多普勒校正的关键在于对原信号进行重采样，获得重采样时间序列，通过瞬时频率估计方法可解决此关键[7]。目前使用最多的瞬时频率估计方法大致有3种，分别是：STFT谱峰搜索法、隐马尔科夫模型方法、分段最小二乘拟合方法。但这几种常用的算法都有其各自的缺点，如进行STFT谱峰搜索的瞬时频率时，采用了遮隔技术，大大增加了计算量，除此以外，还需提高频率分辨率。隐马尔科夫模型瞬时频率估计方法须采用大量的矩阵运算，运算量也较为复杂[8]。分段最小二乘拟合算法是根据在分段点位置判断是否为速度瞬变点来设定边界条件[9]。因此这几种常用的算法都有其各自的局限性。

由于STFT谱峰搜索法常应用在实际中，针对STFT谱峰搜索法所存在的计算量大且频率估计精度低等问题，本文提出一种基于自动搜峰和shannon熵的滚动轴承多普勒畸变故障声信号校正方法。首先对所采集的声音信号进行STFT时频分析；然后利用自动搜峰方法进行瞬时频率估计，设置shannon熵来提高瞬时频率估计精度，并得到拟合的瞬时频率曲线，进而得到信号重采样时间点；最后对原信号进行时域重采样，从而使畸变信号得以矫正。

1 多普勒效应

在传声器采集过程中，由于车辆基本匀速行驶，因此轴承声源的速度v可以近似看作是恒定的，如图1所示。由于轴承声源与传声器之间有一段的距离，从而造成传声器采集到的频率发生了改变，使信号在频域中发生频带展拓及频移，即道旁多普勒信号畸变。

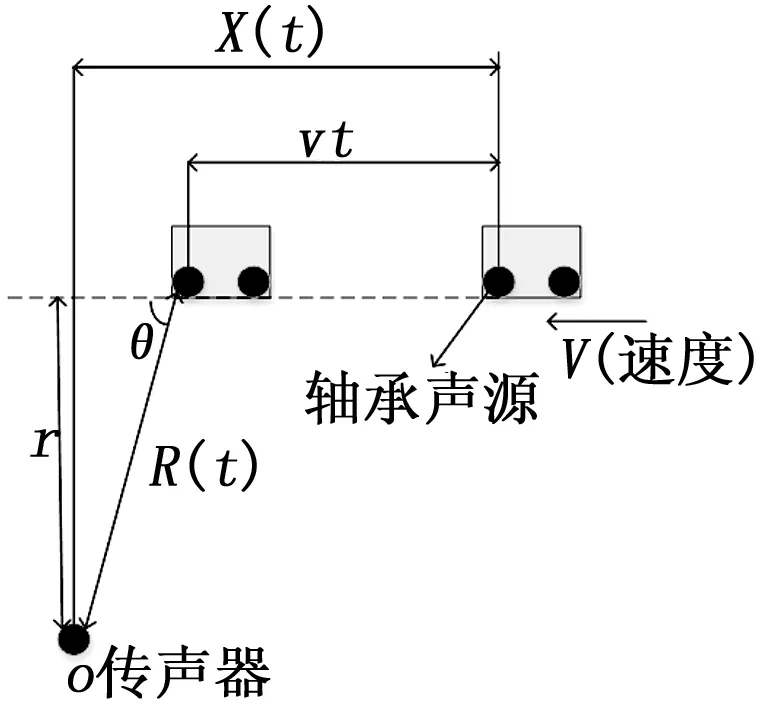
图1 运动模型示意图

在车辆行驶时，虽然车辆有多个轴承，但本文把整个车辆滚动轴承声源看作单声源。根据莫尔斯声学理论，传声器处采集到的声压P为传播距离衰减的声场辐射项C与近场效应D之和[10]，即：

P=C+D

(1)

其中：

(2)

(3)

其中:q单位时间内流过的物质的质量，q'=∂q/∂t，t为声源运动时刻，θ为声源运动方向与声源和传声器连线之间的夹角，R(t)为t时刻轴承声源与传声器之间的距离，c为声速，v为声源的移动速度，M=v/c为马赫数。

由于D值较小，可以忽略不计。因此采集到的声压为：

(4)

等号左右两边对相位进行求导，整理后可得出频偏率w。

(5)

式中，x为t=0时刻时声源位置与传声器位置水平距离，r为传声器到声源的垂直距离，f0为声源信号频率，f为传声器采集到的信号频率。由式(5)可以看出频偏率随时间非线性变换，传声器所采集的信号存在多普勒畸变。

2 校正理论与瞬时频率估计方法

2.1 基于瞬时频率的多普勒畸变校正原理

目前对多普勒畸变校正较多采用瞬时频率估计方法。在多普勒畸变信号中，假设原信号只存在f0频率，原信号的瞬时频率与采样频率存在如下关系[11]:

(6)

式中，fs为原信号采样频率，fsi为畸变信号i点处的采样频率，fi为畸变信号i点处的瞬时频率[12]。

根据采样间隔和采样频率的关系，即fs=1/dt，代入上式可得:

fi*dti=f0*dt=consti=1,…,N-1

(7)

式中，dti即为重采样时间间隔，重采样时间点为重采样时间间隔之和，即:

(8)

由于当重采样时间点达到畸变信号的时间点即可，所以定义最大重采样时间点tM,该值应满足的条件为：

(9)

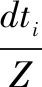
(10)

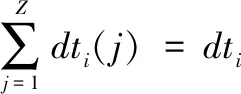
对任意区间内的Z个时段求和得：

(11)

可以发现，当Z越大时，上式可以变为：

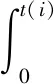
(12)

对上式进行求解，然后再通过三次样条插值便可得到矫正信号。

y=[y(ti(1))y(ti(2)) …y(ti(M))]

(13)

2.2 自动搜峰和shannon熵的瞬时频率估计

经研究，自动搜峰方法可以解决STFT谱峰搜索法存在的计算量问题，shannon熵可以提高瞬时频率估计精度。本文通过自动搜峰与shannon熵相结合进行瞬时频率估计。首先利用STFT局部平稳特性，从最低频率到最高频率进行局部自动搜峰，然后设置shannon熵提高瞬时频率估计精度。自动搜峰和shannon熵的瞬时频率估计流程如图2所示。

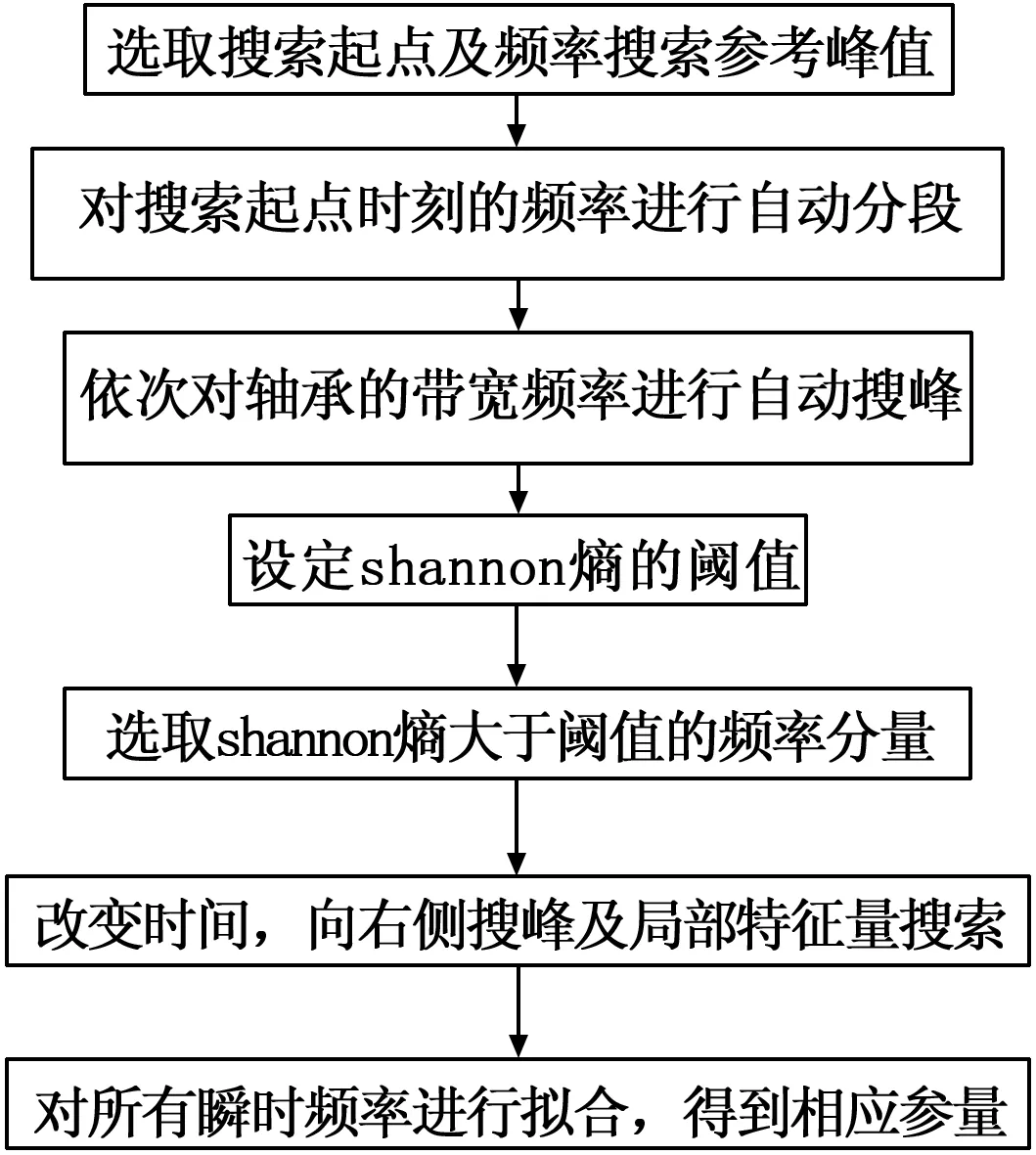
图2 自动搜峰和shannon熵的瞬时频率估计

具体步骤如下：

1)在STFT时频图上，把总时间平均分成N份，把频率长度平均分成 M份，以采集时刻tNB=0为起点，令fm=kfi，fm为频率搜索参考峰值，k为加权因数，也设置为N份。同时k可以控制频率点数；

2)对tNB时刻这一列的频率进行自动分段，即从最低频率到最高频率依次开始，当出现连续f(tNB,mi)≥fm时，搜索出Q个频段[13]，即，

Pj(tNB,hkj)=f(tNB,mi)

(14)

式中:Pj(tNB,hkj)为第j个声源分量所包含的频率数组；hkj=1,L,kj；kj为声源分量瞬时频率宽度，j=1,…,QQ为频带个数;

i=1,…,l1,l1+1,…l1+k1-1,…,l2,l2+1,…,

l2+k2-1,,…,lQ,lQ+1,…,lQ+kQ-1

(15)

3)依次对每一个声源频率数组Pj(nNB,hkj),j=1,…,Q，分别进行峰值搜索，得到相应的最大频率值。由于shannon熵可以衡量信息的价值，熵越大，不确定性越大，信息量越大[14]。因此可设置shannon熵来提高瞬时频率的估计精度，具体算法为:

(16)

其中：argmax表示取最大值；Pj(tNB,mMj)为最大频率峰值；H为shannon熵校准。

4)从tNB时刻，改变时间tg，向右侧重复步骤2)逐列进行自动搜峰，得到所有时间列的声源频率带宽。Pj(tNB,hkj)为第g个时间列中，第j个声源分量所包含的频率数组；hkj=1,…,kj;kj为声源分量瞬时频率宽度，g=1,NB-1,NB+1,…,N;j=1,…,Q。

5)对每一个声源带宽频率，分步进行峰值搜索，具体算法为：

(17)

其中：arg max 表示取最大值；Pj(tNB,mMj)为最大频率峰值；H为shannon熵校准。

2.3 基于自动搜峰和shannon熵的多普勒畸变信号校正方法

基于自动搜峰和shannon熵的多普勒畸变信号校正方法如图3所示。

图3 多普勒畸变信号校正流程图

具体步骤如下：

1)STFT时频及频偏率分析。通过STFT时频谱，确定出步骤2)所需求的频率搜索参考峰值fm。通过频偏率分析，确定加权因数k的范围。

2)运用基于自动搜峰和shannon熵瞬时频率估计。由2.2节所述方法，获得所估计的所有声源的瞬时频率；

3)最小二乘法非线性拟合。对所得的离散瞬时频率进行非线性插值拟合，得到瞬时频率拟合值；

4)时域重采样。通过拟合后的瞬时频率计算出重采样的时间点，从而消除多普勒畸变；

5)判断还原的信号是否校正。通过频域分析确定信号是否校正，若信号未能校正，则调整频率搜索参考峰值，重新进行瞬时频率估计。

6)频域分析。在频域中分析校正的信号来验证本文方法的可行性。

3 仿真验证

3.1 仿真试验

本文运用matlab软件创建仿真试验。为更好突出多普勒畸变效果，仿真3个声源信号，频率为f1=100 Hz，f2=200 Hz，f3=300 Hz。设定采样频率为10.24 kHz，设置仿真参数x=10 m,r=1 m,c=340 m/s,以及v=10 m/s，信噪比为5 dB。由于多普勒信号畸变在频域中突出，因此本文重点在频域分析。仿真的原信号如图4和图5所示。

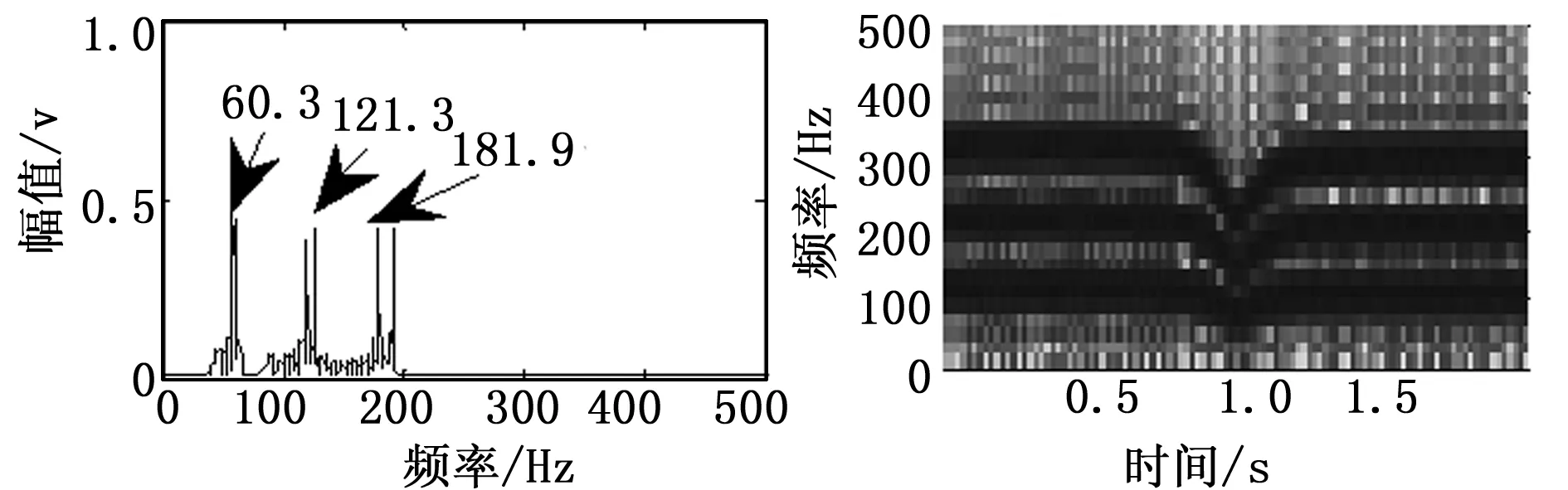
图4 仿真的原信号频谱图 图5 仿真的原信号STFT图

3.2 结果分析

由图4可以看出仿真的多普勒畸变原始信号频率发生了频移，100 Hz的频率移动至60.3 Hz，200 Hz的频率移动至121.3 Hz，300 Hz的频率移动至181.9 Hz，同时200 Hz的频率和300 Hz的频率也发生了频带展拓。由图5和图6可以看出瞬时频率随时间连续变化。在时刻t=0时，100 Hz频率出现在103 Hz处，因此搜索算法中设定103 Hz 为起始点，设定加权因数k为1.03-0.97(由频偏率图可知)，再通过自动搜峰和shannon熵的瞬时频率估计得到各段对应的瞬时频率。把序列自动分为512段(由计算速度和收敛性确定)，如图7为序列的shannon熵值。

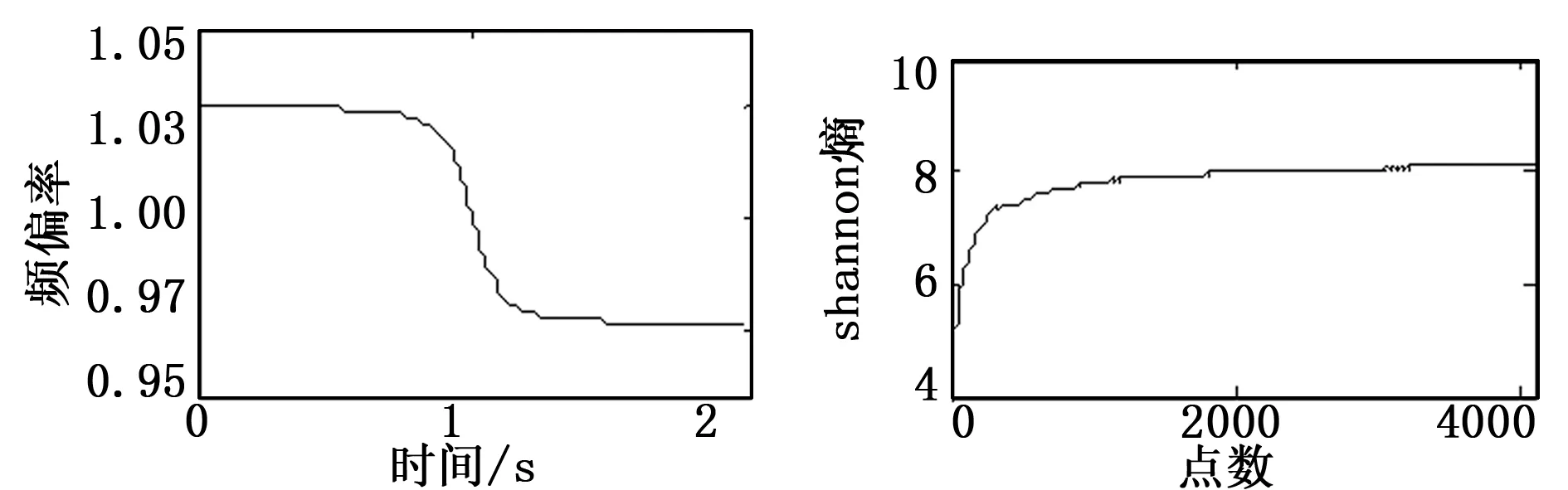
图6 仿真的原信号频偏率 图7 shannon熵校准

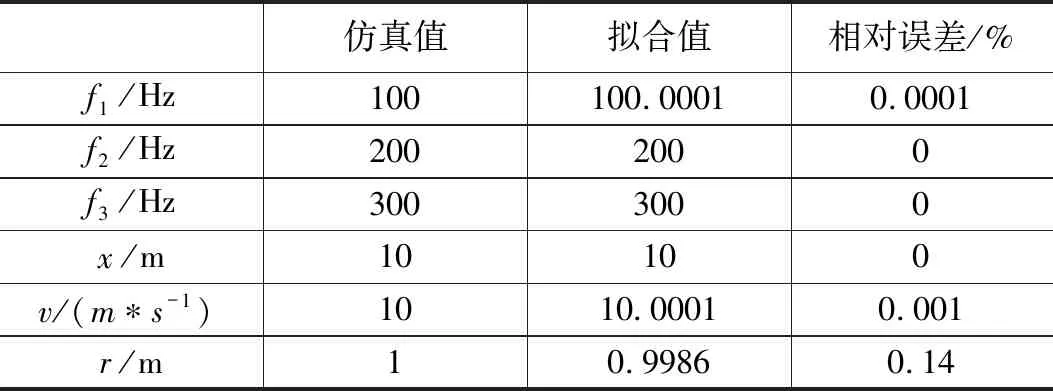
由于shannon熵在值为6.5处发生突变且大多数信号序列的shannon熵值大于6.5，因此选取shannon熵大于6.5的数据点。得到瞬时频率后，进行非线性最小二乘法拟合，其瞬时频率拟合图如图8 所示。拟合函数中有6个未知量，即f1，f2，f3，r，v，x。如表1为将仿真参数值与拟合值的相对误差。

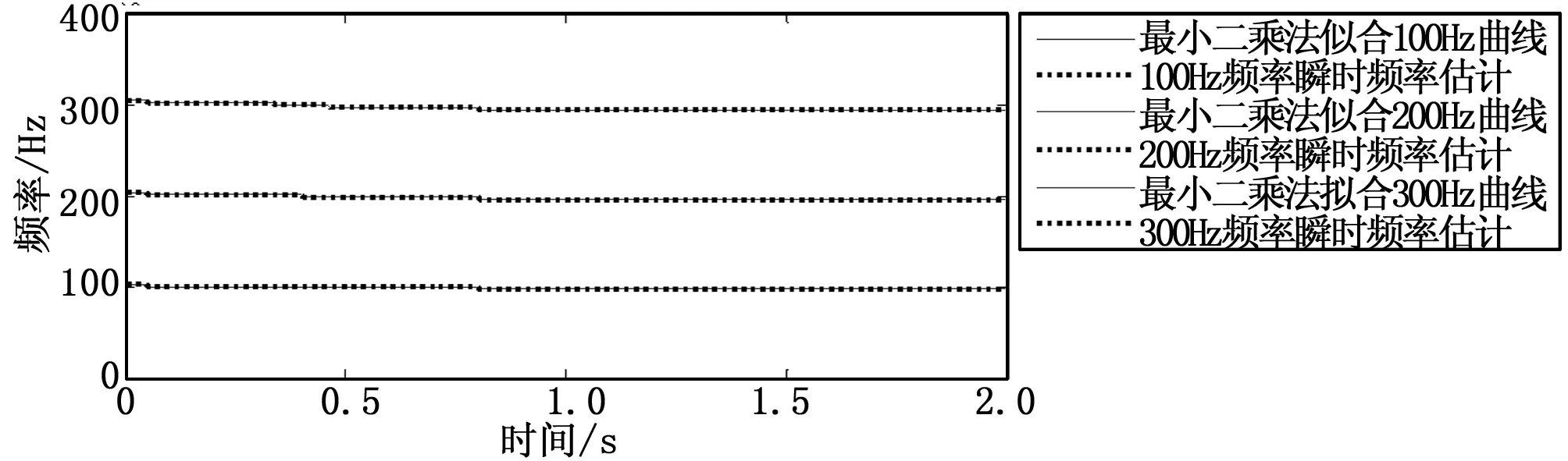
图8 瞬时频率拟合图

仿真值拟合值相对误差/%f1/Hz100100.00010.0001f2/Hz2002000f3/Hz3003000x/m10100v/(m∗s-1)1010.00010.001r/m10.99860.14

最后，采用本文提出的信号畸变校正方法。由图9和图10所示，可以清晰地看出，所设置的频率均得到了还原，而且从表1可以看出各参数的误差均很小，都在误差范围之内，从而验证了本文所提出的多普勒畸变校正方法的可行性。

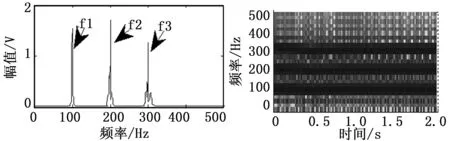
图9 重采样后频域图 图10 重采样后的STFT图

4 试验验证

为有效验证本文方法的可行性，本文利用电动车运载声源形成多普勒效应。如图11(a)所示，声源是利用录音笔从轴承型号为SKF 6016的试验台录制而成，设置静止实验台轴的转速为114 r/min(对应实际车辆36 km/h车速)。实验台所用的滚动轴承的内径为80 mm,外径为125 mm，滚子直径为14 mm，滚子个数为14，接触角为0°，轴承宽度为22 mm。

根据轴承故障特征频率计算公式，可以得出理论的内圈故障特征频率应为15.1 Hz。具体计算的内圈故障特征特征频率及倍频见表2。

表2 滚动轴承内圈故障特征频率及倍频

如图11(b)所示，电动车以36 km/h的速度匀速行驶，在前车轮处固定一录音笔，以播放轴承故障声音信号。数据采集设备型号为INV3060V，采集软件为DASP-V10，采样频率为10.24 kHz，采样时间为5 s，传声器与电动车行驶方向垂直距离大约 1 m 左右。由于故障特征频率三倍频都小于50 Hz，因此本文在频域图中分析的频率范围为[0 50]。为了更好地分析信号，本文只分析传声器前后1 s采集的信号。

图11 试验场景

图12采集到的轴承内圈故障信号。在频域图中，可以观察出在内圈特征频率15.1 Hz附近出现了一个1 Hz的频带展拓。而在图13(a)无法观察到15.1 Hz频率，因此从图12和图13(a)可以说明采集到的信号发生了多普勒畸变。图13(b)为信号序列分为512段的shannon熵值。由于shannon熵值为4.5时信号序列突变并且大多数信号序列的shannon熵值大于4.5，因此设置shannon熵的阈值为4.5。采用本文的瞬时频率进行频率估计，如图13(c)。

图12 采集到的轴承内圈故障信号

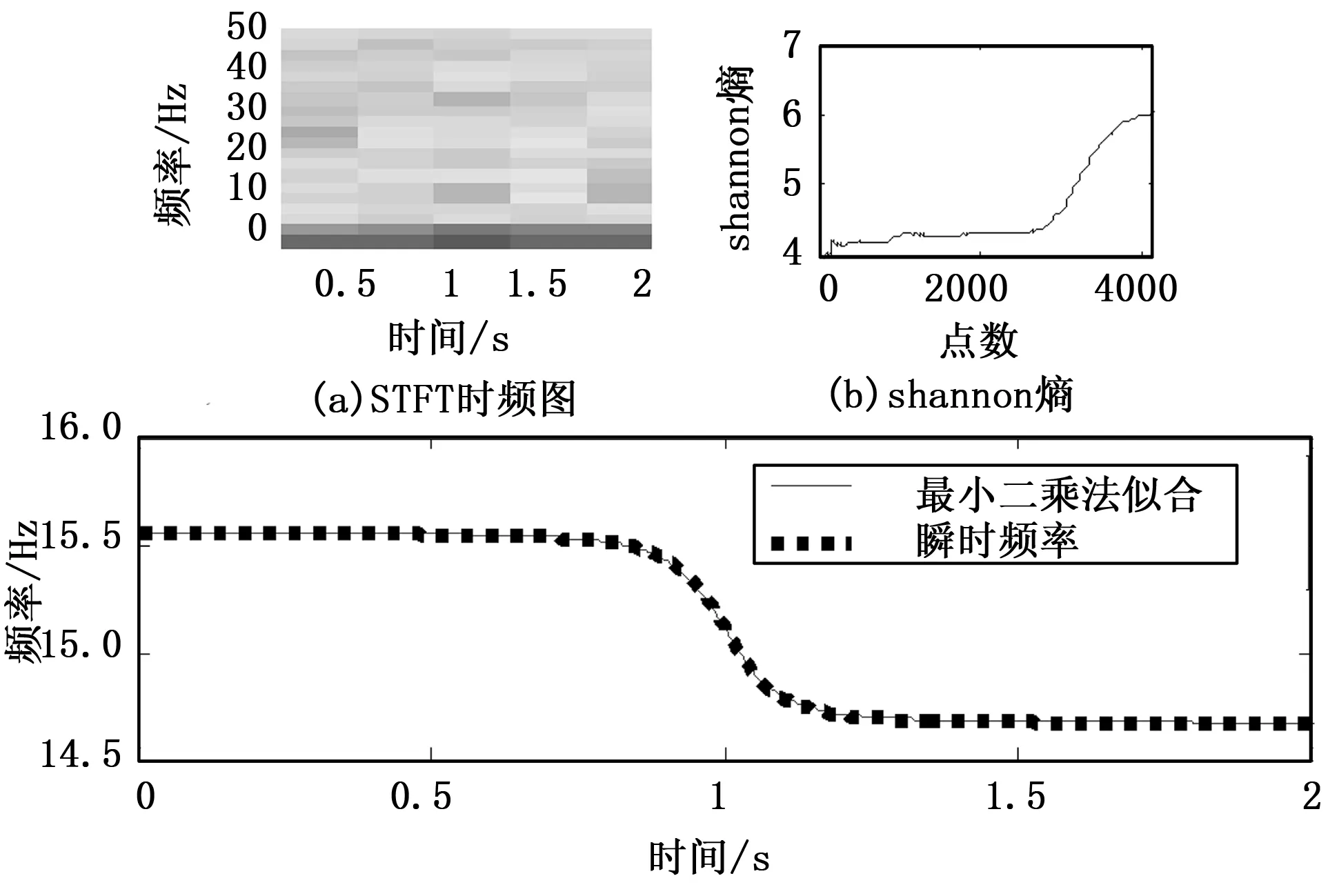
图13 瞬时频率估计

在图14(a) 中可以观察到校正后的信号频谱中出现了内圈故障频率15.1 Hz，1 Hz的频带展拓基本消失，精确度较高。在图14(b)中也可以观察到在15.1 Hz附近存在一个不随时间变化的频率。因此信号处理结果表明内圈故障频率得到了校正，内圈故障多普勒畸变已经基本消除。

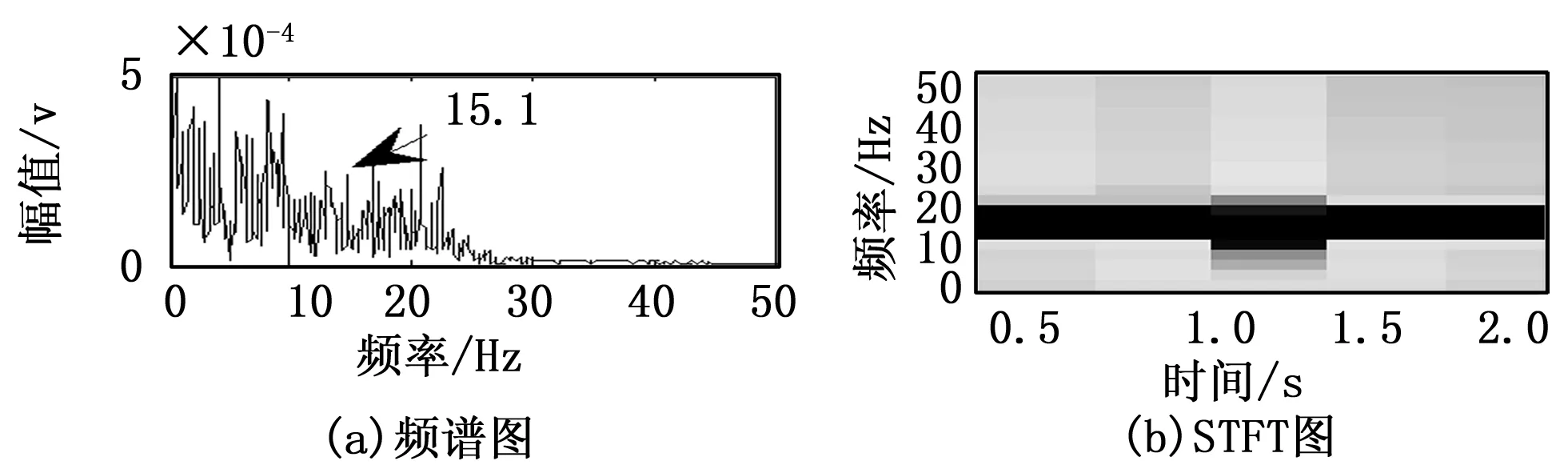
图14 轴承内圈故障信号重采样后信号分析

为了体现本文方法的优势，本文将其与传统STFT搜峰瞬时频率估计方法进行比较。设置传统STFT搜峰瞬时频率估计参数与本文方法参数一致。效果比较见图15及表3。从图15(a)可以观察到利用传统STFT搜峰瞬时频率估计方法还原的频率为15 Hz,在图15(b)中的1 s到1.5 s之间15 Hz频率的频带发生了错位，因此精确度一般。从表3可以看出，本文所用方法在瞬时频率用时、自适应性及准确度方面都具有一定的优势。

图15 传统方法的轴承内圈故障信号重采样后信号分析

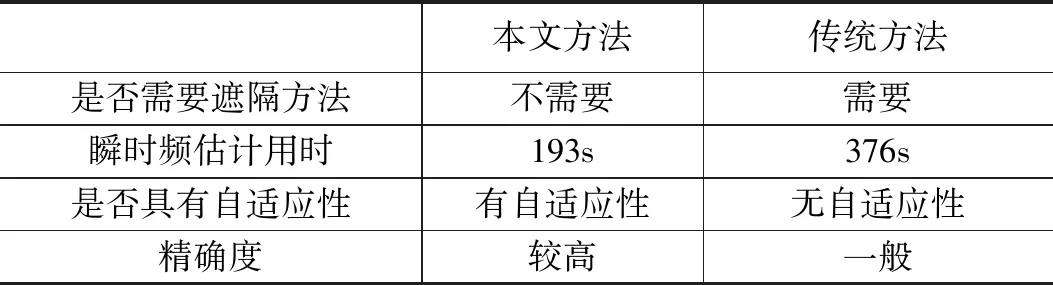
本文方法传统方法是否需要遮隔方法不需要需要瞬时频估计用时193s376s是否具有自适应性有自适应性无自适应性精确度较高一般

5 结束语

本文提出一种基于自动搜峰和shannon熵的滚动轴承多普勒畸变故障声信号校正方法。通过对仿真信号分析，可以看出该方法的误差在容许的范围内。通过试验结果分析，重采样后的内圈故障信号频谱中出现了内圈故障特征频率，在重采样后的STFT图中也可以观察到内圈故障频率得到了校正。因此该方法可应用于基于道旁声学的车辆轴承故障诊断中。同时与传统STFT搜峰瞬时频率估计方法相比，本文所用方法在瞬时频率用时、自适应性及精确度方面都具有一定的优势。