运输机标模CHN-T1的验证确认计算研究
2019-05-08章锦威张小亮孙晓玲戚淑妮
章锦威, 张小亮, 孙晓玲, 戚淑妮
(中国航空工业空气动力研究院, 沈阳 110034)
0 引 言
阻力高精度计算是民用飞机设计中计算流体力学仿真的主要研究方面,也是飞行器外形气动特性分析中非常关注的问题。为了系统评估CFD计算阻力的发展水平,国际上先后组织了许多专题研讨会,比如美国AIAA应用空气动力学会委员1998年成立了CFD阻力预测工作小组DPW(Drag Prediction Workshop),已于2001年开始召开了六次阻力预测会议[1-6]。NASA还专门发布了NPARC Alliance CFD验证与确认档案官方网站[7]。近年来,国内的科研单位[8-9]也陆续地开展了有关国际标模验证和确认的研究工作,初步设计了验证和确认共享数据库,并利用这些数据资源进行了航空CFD的验证与确认工作。邓小刚[10]等对国内外CFD验证与确认的发展情况,并对CFD软件的可信度分析工作提出了若干建议。陈树生[11]等针对大型CFD软件的验证和确认,专门开发了具有标准共享的专业数据库,适用于CFD软件开发、测试、验证和评估等领域的自动化验证确认云平台。
总体而言,国内相关活动缺乏完整性,且试验模型与试验数据基本采用国外数据,CFD分析不够深入。运输机标模CHN-T1是由中国空气动力研究与发展中心自主设计的一个跨声速运输机的典型算例,在FL-13风洞、DNW-LLF风洞进行了低速测力试验,在FL-26风洞、ETW风洞进行了高速测力试验,具有比较丰富可靠的试验数据[12]。
本文采用自研的非结构混合网格解算器CARIA-OVERSET对运输机标模CHN-T1进行了验证确认计算研究。根据第一届航空CFD可信度研讨会-CHN-T1标模CFD可信度研讨会活动要求,对运输机标模CHN-T1开展了网格收敛性研究和计算精度研究。主要研究了网格形式、网格尺度、模拟条件等对运输机标模CHN-T1的总体气动特性、局部流场特征、压力分布以及计算收敛性等的影响。
1 数值方法
本文的流场计算主要采用中国航空工业空气 动力研究院自主研发的航空数值计算平台CARIA_OVERSET,该平台采用非结构网格技术和基于对偶网格的有限体积方法,以EULER方程或NS方程加湍流模型作为主控方程,用于求解定常和非定常流动的流场。无黏通量差分格式包括通量矢量分裂和通量差分分裂格式,其离散格式主要有完全迎风格式、Frommer格式、中心格式和二阶迎风偏置格式。在时间推进方面,采用隐式近似因子分解迭代方法,其中定常流动采用一阶格式,非定常流动则采用隐式双时间步长方法,并通过隐式残值光顺和多重网格等技术加速收敛,缩短计算时间。
此外,CARIA_OVERSET包含丰富的湍流模型:零方程的Baldwin-Lomax模型,一方程的Baldwin-Barth、Spalart-Allmaras模型,两方程的Wilcoxk-ω、SST、k-ε等十几种湍流模型,以及丰富的可用于各种航空专业领域的计算边界条件。另外,CARIA_OVERSET中包含了eN方法、γ-θ转捩模型方法和固定转捩预测方法等,能够实现对不同转捩机理作用下的转捩问题的准确预测。
在本文计算中,对流项采用为二阶迎风Roe格式进行离散,二阶重构采用的梯度方法为节点型Gauss方法。黏性项采用中心差分离散。时间推进方法为隐式的LU-SGS方法,采用为二重“V”循环多重网格加速收敛,全局CFL数设置为1。计算假定流场为完全湍流流场,湍流模型主要采用一方程Spalart-Allmaras模型、两方程的Wilcoxk-ω和SST模型。计算主要采用百核分区并行计算,迭代步数10 000步~20 000步之间。
γ-θ模型求解两个变量的标准输运方程:
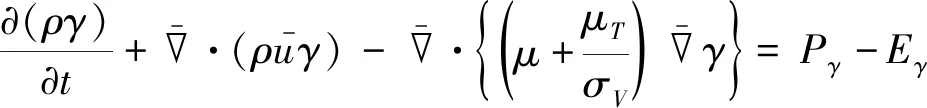


2 计算外形和网格
运输机CHN-T1标模采用类似波音737、空客320、C919等飞机的布局形式,即窄体机身、下单翼形式的超临界机翼和平尾、单立尾、翼吊式发动机布局。CHN-T1标模选取面积95.346 m2、展弦比9.3、梢根比0.298、1/4弦线后掠角25°的机翼设计参数、巡航马赫数为0.78,巡航升力系数为0.5。该模型几何尺寸合理,有利于开展风洞试验模型设计加工和CFD计算的网格制作,可为各种CFD软件代码提供验证计算的标准算例, 其详细参数可见文献[15]。本文主要针对运输机标模CHN-T1进行了验证确认计算研究,该模型的几何特征参数见表1。
本文的网格收敛性研究,主要采用中国空气动力研究与发展中心提供的官网网格和自研网格。官网网格包括粗中细不同尺度的非结构混合网格[16]和结构多块网格[17],其中粗、细结构多块网格是以中等网格为基准自主生成,网格生成参考组委会提供的网格生成标准和规范。网格具体信息参见表2,不同类型、中等尺度表面网格参见图1。

表1 几何特征参数Table 1 Geometric characteristic parameters
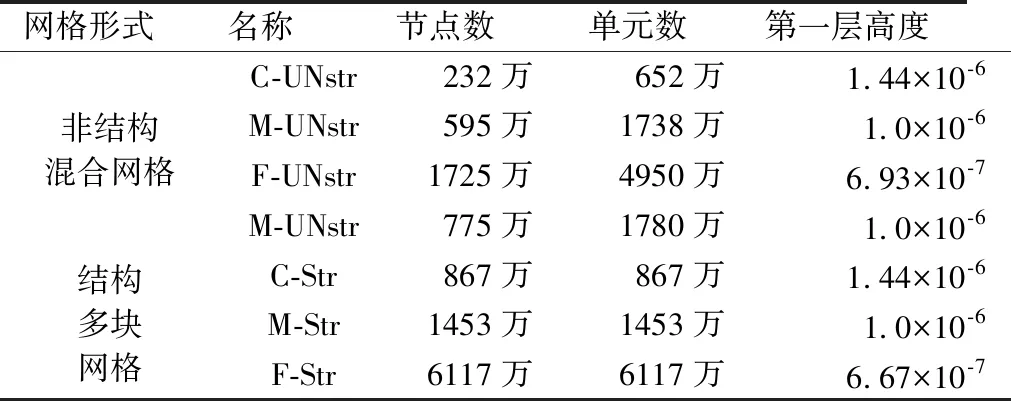
表2 网格信息说明Table 2 Grid information description

图1 不同类型、中等尺度计算网格示意图Fig.1 Schematic diagram of different grid types
3 计算状态介绍
计算状态主要包括三组研究案例,分别为网格收敛性研究、支撑机构及静气弹变形影响研究和雷诺数及转捩影响研究,具体计算状态参见表3。

表3 计算状态说明Table 3 Calculation status specification
4 数值仿真结果分析
4.1 计算收敛历程曲线
图2是解的收敛历史曲线。本文的气动力收敛原则,保证最后1000步升力系数波动幅值小于0.001,阻力系数波动幅值小于0.0001,俯仰力矩系数波动幅值小于0.001。由图可以看出,在保证气动力收敛准则的前提下,所有状态的密度残差都下降了5个以上量级,网格尺度越小,收敛速度越慢。

(a) 非结构混合网格
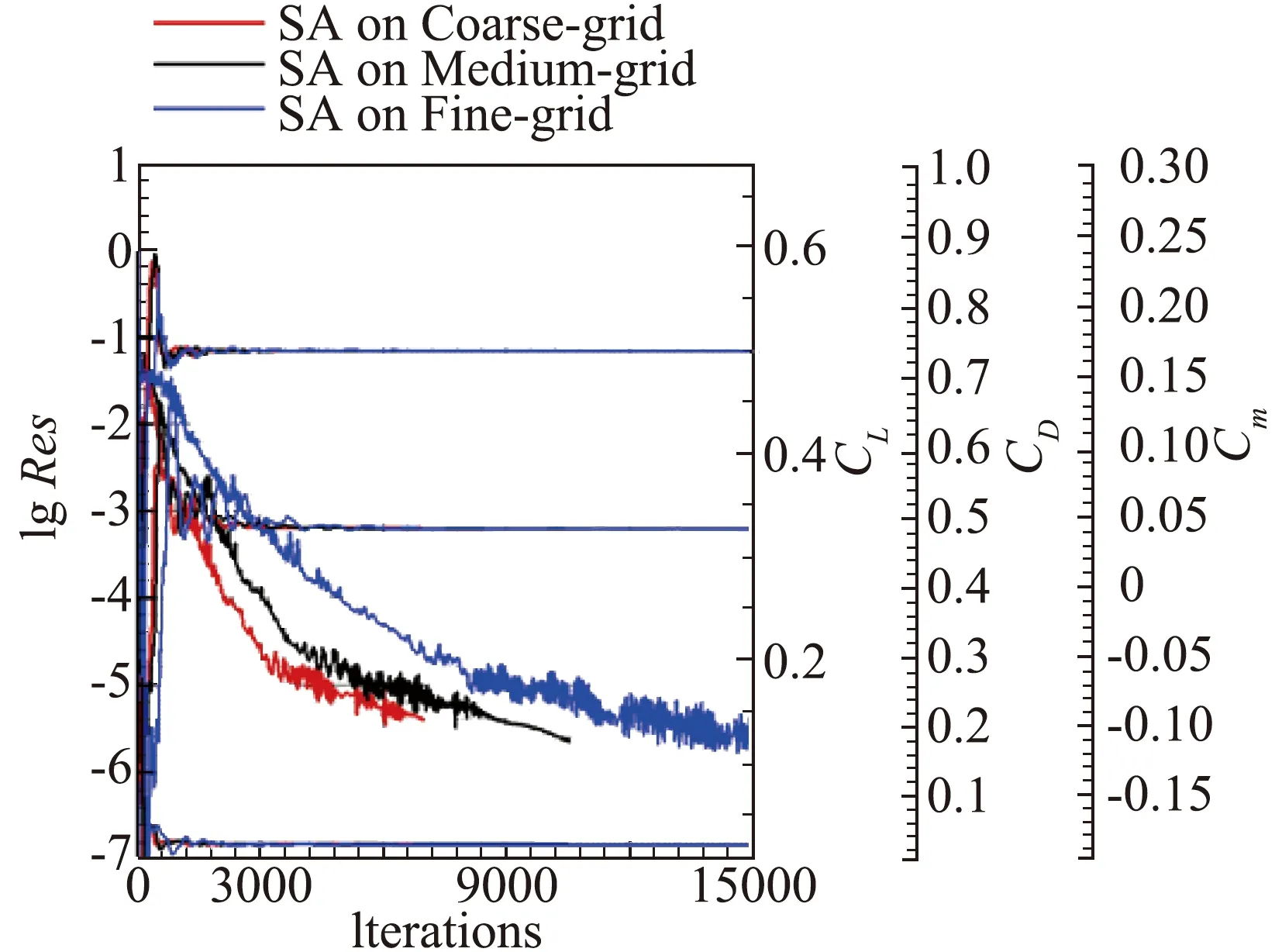
(b) 结构网格
4.2 网格尺度影响分析
为了进行网格收敛性的分析,至少要进行三个不同网格尺度的计算,获得S1(细)、S2(中)和S3(粗)三个解,它们之间的差及其比率R为:
R=ε21/ε32(3)
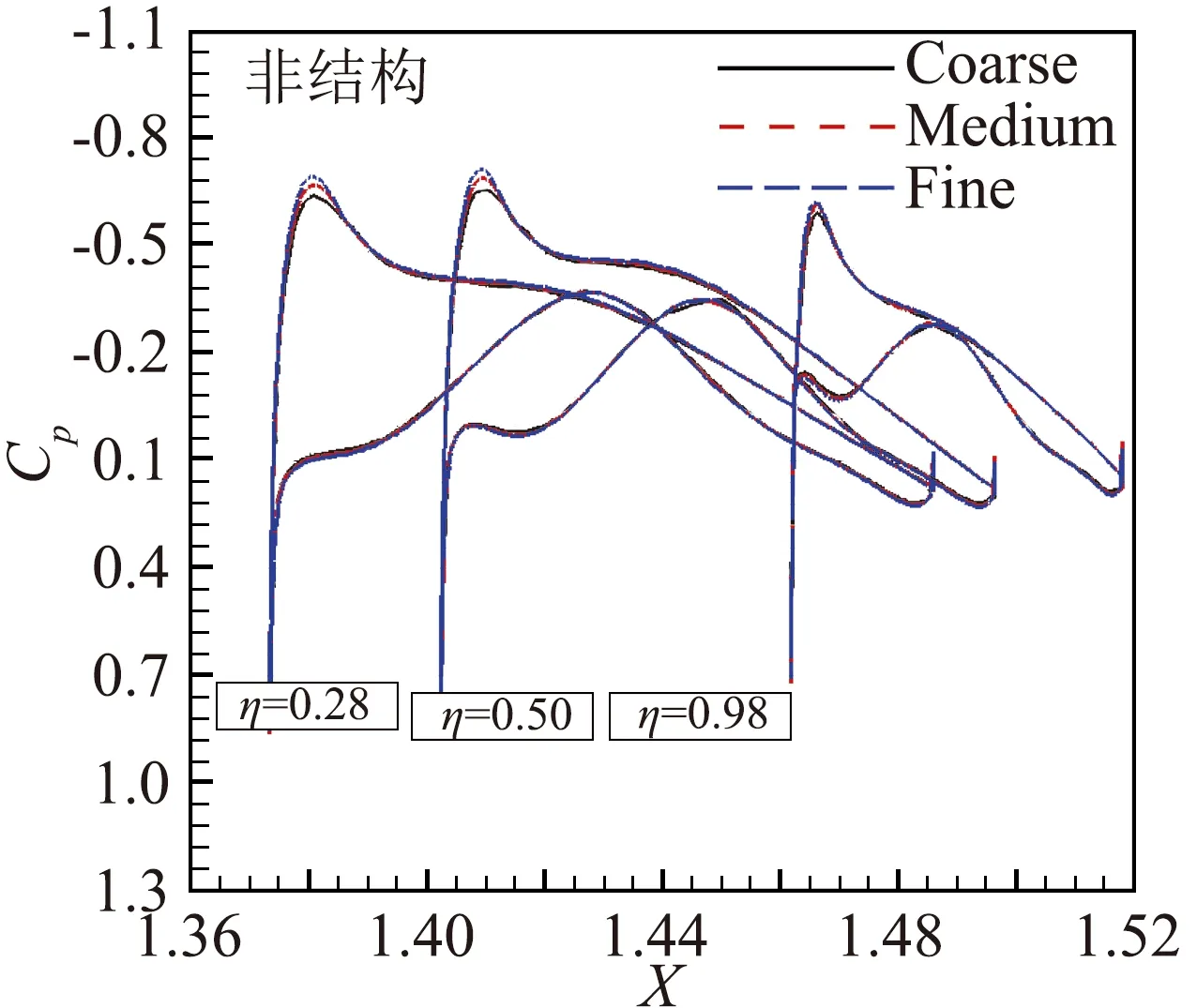
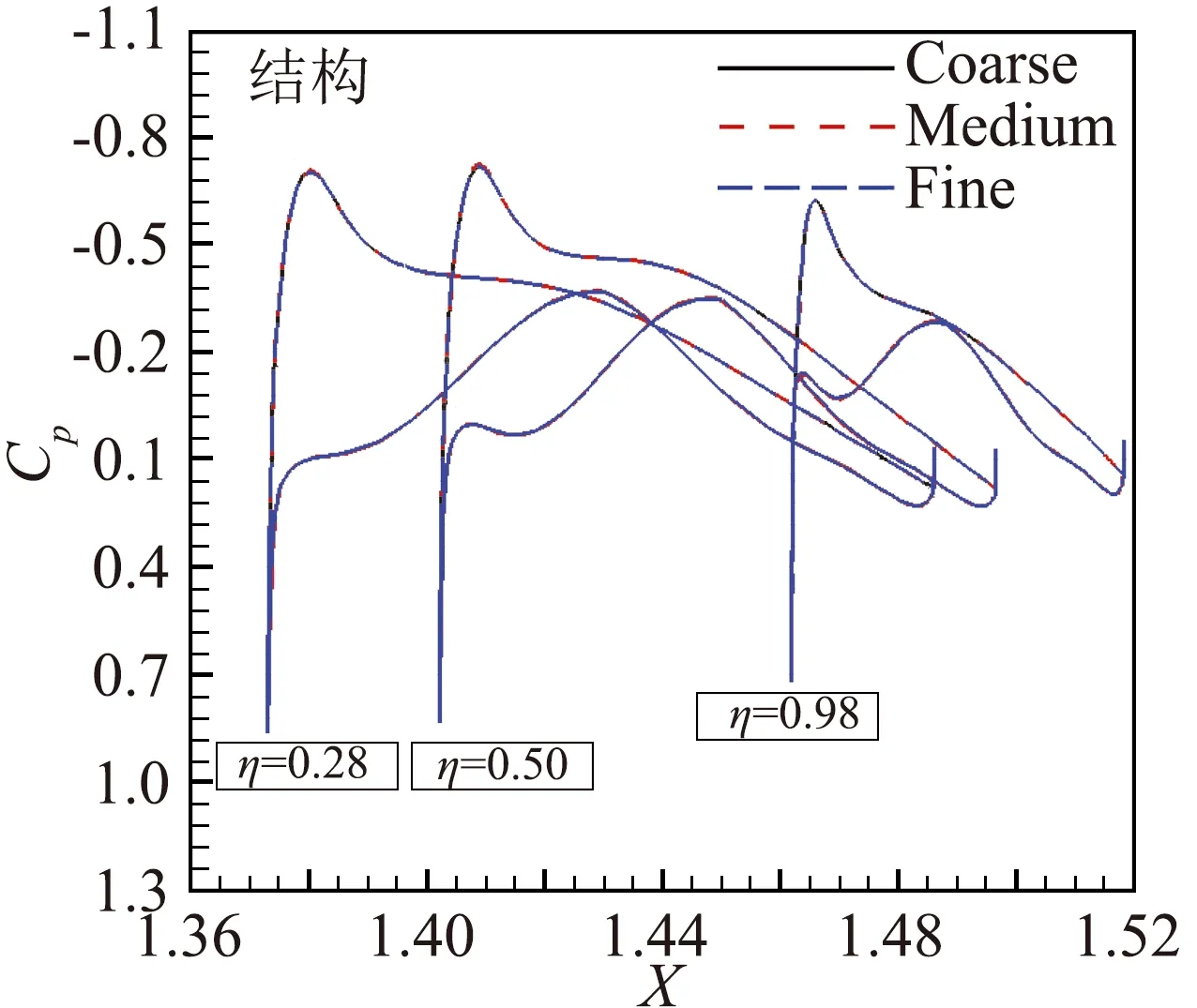
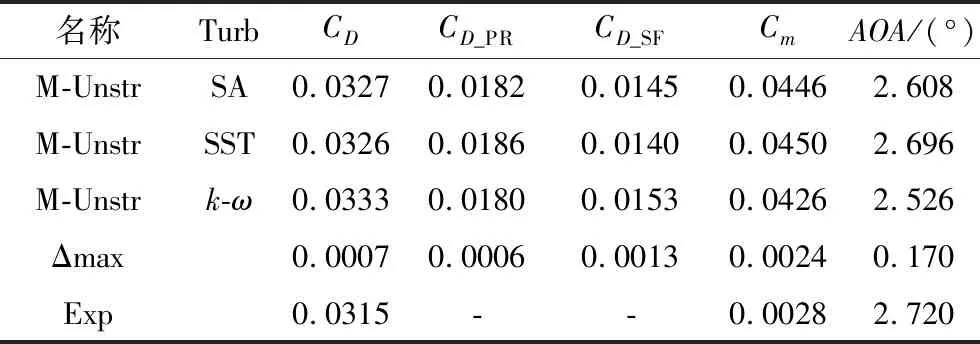
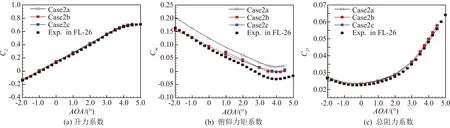
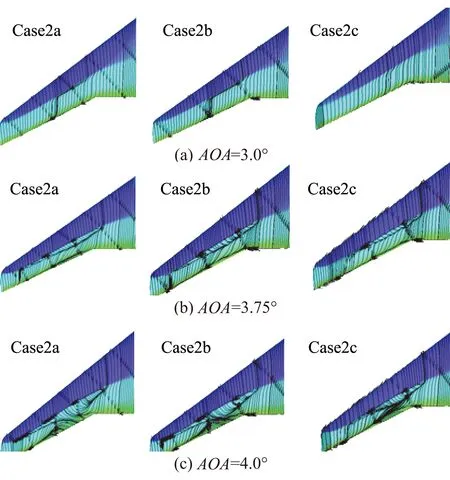
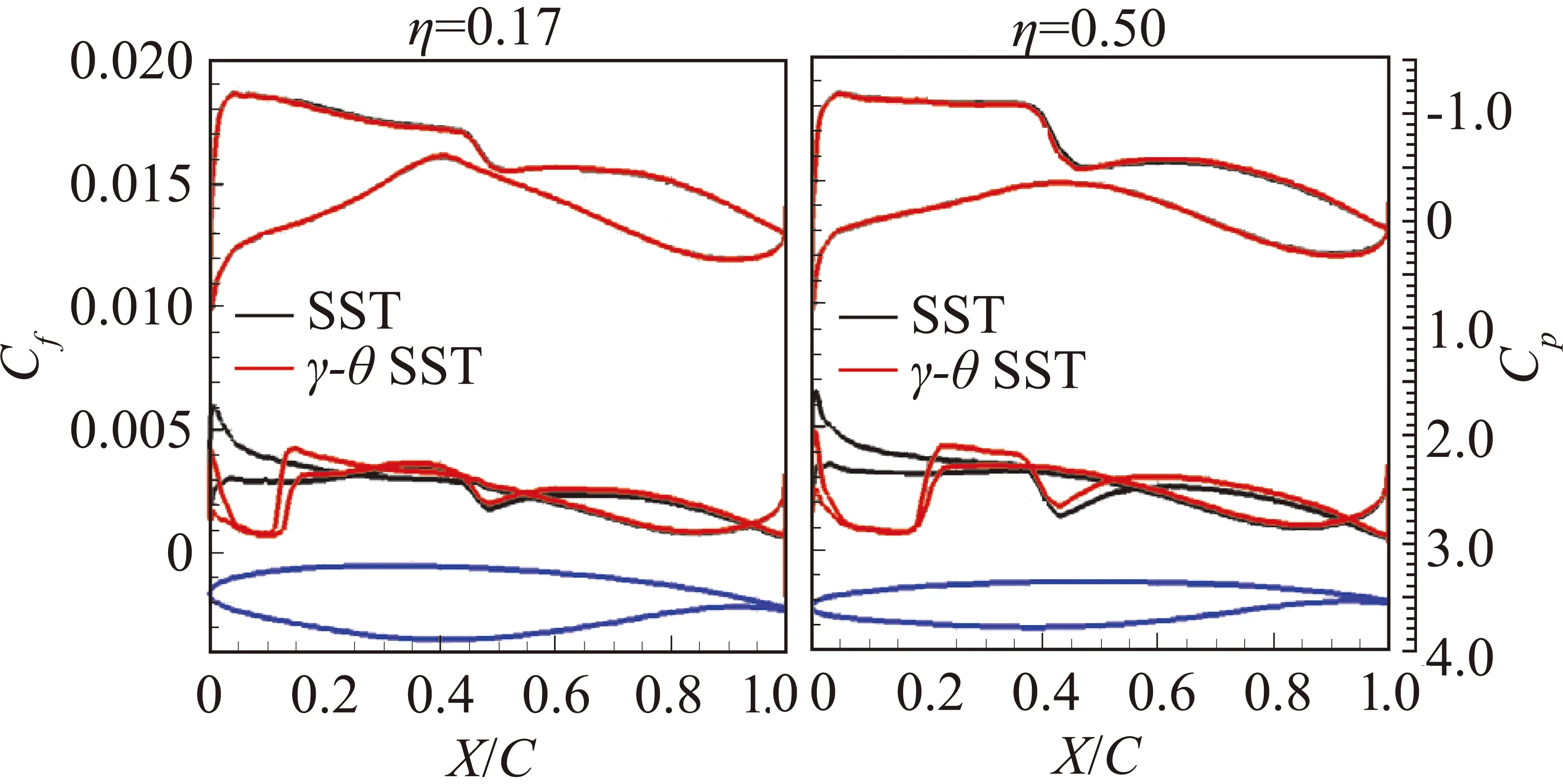
网格收敛性条件为:0 为了展示网格密度对误差估计计算结果的影响,本文对不同网格形式的粗中细各三套网格进行收敛性分析,分析的数据分别是阻力系数CD、压差阻力CD_PR、摩擦阻力CD_SF、俯仰力矩系数Cm和修正值。其中,网格误差δ*(广义Richardson外推法,忽略高阶项的影响) 和修正值SC相关的计算公式为: SC=S1-δ*(6) 式(4)、(5)中,r为不同网格尺度间的比值,本文取值为1.44。 图3给出的是不同形式网格计算所得气动力系数随网格数量变化对比曲线,其中,N为网格节点数。由图可以看出,非结构混合网格和结构网格均有一定的网格收敛趋势,且非结构混合网格的收敛趋势更明显。 (a) 迎角和俯仰力矩 (b) 总阻力、压差阻力及摩擦阻力 表4是在Ma=0.78、CL=0.500±0.001时,不同形式、不同尺度网格计算所得的气动力、力矩以及部分试验数据。可以看出,在固定升力条件下,计算迎角普遍小于试验迎角;网格尺度对摩擦阻力和压差阻力均有一定影响,摩擦阻力差量为2 counts(非结构混合网格)和0.7 counts(结构网格),压差阻力差量为31 counts(非结构混合网格)和6 counts(结构网格);在固定升力条件下,不同的网格尺度对力矩系数影响较小,计算得到的抬头力矩普遍大于试验结果。 依据网格收敛性条件要求,非结构混合网格计算所得气动力系数均为单调收敛,可以采用Richardson外推法初步估算,而结构网格计算所得俯仰力矩系数为震荡收敛,只能得到其误差范围,而其它气动力系数均发散,误差和不确定度均不能进行估算。非结构混合网格采用Richardson外推法初步估算所得各项气动力参数与结构网格线性插值计算结果接近,与文献[17]提供的104亿网格相比,除迎角存在一定差异外,其余结果接近。 表4 网格收敛性分析Table 4 Grid convergence analysis 图4~图5给出的是机翼和平尾不同展向站位及对应压力分布情况对比。由图可以看出,非结构混合网格计算所得机翼内侧站位的Cp分布差异较小,差异由内向外逐渐增大,网格尺度越大,激波位置和强度的捕捉越精确,平尾内侧站位的吸力峰值差异明显。结构多块网格计算所得机翼和平尾不同展向站位的Cp分布差异较小。以上结果与前文所得气动力系数分析结论一致。 图4 机翼及平尾展向站位示意图Fig.4 Schematic diagram of wing and tail deployment position 图6给出的是固定升力条件下,非结构混合网格采用不同网格尺度计算所得翼身结合处分离流场结果。由图可以看出,在上述来流条件下,翼身结合处产生了很小的分离区,除粗网格模拟结果存在差异外,中细不同网格尺度在翼身结合处局部分离流的模拟上结果接近。 (a) 机翼 (b) 平尾 图6 翼身结合处上表面流线(不同网格尺度)Fig.6 Upper surface streamline near wing body junction(different grid scales) 表5是在Ma=0.78、CL=0.500±0.001时,采用一方程的Spalart-Allmaras模型,两方程的Wilcoxk-ω、SST共计三种湍流网格计算所得的气动力、力矩以及部分试验数据。可以看到,基于同一套非结构混合网格,采用不同湍流模型计算所得结果存在一定差异,SA和SST两种湍流模型的计算结果较为接近,SST计算所得阻力和迎角与试验结果更加接近。 表5 湍流模型对气动力的影响分析Table 5 Influence of turbulence models on aerodynamic forces 图7给出的是固定升力条件下,非结构混合网格不同湍流模型计算所得翼身结合处分离流场结果。由图可以看出,在上述来流条件下,翼身结合处均产生了较小的分离区,不同湍流模型计算所得机翼弦向、展向分离边界位置以及机身的分离泡中心、鞍点位置等均非常接近。 图8(a~c)分别给出了干净模型、带支撑机构模型和静气弹变形机翼带支撑机构模型计算所得全机的升力、俯仰力矩以及总阻力系数对比曲线。由图可以看出,本文方法计算所得全机升阻力系数与试验数据吻合度较好,俯仰力矩曲线规律与试验数据较为相似。在本文计算条件下,不同构型计算所得全机升阻力系数及俯仰力矩系数有不同程度变化: (1) 带支撑机构模型相比干净模型,升力系数最大增加0.0172,阻力系数最多减小9 counts(压差阻力-6.5 counts和摩擦阻力-2.4 counts),最大升阻比增加1,低头力矩系数最大增加0.0487; (2) 静气弹变形机翼带支撑机构模型相比干净模型,升力系数最多减小0.0092,阻力系数最多减小22.5 counts(压差阻力-23.5 counts和摩擦阻力+1 counts),最大升阻比增加0.1, 低头力矩系数最多减小0.008 53。 图9~图10给出了当AOA=3.75°时,干净模型、带支撑机构模型和静气弹变形机翼带支撑机构模型计算所得机翼和平尾不同展向站位Cp分布曲线。由图可以看出,支撑机构主要影响平尾(与支撑方式有关),支撑机构导致截面Cp环量减小,且越靠内侧影响越大;静气弹变形主要影响机翼,静气弹变形机翼上表面吸力减小,激波位置前移,且越靠外侧影响越大。 图8 不同构型计算所得全机气动力系数曲线Fig.8 Aerodynamic coefficient curves calculated by different configurations 图9 AOA=3.75°,机翼不同展向站位Cp分布变化对比Fig.9 Comparison of Cp distribution at different wing deployment stations and AOA=3.75° 图11~图12给出了不同迎角条件下,机翼上表面流线分布及展向中间站位Cp分布曲线。当迎角AOA从3°增加到3.75°时,激波位置后移,翼中激波位置附近开始出现分离;当迎角AOA从3.75°增加到4.25°时,激波位置前移,机翼后缘分离位置迅速前 移。激波位置的变化引起局部流动分离特征的变化,这是诱发跨声速机翼抖振问题的主要因素。 图11 不同迎角下,不同构型计算所得机翼表面流线对比Fig.11 Comparison of wing surface streamlines calculated from different configurations at different angles of attack 图12 不同迎角下,η=0.50机翼展向站位的Cp分布对比Fig.12 Comparison of Cp distribution at η=0.50 wing deployment station and different angles of attack 表6给出了不同模拟条件计算所得各项气动参数及其差量值。可以看出,雷诺数从330万增加到1500万,全湍模拟计算所得全机总阻力减小48 counts(压差阻力减小20 counts、摩擦阻力减小28 counts)迎角减小0.249°,抬头力矩增加0.0149;自由转捩模型计算所得全机总阻力减小16 counts(压差阻力减小7 counts、摩擦阻力减小9 counts),迎角减小0.053°,抬头力矩增加0.0176。全湍计算结果与试验结果更接近,自由转捩模型计算所得差量偏小。 图13~图15给出了全湍及自由转捩模型计算所得表面Cf分布云图、机翼不同展向站位Cp及Cf曲线。可以看出,雷诺数越大,转捩位置越靠前,全湍与自由转捩模型计算结果的差异越小,这与上文所得气动力变化规律一致。在固定升力条件下,机翼不同展向站位Cp曲线差异小。 表6 CL=0.500,不同模拟条件计算所得气动力差量对比Table 6 CL=0.500, aerodynamic coefficients calculated from different simulation conditions 图13 不同模拟条件计算所得机翼表面Cf分布云图对比Fig.13 Comparison of Cf distribution of wing surface calculated by different simulation conditions 图14 Re=3.30×106,不同模拟条件计算所得机翼不同站位Cf分布对比Fig.14 Re=3.30×106,Comparison of Cf distribution of different wing deployment stations calculated from different simulation conditions 图15 Re=1.50×107,不同模拟条件计算所得机翼不同站位Cf分布对比Fig.15 Re=1.50×107,Comparison of Cf distribution of different wing deployment stations calculated from different simulation conditions 按照第一届航空CFD可信度研讨会-CHN-T1标模CFD可信度研讨会活动要求,本文基于自研的非结构混合网格解算器CARIA-OVERSET对运输机标模CHN-T1进行了初步的验证确认计算研究,得到了以下基本结论: (1) 同等网格节点数量,非结构混合网格和结构多块网格计算所得气动力各项参数的差异很小。 (2) 对于网格尺度引起的误差,非结构混合网格大于结构多块网格,但非结构网格得到的修正值与结构网格接近,不同网格尺度对翼身结合处的分离特性模拟差异较小。 (3) 基于同一套网格,本文所采用的三种湍流模型计算结果表明,在固定升力条件下,湍流模型引起的摩擦阻力差量大于压差阻力,且对迎角和俯仰力矩的影响较大,翼身结合处的分离模拟差异较小。 (4) 带支撑构型的全机升力和低头力矩增加、阻力减小,力矩拐点提前,机翼静气弹变形后升力、阻力和低头力矩均减小,力矩拐点后移。全湍和自由转捩 模型的计算结果存在一定差异,但差异随着雷诺数的增大而变小。 本文计算分析所得大部分结论具有一定的参考价值,但也存在些许不足,特别是基于自由转捩模型的模拟计算,相关结论还需要更多可靠的试验数据作进一步的验证分析。
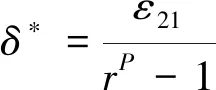







4.3 湍流模型影响分析
4.4 支撑机构及静气弹变形影响研究




4.5 雷诺数及转捩影响研究



5 结 论
