有局部稀薄气体效应的高超声速流动数值模拟
2019-05-08欧吉辉
欧吉辉, 赵 磊,2, 陈 杰,*
(1. 天津大学机械工程学院高速空气动力学研究室, 天津市现代工程力学重点实验室, 天津 300350;2. 中国空气动力研究与发展中心 超高速空气动力研究所, 绵阳 621000)
0 引 言
对于近空间高超声速飞行器,其飞行高度一般在40~70km高空,飞行速度一般在5~20倍声速范围内,随着飞行高度的增加,基于Navier-Stokes (N-S)方程的传统CFD方法逐渐失效,需要研究新的空气动力学问题[2]。近空间飞行的流场特点是,其边界层中温度很高,除迎风面压力较高外,其它部位的分子自由程会显著增大, 同时边界层中的剪切很强,因而会出现文献[1]中所考虑的那种稀薄气体效应。
对于存在局部稀薄效应的近空间高超声速飞行器流场模拟,现有的方法都存在一些局限,缺少模型可靠且计算量满足工程实际需求的方法[3-4]。Bird[5]提出的直接模拟蒙特卡洛方法(DSMC)被认为是稀薄气体流体动模拟方面最成功的方法之一,目前该方法已经可以用于模拟航天飞行器这类复杂三维外形的流场[6],并且可以考虑分子内能激发、电离、离解/复合化学反应、热辐射等复杂的物理化学变化[7-8]。但是,该方法将分子移动和碰撞解耦处理,要求计算网格小于分子的平均自由程、时间步长小于分子的平均碰撞时间,因此用于近连续流动时对计算资源提出了很高的要求。对于飞行高度在80km及以下的飞行器,计算量巨大,目前还无法应用于飞行器的设计上。Boltzmann方程虽然可以描述整个流域,但该方程是关于速度分布函数的七维积分微分方程,求解十分困难[9]。介于宏观与微观之间介观层次的格子Boltzmann方法(lattice Boltzmann method, LBM)被广泛用于模拟微尺度流动以及不可压缩流动[10-11]。作为LBM的一个变体,离散玻尔兹曼方法(discrete Boltzmann method, DBM)已经可以用于模拟可压缩化学反应流动[12]。不过这种方法在高超声速流动方面的工程应用前景有待进一步研究。最近我国学者在跨流域统一算法方面取得了重要进展[13-14],该算法将每个时间步长内宏观量的更新和微观气体分布函数的更新紧密地耦合在一起。但对于高速流动,离散速度对内存的需求以及计算成本高,限制了其在工程中的应用。另外发展起来的NS-DSMC耦和模型需要对流场分区,不同区域采用不同的计算模型和算法。但分区的判据带有一定的不确定性,分区计算界面处的数据交换也会限制计算效率的提升,已有文献报道NS-DSMC相比全DSMC的计算速度提升可达3倍左右[15-16],但这还不足以解决实际应用中DSMC和N-S在计算量上数量级的差别。
在CFD计算中,通过采用滑移边界条件可以将N-S方程的应用范围拓展到滑流区域[17-19]。但是随着稀薄程度进一步增加,N-S方程的线性本构关系逐渐失效,仅使用滑移边界条件不足以给出满意的结果。一方面,Lockerby[20]等基于均匀剪切流的线化Boltzmann方程的解提出了一个壁面函数,从而对努森层内的黏性系数进行修正,来考虑壁面附近努森层的影响。Lofthouse[17]等直接将该壁面函数纳入CFD滑移边界条件,并用于高超声速圆柱绕流计算,结果显示该方法取得的效果还比较有限。另一方面,在微槽道流的计算中,通过考虑壁面对分子运动的限制效果从而得到等效黏性系数以对传统的N-S本构关系进行修正[21-22]。然而,这种基于等效平均自由程的等效黏性系数的推导过程与几何模型密切相关,并且在推导过程中没有考虑空间密度的不均匀性,还不能直接用于高超声速流动计算。
陈杰和赵磊在文献[1]中,基于稀薄高超声速边界层流动特点,给出了一个判别气体稀薄效应大小的参数Zh,并采用DSMC对简单的平板剪切流进行了模拟分析。结果表明:由传统连续介质模型所计算的剪应力的误差随着Zh参数单调增大,继而由DSMC计算的剪应力在线性本构关系下所导出的等效黏性系数与传统的黏性系数之比随着Zh参数单调减小。据此,文献[1]提出,在流场存在局部稀薄效应的情况下可以根据流场的每一点的Zh值,对连续介质模型中的黏性系数加以修正,应该是一个既考虑了流场的局部气体稀薄效应,而又不显著增加计算的复杂性的办法。本文将以一个在70 km高空,以马赫数15飞行的小迎角平板为例,来检验上述方法是否可行。
1 计算模型
1.1 CFD模型
在本文中计算采用的方程为二维守恒型可压缩N-S方程,本构关系从形式上是线性关系,但在计算过程中,需要根据DSMC的结果对黏性系数进行修正。下面将这种修正N-S方程黏性系数的方法称为NS-VC (Navier-Stokes-Viscosity Correction) 方法,而黏性系数没有修正的则称NS方法。二维无量纲可压缩N-S方程为:
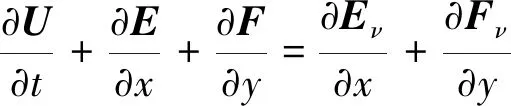
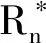
剪应力与热流计算式为:
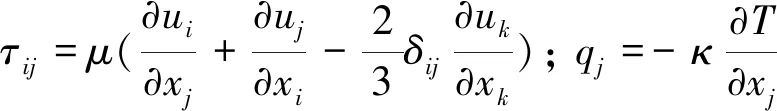
其中μ、κ分别为黏性系数与热传导系数,计算式为:
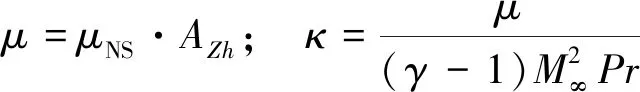
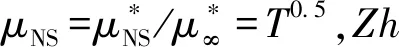
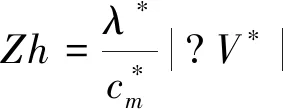
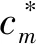
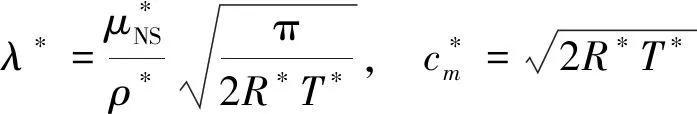
其中R*为气体常数,对于空气R*=287 J/(kg·K)。
陈杰等在文献[1]中通过DSMC对简单平板间均匀剪切流分析得到,由DSMC结果获得的等效黏性系数与传统连续介质模型中的黏性系数在连续流基本一致,但随着稀薄效应参数Zh的增大,二者之比会单调减小。两者之比,也是式(3)中黏性修正系数AZh,其与Zh参数的关系如图1所示。图中小黑点为文献[1]中所给结果,实线为由三次样条曲线拟合所得,以用于CFD计算。图1中DSMC的数据包含了不同壁面马赫数的工况,而不同工况槽道中心点的温度差别很大,因此图1的规律与温度无关。从气体的流变性质看,图1的规律体现出气体剪切变稀的性质,对于偏离平衡态比较远的强剪切流动,气体的等效黏性系数不再只与温度有关,而是随着剪切率的增加而逐渐减小。另外,虽然图1的结果只显示出了修正系数对Zh的依赖关系,但是Couette流同时也存在很大的温度梯度与热流,实际上图1的结果也包含着热流对黏性系数的影响。因此作为初步尝试,可以将图1的规律用于CFD计算看是否可以改进传统CFD的结果。
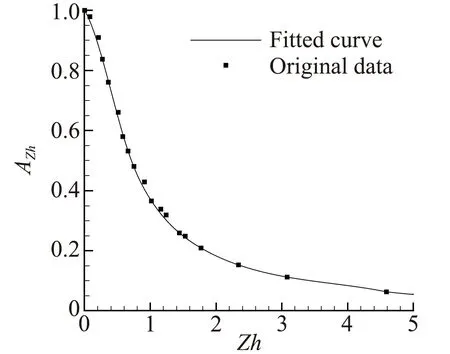
图1 黏性修正系数AZh随Zh数的变化 Fig.1 The relationship between AZh and Zh
1.2 计算模型与工况
计算模型为钝平板,模型示意图如图2所示,其中x、y分别为沿轴向以及垂直于轴向,坐标原点选在钝头圆心处。点A所示位置为钝平板前缘,ξ为从前缘沿壁面的贴体弧长,AOA为迎角,Rn为有量纲圆头半径。在下文中,迎风面以及下平板指的是流场或平板对应y<0的区域,背风面以及上平板指的是流场或平板对应y>0的区域。本文计算了不同迎角、不同球头半径下马赫数15、壁面温度为2000K的工况,具体参数在表1列出。来流为70 km高空气体,其物理参数为:
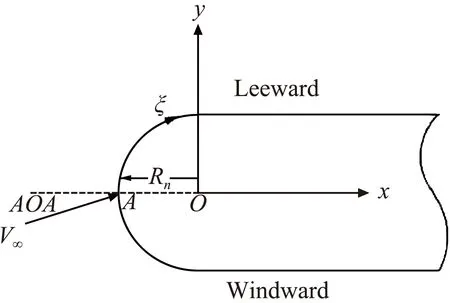
图2 计算模型示意图Fig.2 Sketch map of computation model
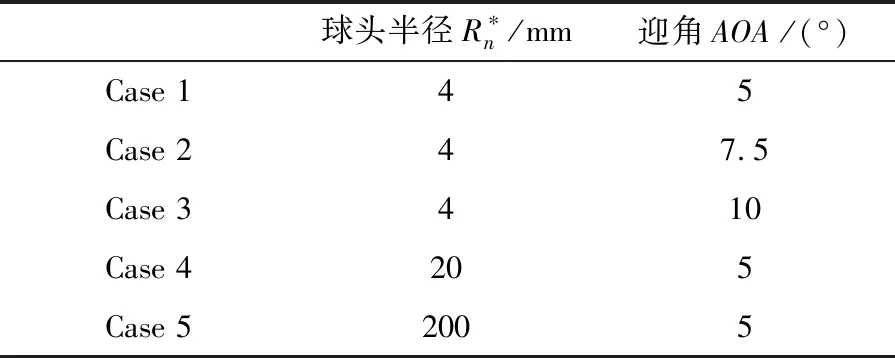
球头半径R∗n/mm迎角AOA /(°)Case 145Case 247.5Case 3410Case 4205Case 52005
1.3 数值方法
由于NS-VC方法只对N-S方程的黏性系数进行了修正,其方程形式与N-S方程并无本质区别,因此传统的CFD求解方法均有效。考虑到二阶NND[24](Non-oscillatory, No free parameter and Dissipative)格式具有无振荡捕捉激波、鲁棒性很好、计算效率高等优点,在本文计算中,对流项离散采用二阶NND格式,黏性项离散采用二阶中心差分,时间推进采用二阶Runge-Kutta法。为突出稀薄效应对黏性系数的影响,壁面没有采用滑移边界条件,而仍用无滑移等温条件。远场为来流条件,出口为外推边界条件。
对于高超声速稀薄流动,对黏性项的刻画至关重要。由此,在图3中给出了Case 1工况二阶NND格式与五阶WENO[25](Weighed Essentially Non-Oscillatory)格式(黏性项采用六阶中心差分)计算得到的壁面摩擦系数与速度剖面比较的结果。其中ξ为沿壁面弧长,壁面摩擦系数计算式为:
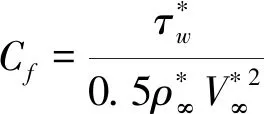
由图3可以看到,对于NND的计算结果,其背风面壁面摩擦系数和x*=1 m处速度剖面与五阶WENO的结果都吻合得很好。因此,在本文的计算工况中采用二阶NND格式可以很好的刻画黏性项,后面的计算都采用二阶NND格式进行计算。
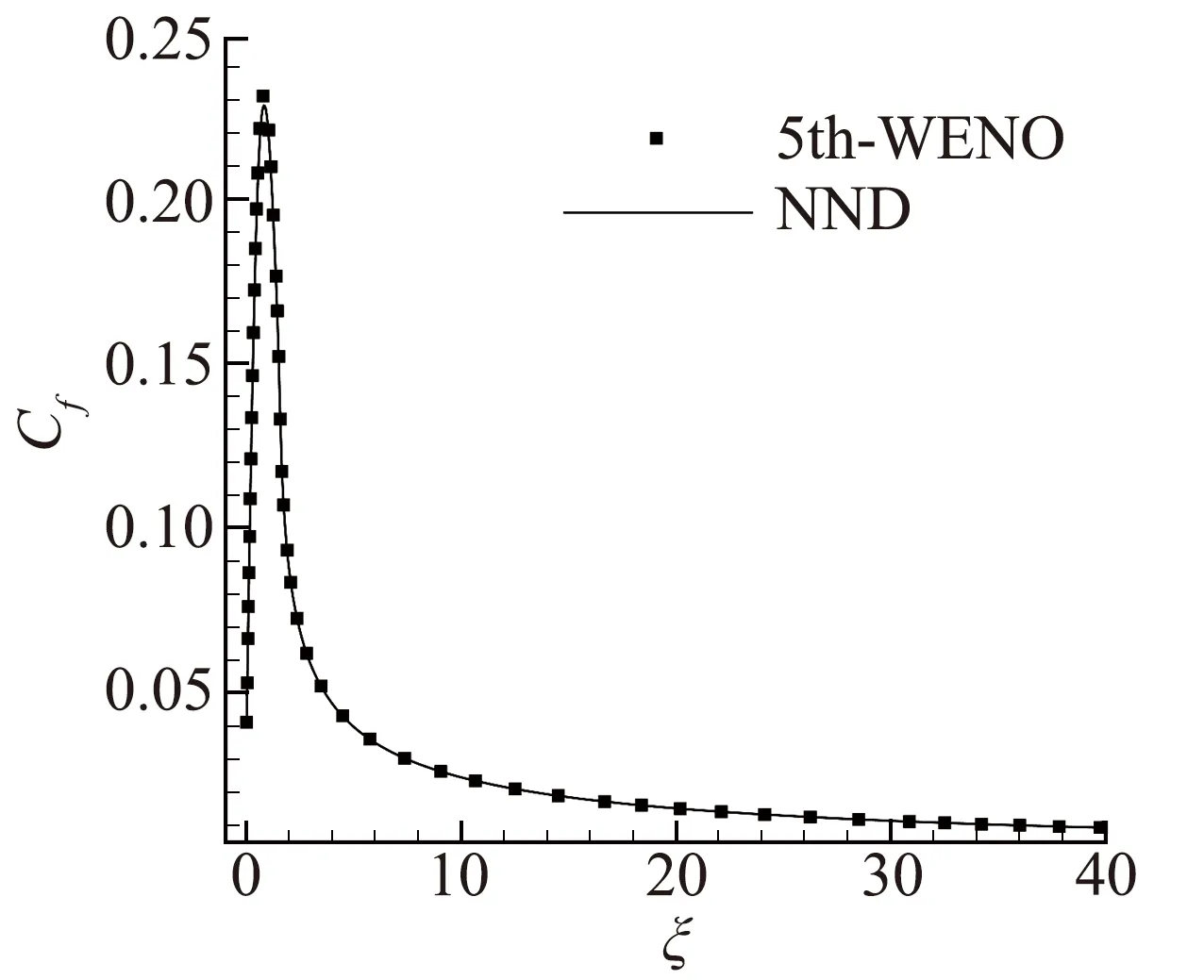
(a) 背风面壁面摩擦系数沿壁面的分布
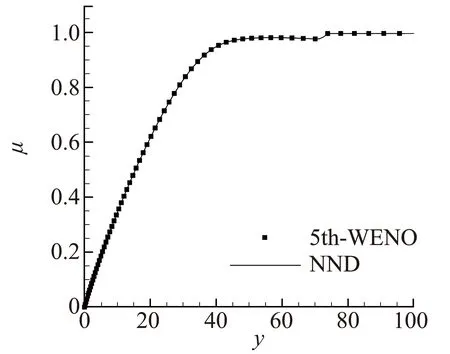
(b) 背风面x*=1 m处速度剖面
在CFD中实施黏性修正的具体计算过程为:先用NS方法计算一段时间(不需要等到收敛),然后切换到NS-VC方法,在每一时间步,根据当时的流场,计算每一点的Zh值,得到相应的AZh,据此修正每一点的黏性系数,沿时间推进直至收敛。
实际上,NS方法和NS-VC方法的差别仅在于后者在每一步迭代后,需对所得流场的每一网格点计算Zh值,并据之对该处的黏性系数做修正,因此每一迭代步所需时间要增加约17%。此外,在启动计算时,由于整个流场是从静止态开始,而边界条件则是给定值,所以在局部地方的剪切率会非常大,从而相应地该处的Zh值也很大,超出了可知的范围而无法运行。因此要先用NS方法计算一段时间后,才能切换到NS-VC方法上来。这样,总的迭代步数也会增加一些。对我们的算例,所需总的计算时间比单纯用NS方法计算时约多50%左右。
2 结果及分析
2.1 黏性修正的影响
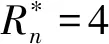
图4给出的是用NS方法计算得到的Zh值在空间分布的等值线图。可以看到,Zh值比较大的地方主要集中在激波、头部和背风面壁面附近,说明这些位置是流动中稀薄效应最强的区域。图5(a)给出的是NS方法计算得到的Zh值在背风面和迎风面沿壁面的分布。可以看到Zh值都是先增大后减小,在平板圆头与板身相接的位置取得最大值。图5(b)给出的是NS-VC计算收敛时背风面与迎风面壁面修正系数沿流向的分布。与图5(a)中Zh值变化趋势相反,黏性修正系数先减小后增大,在平板圆头与板身相接处最小。这是由于Zh值越大,表征稀薄效应越强,因此黏性修正得越多。对于ξ>100,背风面黏性修正系数介于0.7与0.8之间,即修正后的等效黏性系数为原来黏性系数的70%~80%。迎风面的Zh值比背风面的小很多,因此对黏性系数的修正量也很小。
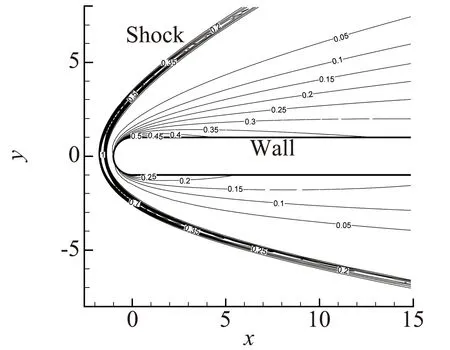
图4 NS: Zh值空间分布的等值线图Fig.4 Contour map of Zh value in spatial distribution
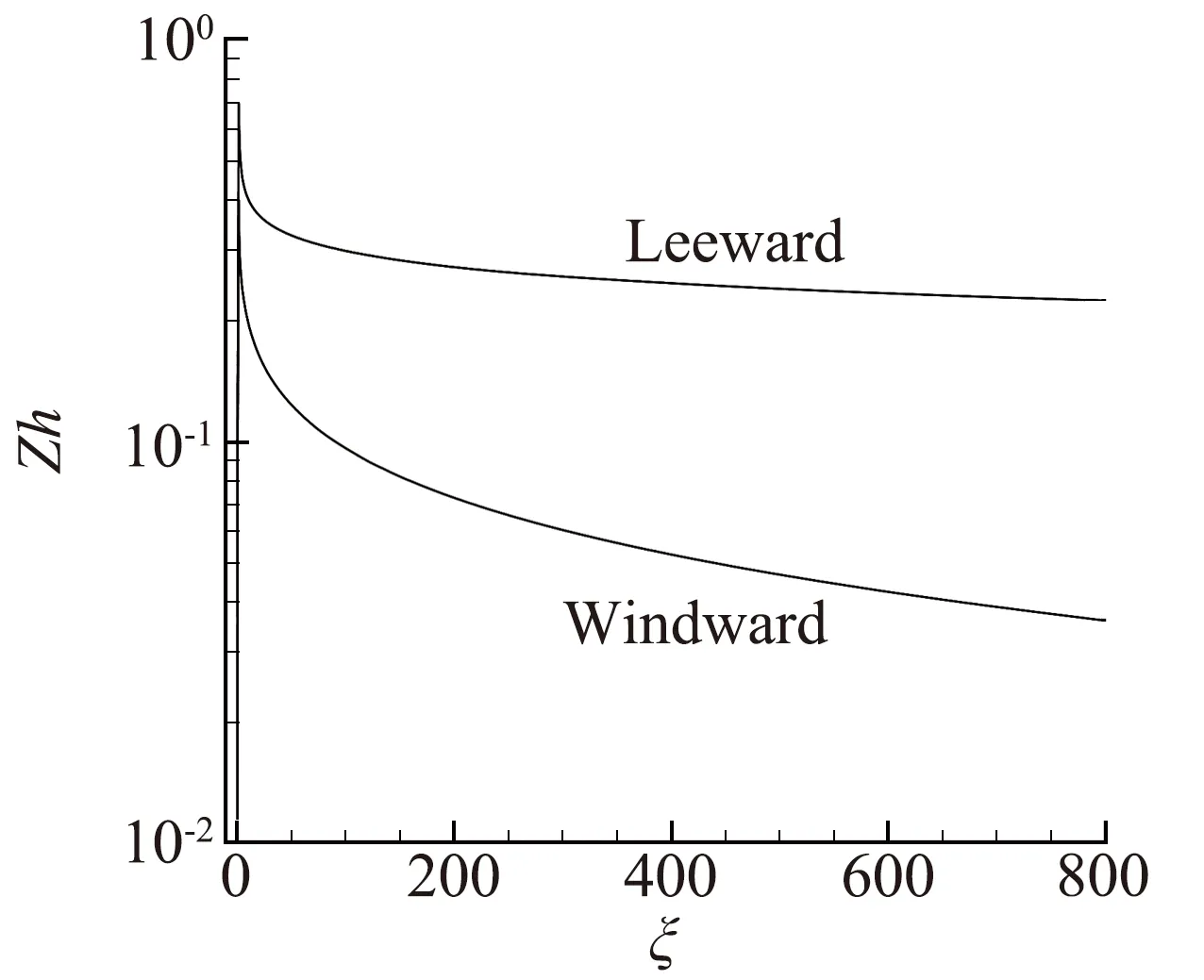
(a) NS:背风面与迎风面壁面Zh值沿壁面的分布
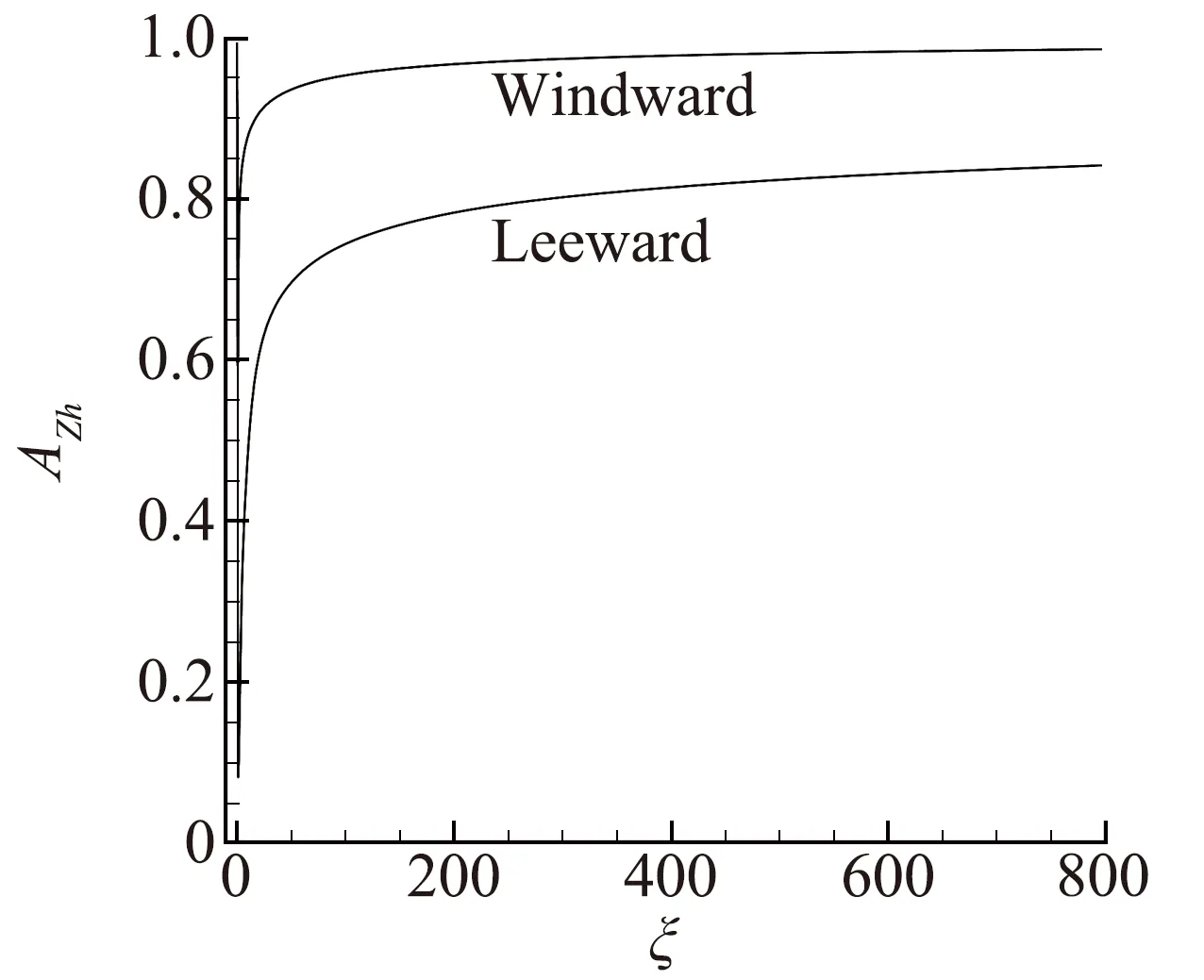
(b) NS-VC:壁面修正系数沿壁面的分布
图6给出了有黏性修正与无修正情况下壁面压力、壁面摩擦系数以及相对变化率(σDev)沿壁面的变化,其中相对变化率是(NS-VC结果-NS结果)/(NS结果)。从图中可以看到黏性修正使得壁面压力与壁面摩擦系数均减小,其中对背风面的影响比迎风面大很多。由图6(a)可以看到,黏性修正使得背风面的壁面压力相对于无修正来说在大部分地区均约减小6%左右。而图6(b)可看出,黏性修正使得背风面的壁面摩擦系数相对于无修正来说减小最多为57%,而在ξ>100以后,则从11%逐步降至7%左右。即稀薄效应对背风面的壁面压力以及摩擦力均会造成比较大的影响。但对迎风面来说,则稀薄效应的影响很小。
图7给出了背风面与迎风面在x*=1 m处速度沿壁面法向分布的剖面。由图7可以看到,黏性修正使得边界层内的速度梯度增大,在背风面的修正效果比迎风面强很多。
2.2 迎角的影响
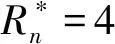
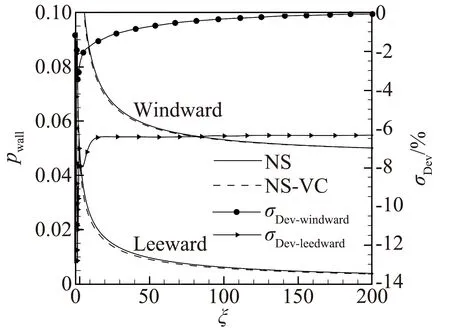
(a) 壁面压力
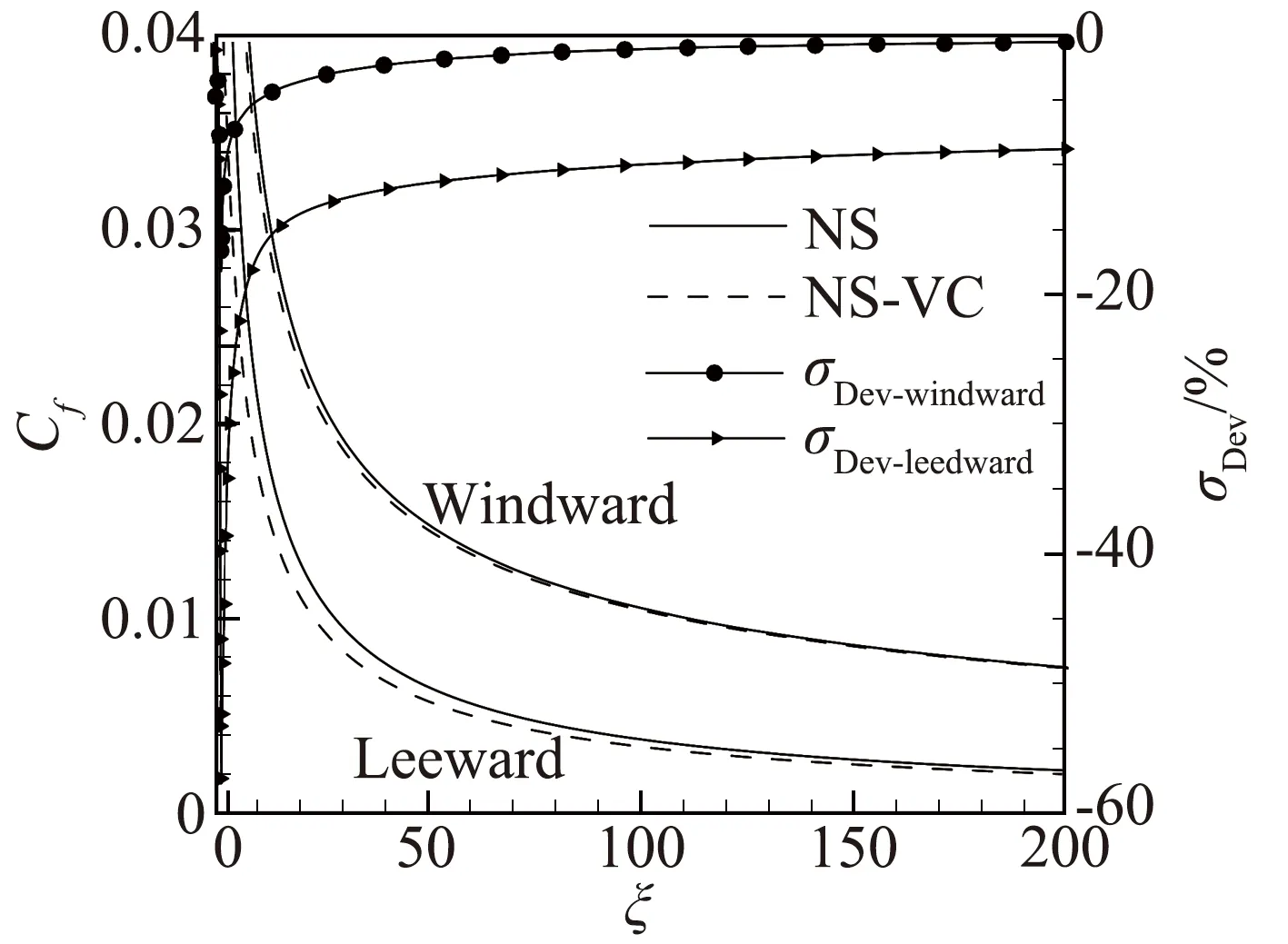
(b) 壁面摩擦系数
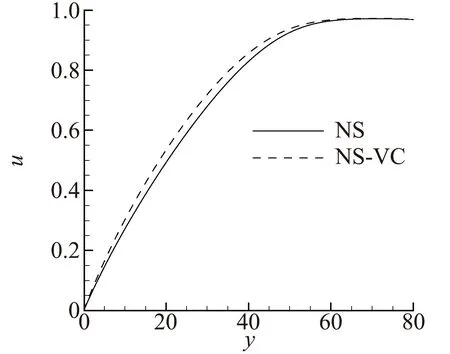
(a) 背风面
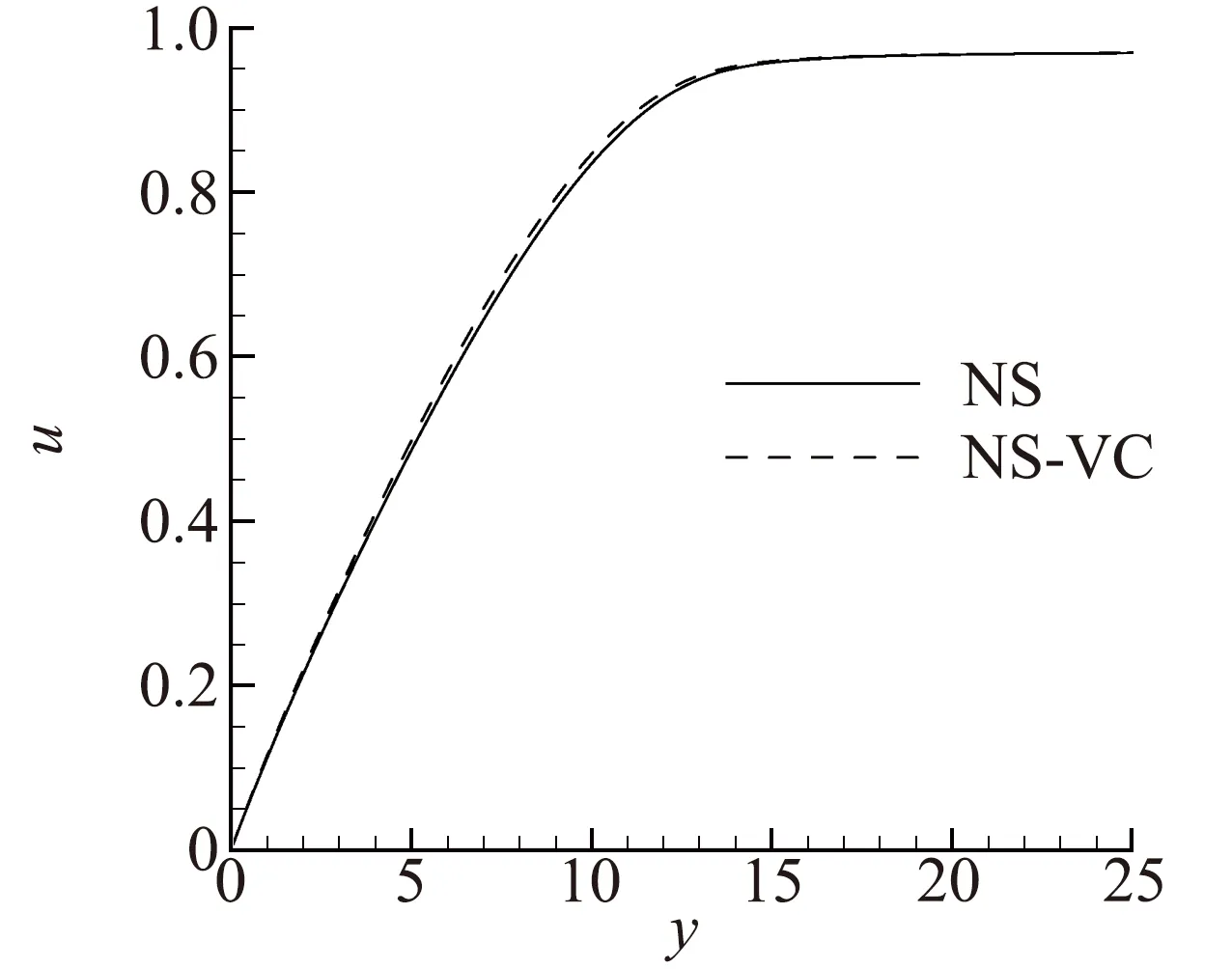
(b) 迎风面
图8给出的是迎角分别为5°、7.5°、10°情况下背风面壁面Zh值随壁面弧长的变化,右上角为头部的局部放大图,圆头与平板相切的位置大约在ξ=1.57 处。可以看到不同迎角的壁面Zh值变化规律相似,都是先增大后减小,在头部附近急剧变化,并在圆头与板身相切的位置附近取得最大值。对比三个迎角的结果可以发现,迎角越大,其背风面壁面Zh值越大,表示其稀薄程度也越大。
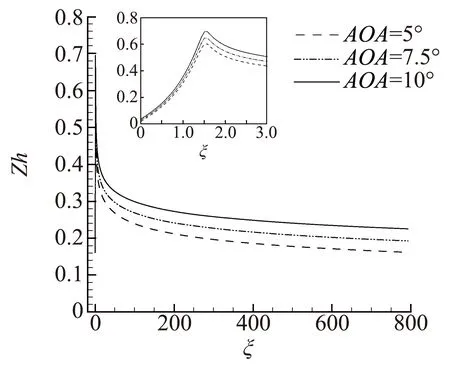
图8 不同迎角背风面壁面Zh值沿壁面的变化Fig.8 Variation of Zh value along the wall surface of the leeward with different angles of attack
表2给出的是不同迎角下有黏性修正和无修正情况下头部的压力和摩擦力产生的升力和阻力,表3给出的是整体的升力、阻力以及升阻比,表4给出的是板身部分上下板的压力以及摩擦力分别对升力、阻力的贡献,同时表2、表3、表4中都给出了黏性修正后的结果相对于无修正的变化率(σDev)。
由表2与表3对比可以看到,头部的升力相对于总的升力来说很小,几乎可以忽略,头部的阻力和总的阻力相比不能忽略,黏性修正使得头部阻力的减小大约在3%左右。由表4可以看到,当迎角由5°变到10°,黏性修正使得上、下板压力与摩擦力均减小,其中上板摩擦力减小8.42%~13.13%,上板压力减小4.31%~6.43%,下板摩擦力减小2.92%~1.60%,下板压力减小0.85%~0.18%。因此,黏性修正主要对上板产生影响,而对下板影响比较小,并且迎角越大,上板的稀薄效应越强,黏性修正使得上板压力、摩擦力减小越多。同时可以看到,升力主要由上、下板的压力贡献,而阻力由上、下板的摩擦力以及下板压力贡献。综合头部与板身的效果,由表3可以看到,黏性修正使得最终的升力增加0.5%左右,阻力减小3.4%~1.71%,升阻比增加4.13%~2.23%。因此,稀薄效应存在时, NS方法预测的升力会比实际的偏小,而阻力比实际的偏大,导致其预测得到的升阻比偏小。迎角越大,上板的稀薄效应越大,但从表3看到黏性修正后升阻比的增加反而越小。这是由于随着迎角变大,下板压力迅速增大,使得下板压力对升力以及阻力的贡献都迅速增大(见表4),由此使得上板对升力阻力贡献在总的升力阻力里面占的比重都越来越小,而黏性修正对下板影响很小,最终使得迎角越大升阻比变化越小。
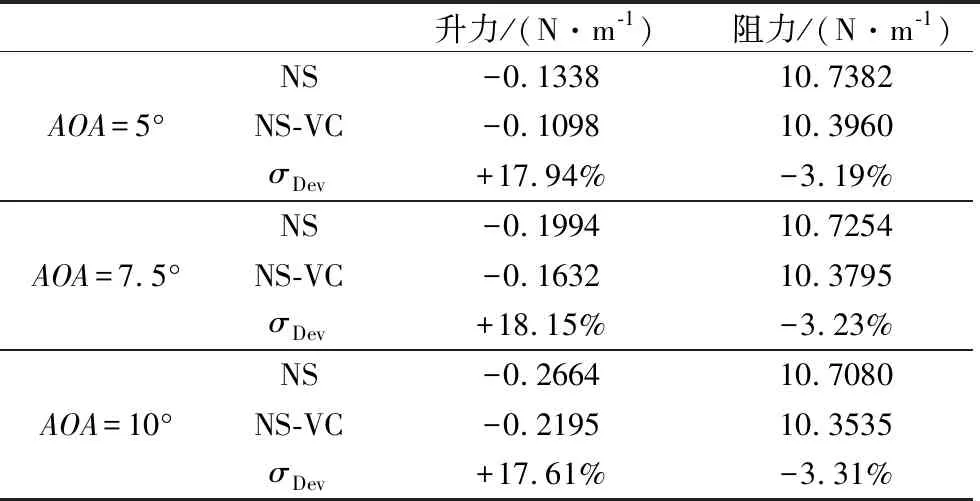
表2 不同迎角下升力、阻力表(积分从x*=-4 mm到x*=0 mm,仅头部)Table 2 Lift and drag with different angles of attack(Integral from x*=-4 mm to x*=0 mm, only the head)
2.3 球头半径的影响
图9给出了在迎角为5°时头部半径分别为4 mm、20 mm、200 mm ( Case 1、Case 4、Case 5 ) 壁面Zh值随壁面弧长的变化。可以看到,头部半径越大,Zh值越小,表明稀薄效应越小,其越趋于连续流。
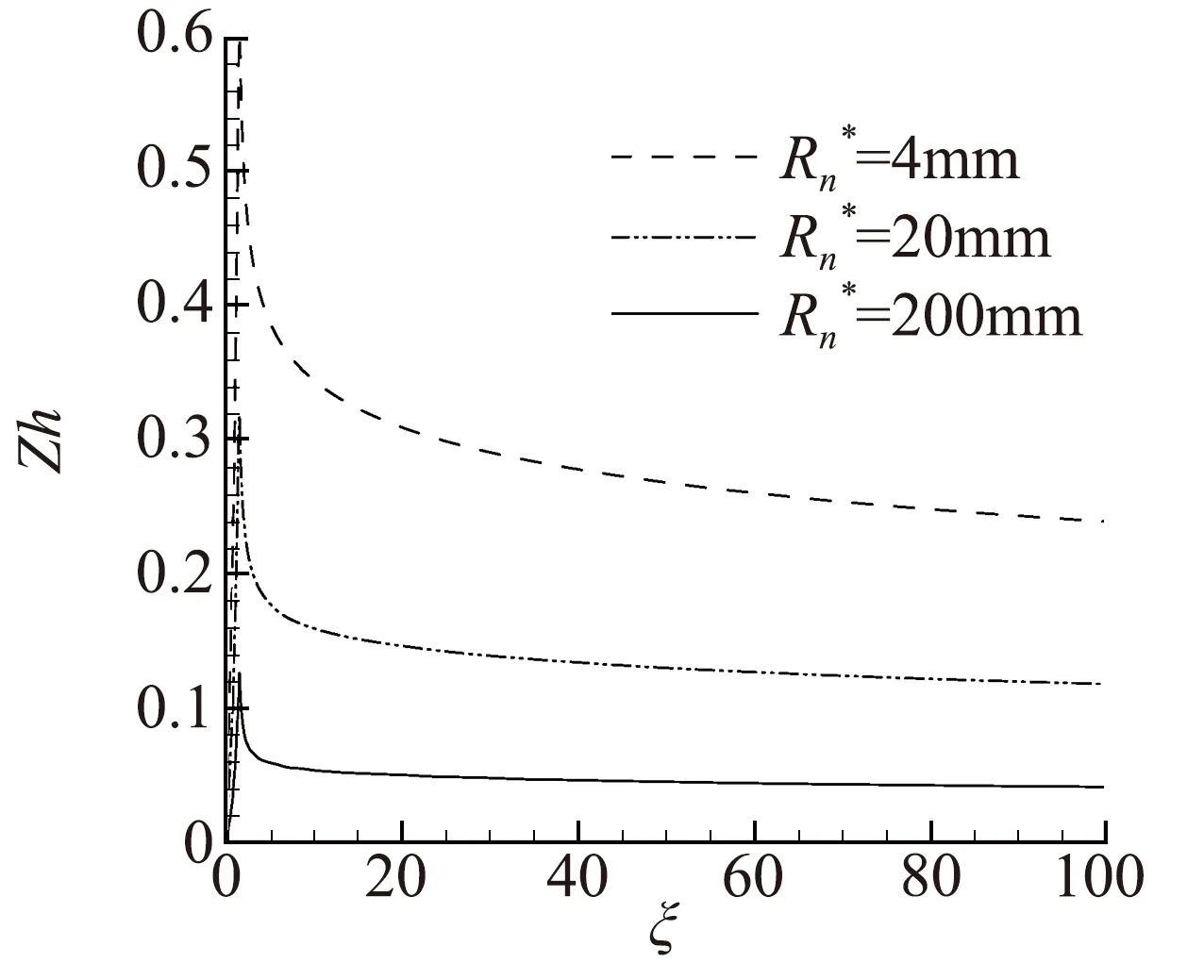
图9 不同头部半径壁面Zh值沿壁面的变化Fig.9 Variation of Zh value along wall surface with different head radii
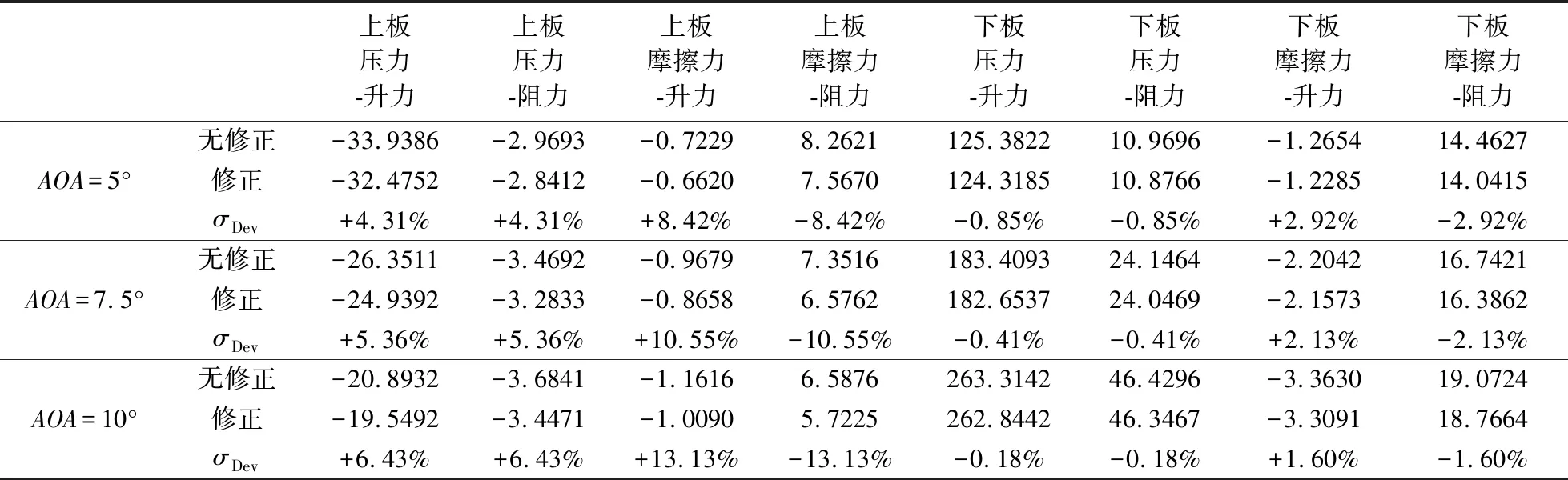
表4 不同迎角上下板的压力、摩擦力对升力、阻力贡献表(单位:N/m)(积分从x*=0 mm到x*=3000 mm,仅平板部分)Table 4 The contribution of pressure and friction of upper and lower plate to lift and drag(Integral from x*=0 mm to x*=3000 mm, only the plate)
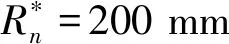
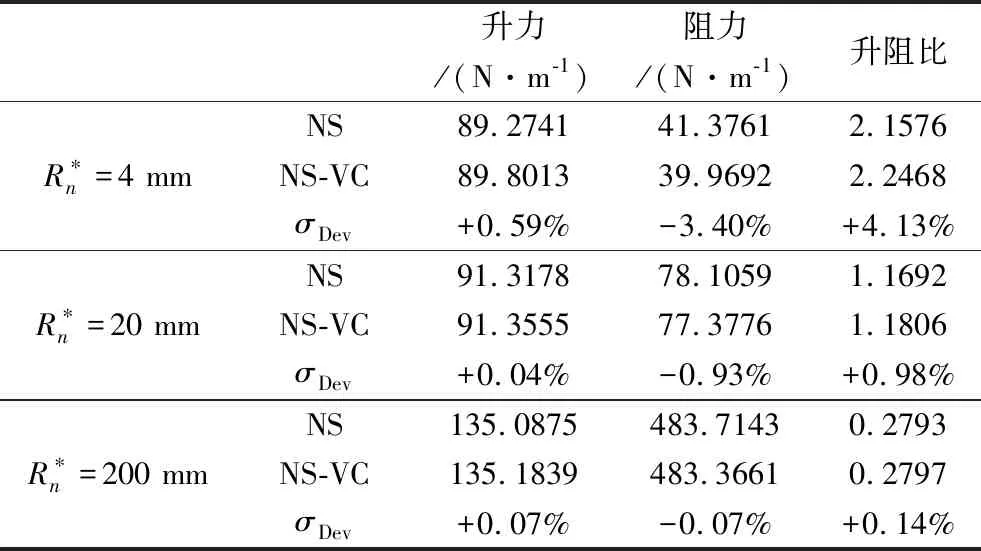
表5 不同圆头半径升力、阻力、升阻比表(积分从前缘到x*=3000 mm)Table 5 Lift, drag and lift-drag ratio with different head radii (Integral from leading edge to x*=3000 mm)
3 结论与讨论
本文的主要目的是看文献[1]中提出的通过等效黏性考虑局部稀薄效应的结果是否能方便地应用于空气动力学计算中,也要看应用后得到的结果是否更符合实际。这两点都已得到正面的结果。第一,的确可以方便地应用于空气动力学技术中,而且所增加的时间非常有限,计算量的增加在50%以下。第二,所得结果和传统的计算方法所得结果相比,壁面摩擦系数减小,升阻比增加,其改进的方向与现有飞行试验结果定性相符。本文还进一步分析了迎角及球头半径的影响。
但是需要说明的是目前所做只是初步的尝试,真正解决实际问题,还有以下问题需要进一步考虑:
1) 本文所用的黏性系数的修正系数与参数Zh的关系是针对单元子气体氩气获得的,对真实的空气来说,即使定性上相似,定量上也会有一定程度的不同。
2) 由于在文献[1]中的DMSC计算中,黏性与温度的依赖关系采用了硬球模型的根号关系,与传统CFD中用的公式有一定的差别。在用于实际问题时,需要重新考虑。
3) 本文没有考虑稀薄效应对CFD中壁面条件的影响。
4) 高超声速流往往伴随有高温及热传导问题。这里稀薄效应对热传导的影响考虑的还不全面。因此,稀薄效应对热传导问题的影响,热传导对黏性的影响以及传热和黏性在稀薄效应下的相互影响也是今后需要考虑的问题。
致谢:感谢周恒院士给予的直接指导帮助。
