基于Hilbert-Huang变换的轴频电场信号检测方法∗

吴 亮 赵 哲 苏建业 崔 培

（1.海军驻大连地区军事代表室 大连 116021）（2.大连测控技术研究所 大连 116021）

1 引言

船舶轴频电场信号主要由船体的腐蚀电流和防腐系统外加的保护电流经螺旋桨主轴调制产生，其产生机理如图1所示。腐蚀电流和保护电流以海水为介质从船壳流向螺旋桨，然后经过船体内部各种轴承、密封和机械等线路返回船壳，构成一个封闭的导电回路。由于该回路中的电阻RB会随螺旋桨主轴的旋转而周期性变化，会对流经海水的电流进行调制，从而形成以螺旋桨转速为基频的极低频电场信号［1］。大量理论分析与实测数据均表明该电场信号具有明显的线谱特征的，其基频与螺旋桨转速密切相关，频率范围大约为1Hz～7Hz，可以作为探测水中目标的理想信号源［2］。

船舶产生的轴频电场信号在海水中随传播距离的增大而快速衰减，因此在距离目标较远时，轴频电场信号容易被海洋环境电场噪声所掩盖，增加了探测难度。为提高对船舶轴频信号的检测能力，国内学者进行了详细而深入的方法。卢新城、龚沈光等应用快速横向滤波器自适应算法，通过自适应谱线增强器，能实时有效地将微弱的窄带轴频电场信号从宽。马育锋、龚沈光等提出了一种基于小波变换的目标轴频电场信号检测方法［3］；李松提出了一种基于功率谱估计的船舶轴频电场信号提取与检测方法［4］；李松、卢新成等应用高阶累积量对高斯色噪声的抑制作用提出了基于维谱的舰船轴频电场线谱提取方法［5］。

Hilbert-Huang变换是一种适用于非线性、非平稳信号的处理方法，具有良好的客观性和自适应性，该方法已在故障诊断、地震信号分析、流体力学等领域取得了很好的应用［6～9］。 本文将 Hilbert-Huang变换应用于轴频电场信号的提取，通过对已知信号进行仿真模拟，讨论该方法的有效性；然后对轴频电场信号进行尺度经验模态分解和希尔伯特变换，通过对固有模态函数进行有效的阈值滤波，然后进行信号的重构，获得有效轴频电场信号。

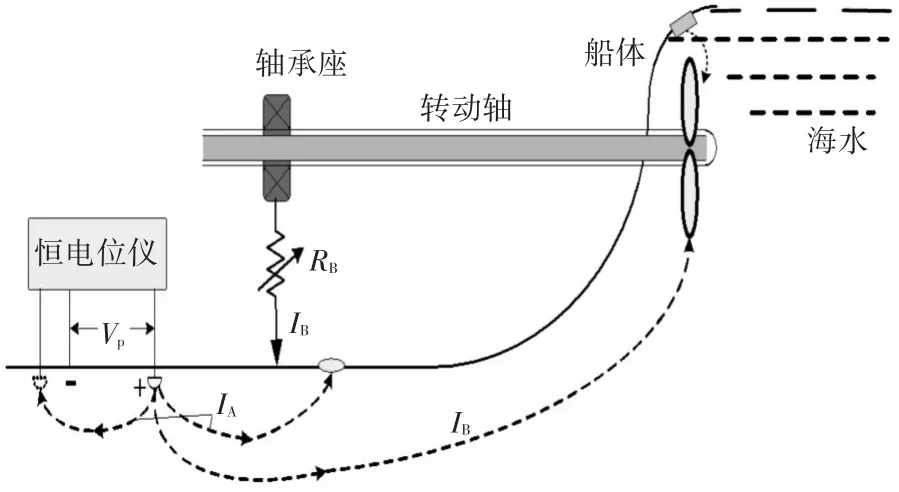
图1 船舶轴频电场信号产生机理

2 Hilbert-Huang变换基本原理

Hilbert—Huang变换由两个步骤组成。第一步，通过经验模态分解方法（EMD-Empirical mode composition method）获得信号的有限数目的固有模态函数（IMF-Intrinsic mode function）；第二步，对每个IMF利用Hilbert变换获得信号的时-频谱即Hilbert谱［10］。

2.1 经验模态分解

经验模态分解（EMD）是指通过信号分解，将复杂的信号分解为有限个单分量信号之和。为了保证每个固有模态（IMF）是单分量的，需满足以下两个条件：

1）在整个信号长度上，一个IMF的极值点和过零点数目必须相等或最多只相差一点。

2）在任意时刻，由极大值点定义的上包络线和由极小值点定义的下包络线的平均值为零，即IMF的上下包络线对称于时间轴。

假设获取的轴频电场信号为x(t)，则EMD分解的步骤如下：

1）找到轴频电场信号所对应的极大值与极小值，通过对这些极大值与极小值的三次样条拟合，可以分别得到信号的上包络曲线与下包络曲线，计算上包络曲线与下包络曲线在每一个点上的平均值，得到一条平均值曲线m10。用信号每一点的值x(t)减去该点的m10，可以得到新数据h10：

此时得到的h10一般不满足IMF所需的两个条件，因此对得到的新数据重复n次以上过程，使最终所得的平均包络曲线趋近于0，则h1n就是信号的第一阶IMF分量，用c1表示，用x(t)减去c1可以得到第一阶剩余项r1：

2）对第一阶剩余项r1重复以上过程，可以第二阶IMF分量c2。通过多次对信号的经验模态分解，可以得到多个IMF分量以及一个逼近分量rn。因此信号可以表示为如下形式：

从EMD分解的过程可以发现，越早分解出的IMF分量所对应的频率越高。经EMD分解得到的IMF分量是多通带滤波的结果，并且每个IMF分量均是稳态的，可用于Hilbert变换或其他适用于稳态信号的处理方法。

2.2 Hilbert变换

对经EMD分解得到的每阶IMF分量（c(t)）进行Hilbert变换，可以得到对应分量的瞬时频率：

其中 p是Cauchy主值。c(t)与 y(t)组合成解析信号z(t)，用极坐标的形式可以表示为

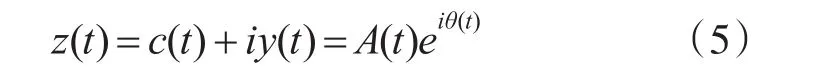
解析信号的极坐标形式反映了Hilbert变换的物理含义：它是通过一正弦曲线的频率和幅值调制获得信号局部最佳逼近。根据瞬时频率的定义：

对每一阶IMF分量ci作Hilbert变换，并根据上式可以得到相应解析函数的幅值谱和瞬时频率，因此原始信号x(t)可以表示为

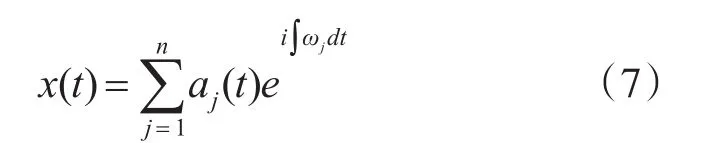
式（7）反映了信号的幅值、时间和瞬时频率之间的关系。取式（7）的实部并定义为Hilbert谱，用H(ω，t)表示。对其进行时间积分可以得到信号x(t)的Hilbert边际谱：

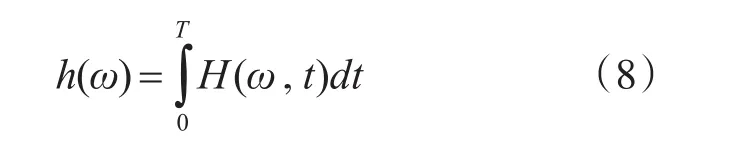
Hilbert边际谱可以表示每个频率在全局上的幅度（或能量），是信号每个频率点的积累幅值在统计意义上的表示。

3 仿真信号的Hilbert-Huang变换

为了验证Hilbert-Huang变换对轴频电场信号的处理效果，设计了基频为2Hz、调频为0.01Hz，并且包含0.05Hz极低频干扰与50Hz工频干扰的信号，其解析表达式为

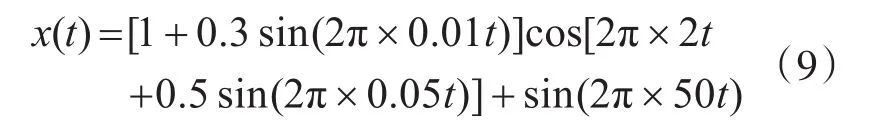
对仿真信号进行EMD分解可以得到如图2（a）所示的6条曲线，图2（b）中为所对应的信号及IMF分量的频谱。其中，Initial signal为式（9）所示的仿真信号；imf1代表第一阶IMF分量（c1），为最先被分离出来的高频信号，对应50Hz的干扰；imf2代表第二阶IMF分量（c2），是第二次被分离出来的2Hz

轴频信号；imf3、imf4和r分别代表第三阶（c3）、第四阶（c4）和剩余量（r5）。其分解结果与图3（b）中所示频谱一致。

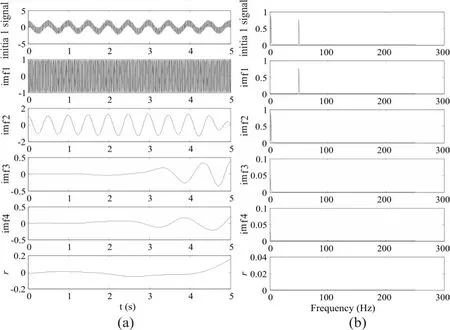
图2 仿真信号EMD分解结果及对应频谱

对EMD分解得到的5阶IMF进行Hilbert变换，并综合各阶瞬时频率谱可以得到仿真信号的HHT时频谱，如图3所示。从时频谱图中可以看出各个已知频率成分的能量分布随时间和频率的动态变化特征，呈带状或波浪状分布，根据各分量的谱值能区分出能量随时间和频率的细微变化。带状与波浪状图形分布表示信号的能量相对集中，集中程度和形成的谱值空间图像正好反映了调频调幅成分与正弦信号成分的实际变化特征［11～12］。

4 轴频电场实测信号分析

4.1 轴频电场实验室测量

轴频电场的实测工作利用船模在水池内完成，无磁性实验水池的尺寸为长8m、宽5m深3m，在水池中加入1.5m深的、电导率为0.3S/m（20℃）的海水来模拟的海洋环境。水池测试时使用长度为1.5m的潜艇模型，其螺旋桨材料为黄铜的3片桨叶，如图4所示。为了增大流经艇模轴系的电流强度，外加一定的电流，同时螺旋桨在电机的带动下以1.17Hz的频率转动。轴频电场的测试系统主要由电场传感器、信号调理模块以及数据采集模块组成。

图3 仿真信号的HHT时频谱

图4 艇模

在距离艇模螺旋桨6m处获得一组信噪比较低的实测轴频电场信号，如图5所示。

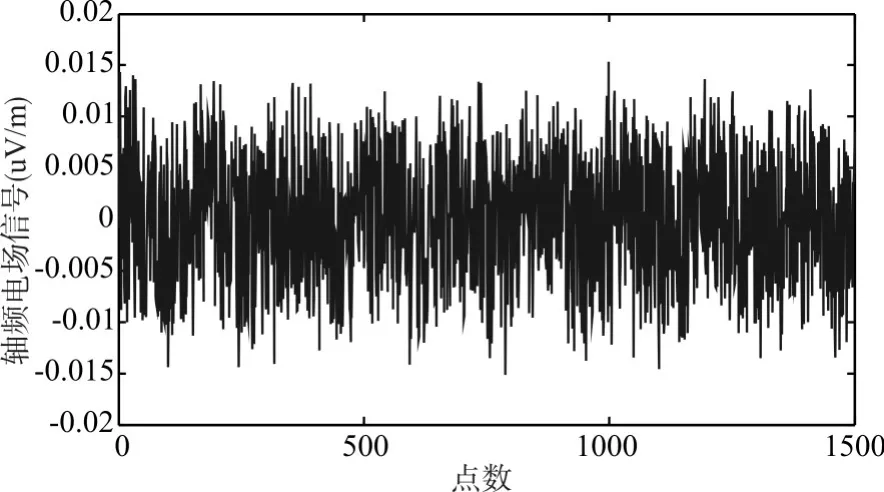
图5 轴频电场信号

4.2 实测轴频电场信号的Hilbert-Huang变换

对实测信号进行EMD分解，可以得到如图6所示的11条曲线，其中signal为轴频电场实测曲线。imf1-imf9、r分别为经EMD分解得到的9个固有模态曲线及剩余量。结合固有模态曲线和相应的频谱图可以发现，第1阶IMF分量主要为50Hz工频干扰，第2阶到第5阶分量为低频干扰噪声；第6阶分量与第7阶分量主要为轴频电场信号；第8阶分量、第9阶分量主要为1Hz以下干扰。剩余量r代表了振动和电极之间的线阻所带来的干扰。

图6 轴频电场信号EMD分解结果

图7 轴频电场信号的HHT时频谱

通过对EMD分解结果做Hilbert变换，并综合各阶瞬时频率谱可以得到实测轴频电场信号的HHT时频谱，如图7所示。图中不同颜色的点表示能量，颜色越亮，代表着能量越高，反之，能量越低。从图7可以看出，实测轴频电场信号能量主要集中在10Hz以下的低频部分，并且存在1.17Hz的持续信号。

5 结语

本文提出了一种基于Hilbert-Huang变换的轴频电场信号检测方法，进行了仿真实验和实验室实测数据处理分析，分析结果表明Hilbert-Huang变换得到的各阶IMF分量及其瞬时频率可以客观描述轴频电场信号的特性，并能有效识别轴频信号的干扰，得到的HHT时频谱能够反映轴频电场信号随时间和频率动态变化在不同阶段的主要特征，可以应用Hilbert-Huang变换来进行轴频电场信号的检测以及噪声抑制。