基于递归细化和局部方差的目标靶边缘检测∗

李浩谊 马春庭

（中国人民解放军陆军工程大学石家庄校区火炮工程系 石家庄 050003）

1 引言

在相机的标定过程中，需要对目标靶图像进行信息的快速提取，边缘检测是相机标定过程中的一项重要步骤［1］。最常用的相机标定方法是张正友标定法，使用的目标靶是单平面棋盘格。但由于噪声的存在会使图像产生光斑、边缘不连续等不良影响，容易产生伪边缘并且增加检测时间，因此，提高边缘检测的准确性和实时性具有十分重要的意义［2］。

目前采用的一阶边缘检测算子有Sobel算子、Prewitt算子、Robert算子等，实时性较好，但检测的边缘比较粗糙，反映色边界信息较小；二阶边缘检测算子有Canny算子、LOG算子和Laplician算子等，反映的边界信息包括了许多的细节信息，但准确性不理想，容易受到噪声的干扰［3］。张宇伟等［4］提出了一种结合Sobel算子和小波变换的图像边缘检测方法，但是该方法运算量大，实时性较低。李俊山等［5］提出了一种改进的Canny图像边缘检测方法，但是该方法对冲击噪声比较敏感，容易检测出伪边缘，导致边缘的信噪比变小，当噪声密度较大时，容易出现噪声像素统计为弱边缘现象。

图像的边缘是灰度值波动较大的区域，局部方差表示数据的波动程度，因此能够作为边缘检测的依据［6］。本文提出一种基于递归细化和局部方差的目标靶边缘快速检测。结果显示：相比其他常用算法，本文算法能在边缘检测准确性和实时性上均获得良好性能。

2 基于局部方差的快速边缘检测算法

2.1 传统的基于局部方差的边缘检测算法

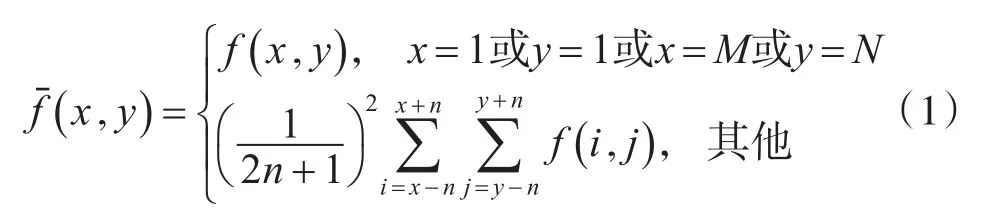
对 σ2(x ，y)进行量化处理，量化步阶为2-L，并将处理后的σ2(x ，y)称为图像的局部方差图。在局部方差图中，灰度值大的像素点对应着原图中的边缘和噪声。

根据式（3），通过阈值的设定［7］，在局部方差图中得到二值化图像。

阈值T的计算公式如式（4）所示：

2.2 基于积分图像和Otsu方法的局部方差的边缘快速检测算法

图像的局部方法计算复杂，耗时长，实用性低，因此，本文利用积分图像降低计算局部方差的时间复杂度，并采用Otsu方法计算阈值，显著地降低时间复杂度。

2.2.1 结合积分图像的局部方差快速算法

结合式（1）、（2），得到式（5）

图像中共M×N个像素点，每个局部区域共有k2个像素点，传统方法的时间复杂度为而利用积分图像计算局部方差的时间复杂度为O(M ×N )，时间复杂度明显减小。

2.2.2 Otsu方法

假定 pr(rq)为局部方差图中灰度值为rq的像素出现的概率，即：

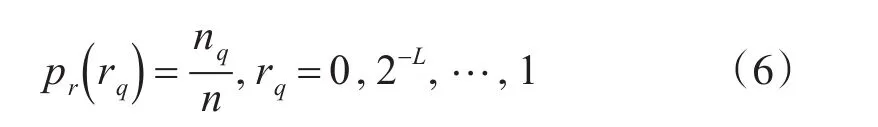
n为图像的像素总数，nq为灰度值为rq的像素数目，L为图像中所有可能的灰度级数。

阈值k使得图像分成两类，即C0是一组灰度级为{0 ，1，2，k-1} 的像素，C1是一组灰度级为的像素。设表示阈值为k时的类间方差，则最佳阈值可以通过求的最大值而得到，即：

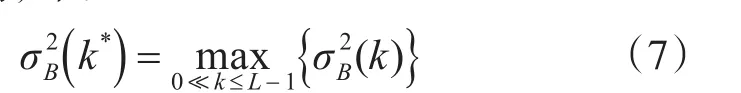
根据式（8），通过阈值的设定，在局部方差图中得到二值化图像。

如图1所示分别利用传统的基于局部方差的边缘检测算法和基于积分图像和Otsu方法的局部方差的边缘快速检测算法进行边缘检测，可以看出两种算法处理效果基本一致，检测出的边缘效果理想。表1给出了不同边缘检测算法处理不同总像素数图像所需时间，由结果可以看出，随着总像素数的增加，本文算法比传统的基于局部方差的边缘检测算法更快，所需时间在一阶检测算子与二阶检测算子之间，满足实际工作要求。

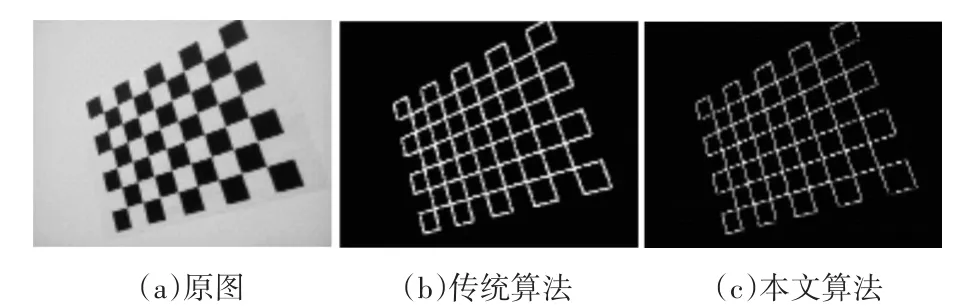
图1 传统的基于局部方差的边缘检测算法与本文算法处理效果

表1 不同边缘检测算法处理不同总像素数图像所需时间（s）

3 递归细化算法

3.1 建立强边缘宽度-频数图

通过上文算法的边缘检测，可以得到强边缘的位置，即图1（c）中白色像素点的位置，从而可以在局部方差图中进行强边缘宽度的计算［8］。

结合文献［9］的方法和本文以图像局部方差作为边缘位置定位的依据，定义强边缘宽度的计算。

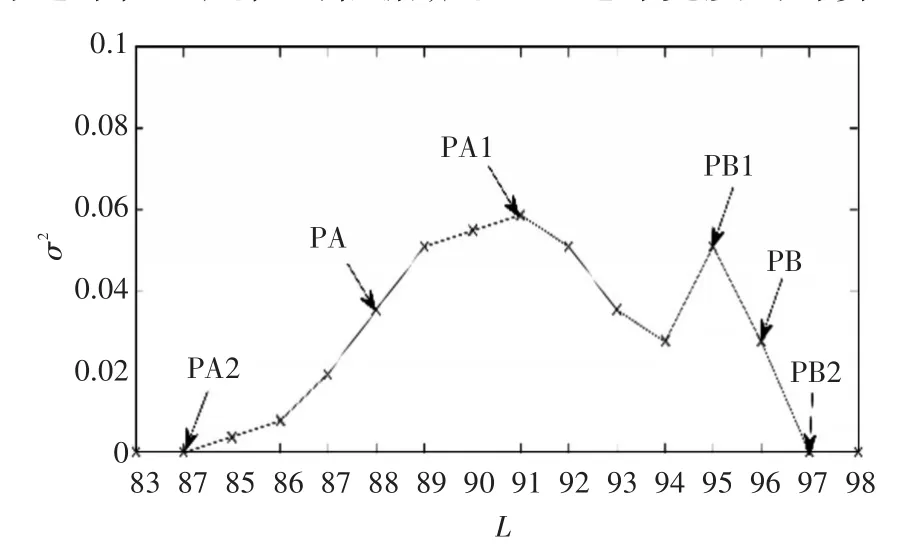
图2 局部方差图的一行

对于竖直方向强边缘上的某一点，在局部方差图中找到该点水平方向上最接近该点的左右局部方差极值点。这两极值点可以认为是边缘的起始点和结束点，因而两极值点位置差即为该点所求得的强边缘宽度。如图2所示，PA与PB为检测到的强边缘上的像素点，PA1为极大值点的横坐标，PA2为极小值点的横坐标，则PA所对应的强边缘宽度为PA1-PA2；PB1为极大值点的横坐标，PB2为极小值点的横坐标，则PB所对应的强边缘宽度为PB2-PB1。对所有竖直方向上的强边缘点进行相同计算可以得到该方向上强边缘的所有宽度。

对于水平方向强边缘的宽度计算也是类似，它求取的是边缘点竖直方向上最接近该点的上下局部方差极值点，从而得到水平方向强边缘的宽度。

由于在棋盘格靶板中，直线为主要的几何元素，可以认为直线的宽度出现的概率是最大的，即在图3强边缘宽度-频数图中，峰值部分所对应的强边缘宽度即为直线宽度。

图3 强边缘宽度-频数图

3.2 设定直线最小宽度

二值化图像由一系列离散的像素组成，像素值是0或1，显示的直线会出现锯齿形成或台阶状的边缘，如图4所示。这种用离散量表示连接量所造成的失真效果，称为走样［10］。

图4 二值化图像中直线走样

结合文献［11］，本文设定直线最小宽度为2个像素点，并提出如下的判断直线宽度是否满足条件的判据：若直线在垂直方向和水平方向的强边缘宽度都不大于直线最小宽度，则认为边缘检测符合要求；否则对原始图像中强边缘位置点进行下文的遍历八方向的直线细化处理。

3.3 遍历八方向法的直线细化

根据图像的相关性，一个没有受到噪声污染的像素点一定会与其周围某个邻域内的统计特性相关，表现在图像上就是其灰度级一定会与其周围某个邻域的灰度级接近，除非该奇异点出乎意料的表示了有用信息而非噪声的小概率事件的发生［12］。若强边缘宽度不满足上文的判据，表示边缘存在噪声或其他因素导致该处局部方差值过大，因此对强边缘点进行下列处理。

图5 点f(i ，j) 的5×5邻域矩阵

当遍历八方向法的直线细化处理完成时，再使用基于积分图像和Otsu方法的局部方差的边缘快速检测算法对原图像进行处理，判断直线宽度是否满足条件，递归循环直至直线的宽度符合条件。算法流程图如图6所示。

4 实验结果与分析

为了验证本文算法的性能，设计了3个实验：实验1为本文算法的处理效果；实验2为验证本文算法的抗噪能力；实验3为本文算法的边缘细化效果。

仿真实验在MatlabR2016a环境下，Intel®Core™i5-6500 CPU 3.20GHz/8.00GB内存的机器上进行。

4.1 实验1本文算法的处理效果

为了验证本文算法的处理效果，选取不同角度下的目标靶图像，分别采用Sobel算法、Canny算法和本文算法对图像进行边缘检测并进行主观分析和客观评价，边缘检测结果如图7所示。其中，图7从上往下分别为目标靶图像的正视图、斜视图和旋转图。

图6 本文算法流程

图7 本文算法与常用边缘检测算法对比

1）主观分析

观察图7，Sobel算法检测出的结果边缘连续，直线宽度满足条件，但容易受噪声的影响，在噪声影响区域效果不理想；Canny算法检测到的边缘存在虚假边缘，直线交点处过渡不自然；本文算法检测到的边缘连续较细，准确性较高，抗噪能力较强。

2）客观评价

为了更客观地对图像边缘检测的结果进行评价，本文采用了文献［13］提出来的边缘检测性能品质因数进行评价，评价公式为

其中m是理想状态下边缘点数目，n是检测出的边缘点数目，α为比例系数，当检测出的边缘点是主边缘线上的点时，α=1，d(i)表示实际边缘与检测到的边缘的距离，F的值在0到1之间，当F=1时是检测的理想状态，其值越大，说明边缘检测效果越好，准确性越好。本文算法与对比算法得到的品质因数见表2。

表2 各边缘检测算法FOM值

实验结果表明，本文算法的FOM值均比其他算法接近1，则本文算法边缘检测效果较好。

4.2 实验2本文算法的抗噪能力

为了验证本文算法的抗干扰能力，本文实验采取具有不同噪声水平的目标靶像进行边缘检测并进行对比。噪声通过手动叠加不同噪声水平的高斯白噪声组成，噪声水平由噪声的标准差控制，不同噪声水平的图像边缘检测结果如图8所示。

从图8可以看出，随着高斯白噪声水平的逐渐增加，图像的污染程度越严重。但是本文算法的边缘检测仍能得到很好的效果，这说明本文算法的抗噪能力很好。

图8 不同高斯噪声水平下的边缘检测结果（左边为带有噪声的原图像，右边为边缘检测结果）

4.3 实验3本文算法的边缘细化能力

为了验证本文算法的边缘细化能力，本文实验采取模糊的目标靶图像进行边缘检测，记录递归细化算法的次数并对实验结果在相同位置进行放大和对比，边缘检测结果如图9所示。其中，图9（a）为模糊图像，图9（b）为没有进行直线细化处理（n=0）的局部放大图像，图9（c）为进行了一次直线细化处理（n=1）的局部放大图像，图9（d）为进行了两次直线细化处理（n=2）的局部放大图像。

图9 直线细化不同次数的效果对比

观察比较图9（b）、（c）、（d），对于模糊图像，检测的直线宽度必然增加，随着细化次数的增加，直线的宽度减少，效果显著。这说明本文的直线细化处理效果明显，能有效减少检测直线的宽度，提高准确度。

5 结语

本文通过积分图像的特性加快局部方差的计算时间，结合图像的相关性利用递归循环的方法细化边缘直线，完成目标靶的边缘检测。实验结果表明，该算法比传统的基于局部方差的边缘检测算法耗时小，计算量大大减少；比常用的一阶和二阶边缘检测算法效果好，检测到的边缘连续清晰、边缘宽度合适。因此本文算法具有较好的准确性和实时性，为以后在亚像素精度上定位直线的研究提供了新的途径。