基于精英反向学习的混沌蝙蝠算法∗

郭 旭 贺兴时 高 昂

（西安工程大学理学院 西安 710048）

1 引言

蝙蝠算法（Bat Algorithm，BA）作为一种模拟蝙蝠回声定位行为的新型元启发式优化算法被广泛应用于多目标优化，以及诸多经典的全局工程优化问题［1～3］。BA结构简单、参数少、鲁棒性强，但本身也存在着容易陷入局部最优、算法执行后期的寻优精度不足等问题。文献［4～7］分别提出了将BA同和声搜索算法、模拟退火算法、遗传算法以及差分进化算法相结合的混合启发式算法，不同程度上提高了算法的收敛速度与搜索精度。此外，刘长平等针对基本蝙蝠算法收敛精度低和易早熟，采用levy飞行搜索策略来模拟蝙蝠的捕食行为，使得该算法有效地避免了局部极值的吸引［8］。张宇楠、盛孟龙等人分别将自适应步长、自适应变异策略引入蝙蝠算法，从而使算法在后期获得更高精度的解［9～10］。孙文捷、刘长平等分别将基于Fuch映射和逻辑自映射的混沌算法引入到蝙蝠算法中，有效地结合了蝙蝠算法的全局优化能力和混沌算法的局部搜索能力［11～12］。而关于蝙蝠算法的理论性分析，李枝勇等将蝙蝠算法简化到一维的单个蝙蝠，定义了速度和位置更新的两种模式，利用特征方程的方法分别对其进行了收敛性分析［13］。盛孟龙等基于随机搜索算法的全局收敛性判断准则对蝙蝠算法的收敛性进行分析［14］。

为了更好地控制蝙蝠算法的探测和开发能力，克服基本蝙蝠算法缺点，引入精英反向学习机制，通过对比精英蝙蝠的当前解与反向解，选取较优秀个体进入下一次迭代，加快算法收敛速度。同时，在迭代中对蝙蝠位置进行混沌扰动，增加种群多样性，这在一定程度上能有效地提高了算法的全局搜索能力和搜索精度。

2 基本蝙蝠算法

蝙蝠借助其特有的“声呐系统”在黑暗的环境中躲避细如发丝的障碍物并捕食猎物［15～17］。蝙蝠算法即是模拟蝙蝠生物学行为并进行优化的一种基于群体进化的算法。

首先在可行解空间随机初始化种群，即确定个体的初始位置和初始速度，其中位置用来表示问题的解，通过评价群体，找出群体最优位置，然后分别按式（1）～（3）更新个体的飞行速度和位置：

根据生物学机理可知，在搜寻猎物过程中，蝙蝠初始阶段发出的超声波脉冲音强大而频率低，有助于在更广泛的空间搜索，发现猎物后，就逐渐减小脉冲音强，同时增加脉冲发射次数，以利于精确掌握猎物的空间位置，用式（4）和（5）来模拟这种搜索特点。

算法1 Bat Algorithm

初始化蝙蝠种群位置xi(i=1，2，…，n)和速度vi

初始化频率 fi，脉冲发生率ri，音量Ai

While（t＜最大迭代次数）

通过调整频率产生新的解

根据式（1）～（3）更新速度和位置

if（rand＞ri）

从最优解集中选一个解

在选择的最优解周围产生一个局部解

end if

通过随机飞行得到一个新解

if（rand＜Aif(xi)＜f(x*)）

接受这个新解

增大 ri，减小 Ai（根据式（4）、（5）调整）

end if

排列蝙蝠并找到当前最优解

end while

3 精英反向混沌蝙蝠算法

3.1 精英反向学习

反向学习（Oppositition-based Learning，OBL）是计算智能中的一个新概念，已经被证明是提高随机搜索算法的搜索能力的一种有效方法［18］。OBL的基本思想是同时评估当前解与反向解，选择较好的解作为下一代的个体，该策略能够有效地提高群体的多样性，避免算法陷入局部最优。

依据概率学原理，每个随机产生的候选解相比它的反向解有50%的概率远离问题最优解［19］。由于全局最优蝙蝠（即精英蝙蝠）是种群的引领者，一旦陷入局部最优，将导致算法进入“早熟”状态。而对蝙蝠进行反向学习将会在很大程度上避免此现象。此外，反向学习带有一定的盲目性，加入精英策略，选择精英个体，进行反向学习，充分利用其特征信，在不过分增加计算量的基础上，加快算法收敛速度。

3.2 混沌蝙蝠算法

混沌目前尚无严格定义，一般将有确定性方程得到的基本有随机性运动状态称为混沌。Logistic映射就是一个典型的混沌系统，迭代公式如下：

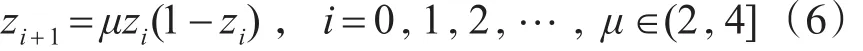
式中，μ为控制参量，当 μ=4 ，0≤z0≤1时Logistic完全处于混沌状态。本文将利用μ=4时的混沌特性，取式（6）的Logistic映射为混沌信号发生器。

基于混沌的蝙蝠算法对基本蝙蝠算法主要有两方面的改进。首先是利用混沌的遍历性，产生初始群体：随机产生一个 d维向量 z1=(z11，z12，…，z1d)，且 z1i∈[0，1] ， i=1，2，…，d ，根据式（6）迭代生成 z2，z3，…，zn，将 zi，i=1，2，…，n 的各个分量载波到优化变量的取值范围：xij=Lb+(Ub-Lb)zij，i=1，2，…n ， j=1，2，…，d 作为初始种群。

其次，在迭代过程中，对蝙蝠位置进行混沌扰动：随机产生一个 d 维向量 u0=(u01，u02，…，u0d)，且 u0i∈[0，1] ， i=1，2，…，d ，根据式（6）迭代生成（t表示迭代次数）作为扰动变量，用

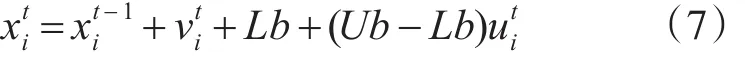
代替蝙蝠的位置更新公式，即式（3）。

3.3 精英反向混沌蝙蝠算法

对于随机优化算法而言，探测能力和开发能力是最受关注的两个问题。本文利用混动扰动策略扩大搜索区域，增加种群多样性，避免陷入局部极值，提高算法的探测能力。但是混沌扰动策略必将在一定程度上减缓算法的收敛进程。而精英反向学习策略可有效地克服这一缺点，加快算法的收敛速度。算法描述如下：

算法2 EOCBA

执行混沌及反向学习策略初始化蝙蝠种群位置xi(i=1，2，…，n)和速度 vi

初始化频率 fi，脉冲发生率ri，音量Ai

While（t＜最大迭代次数）

If（rand＜p）

从当前种群中选择m个最好个体作为精英种群，进行反向学习，形成较优的下一代种群

else

通过调整频率产生新的解

根据式（1）、（2）、（7）更新速度和位置

if（rand＞ri）

从最优解集中选一个解

在选择的最优解周围产生一个局部解end if

通过随机飞行得到一个新解

if（rand＜Aif(xi)＜f(x*)）

接受这个新解

增大 ri，减小 Ai（根据式（4）、（5）调整）end if

排列蝙蝠并找到当前最优解

end if

end while

4 实验与结果分析

为验证本文提出的基于权重策略的蝙蝠算法的性能，选取8个标准测试函数（见表1）进行仿真测试，并与基本算法对比。

4.1 测试函数与试验参数设置

蝙蝠算法中各参数取值尚无理论依据，本文所设置的参数值是根据经验值来确定。基本蝙蝠算法中，种群规模N=30，个体i的最大脉冲频度，最大脉冲音强A=0.75，脉冲音强衰减i系数α=0.9，脉冲频度增加系数γ=0.04，最大迭代次数Nmax=1000，寻优精度ε=10-5。在基于精英反向学习的混沌蝙蝠算法中，精英种群m=10，其余同上。测试函数如表1所示。

表1 标准测试函数

4.2 测试结果与分析

为克服算法的偶然性误差，对每个测试函数，算法分别独立运行30次，图1～8为本文改进算法（EOCBA）与基本蝙蝠算法（BA）对8个测试函数的进化曲线对比。算法性能统计结果见表2。

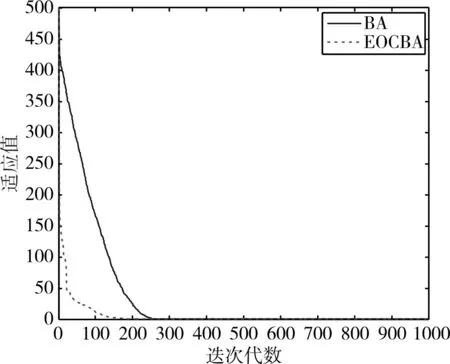
图1 函数 f1的数值进化曲线

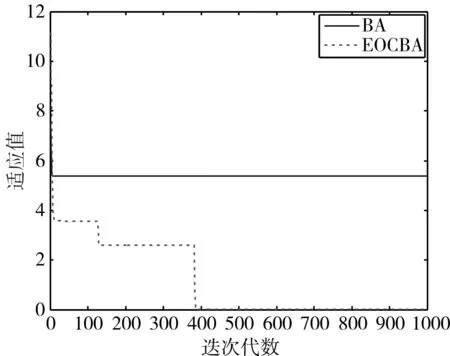
图2 函数 f2的数值进化曲线

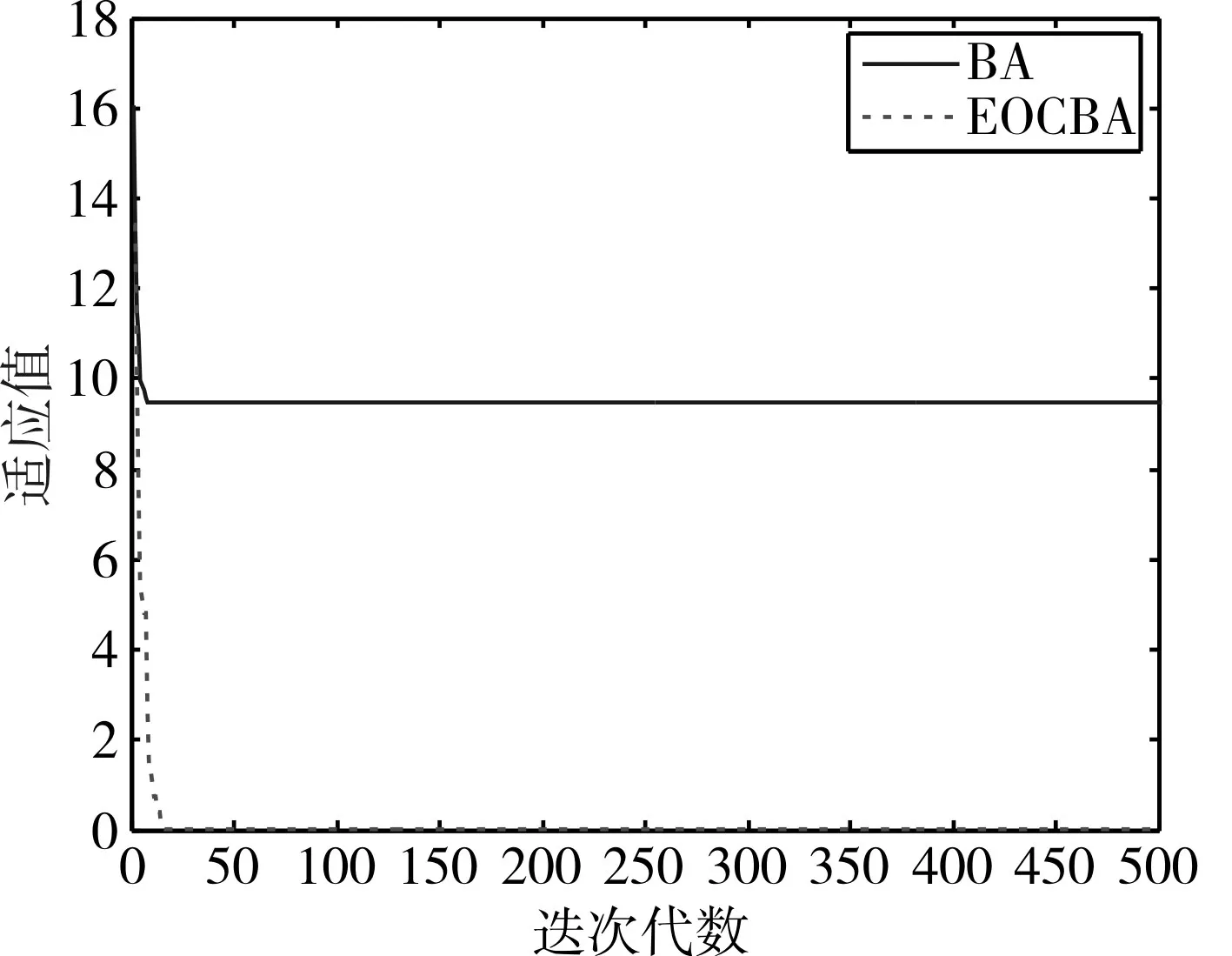
图3 函数 f3的数值进化曲线

图4 函数 f4的数值进化曲线

图5 函数 f5的数值进化曲线

图6 函数 f6的数值进化曲线

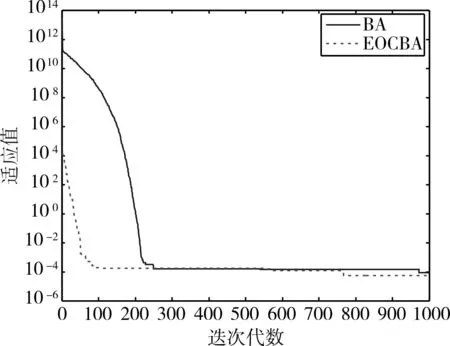
图7 函数 f7的数值进化曲线

图8 函数 f8的数值进化曲线

表2中最优结果、平均结果及最差结果反映了BA和EOCBA对测试函数 f1～f8所求解的质量，改进的算法均优于原算法，特别是对测试函数 f1、f3、f4、f5、f6。标准差反映算法的稳定性，除 f2外，EOCBA均有较明显优势。而对 f2而言，30次测试BA算法均陷入一个局部极值，从而标准差极小，这并不能说明算法性能优越，而属于“早熟”现象。寻优成功率指算法达到寻优精度的次数占实验总次数的比重，是算法性能比较的又一重要指标，除测试函数 f2、f8外，寻优成功率均有所提高，特别是对 f3～f6。平均迭代次数体现算法的寻优速度，EOCBA在收敛速度上快于BA。

改进的算法在寻优精度、寻优成功率和收敛速度方面均有所提高。算法性能的改善主要源于混沌扰动以及精英反向学习保持了种群多样性，同时，精英反向学习充分利用精英蝙蝠的特征信息，以较小的计算量为代价，加快了算法收敛速度。

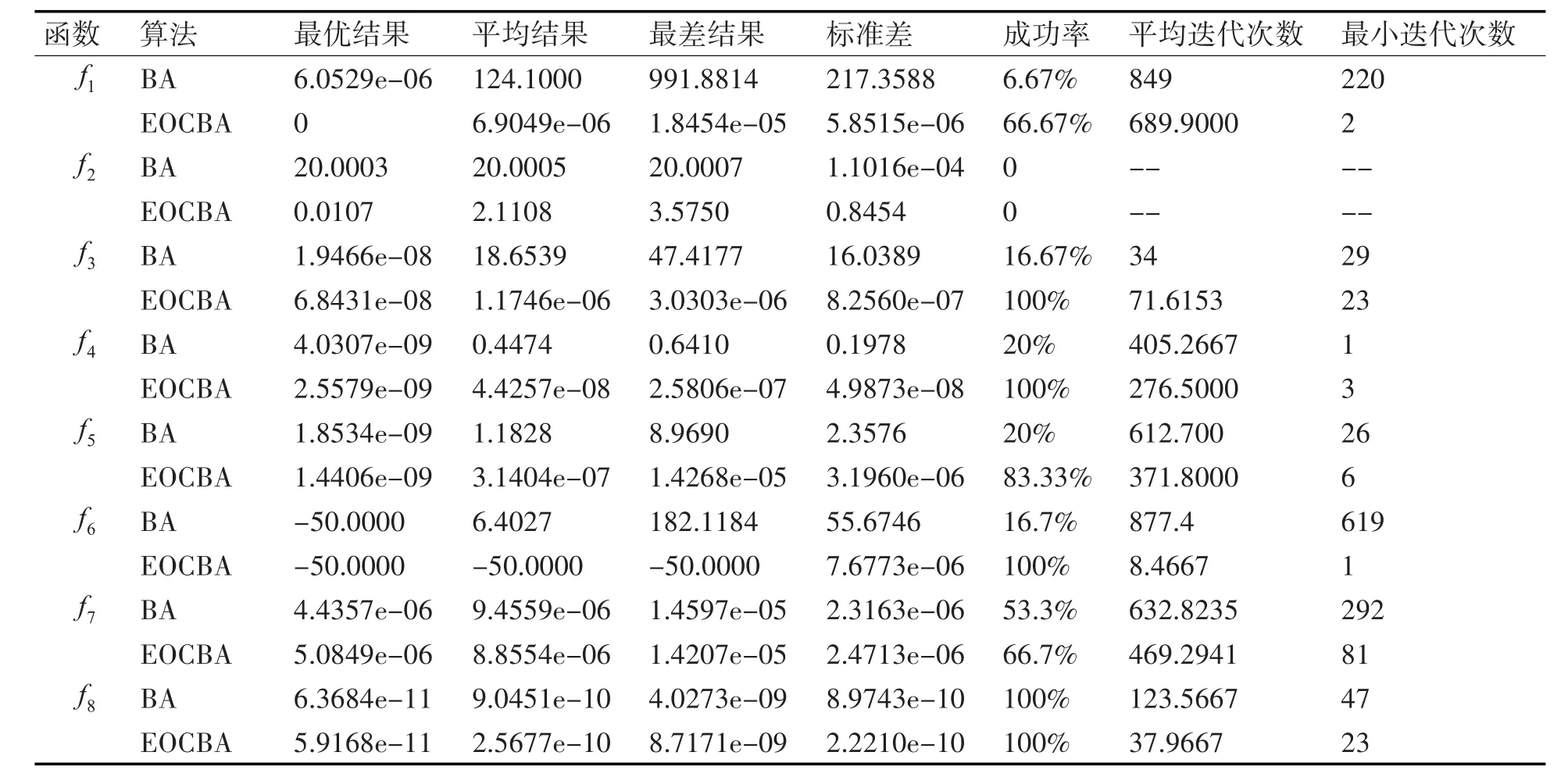
表2 实验结果对比

5 结语

针对基本蝙蝠算法存在的后期收敛速度慢、易陷入局部极值的缺点，该算法引入精英反向学习策略，优化迭代种群，同时，在迭代中对蝙蝠位置进行混沌扰动，增加种群多样性，有效地提高了算法的全局搜索能力和搜索精度。但改进的算法在一定程度上增加了算法复杂度，对混沌映射及精英种群的合理选取，并将新算法用于解决实际问题，将是下一步的研究工作。