2018年高考物理估算题赏析

(湖北省十堰市郧阳中学，湖北 十堰 442000)

估算题是一种特殊类型的考试题型,命题者注重物理知识与科技前沿和生活实际相结合,注重物理规律与思维训练、能力培养相结合,能较好地考查考生的综合分析、发散思维、物理建模、数值计算和应用物理知识解决实际问题等方面的能力,近年来在高考试题中屡见不鲜。

最经典的估算题莫过于1984年全国高考卷中“估算地球大气层的总重力(最后结果取一位有效数字)”,不含提示语,全题11个字,无任何数据信息。显然,物理问题的估算不纯粹是一种数学计算,往往需要综合分析题意,建立物理模型,依据物理规律,对所求物理量的单位、数值和数量级进行定性或半定量的分析、计算,求解分析的关键在“理”，而不在“数”,不追求计算结果的精确,更侧重考查思维方法等。

纵观2018年高考全国卷和地方卷,涉及的物理问题估算题型大致可分为四类，分别举例说明。

1 联系实际,用物理常识近似处理

这类估算题的物理情境比较清晰,未知量与已知量之间的联系比较直观,分析计算过程需要用到一些生活常识和数学常识。如一般高中学生质量约为50～60kg,一个鸡蛋的质量约为50g;楼层高度约为3m,成年人身高约为1.7m等，数学常识方面要特别注意与圆有关的知识。

例1(2018年全国卷II)：高空坠物极易对行人造成伤害。若一个50g的鸡蛋从一居民楼的25层坠下,与地面的碰撞时间约为2ms,则该鸡蛋对地面产生的冲击力约为( )。

A. 10N B. 102N

C. 103N D. 104N

例2(2018年江苏卷)：火车以60m/s的速率转过一段弯道,某乘客发现放在桌面上的指南针在10s内匀速转过了约10°。在此10s内,火车( )。

A． 运动路程为600m

B． 加速度为零

C． 角速度约为1rad/s

D． 转弯半径约为3.4km

2 建构模型,用物理规律定量估算

这类估算题的物理情境比较新颖,有时提供的有用信息较少，甚至不提供任何数据；有时提供大量的干扰信息,未知量与已知量之间的联系比较隐蔽,分析计算过程往往需要充分发挥想象力,挖掘隐含条件,抓住关键因素,合理建立联系未知量和已知量的物理模型,再结合物理规律进行估算。天体运行模型、能量辐射模型、流体模型等是这类估算题中的常见模型。

例3(2018年全国卷I)：2017年,人类第一次直接探测到来自双中子星合并的引力波。根据科学家们复原的过程,在两颗中子星合并前约100s时,它们相距约400km,绕二者连线上的某点每秒转动12圈。将两颗中子星都看作是质量均匀分布的球体,由这些数据、万有引力常量并利用牛顿力学知识,可以估算出这一时刻两颗中子星( )。

A． 质量之积

B． 质量之和

C． 速率之和

D． 各自的自转角速度

解析：结合天体运行模型，综合考查万有引力定律、圆周运动知识和估算能力是历年高考的热点。本题以人类首次发现双中子星合并产生引力波事件为背景，考查万有引力知识,将最新的科学研究成果与基础物理知识相结合。区别于一般的天体运行试题,本题虽然给出了天体运行的一些数据,但不要求进行具体的数值计算,解题的关键是依据题意建立双中子星合并前的双星运行模型,再进行分析讨论。

例4(2018全国卷II)：2018年2月,我国500m口径射电望远镜(天眼)发现毫秒脉冲星“J0318+0253”,其自转周期T=5.19ms。假设星体为质量均匀分布的球体,已知万有引力常量为6.67×10-11N·m2/kg2。以周期T稳定自转的星体的密度最小值约为( )。

A． 5×109kg/m3

B． 5×1012kg/m3

C． 5×1015kg/m3

D． 5×1018kg/m3

在求解天体运行类型的估算题时,重点关注估算数量级的准确性,计算时可对常见数据做近似处理,如π2≈10,地球公转周期T=365天=3.15×107s≈π×107s,与地球半径有关的数据6.42≈40等,这样会很快得出最终结果。

3 数形结合,用图像信息定性讨论

这类估算题的物理情境比较常见,叙述的物理情景往往配有一幅示意图或是函数图像,通过图形、图像来展示物理过程和呈现物理量之间的相互关系。分析这类问题,不仅要弄清楚图像本身的含义和图像所表明的函数关系,还要弄清楚图像中的点、线、斜率、截距、面积等的物理意义。

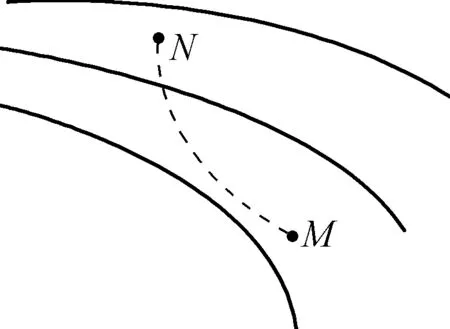
图1

例5(2018年天津卷)：如图1所示,实线表示某电场的电场线(方向未标出),虚线是一带负电的粒子只在电场力作用下的运动轨迹,设M点和N点的电势分别为φM、φN,粒子在M和N时加速度大小分别为aM、aN,速度大小分别为vM、vN,电势能分别为EpM、EpN。下列判断正确的是:( )。

A．vM

B．vM

C．φM<φN,EpM

D．aM

解析：静电场中常用电场线、等势面来描绘电场的分布情况,电场线某点的切线方向表示场强方向,电场线和等差等势面的疏密表示场强相对大小。N处附近电场线较为密集,粒子在N处所受电场力较大,加速度aMvN,电势能EpMφN。选项D正确。

每一个物理过程都满足一定的物理规律,每一个物理规律都可以表示成一种函数关系,每一种函数关系都对应着一个函数图像,而每一个函数图像则都通过图像的几何特征展示着复杂的物理过程和物理规律,这正是数形结合的具体体现。

4 理论分析,运用物理方法综合判断

这类估算题的物理情境比较少见,与平时解题涉及的理想化物理情境有所区别,比如定滑轮质量不能忽略、带电体不能视为点电荷等,用常规方法无法直接求解,往往需要综合利用对称性、守恒量、量纲分析、特殊值法或是极限分析等物理思维方法进行定性讨论和分析判断。

例6(2018年北京卷)：根据高中所学知识可知,做自由落体运动的小球,将落在正下方位置。但实际上,赤道上方200m处无初速下落的小球将落在正下方位置偏东约6cm处。这一现象可解释为,除重力外,由于地球自转,下落过程小球还受到一个水平向东的力,该“力”与竖直方向的速度大小成正比。现将小球从赤道地面竖直上抛,考虑对称性,上升过程该“力”水平向西,则小球( )。

A． 到最高点时,水平方向的加速度和速度均为零

B． 到最高点时,水平方向的加速度和速度均不为零

C． 落地点在抛出点东侧

D． 落地点在抛出点西侧

解析：本题考察的运动情境为抛体运动,但区别于理想的竖直上抛运动,小球上升和下降过程不仅要考虑重力,还要考虑水平方向的“力”——科里奥利力。上升阶段,小球受到水平向西的“力”,水平方向向西做加速运动,至最高点时有水平向西的速度和竖直向下的重力加速度;下降阶段,小球受到水平向东的“力”,水平方向向西做减速运动至落地点,由对称性可知水平速度恰好减为零,故落地点应在抛出点西侧,选项D正确。

回顾历年全国和地方高考卷面中不同形式的估算题可发现,分析求解估算题有规律可循,关键有三步：第一步,综合分析题意,建立物理模型;第二步,依据物理规律,建立联系方程;第三步,合理取舍数据,近似计算分析。其中，分析求解过程注重定性与定量结合,常常要用到对称分析、量纲分析、极限分析、特例讨论、常识常数、近似计算等方法。当然,估算作为一种常用的科学思维和计算方法,生活中有很强的实用性,我们作为教师,对估算题的教学着眼点不仅要落实在解题步骤和分析方法的总结、传授上,更要落实在思维方式和核心素养的培养上,这也正是新课标、新教材和新高考积极倡导的改革方向。