数学方法在高中运动学问题解决中的应用①

(湖南省岳阳市第一中学，湖南 岳阳 414000)

在新课标理综(物理)考试大纲中,对于运用数学方法处理物理问题的能力有明确说明:能够根据具体问题列出物理量之间的关系式,进行推导和求解,并根据结果得出物理结论;能运用几何图形、函数图像进行表达、分析。下文将通过几道经典的运动学例题,探讨数学方法在物理问题解决中的应用。

1 用定积分巧解变加速运动中的时间问题

例1：假设小球在空气中下落过程受到的空气阻力与球的速率成正比,即f=kv,比例系数k决定于小球的体积,与其他因素无关,让体积相同而质量不同的小球在空气中由静止下落,它们的加速度与速度的关系图像如图1所示,则( )。

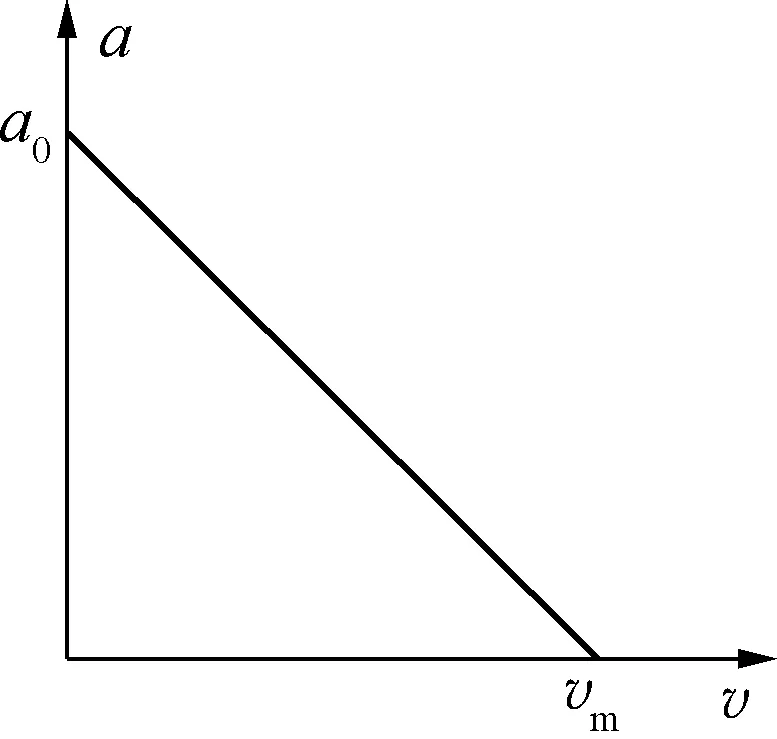
图1

A. 小球的质量越大,图像中的a0越大

B. 小球的质量越大,图像中的vm越大

C. 小球的质量越大,速率达到vm时经历的时间越短

D. 小球的质量越大,速率达到vm时下落的距离越长

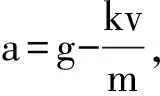
(1) 当v=0时,a=a0=g,与小球的质量无关,A选项错误。

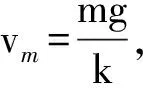
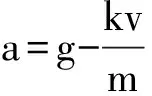
评析:本题C、D选项还可以利用a-t图像,v-t图像进行定性讨论,在此不展开讨论。利用积分的方法,无限逼近最大速度,解决了运动时间问题,将“速度变化量是加速度对时间的定积分,加速度是速度对时间的求导”的关系体现出来。

2 利用一元二次函数和不等式的特点巧解追及与相遇问题

2.1 利用对称轴求最值

例2:一辆汽车在十字路口等待绿灯,当绿灯亮时汽车以a=3m/s2的加速度开始行驶,恰在这时一人骑自行车以v0=6m/s的速度匀速驶来,从后边超过汽车,试问:汽车从路口开动后,在追上自行车之前经过多长时间两车相距最远?最远距离是多大?

图2

本例利用一元二次函数解决追及相遇中的最大距离的问题,将物理情景转化到学生熟悉的数学函数,帮助学生理解相距最远时速度应该满足的条件。

2.2 利用判别式求满足条件的范围

例3:甲、乙两车在同一直线轨道上同向行驶,甲车在前,速度为v1=8m/s,乙车在后,速度为v2=16m/s,当两车相距x0=8m时,甲车因故开始刹车,加速度大小为a1=2m/s2,为避免相撞,乙车立即开始刹车,则乙车的加速度至少为多大?

本例利用一元二次不等式来解决不相撞的临界条件,根据判别式小于零使得不等式恒成立,从而求出加速度范围。

3 用基本不等式快速求解最值问题

例4:一水池水深H=0.8m，现从水面上方h=0.8m高处由静止释放一质量为m=0.1kg的硬质球体,测得球体从释放到落至水池底部用时t=0.6s。已知球体直径远小于水池深度,不计空气及水的阻力,取g=10m/s2。

(1) 通过计算判断球体在水中运动的性质。

(2) 从水面上方多高处静止释放小球,才能使小球落至池底所用时间最短?

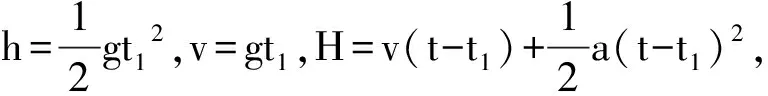
应用基本不等式来求解高中物理问题很常见。本例的第(2)问是一个比较复杂的物理问题,通过基本不等式的求解,直接简化了物理模型的构建,可以比较快速地将最值问题解决。