新生儿万古霉素血药谷浓度影响因素分析
2019-05-05唐喆曹静帅维维陈小慧韩树萍
唐喆 曹静 帅维维 陈小慧 韩树萍
(南京医科大学附属妇产医院,南京市妇幼保健院,南京 210004)
万古霉素属于三环糖肽类抗生素,对革兰阳性菌具有强大的抗菌活性,常应用于新生儿重症监护室(NICU),用于治疗革兰阳性菌所致的严重感染。万古霉素具有肾毒性和耳毒性,对新生儿尤其应谨慎使用,避免血药浓度过高,防止不良反应发生。如果万古霉素治疗浓度过低,容易诱导产生耐药菌,导致治疗失败。因此,万古霉素应用于新生儿时必须进行血药浓度监测,并根据监测结果及时调整万古霉素剂量[1-3]。
《美国感染病学会万古霉素治疗指南》和《万古霉素临床应用中国专家共识》(以下简称《共识》)建议,在使用万古霉素进行抗感染治疗时,其稳态谷浓度应维持在10μg/mL以上,治疗重症感染时应达到15~20μg/mL[4-5]。相关报道显示,新生儿万古霉素谷浓度在多数情况下普遍偏低,达标率不高,增加了诱导产生耐药菌的风险[6-7]。临床药师在血药浓度监测过程中还发现,仅通过肾功能或者体重拟定给药剂量并不能保证万古霉素血药浓度达标率,可见谷浓度是否能够达到《共识》推荐范围还受其他诸多因素的影响[8-9]。
影响新生儿万古霉素血药浓度的因素众多,如患儿体重、胎龄、日龄、肝肾功能、给药方案等,仅依靠单因素分析常不能控制诸多变量间的混杂因素,难以得到具有统计学意义的结果[10]。多元线性回归能够有效控制自变量间的混杂因素,通过以新生儿万古霉素谷浓度作为因变量,影响谷浓度的因素为自变量,建立多元线性回归模型,可识别出对谷浓度有显著影响的因素,并根据所建模型,进一步估算各影响因素的相对重要性,从而判明限制谷浓度达标率的原因。目前通过多元线性回归分析新生儿万古霉素谷浓度影响因素的报道较少,分析时纳入的自变量个数有限,未建立回归模型,也未利用回归模型估算各影响因素的相对重要性,临床指导意义有限[11]。
本次研究旨在建立多元线性回归模型,分析影响新生儿万古霉素血药浓度的诸多因素,并估算各因素相对重要性,以探求血药浓度达标率普遍偏低的原因,提高血药浓度达标可能性,为医师调整给药方案提供参考。
1 资料与方法
1.1 入选标准
纳入研究对象均为南京市妇幼保健院新生儿科收治的重症感染患儿且患儿经医师确认需使用万古霉素进行抗感染治疗,并满足以下要求:纳入研究时为首次应用万古霉素;纳入研究时患儿无明显脏器功能损害表现,如肾衰竭、肝功能损害等;纳入研究的血药浓度值为初次监测谷浓度时所得,监测前给药方案未进行调整;监测时万古霉素给药已达3或4个维持剂量(达稳态血药浓度),在下次给药前30min内采血;临床资料和各项检验数据完整。
排除对象:纳入研究前已使用过万古霉素进行治疗;未按规定时间采集血药浓度或监测时血药浓度未达到稳态;无法收集到完整资料的病例。
1.2 资料来源
选取2016年1月—2017年12月在我院儿科重症监护室使用万古霉素进行抗感染治疗的新生儿病例进行回顾性分析,根据入选标准(“1.1”项),入选病例为107例。收集患儿的各项指标,作为用R软件建立多元线性回归模型的数据来源,具体内容包括:①万古霉素谷浓度(C);②给药方案:单次给药剂量(Dose)、给药间隔(Tau);③人口学:日龄(PNA)、矫正体重(WT)、性别(SEX)、身高(HT)、矫正胎龄(PMA);④肾功能:尿素(U)、血肌酐(Cr)、肌酐清除率(CLCR);⑤肝功能:白蛋白(ALB)、丙氨酸氨基转移酶(ALT)、天冬氨酰氨基转移酶(AST)、总胆红素(TBIL);⑥是否接受静脉营养治疗;⑦是否使用呋塞米。其中矫正体重为谷浓度采集当天患儿体重,矫正胎龄为谷浓度采集当天患儿日龄加患儿胎龄。呋塞米为强效利尿药,临床常用于治疗危重患儿的水肿性疾病,万古霉素主要经肾脏排泄,呋塞米的使用可能干扰万古霉素的体内清除从而影响万古霉素谷浓度,故将之纳入研究。CLCR利用Schwartz公式(公式1)计算,具体公式如下[12]:
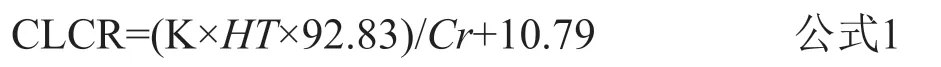
CLCR:肌酐清除率[单位:(mL/min)/1.73m2];K:矫正因子,0.45(小于1岁足月儿)或0.33(小于1岁的早产儿);HT:身高(单位:cm);Cr:血肌酐(单位:μmol/L)。
1.3 检测方法
利用高效液相色谱法(HPLC)监测患儿万古霉素血药浓度。该方法已通过方法学验证[13]。由于患儿治疗期间同时使用多种药物进行治疗,为避免潜在干扰,本法采用外标法。万古霉素与内源性物质分离完全,不受合并用药干扰,线性良好,线性范围为2.0~50.0μg/mL,回收率和精密度符合生物样本的测定要求。检测时每次使用乙二胺四乙酸(EDTA)抗凝管取患儿全血1mL,离心后所得血浆样本置于4℃冰箱内待测。取血后24h内完成样本检测。
1.4 仪器与试剂
Waters高效液相色谱仪(1525泵,2487紫外检测器,2707自动进样器,Empower 3色谱工作站)。万古霉素标准品(中国食品药品检定研究院,批号:130360-201302,纯度:99.2%);色谱纯:甲醇(美国Tedia公司)、乙腈(国药集团化学试剂有限公司);分析纯:磷酸二氢钾、高氯酸、磷酸,均由国药集团化学试剂有限公司生产;注射用水(安徽双鹤药业)。
1.5 药品及器械信息
万古霉素由日本Eli Lilly Japan K.K.公司生产,注册证号:H20080356,规格:0.5克/瓶。微量静脉泵由北京通盛易达医疗科技有限公司生产,型号:BYZ单通道。
1.6 给药方案
具体给药剂量根据临床实际情况,参照万古霉素说明书,按新生儿的胎龄及体质量确定剂量后,每天分次通过微量静脉泵给药,每次给药持续时间为1h。
1.7 统计学方法
使用R软件(R3.4.1)进行统计学分析。
1.7.1 变量的定义与赋值定义
因变量为血药浓度值,其余变量定义为自变量。由于临床指标数值多数不符合正态分布,故统计时将连续型变量(包括血药浓度值、单次给药剂量、给药间隔、日龄、矫正胎龄、矫正体重、尿素、血肌酐、肌酐清除率、白蛋白、丙氨酸氨基转移酶、天冬氨酰氨基转移酶、总胆红素)均转化为实测值的10底对数纳入研究。对分类变量(包括性别、是否接受静脉营养治疗、是否使用呋塞米)进行赋值,利用as.factor()函数转化为因子型变量纳入研究。各因素的单位、缩写、赋值见表1。对赋值后的各变量进行单因素线性回归分析,进行自变量筛选。
1.7.2 单因素线性回归分析
通过单因素线性回归分析,依次考察因变量和不同自变量之间的相关性。如所得P<0.25,则认为该自变量与因变量间可能存在潜在相关性,应纳入多元线性回归方程进一步分析[14]。
1.7.3 多元线性回归分析
将单因素线性回归分析后筛选出的自变量纳入多元回归方程,依据赤池信息准则(AIC),利用后退逐步回归法进行模型拟合,以得到最优模型。运用R软件中的lm()函数建立回归方程,利用MASS包中的stepAIC()函数执行后退逐步回归。对模型的正态性、误差的独立性、线性、方差齐性进行考察,并判断自变量之间是否存在多重线性。利用car包中的qqPlot()函数,直接生成模型的学生化残差,绘制分位数比较图,考察模型正态性;利用Durbin-Watson检验(durbinWatsonTest()函数)判别因变量值是否相互独立,P<0.05时可判断因变量之间相互不独立,呈自相关性;利用summary()函数查看回归方程F检验结果,P<0.05时可判断方程线性关系显著;利用rstandard()函数计算回归模型的标准化残差,利用plot()函数绘制标准化残差图,查看回归方程方差齐性;使用vif()函数计算膨胀因子(VIF),当VIF>5时,即认为自变量间存在多重共线性[15]。回归系数P<0.05时为差异有统计学意义,即剔除该回归项会对方程造成显著影响。通过绘制拟合图、计算绝对偏差(公式2)和个体相对偏差(公式3)评价模型拟合效果。绘制Bland-Altman分析图评价预测结果与实测结果的一致性。
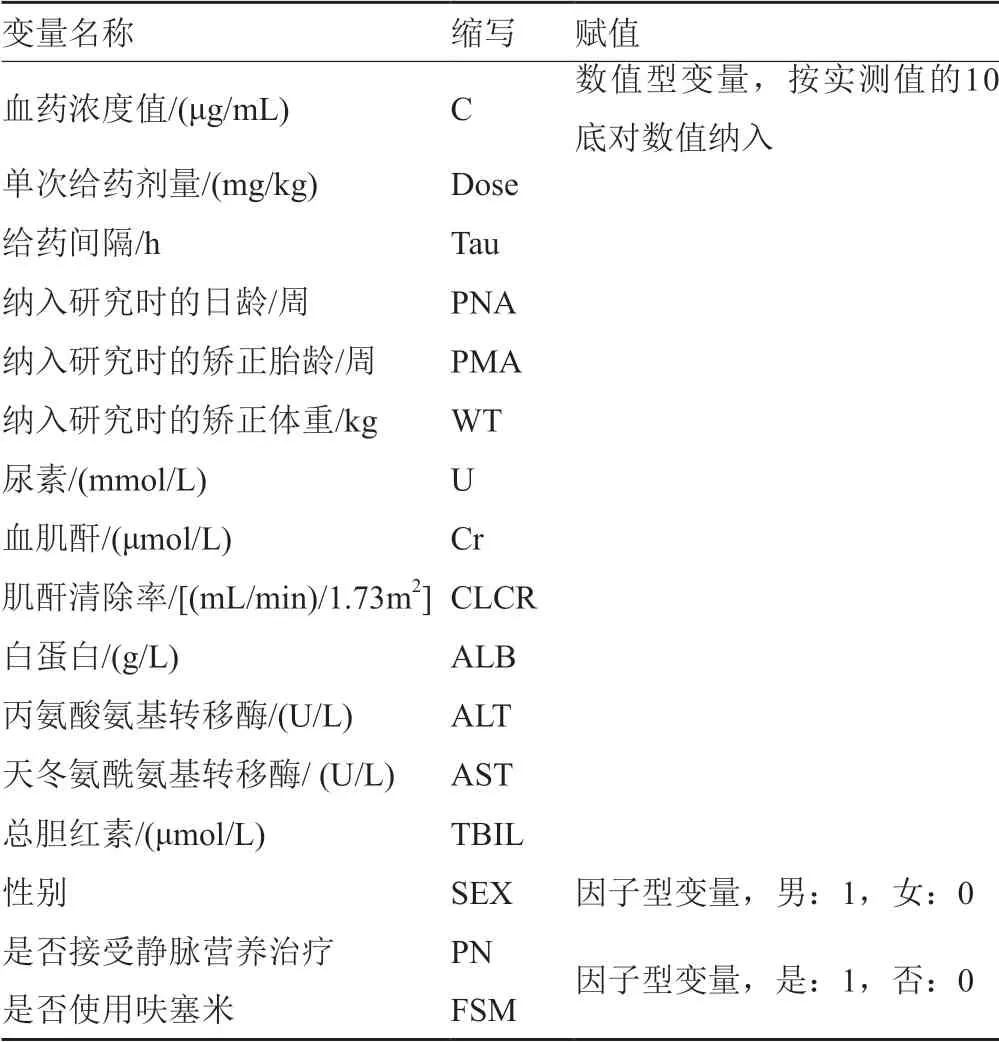
表1 各变量的单位、赋值、缩写Tab.1 Units,specific quantitative values and abrrevation of variables

相对重要性计算相对重要性法由Johnson于2000年提出,是一种评价自变量对因变量贡献大小的新方法。相对重要性法分别通过原始变量对正交变量、因变量对正交变量建立线性回归方程,自变量的相对重要性为两组回归系数平方的积和。与传统的标准回归系数法相比,相对重要性法利用正交转换消除自变量间相关性的影响,较传统方法更为可靠。本次研究利用JM LeBreton所编代码,根据多元线性回归分析所得最优模型,对自变量的相对重要性进行计算,评价自变量对因变量的影响程度,具体代码见图1[16]。

图1 相对重要性计算代码Fig.1 Code for calculating relative importance
1.7.4 分组比较
根据谷浓度是否达到《共识》推荐范围下限,即10μg/mL[4-5],将纳入研究患儿分为两组。参照优化后的多元线性回归模型,利用Mann-Whitney U检验,比较两组患儿的基本特征差异。
2 结果
2.1 患儿的基本情况
本次研究共纳入符合标准的患儿107例,男62例,女45例, 其中早产儿84例,足月儿23例。患儿基本情况见表2,详细个体信息见附表1。临床第一诊断为新生儿败血症51例,新生儿坏死性小肠结肠炎19例,新生儿肺炎15例,新生儿化脓性脑膜炎12例,其他诊断10例。接受静脉营养治疗的患儿75例,未接受者32例。测定谷浓度前使用呋塞米治疗的患儿22例,未使用者85例。
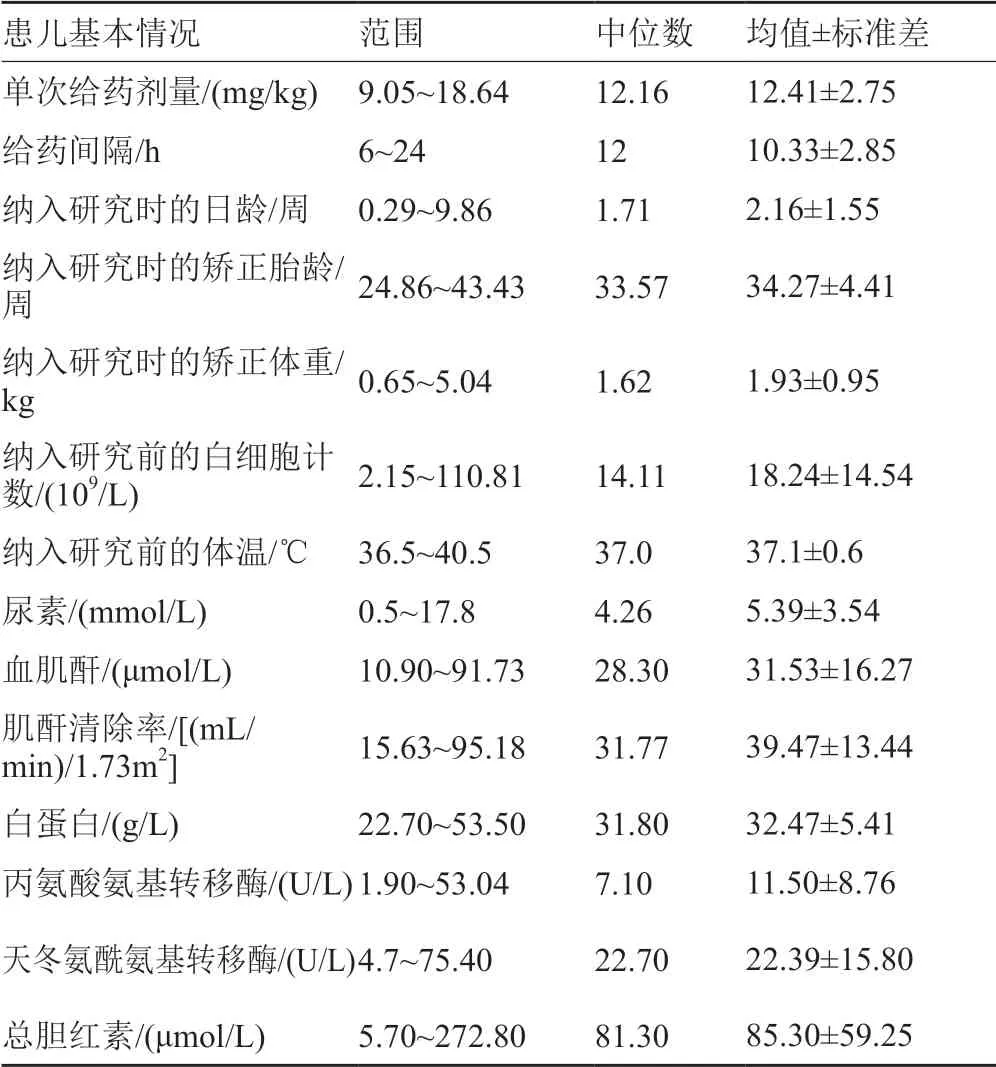
表2 患儿基本情况(n=107)Tab.2 Baseline characteristics of patients (n=107)
2.2 血药谷浓度监测结果
从表3可知患儿血药谷浓度的监测结果。绝大部分患儿的谷浓度均在20μg/mL以下,可见在临床经验治疗情况下,只有极少数患儿的谷浓度超出《共识》推荐值上限,患儿用药在大多数情况下安全。57位患儿在监测谷浓度的同时亦监测了峰浓度,患儿谷浓度偏高时峰浓度也相应增高,符合实际情况。有43.93%的患儿谷浓度偏低,未达到10μg/mL,限制了万古霉素的抗感染疗效,也容易诱导耐药的发生。
2.3 病原学检查结果
107例患儿在接受万古霉素治疗前,均进行了病原学检查,结果见表4。80例患儿病原学结果为阳性,12例为混合感染。病原学结果为阴性的患儿有27例。培养与鉴定出致病菌株92例,76例为革兰阳性菌,14例为革兰阴性菌,2例为真菌。病原学检查阳性部位为血液、痰、导管、外耳道和支气管分泌物等。
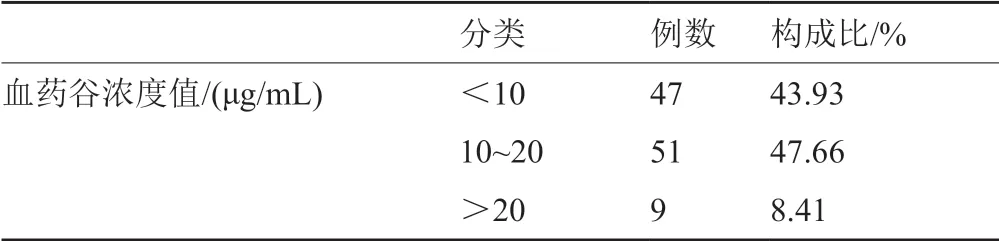
表3 血药谷浓度监测结果Tab.3 The result of trough concentration
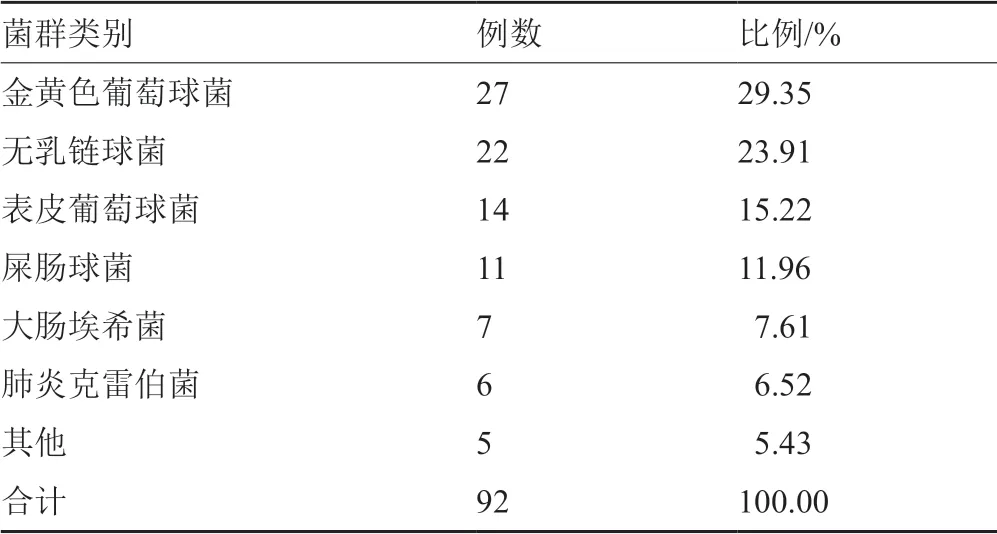
表4 病原学检查结果Tab.4 Results of etiological examination
2.4 单因素线性回归分析
单因素分析结果显示,自变量单次给药剂量、给药间隔、矫正体重、矫正胎龄、血肌酐、肌酐清除率与因变量谷浓度之间有潜在相关性(P<0.25)。肌酐清除率与矫正体重、矫正胎龄、血肌酐均有强相关性,直接引入多元回归方程易引起统计学错误,故剔除。将单次给药剂量、给药间隔、矫正体重、矫正胎龄、血肌酐纳入多元线性回归分析。
2.5 多元线性回归分析
2.5.1 多元线性回归模型
利用lm()函数建立初始回归方程。初始方程的AIC=-178.66。采用后退逐步回归法进行多元线性回归分析后,方程AIC下降到-183.18。4个对因变量谷浓度作用显著的自变量为矫正体重(WT)、单次给药剂量(Dose)、给药间隔(Tau)和血肌酐(Cr)(P<0.05)。应用anova()函数比较初始方程和经后退逐步回归法优化方程的拟合优度,F检验结果不显著(P>0.05),可见后退逐步回归法删除的自变量对方程拟合优度无显著影响。最终所得模型方程为:C=3.28-0.48WT+0.18Cr-1.15Tau+0.55Dose(表5)。回归模型的F检验结果显示方程线性关系显著,P<0.05。
多元线性回归模型的验证各自变量的膨胀因子在1.17~1.81之间,均小于5,多重共线性不显著。经在方程内引入交互项验证,各自变量间无显著交互效应。图2为预测值比实测值的拟合图,预测值与实测值的相关系数为0.52,基本呈直线分布。模型的残差分位数图(Q-Q plot)显示,各点均落于置信区间内,模型符合正态性假设(图3)。利用Durbin-Watson检验判别因变量值是否相互独立,P值不显著(P=0.34),说明因变量间无自相关性,误差相互独立。标准化残差散点图中(图4),绝大部分残差值均分布于[-2,2]的带状区域内,模型满足残差方差齐性的条件。故所建模型满足多元线性回归各项假设。模型的绝对偏差平均值为1.91,95%置信区间为[-0.42,0.42]。个体相对偏差均值为28.98%,95%置信区间为[-6.07%,6.07%]。图5为模型的Bland-Altman分析图,从图中可知,只有少数点落在95%的一致性界线以外,可见预测值和实测值的一致性较好。
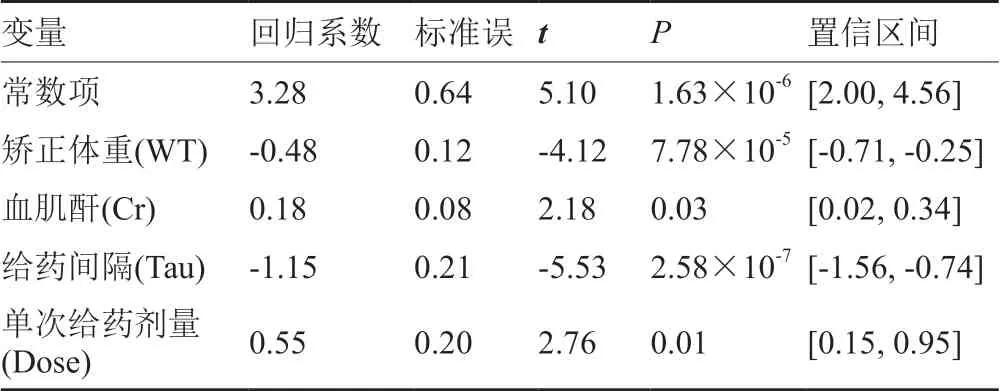
表5 多元回归分析结果Tab.5 Results for multiple linear regression analysis
2.6 相对重要性
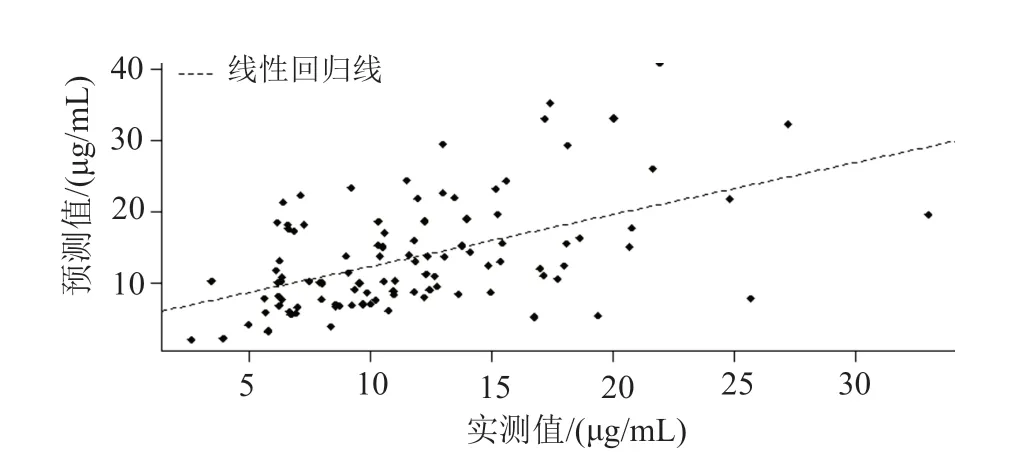
图2 拟合图Fig.2 Plot forfitting
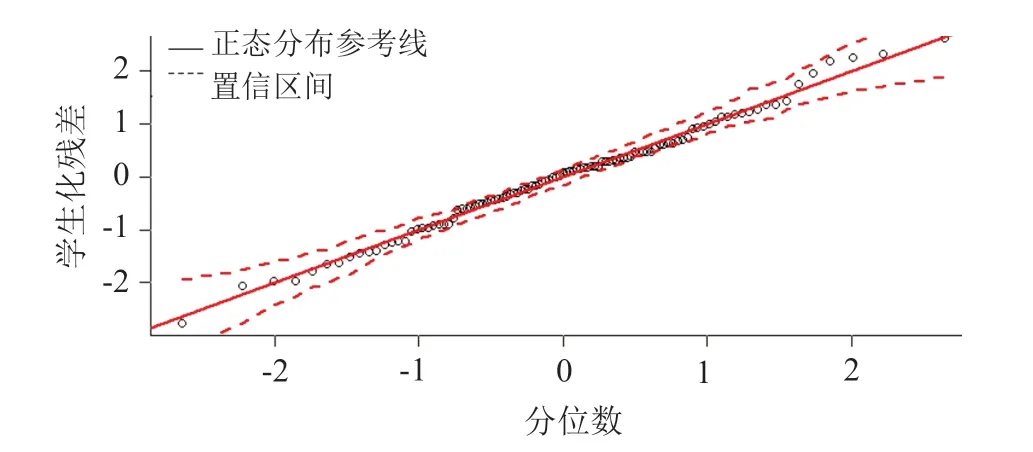
图3 Q-Q plot图Fig.3 Q-Q plot graph
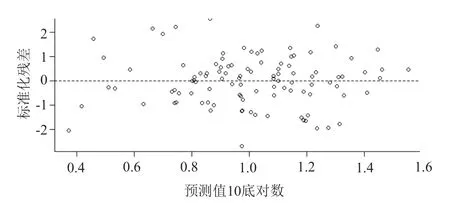
图4 标准化残差图Fig.4 Plot for standardized residual
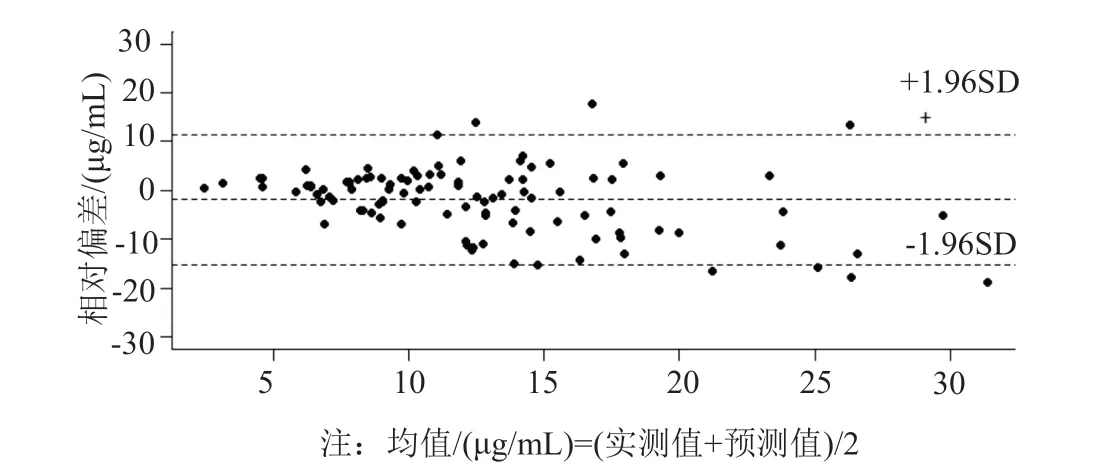
图5 Bland-Altman分析图Fig.5 Plot for Bland-Altman analysis
根据优化后的模型计算各自变量的相对重要性。给药间隔对谷浓度的影响程度最为显著,相对重要性为50.90%。患儿矫正体重、血肌酐值、单次给药剂量的相对重要性分别为27.00%、14.60%和7.50%(图6)。对于血药谷浓度而言,自变量给药间隔有最大的相对重要性,即调整给药间隔能够最大程度影响血药谷浓度。患儿矫正体重和血肌酐值亦对血药谷浓度有较大影响。不同患儿的矫正体重和血肌酐值差异较大,临床医师应根据这两个因素拟定给药方案。相对给药间隔而言,调整单次给药剂量对血药谷浓度影响偏小,只能小幅影响谷浓度。
2.7 分组比较
根据表6结果可知,谷浓度小于10μg/mL与谷浓度大于10μg/mL的患儿矫正体重和血肌酐值无统计学差异。两组患儿的给药间隔和单次给药剂量有显著性差异,谷浓度大于10μg/mL的患儿给药间隔较短,单次给药剂量较大。
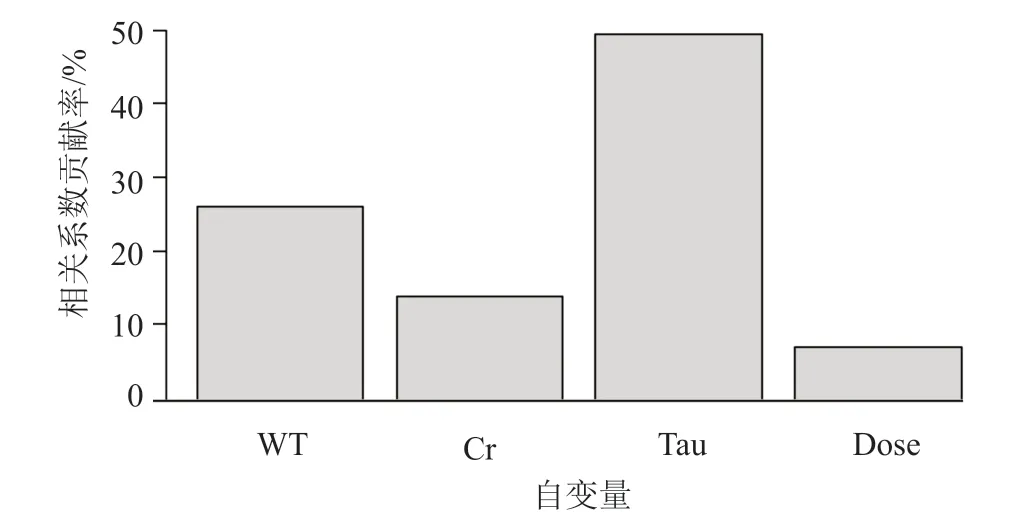
图6 相对重要性Fig.6 Plot for relative importance
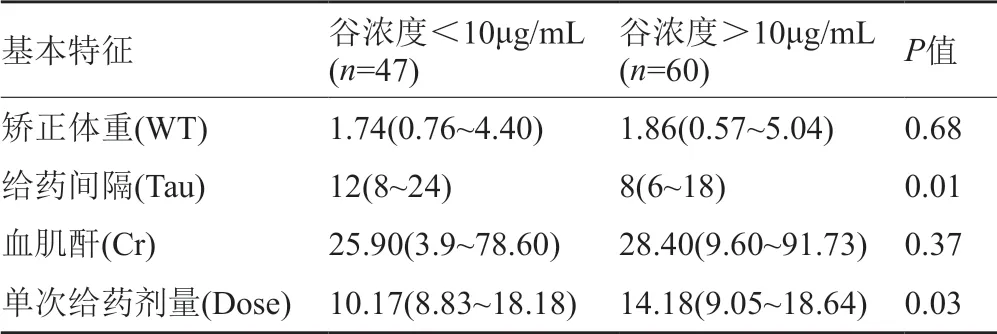
表6 谷浓度<10μg/mL患儿与>10μg/mL患儿的基本特征差异Tab.6 Differences in characteristics of patients who achieved 10μg/mL and those who did not
3 讨论
由表3可知,我院万古霉素血药浓度达标率仅为47.66%,有相当一部分患儿谷浓度不达标,整体谷浓度偏低。以往药动学研究表明,患儿的矫正体重、矫正胎龄、万古霉素日剂量、肾功能等因素均对谷浓度均有明显影响,粗略可知日剂量越大血药谷浓度越高,肾清除率越大,谷浓度越小,但仍无法确定哪种因素对谷浓度影响程度更大[17]。根据多元线性回归模型和相对重要性计算结果,本次研究进一步阐明,给药间隔为影响谷浓度最重要的因素,余下依次是矫正体重、血肌酐值和单次给药剂量。又根据分组比较结果进一步可知,制约谷浓度达标率的主要因素为给药间隔偏长与单次给药剂量偏小。
与给药间隔相比,单次给药剂量对万古霉素谷浓度的影响偏小,可能的原因有:1)万古霉素说明书对新生儿的推荐单次给药剂量为10~15mg/kg,范围较窄,不同患儿接受的单次给药剂量区别不大;2)目前临床上使用的万古霉素为0.5 g包装的粉针剂,患儿单次使用剂量远小于药品包装量,故万古霉素粉针剂需多次稀释后方能使用,繁复的配制过程对单次给药剂量的精确性有潜在影响[18]。
本次研究还表明,血肌酐值是影响万古霉素谷浓度的重要因素,与既往报道一致[19]。万古霉素主要通过肾小球以原形排出体外,因此患儿的肾小球滤过率(GFR)对万古霉素谷浓度有显著影响。考虑到新生儿GFR的计算比较复杂,临床上不易获得[12],而利用Schwartz法得到的内生肌酐清除率(CLCR)与患儿体重有强相关性,引入模型后会造成统计学错误,故本次研究采用血肌酐值来分析其与谷浓度的相关性。患儿血肌酐值与万古霉素谷浓度呈正相关,但相对重要性小于给药间隔与患儿矫正体重。纳入本次研究的患儿多为早产儿,在NICU住院期间存在大量输液与营养不良的现象,导致临床获得的血肌酐值普遍偏低,这可能影响到血肌酐值对万古霉素谷浓度的相对重要性[20]。
LeBreton所建立的相对重要性计算法是一个有前景的新方法,可以有效评价各自变量对因变量的贡献率,比传统的标准化回归系数法更为直观,并且能在模型存在多重共线性和交互效应的情况下,准确计算自变量的相对权重。根据多元线性回归分析结果(表5)可知,各自变量的P值排序为给药间隔<矫正体重<单次给药剂量<血肌酐,各自变量的影响排序即为给药间隔>矫正体重>单次给药剂量>血肌酐。相对重要性结果(图6)排序为给药间隔>矫正体重>血肌酐>单次给药剂量,与多元线性回归分析结果稍有不同。这种差异可能是由于相对重要性计算过程中的原始变量正交变换所导致。过往研究表明,相对权重法确立的重要性排序与传统估计方法得出的结果可能有差异,当传统估计方法与相对权重法估计的结果不同时,鉴于相对权重法的多种特性,应优先采用相对重要性估计的结果[21]。相对重要性计算仍有一定的局限性。相对重要性的计算建立在模型包含所有自变量的基础之上[16,22]。本次研究虽然已筛选多个自变量,但新生儿重症治疗方案极其复杂,临床上潜在影响新生儿万古霉素谷浓度的因素极多,不排除仍有重要自变量未纳入模型进行研究[23]。此外,相对重要性计算仅考察了自变量对因变量的影响程度大小,没有考察影响方向,在解读相对重要性计算结果时仍需参考多元线性回归分析结果中各项系数的正负。
本次研究仅从线性模型角度分析了影响万古霉素血药谷浓度的因素,但药物的体内代谢过程多呈非线性,线性模型不足以准确描述这些复杂情况。线性模型也难以基于不同的体重和血肌酐值直接拟定给药方案。这些问题有待新生儿万古霉素群体药动学研究解决。目前针对中国新生儿的相关研究极少[19],仍有影响万古霉素血药浓度的因素尚未被评估与解释,有待未来进一步研究。
4 结论
新生儿万古霉素谷浓度值与给药间隔、患儿矫正体重、血肌酐值、单次给药剂量有显著相关性。给药间隔对谷浓度的影响程度最为显著,随后依次是患儿矫正体重、血肌酐值和单次给药剂量。制约患儿谷浓度达标率的主要因素是给药间隔偏长、单次给药剂量偏小。与缩短给药间隔相比,增加单次给药剂量增加谷浓度的程度较小。患儿肾功能对谷浓度亦有显著正相关性。考虑到新生儿重症患者治疗的复杂性,其他潜在影响新生儿万古霉素谷浓度的因素仍有待进一步研究。
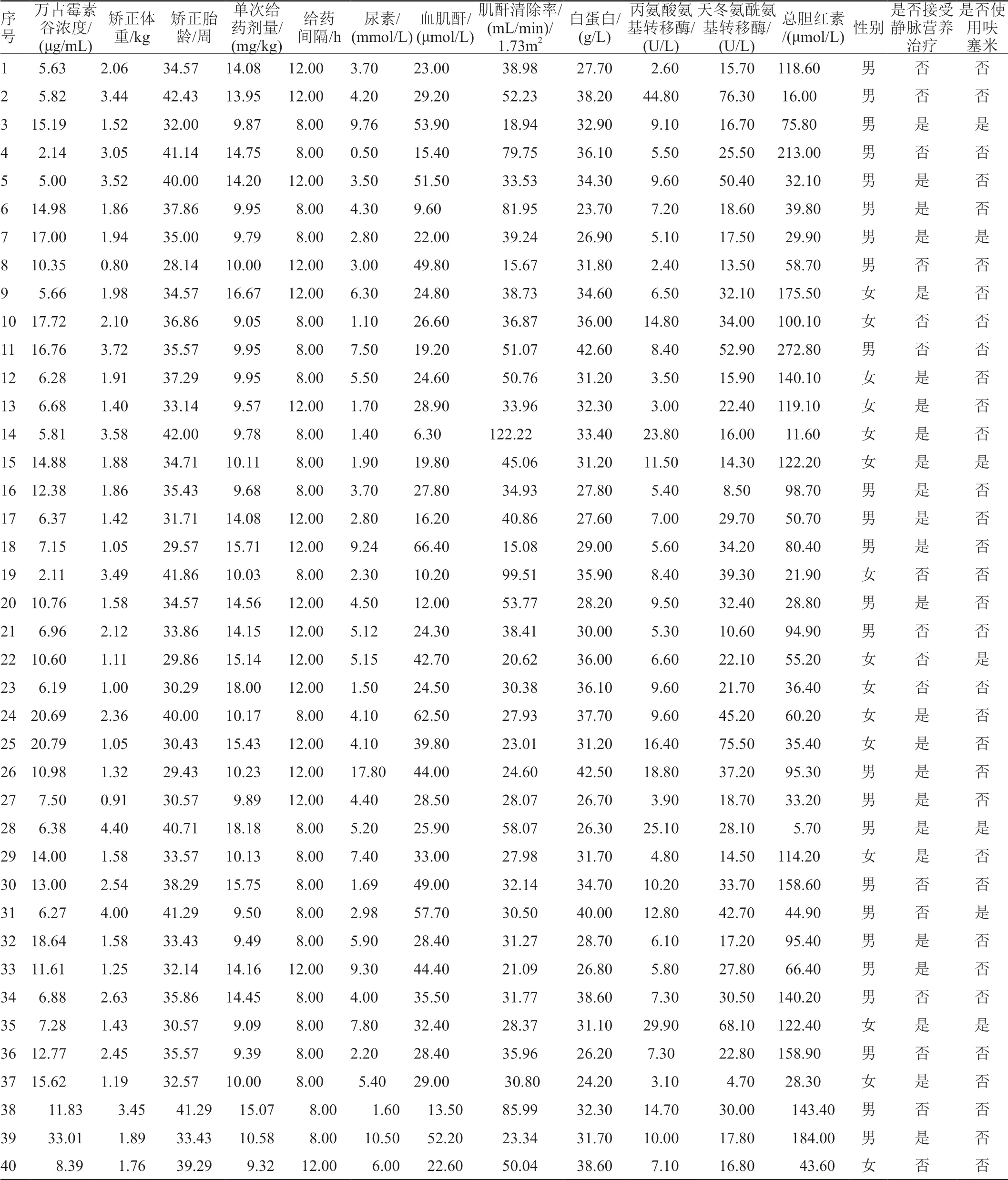
附表1患儿个体信息Appendix Tab.1 Baseline characteristics of individual patients
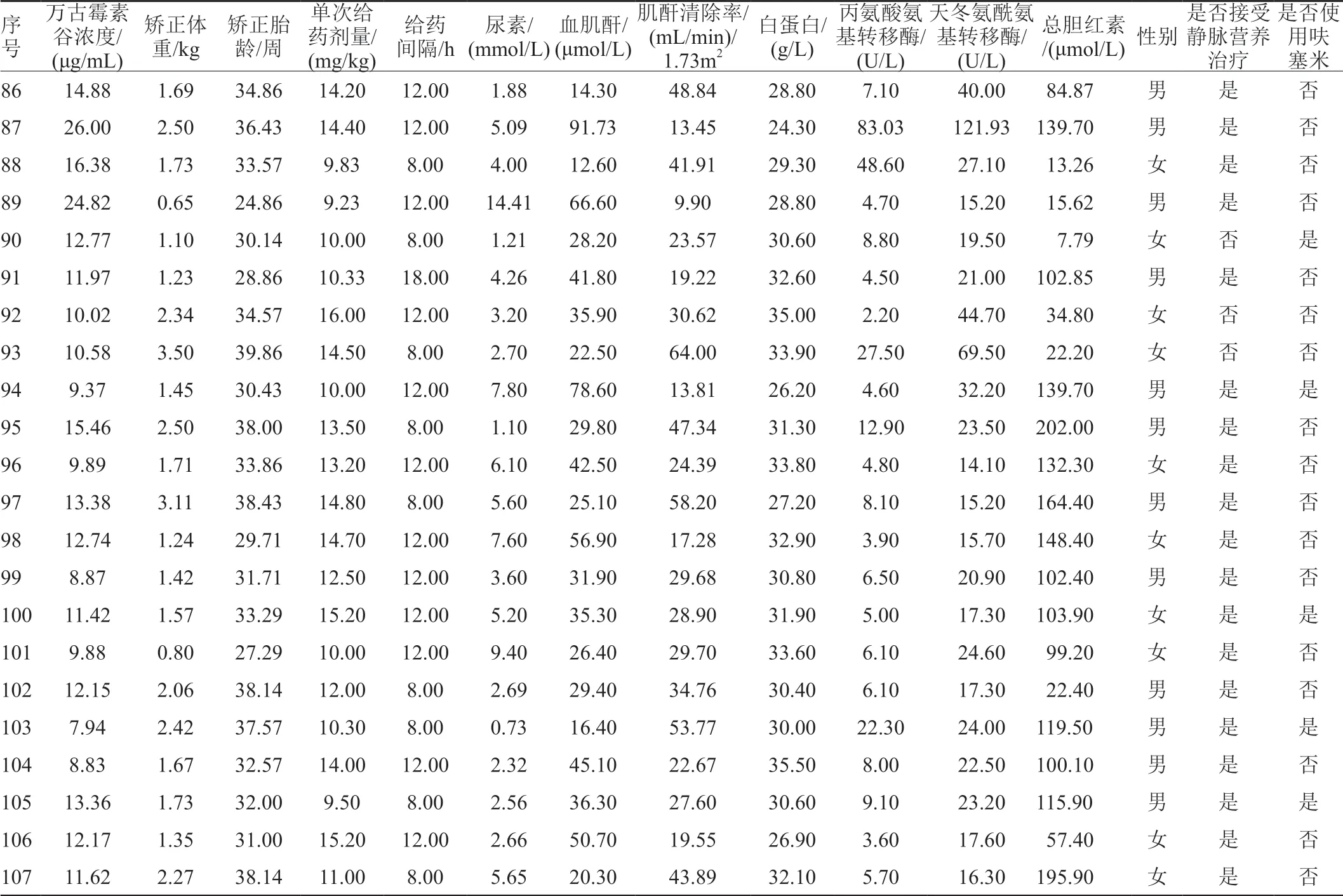
续附表1