一种基于改进密度峰值聚类的社区发现算法

黄炳森，陈羽中，2，3 ，郭 昆，2，3

1(福州大学 数学与计算机科学学院，福州 350116)2(福建省网络计算与智能信息处理重点实验室，福州 350116)3(空间数据挖掘与信息共享教育部重点实验室，福州 350116)

1 引 言

复杂网络中的社区发现是复杂网络研究的一个重要方向.生活中处处存在复杂网络，而如何划分出复杂网络中存在的社区结构在很多领域都是一个重要的问题.尤其是随着互联网的飞速发展，社交网络的涌现和大数据的发展，使通过社区发现算法分析网络的拓扑结构和层次结构成为社交网络研究的重要方向.社区发现研究有助于发现复杂网络中隐藏的规律，预测复杂网络的行为，帮助人们理解复杂网络的功能.

近年来，已有不少复杂网络社区发现算法被提出，根据算法的设计思想的不同，可以大致分为基于划分的方法、基于模块优化的方法、基于标签传播的方法、基于信息论的方法等.基于划分的社区发现算法主要是通过删除社区间的链接来实现社区划分，其中最具代表性的是Girvan和Newman 于2002提出的GN算法[1]，开启了社区发现算法的先河.Newman等[2]在2004年提出了模块度的概念，可以用来衡量社区划分的质量，随后以函数Q为目标函数的优化方法也成为复杂网络社区发现领域的主流方法之一.标签传播算法(LPA) 是一种基于图的半监督学习方法，其基本思路是用已标记节点的标签信息去预测未标记节点的标签信息，2007年，Raghavan等[3]首次将LPA算法应用于社区发现，后来衍生出了许多基于标签传播的社区发现算法，如SLPA[4]，CRD-LPA[5]，LPA_LRDC[6]等.从信息论的角度出发，Rosvall等[7]把网络的模块化描述看作对网络拓扑结构的一种有损压缩，从而将社团发现问题转换为信息论中的一个基础问题.

从图论的角度，可以将社区发现看作图上的聚类过程.因此，不少基于聚类思想的算法也被应用到社区发现中.Rodriguez等[8]于2014年提出了密度峰值聚类算法，此聚类方法不像一般的聚类算法有比较高的参数敏感性，只依赖于节点间的距离，该方法能够获得较稳定的聚类结果.黄岚等[9]通过相似度定义网络中各节点之间的距离，将密度峰值聚类算法应用于社区发现中.金志刚等[10]提出了一种基于密度峰值聚类的自适应社区发现算法，能够减少社区发现算法中参数的选择对社区划分的影响.隋鹏等[11]提出了用户亲密度的概念来衡量两个节点的距离，将社区发现与密度峰值聚类相结合，但是引入过多的参数.冯国香等[12]引入了概率分布矩阵将密度峰值聚类应用在重叠社区.虽然以上几种算法都将密度峰值聚类应用到社区发现，但是在选取簇中心的环节上仍然需要人工选取而没有提出自动选取的策略，算法的性能有一定缺陷且存在主观因素.

本文提出了一种基于等效电阻距离和自动选取密度峰值簇中心的社区发现算法CDRDCS(Community Discovery based on equivalent Resistance Distance and automatic density peak cluster Center Selection)，将改进后的密度峰值聚类算法应用到社区发现，并实现密度峰值簇中心选取的自动化.

2 基于改进密度峰值聚类的社区发现算法

2.1 密度峰值聚类

密度峰值聚类(Density Peak Clustering，简称为DPC)算法的核心思想在于簇中心的刻画，一个节点能成为簇中心，需要具备具如下两个重要性质：

1)本身的密度大，即它被密度均不超过它的节点包围；

2)与其它密度更大的节点之间有相对较大的距离.

对于任意一个节点i，需要求其局部密度和相对距离两个属性.这两个变量值的计算只取决于图G中任意两个节点vi，vj之间的距离，两个属性定义如下所示：

定义1.局部密度ρ：

(1)

其中dc为截断距离，dij为vi与vj的距离.不难看出节点i在dc领域内的包含的节点数越多，局部密度ρ就越大.

定义2.相对距离δ：

(2)

公式(2)表示：当节点i具有最大局部密度时，δi表示与i距离最大的节点与i之间的距离；否则，δi表示在所有局部密度大于i的节点中，与i距离最小的节点与i之间的距离.求得图G中每个节点的ρ和δ后，在二维坐标图上以ρ为横坐标，δ为纵坐标，可以画出用来确定簇中心的决策图.通过观察决策图，选取具有相对较大ρ和δ的节点为簇中心.簇中心确定后，按照局部密度ρ从大到小的顺序将每个节点跟随到距离最近的簇中，生成最终的簇.

2.2 CDRDCS算法

2.2.1 算法设计思想

复杂网络可用图结构G=(V，E)来表示.算法CDRDCS算法输入的是一个网络图G，经过处理后划分出k个社区集合C={Ci|i=1，2，3，…，k}.

CDRDCS算法的核心步骤如下：

1)引入基于等效电阻理论的距离度量方式，计算G中任意两节点距离.

2)在生成的节点距离基础上，运行DPC算法，并生成决策图.

3)采用DBSCAN在决策图上自动确定簇中心.

2.2.2 基于等效电阻理论的节点距离计算

首先，根据2.1节的介绍，DPC算法需要求两个重要属性ρ和δ，而ρ和δ的取值需要根据节点间的距离来计算.因此，对于给定的图G，引入一种基于等效电阻理论的计算方式来衡量两个节点间的距离[13].

在图G中任意两点vi和vj之间的路径有两种情况：

1)vi和vj之间只有一条路径.

2)vi和vj之间存在多条路径.

对于第一种情况vi和vj之间的距离即两点间的路径长度.对于第二种情况，设节点vi和vj中m条路径的长度分别为P1，P2， …，Pm，如图1(a)所示.将节点vi和vj看成并联电路中的两个电势Ui和Uj，这m条路径看成为电路中的m条分支，而每条分支的电阻可看成每条路径长度通过映射函数映射的值，如图1(b)所示，进而可求出电势Ui和Uj之间并联电路的等效电阻RE，从而通过反向映射计算出vi和vj之间的等效路径长度PE.

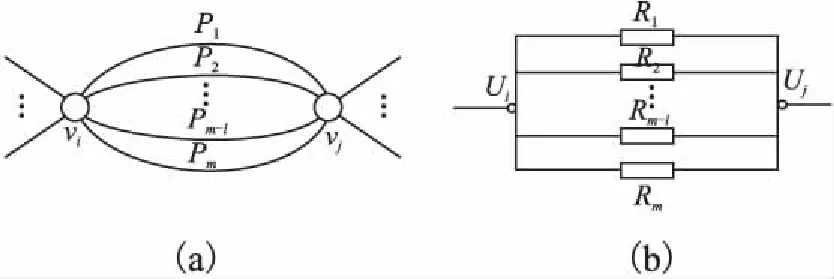
图1 两点间路径的电路表示Fig.1 Circuit representation of a path between two points

令路径长度与电阻的映射函数为Rn=f(Pn)，其中f的定义如公式(3)所示.

f(P)=eP-1

(3)

根据并联电路等效电阻的理论，由公式(4)可以求得等效电阻RE

(4)

联立公式(3)和(4)可以得到公式(5)

(5)

其中PE为vi与vj间的等效路径长度.

则节点vi与节点vj之间的等效电阻距离Dij的计算方式如公式(6)所示

(6)

计算任意两个节点间的所有路径的长度是一个NP难问题.在复杂网络中，由于具有小世界特性，节点间路径越长，带来的信息量就越小.因此，将距离大于2的路径看作电路断路处理，在计算两点间的等效路径时只取其中小于等于2的路径来参与计算，舍去大于2的路径，当两点间所有路径都大于2时，则认为这两点间的距离为无穷远.同时，这样处理后将不会出现路径并联和串联交替的现象，使得在求等效路径时的计算方式极大简化.

根据并联电路等效电阻理论得到的节点间的等效距离能够有效地用来衡量复杂网络中的节点距离，在网络结构中相比于其它距离的计算方式，此种距离度量方式考虑了两点间的所有路径，将所有路径考虑进来计算等效距离，两点间的路径越长，距离就越大，路径越多距离就越短，能使处于同一个社区的节点联系更加紧密，能更好地表示节点间的远近.相比于最短路径只考虑单一的一条路径，在社区发现中往往需要考虑到两点间多方面的联系.

2.2.3 基于DBSCAN的自动簇中心选择

DPC算法中，在决策图上选取簇中心时，需要人工看图来判断哪些点是簇中心.这将带来很大的不便并且存在主观因素，某些情况下不同人选取的簇中心可能会各不相同.为了解决这个问题，提出一种利用DBSCAN算法[14]来自动筛选簇中心的方法.

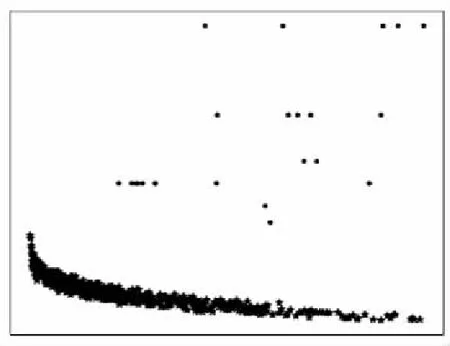
图2 DBSCAN确定簇中心Fig.2 DBSCAN determine the cluster center

通过观察图2，不难发现决策图中非簇中心的点聚集在一起，分布在决策图的左下方.而簇中心则零散地分布在右上方.针对这个特性，我们将决策图上的点看成二维平面上的散点图，应用DBSCAN算法对决策图上的点进行聚类，其中非簇中心将被聚集到同一个最大的簇中，最大簇外的其它点即为簇中心，如图2所示.

2.2.4 算法实现

为了将DPC算法应用于社区发现，在距离的度量上采用2.1节提到的基于等效电阻理论计算得到的等效距离.实验也表明了该距离度量和密度峰值相结合具有较好效果.在DPC决策图簇中心的选择上，采用2.3节提出的通过DBSCAN对决策图上的点进行聚类来自动获取簇中心.

CDRDCS算法的具体实现步骤如下：

输入：网络图G(V，E).

输出：社区划分C={C1，C2，C3，…，Ck}.

Step1.初始化节点的邻接关系.

Step2.根据2.1节的等效电阻距离计算方式计算任意两个节点间的等效距离dij.

Step3.将求得的所有节点间的距离dij输入到DPC算法，确定阈值dc.根据2.3节的公式计算每个节点的局部密度和相对距离.

Step4.将每个节点的ρ和δ进行归一化处理，以二维坐标集{(ρ，δ)}的形式输入到DBSCAN算法中，通过DBSCAN对决策图进行聚类，筛去属于最大簇的点集，从而求得簇中心节点.

Step5.根据DBSCAN得到的簇中心，按照从大到小的顺序对每个节点进行聚类，将节点划分的距离最近的簇中.

Step6.将聚类结果处理成社区划分的结果.

2.2.5 算法复杂度分析

首先分析算法的时间复杂度.设图G的节点数为v，边数为e.步骤1中，初始化节点邻接关系时间复杂度为O(v+e)；步骤2中，计算等效距离dij时间复杂度为O(e2/v)；步骤3中，确定dc的时间复杂度为O(vlogv)，计算ρ和δ的时间复杂度都为O(v2)；步骤4中，DBSCAN最坏情况下时间复杂度为O(v2)；步骤5中，对剩余点进行聚类的时间复杂度为O(v2).因此CDRDCS算法总的时间复杂度为O(4v2+e+e2/v+v+vlogv)=O(v2).

在空间复杂度方面，存储图G的邻接表需要O(v+e)的空间复杂度；存储节点间的距离矩阵需要O(v2)的空间复杂度；和都需要O(v)的空间复杂度；DBSCAN需要O(v)空间复杂度；存储划分的结果需要O(v)空间复杂度.因此CDRDCS算法总的空间复杂度为O(v2+5v+e)=O(v2).

3 实验结果与分析

3.1 实验数据

1)真实网络数据集

本文选用三个著名的真实网络来进行实验，分别为空手道俱乐部网络Karate，海豚网络Dolphin和橄榄球俱乐部网络Football，三个真实网络数据集的信息如表1所示.

Karate数据集中每个节点代表一个俱乐部成员，边表示两个成员交往密切.

Dolphin数据集中的每个节点代表一只海豚，边代表两只海豚有接触.

Football数据集中每个节点代表一支球队，边代表两只球队有比赛过，这些球队属于不同工会.

表1 真实网络数据集Table 1 Real network data sets

2)人工合成网络数据集

LFR人工合成基准网络[15]是测试社区发现算法性能的一种标准数据集.LFR基准网络具有无标度特征以及已知其社区划分结构两个优点.本文中一共采用6个混合因子mu递增的LFR基准网络N1～N6，具体参数如表2所示.在6个网络中，每个网络的节点数N=1000，网络中节点的平均度数k=20，节点的最大度数maxk=50，节点的度数分布参数t1和社区大小分布参数t2 分别为默认值2和1，最大社区规模maxc=100，最小社区规模minc=20，网络混合因子mu从0.1～0.6递增，混合因子越大网络中的社区结构越模糊，越不容易被发现.

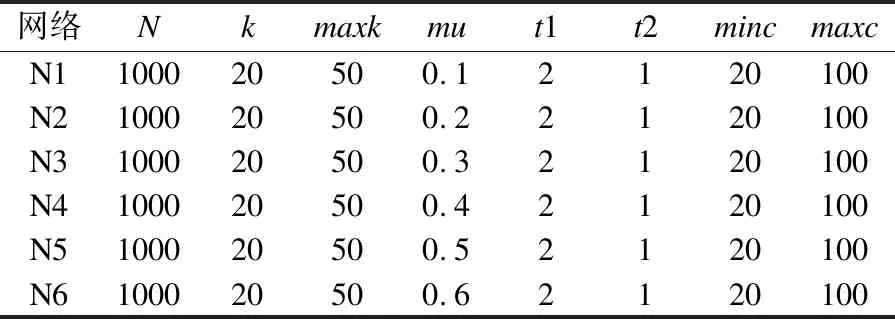
表2 人工合成网络数据集Table 2 Artificial synthesis of network data sets

3.2 评价指标

本文选用归一化互信息NMI[16]及模块度Q[1]为社区发现算法的评价标准.

1)NMI

NMI是由Lancichinetti等提出的用于测评已知网络结构划分结果的评价指标，定义为：

(7)

式中R为真实的划分结果；P为预测的划分结果；H(R|P)为R关于P的归一化条件熵.NMI值的范围为0～1，NMI值越高说明算法得到的划分结果与真实的划分结果越接近，NMI=1说明与真实划分完全一致.

2)模块度

模块度Q[1]由Girvan和Newman提出的用于评价社区结构稳定性的衡量指标，定义为：

(8)

式中m为网络总边数；A为网络的邻接矩阵，节点v与w相连接则Awv=1，否则为0；kv表示节点v的度数；当节点v与w处于同一社区时=1，否则为0.

3.3 实验结果分析

1)自动选取簇中心实验

图3 人工网络的决策图Fig.3 Decision graph of artificial networks

图3(a)～图3(f)所示为CDRDCS算法在6个mu值递增的LFR人工合成基准网络上得到的决策图.这里，采用的是DBSCAN算法自动选取簇中心，从图3(a)～图3(d)可以看出，当mu<0.5时决策图的簇中心比较明显，自动选取簇中心的方法能够较准确地找出所有的簇中心，与人工判别基本一致.当mu>0.5时，决策图中的簇中心逐渐模糊，算法识别效果变差.但是此时人工观察也很难判别出簇中心.

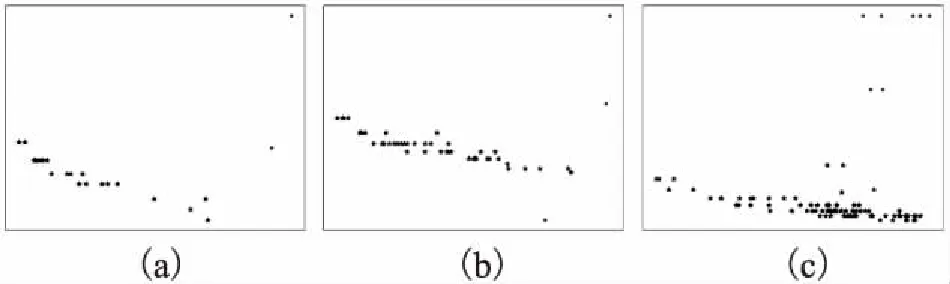
图4 真实网络的决策图Fig.4 Decision graph of real networks

图4(a)～图4(c)为CDRDCS算法在三个真实网络上得到的决策图.可以看出，真实网络的决策图中的簇中心虽然比较分散，CDRDCS算法仍可较准确地选出簇中心.

由于在一些情况下，某些δ值较低的点也会脱离决策图中的最大簇，但这些点并非簇中心，如图3(f)和图4(b)所示，对于这些异常点可通过设置一个较低的阈值δ′来过滤掉即可.

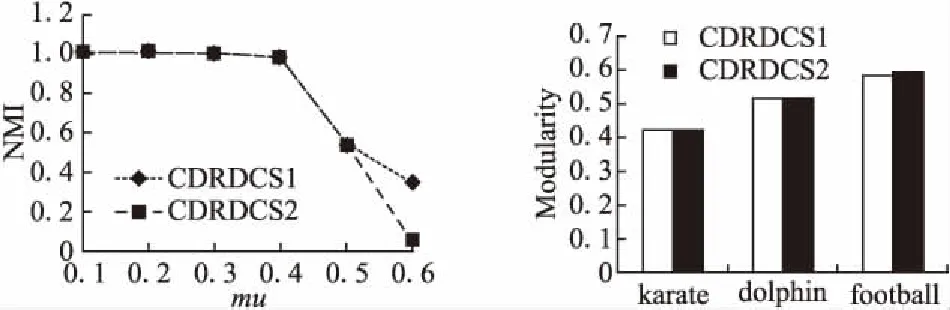
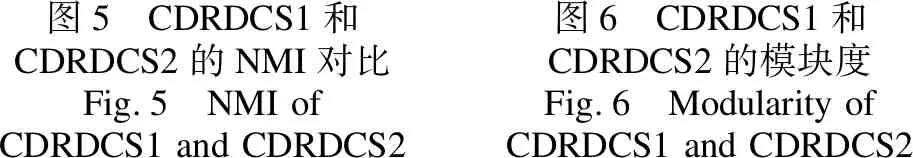
图5 CDRDCS1和CDRDCS2的NMI对比Fig.5 NMI of CDRDCS1 and CDRDCS2图6 CDRDCS1和CDRDCS2的模块度Fig.6 Modularity of CDRDCS1 and CDRDCS2

图5给出人工选择簇中心的方式(CDRDCS1)与自动选择簇中心方式(CDRDCS2)在6个mu递增的LFR人工合成基准网络上的NMI实验结果.图6为CDRDCS1与CDRDCS2在三个真实网络上的模块度实验结果.从两组实验看出，使用DBSCAN来自动选取簇中心与人工选择的效果基本一致，说明基于DBSCAN算法的自动选取簇中心方式能够达到与人工选择基本一致的效果.

2)与其它社区发现算法的精度对比实验

为了验证CDRDCS算法的有效性和可行性，在实验数据集上将CDRDCS与CPM[17]，SLPA[4]、LFM[18]和VDDPC[9]等四个社区发现算法进行实验，对比它们的社区发现精度.

从图7可以看出，几个不同算法在LFR人工合成基准网络mu增大的情况下都呈现出明显的下降趋.VDDPC、CPM、SLPA和LFM算法下降的趋势比较明显.而CDRDCS算法在mu小于0.4时仍然能保持较高NMI，从0.4后也开始明显下降.当mu达到0.6时，所有算法均难以区分社区结构.CPM算法是基于派系理论的，适用于完全子图较多的网络图，完全子图较少的情况下效果较差.SLPA算法是基于标签传播思想的，标签传播具有一定的随机性.LFM算法在初始化社区时具有随机性，划分结构不够稳定.CDRDCS算法由于是基于密度峰值设计的，受图结构影响较小，且选择了一种与DPC契合度较好的距离度量方式，所以在mu不是太高的网络结构下能有比较好的效果.

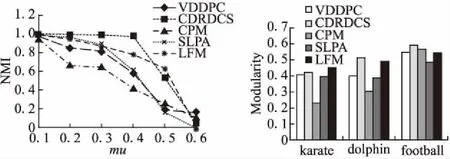
图7 不同mu人工网络中的NMIFig.7 NMI with different mu on artificial networks图8 真实网络中的模块度Fig.8 Modularity on real networks

从图8可以看出，除了在karate数据集上，LFM算法略高于CDRDCS算法外，在其它数据集上，CDRDCS算法的精度均高于对比算法.这主要是由于在CDRDCS算法中采用的基于密度峰值的聚类方法在选择簇中心时对节点的聚类过程与社区发现中检测社区中心并根据社区中心扩展社区的过程十分相似.因此，通过这种方式识别出的社区结构能具有较高的稳定性.

4 结束语

本文提出了一种基于改进密度峰值聚类的社区发现算法CDRDCS.首先，引入了一种基于等效电阻理论的距离度量方式来衡量网络节点间的距离.其次，在密度峰值聚类算法的簇中心选取过程中，提出采用DBSCAN算法来对决策图进行聚类自动选取簇中心，以取代人工选取，实现簇中心选择的自动化.在真实网络和人工网络上的实验表明，本文所采用的距离度量方式与密度峰值聚类算法相结合能够有效提高社区发现的精度.接下来，将进一步在更多自动发现簇中心方法探索与降低算法复杂度以适应大规模复杂网络等方面展开更深入的研究.