基于模糊综合评判的测控网运行评估仿真与实现

高惠荔，刘 彬，李文舒，徐 建，陈思远

(1.中国人民解放军63769部队，陕西 西安 710043；2.中国人民解放军63789部队，陕西 西安 710043)

0 引言

随着我国航天事业的飞速发展，太空运行的航天器迅速增多。不同种类、不同用途的卫星发射升空，地面测控站也相应地建设起来，地面测控网已形成具有一定规模的实用网络。为了有效地管理测控资源，合理使用测控设备，地面测控网运行管理需求越来越迫切。

在以往的测控网运行质量管理中，对测控网运行质量的评估仅停留在对卫星长期管理、任务跟踪任务成功率的统计和测控任务需求是否满足上，评价标准过于简单，缺乏对测控网运行质量的科学全面评估，不能从全网的角度反映测控网的整体运行情况，也无法对后续测控设备、测控网的发展和建设提供合理化建议。在轨航天器和测控设备的数目激增，技术复杂程度不断提升，粗放式的管理模式已经阻碍了航天测控网运行整体效能的提升。目前，在测控网运行质量评估方面，还没有比较完善的方法及规范，现代信息技术也没有在测控网的运行管理中得到高效应用。

评估理论起源于管理科学领域，从决策理论中提取、吸收而来，也融合了其他学科的理论并逐步发展。近20年来，管理科学、应用数学、系统论、信息论、计算机技术和人工智能技术等被引入系统评估领域，产生了一系列新的评估方法，如：模糊评估方法、灰度评估方法和人工智能方法等，评估方法的应用领域也日益广泛，已渗透至互联网系统、教育系统、农业系统和科技系统等，进行了网络质量、教学质量、粮食产量及项目的评估，带来了巨大的社会和经济效益[1-3]。

本文对测控网内同类设备运行质量评估开展了深入研究，该类评估系统具有多层次、多因素和主观性较强等特点，通过多种评估方法比较分析，最终采用模糊综合评判法进行处理分析，有效分析出测控网内设备运行质量和效益，为后续设备工作合理分配和提高测控网运行质量奠定了扎实基础。

1 测控网运行质量评估体系设计

1.1 测控网运行质量评估系统的组成

本文对测控网运行质量评估实际落脚点是针对网内各测控设备的运行质量而言的，该评估系统主要由7部分组成：评估目的、评估主体、评估对象、评估指标、权重、评估方法和评估结果[4-9]。

评估目的：对测控网管理范围内测控设备一段时间内的运行质量进行公平公正评估，促使形成有效良好的测控网管理运行评价机制，起到一定的激励作用；并通过评估数据自动采集的实现，进一步提升测控网管理的精细化和规范化水平，对测控网的合理运行提出有指导性的建议。

评估主体：主要面向测控网管理中心的管理者，也适用于设备总体单位或研制厂所对测控网运行质量关心的人员。

评估对象：考虑到当前测控网管理主要是地基设备，尤其以S频段设备为主，同时为了使评估结果不受不同设备性能的影响，本文研究的评估对象以基本上同时投入使用的一类设备为主，对其他类型测控设备评估时，可参考本文的研究方法执行。

评估指标：根据本文对测控设备运行质量的评估目的，确定该评估系统所需的评估指标。

权重：反映评估指标之间的相对重要性，是指标对总目标的贡献程度。当评估对象及评估指标都确定时，评估的结果就依赖于权重，即权重确定的合理与否，关系到评估结果的可信程度[10-12]。

评估方法：是在评估理论指导下进行具体评估采取的途径、步骤和手段等，评估方法一般分为定性方法、定量方法和定性定量相结合3类。

评估结果：通过一系列评估步骤后，得到评估结果，即评估方法产生的结论。评估结果只适应于性质相同的对象之间的比较和排序，具有相对意义，故要公正对待评估结果。

1.2 测控网运行质量评估指标体系的设计

为了将多层次、多因素和复杂的评估问题用科学的计量方法进行量化处理，针对评估对象构造了一个科学的评估指标体系，如图1所示。

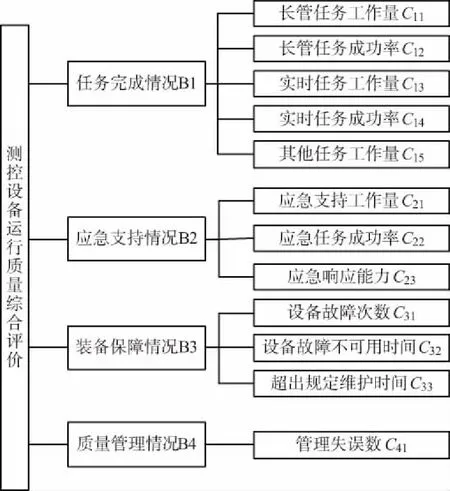
图1 测控网运行质量评估指标体系

2 基于模糊综合评判法的评估体系建模

运用模糊综合评判法建立相应数学模型，需要以下步骤：确定评价因素集、确定评价等级集、进行单因素评价、建立评价矩阵、确定权向量、进行模糊合成和做出决策[13-16]。

2.1 确定评价因素集

针对图1给出的准则层指标，这是一个典型的2层评价问题，相应的评价因素划分为2个层次，其中，U1={c11，c12，c13，c14，c15}，U2={c21，c22，c23}，U3={c31，c32，c33}，U4={c41}为第1层次，U={B1，B2，B3，B4}为第2层次。

2.2 确定评价等级集

将评价等级划分为4个等级，即V=(优秀、良好、一般、差)。对于评价因素集中的每个因素ui(i=1，2，…，4)，vj(j=1，2，…，4)分析其对于评价等级集的隶属度rij，得出第i个因素的单因素评价结果：ri=(ri1，ri2，…，ri4)。

2.3 多专家进行单因素评价

针对第1层次的评价因素，分别由多名专家对每套设备进行测评，并将专家测评结果进行累加，进行归一化处理，得到各评价因素隶属于评价等级集中各等级的测度值，即得到第1层次的模糊评价矩阵R1，R2，R3，R4。

对于m个因素，进行单因素评价后，将ri作为第i行，形成一个综合了m个因素n个评价等级的模糊矩阵R。

2.4 确定权重

求权重是综合评价的关键。层次分析法是一种行之有效的确定权系数的有效方法。层次分析法的步骤大致如下：

① 确定目标和评价因素

P个评价指标，u={u1，u2，…，up}。

② 构造判断矩阵

判断矩阵元素的值反映了人们对各元素相对重要性的认识，一般采用1～9及其倒数的标度方法。但当相互比较因素的重要性能够用具有实际意义的比值说明时，判断矩阵相应元素的值则取这个比值，即得到判断矩阵：

S=(uij)p×p。

③ 计算判断矩阵得出权重

计算判断矩阵的最大特征根λmax，及其对应的特征向量A，此特征向量就是各评价因素的重要性排序，也是权系数的分配。

利用层次分析法，分别得到一级指标和二级指标的权重。与第1、2层评价因素对应，权重矢量分别为：W1={wc11，wc12，wc13，wc14，wc15}，W2={wc21，wc22，wc23}，W3={wc31，wc32，wc33}，W4={wc41}，W={wb1，wb2，wb3，wb4}对于权重wi，要求wi≥0且∑wi=1。

2.5 进行模糊合成

在模糊矩阵R和权重向量W已经确定的基础上，对二级指标进行模糊合成。用模糊算子表示为：

Si=Wi*Ri。

常用的模糊算子符号有Zadeh算子、加权平均算子、环和乘积算子、有界算子、取大乘积算子、有界和取小算子、有界和乘积算子、Einstein算子、Hamacher算子和Yager算子等。本文选用加权平均算子(●，+)，进行加权平均运算。

S1=W1*R1，S2=W2*R2，

S3=W3*R3，S4=W4*R4。

然后，对计算得到的S1～S4，组合形成对一级指标的模糊综合评价矩阵R：

R=[S1，S2，S3，S4]。

最后，将权重向量W与模糊综合评价矩阵R合成模糊综合评价结果向量S：

S=W*R。

选定了模糊算子进行S的计算后，需要对S进行归一化，使∑sj=1。

2.6 做出决策

根据模糊综合评价结果向量S，可以按照最大隶属度法则，或者赋予不同的等级一个权重向量W′，从而使每个被评价对象综合得到一个评价值，做出决策。

最大隶属度法则：针对评价结果向量S=(s1，s2，s3，s4)，sj表示被评价对象隶属于评价等级vj的程度。其中，s中最大的sj对应的等级vj表示被评价对象最适合于该等级，可以用该等级作为被评价对象的评价结果。

该方法简单便于理解，但由于该方法只选取S中的最大值对应的等级，而其他非最大值对应的信息被忽略，使得评价结果损失的信息较多，不能全面反映评价对象的情况，只能对评价对象做大致评判。

加权平均法则：针对4个评价等级优秀、良好、一般和差，设置等级权重向量W′={4，3，2，1}，将各个评价对象的结果向量S=(s1，s2，s3，s4)分别与W′中各等级对应的权值进行加权求和，得到各个评价对象的综合评分值，最后根据分数值的大小进行排序。

这样，综合评价结果向量S解模糊后的结果可直接得到全部评价对象的从高到低的排名。该方法全面考虑并利用了评价结果向量S中的信息，较全面客观地对评价对象做出评价，根据本项目的研究需要，拟采用加权平均法则做出决策。

3 数值计算及仿真验证

3.1 数值计算

本文分别单独计算B1～B4项的得分后，利用B1～B4项的分值再次模糊加权计算得到最终得分并进行排名显示，由于B1～B4项和总的计算采用的软件编程方法相同，这里以B1项为例对程序进行说明。表1～表3为设备跟踪历史试验数据，其中，表3中PT表示平均值。

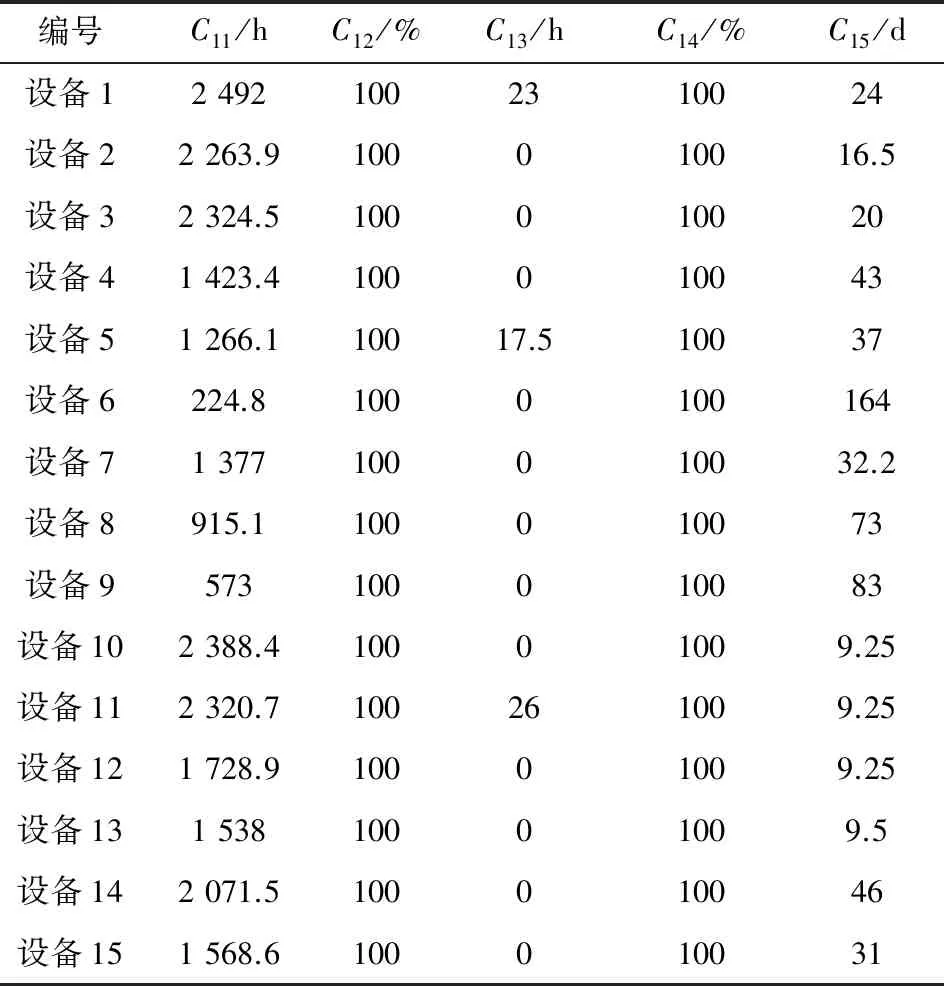
表1 15套设备(c11～c15)数据

表2 专家对(c11～c15)的权重分配

表3 专家对(c11～c15)数据的评价标准(选取部分)

隶属度法则，或者赋予不同的等级一个权重向量W′，从而使每个被评价对象综合得到一个评价值，做出决策。

3.1.1 计算判断矩阵

采用的是层次分析法确定不同评价因素的权重。根据给定的评估数据中5位专家对B1中各小项(c11～c15)所占的权重比例及重要程度分配，进行求平均，进而得到判断矩阵。

① 求c11～c15平均

c11的平均=(专家1c11+专家2c11+专家3c11+

专家4c11+专家5c11)/5=9.24；

c12的平均=(专家1c12+专家2c12+专家3c12+

专家4c12+专家5c12)/5=9.08；

c13的平均=(专家1c13+专家2c13+专家3c13+

专家4c13+专家5c13)/5=9.16；

c14的平均=(专家1c14+专家2c14+专家3c14+

专家4c14+专家5c14)/5=9.76；

c15的平均=(专家1c15+专家2c15+专家3c15+

专家4c15+专家5c15)/5=8.92。

② 求判断矩阵

3.1.2 计算权重

计算步骤如下：

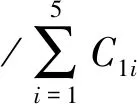
计算得到B1=(0.200 2，0.196 7，0.198 4，0.211 4，0.193 2)。

3.1.3 评价矩阵与等级权重模糊合成与排序

B1项的运行结果截屏如图2所示。

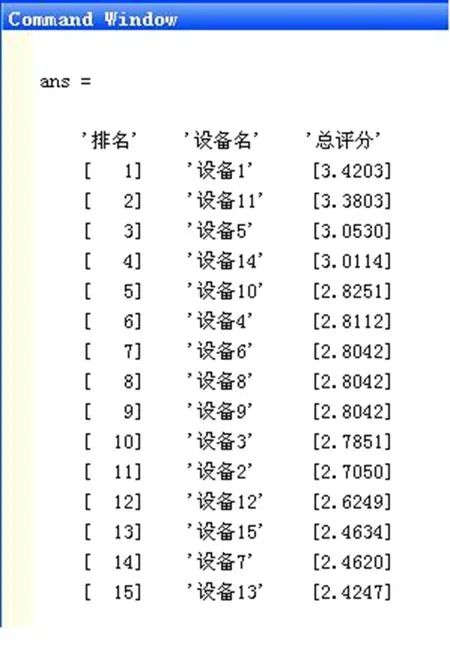
图2 B1项的运行结果

3.2 仿真验证

针对本文的数学模型计算方式，经比较最终选择Matlab软件进行编译。

仿真模型选取了参加日常测控工作的15套在用测控设备，评估周期为2015年1月1日至2015年6月30日，评估数据来源来源于设备跟踪卫星历史试验数据。B1部分程序截屏如图3所示。最终评估结果截屏如图4所示。

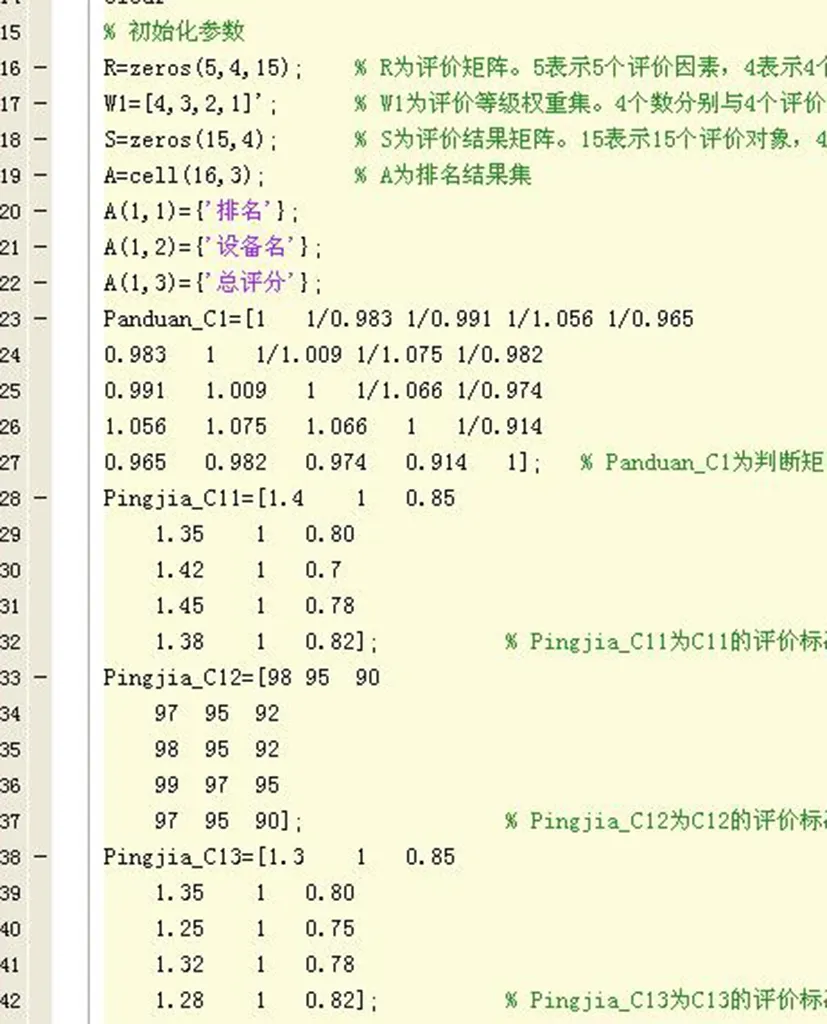
图3 部分程序截图

图4 评估结果

仿真结果得出了15套在用设备在测控网运行半年以来的综合评价得分，充分反应出15套设备对测控网的贡献率和使用率，该结果与半年以来的历史数据相吻合，仿真结果可信。

4 结束语

通过对选取的测控网内15套典型设备建立仿真模型，并运用本文构建的运行评价体系和模糊综合评判方法，以半年内测控网运行期间的设备跟踪数据作为输入，仿真计算得出的设备在测控网内运行质量情况与实际运行结果一致。因此，本文所构建的测控网质量运行评估体系科学合理，能够较为全面、快速和准确地反映出测控网内设备运行状态和测控网运行质量，能为后续科学合理调配测控网内设备资源作为依据，更好地提供全网的运行质量和效益。