有向复杂网络结构熵的软件动态执行关键节点挖掘算法

王 倩,胡松旺,郭嘉伟,任家东,赵小林

1(燕山大学 信息科学与工程学院,河北 秦皇岛 066000)2(河北省软件工程重点实验室,河北 秦皇岛 066000)3(北京理工大学 软件安全工程技术北京市重点实验室,北京 100081)

1 引 言

软件高性能和高效率需求的不断提升,使得软件网络越来越复杂,软件发生故障的可能性也随之增大[1].在软件开发过程中,模块存在缺陷是不可避免的,运用有限资源对软件系统进行彻底测试几乎是不可能的[2].而这部分模块对软件的质量及可维护性都会造成影响,是故障产生的直接原因[3].事实上,软件本身具有“类不平衡”的特点,即有缺陷的软件模块数量远少于无缺陷的软件模块数量[4].Fenton 等人[5]研究发现,如果在软件发布前的测试阶段,发现少数模块中存在缺陷,那么,在软件动态执行状态下,绝大多数缺陷都与那些少数模块中的缺陷相同.李鹏等人也指出缺陷之间并非独立存在,而存在相互关联[6].因此,如果能够从软件的体系结构出发,探究缺陷的产生和传播机制,找到软件中缺陷倾向性较大的模块,即软件网络中的关键节点,对于缩小测试范围、降低测试成本、提高软件质量具有重要的参考价值.

实践表明,软件架构的决策对软件系统的开发及软件质量有着重要的影响[7].为了最大程度提高软件质量,需要对软件系统潜在缺陷进行准确的预测.早期的主要预测方法主要包括各种统计技术和机器学习技术[8],如判别分析、逻辑回归、因子分析、模糊分类、贝叶斯网络、神经网络等.随着缺陷预测技术的不断成熟,单纯预测缺陷是否可能存在已经不足以满足缺陷分析的要求,开发人员更加关注缺陷在软件网络节点间的关联性,以获取更有效的缺陷预测途径.

软件模块缺陷的倾向性与模块所处位置及其组成结构相关[9].Valerde等人[10]将软件的相关信息映射到无向图结构,通过分析源代码,以类为节点、类间关系为边,构建了软件网络并证明了该网络模型的小世界和无标度等复杂网络结构特性.在此基础上,Myers等人[11]用有向网络结构进一步解决无向网络不能确切表示诸如类的继承、调用等关系的问题,表示了软件中函数之间的协作关系.受到复杂网络研究成果的影响,很多学者将其应用到对软件网络的研究,根据软件网络的拓扑结构特性定量描述节点的重要程度成为研究的热点.复杂网络中典型的中心性算法[12]有度中心性、介数中心性、局部中心性等,Pan等人[13]采用k核分解方法计算节点的中心性来衡量节点的重要程度,汪北阳等人[14]证明了缺陷传播能力在节点入度和出度较大的时候表现明显,通过实验分析软件网络的统计特性与影响力节点间的关系.胡思文等人[15]结合节点的邻居节点度和边权重构建不同的h指数用以度量软件网络中的类的重要性,上述三种方法都是在类的粒度上进行.Bhattacharya等人[16]采用函数和模块两种粒度级别的图结构,通过自定义的节点排名值将节点按重要程度排序,从而发现软件缺陷部位,该方法具有更细的粒度级别,但上述方法都只考虑了节点在网络中的局部属性.黄国言等人[17]根据函数调用关系计算从叶子节点到某节点的缺陷累计概率,是全局性的度量,但概率的赋值不够客观.

结构熵作为系统的有序性度量方法可以有效地从整体角度客观地分析网络中节点的组成情况,进而反映节点的重要程度.Tutzauer[18]等人提出了一种基于熵的中心性度量方法,当网络中存在环路时,该方法的性能很差.曹淑娟等人[19]在复杂软件网络特征学习的基础上,基于图的独立集合和图的匹配提出了一种新的图熵度量方法,此方法需要对新指定的特殊图类的图熵进行学习,并且对极值的学习要求非常高.Turnu等人[20]定义了描述节点度分布的结构熵,发现了软件网络中结构熵的统计信息可以关联到软件的漏洞数量,证明软件网络的结构特性与软件质量的关系.受上述启发,本文选取函数粒度级别为研究对象构建软件有向复杂网络模型,引入结构熵的概念,提出一种有向复杂网络结构熵的软件动态执行关键节点挖掘算法(Structure Entropy of Directed Complex Network based Key node mining algorithm in Software dynamic execution,简称SDKS),从缺陷产生和传播两个角度定义函数节点的结构脆弱性和传播性,通过调用和被调用关系的方向性,定义向下结构熵和向上结构熵,分别将其平均结构熵作为关键节点的选取依据.

2 相关定义

DSCN(Software Directed Complex Network)为软件有向复杂网络.该网络可用一个二元组DSCN=(V,E) 来表示.其中,V表示软件的函数节点集合,E表示带函数调用关系集合.vi表示函数节点i,eij表示函数节点间的调用关系,即函数节点i调用函数节点j.

定义1.Wu结构熵[21].

(1)

其中,ki为节点i的度,n为网络的节点数.

基于Wu结构熵采用节点的相对度值度量复杂网络均匀程度的思想,本文根据软件复杂网络中的相关特性,对结构熵的定义进行扩展,定义节点的向下结构熵和向上结构熵.

定义2.函数节点向下的结构熵.

(2)

其中,ODi表示节点i的出度,OS(vi)表示被节点i直接指向的节点集合.节点的向下结构熵采用递归方法,由自身和所有出度方向直接或间接相关的节点的熵组成.

定义3.函数节点向上的结构熵.

(3)

其中,IDi表示节点i的入度,IS(vi)表示直接指向节点i的节点集合.节点的向上结构熵同样采用递归方法,由自身和所有入度方向直接或间接相关的节点的熵组成.

定义4.函数节点向下的平均结构熵.

(4)

定义5.函数节点向上的平均结构熵.

(5)

定义6.结构脆弱性.节点的结构脆弱性是指,如果被函数节点调用的其它函数节点存在缺陷,那么,这个节点可能因为结构的包含关系引入缺陷并受到影响.

定义7.结构传播性.节点的结构传播性是指,如果存在缺陷的节点被其它函数节点调用,它可能通过依赖关系的结构特点影响调用它的节点.

定义 8.关键节点.关键节点分为结构脆弱性关键节点和结构传播性关键节点,如果满足OH(i)≥OHaverage,那么,节点i是结构脆弱性关键节点;如果满足IH(i)≥IHaverage,那么,节点i是结构传播性关键节点.

3 本文提出的算法SDKS

本文根据软件动态执行调用关系,在函数粒度级别生成软件有向复杂网络,对于一个函数节点,从主动调用的角度,如果它调用了一个缺陷点,它会受到缺陷的影响;从被调用的角度,如果它是一个缺陷点,它会将缺陷传递给调用它的函数,这就形成了“缺陷累积”效应和“缺陷波及”效应,表现为函数节点的结构脆弱性和传播性,对应于函数节点的出度和入度.算法主要分为模型的构建和关键节点的挖掘两个阶段.

3.1 软件有向复杂网络的构建

研究复杂软件系统的实体故障性特征,首先要追踪软件的执行行为,得到软件实体之间的关联关系,将软件执行过程映射为序列模型和网络模型,主要包括数据的收集、精简函数跟踪数据和数据的可视化.

1)数据的收集.采用GNU编译工具和Pvtrace追踪工具获取软件动态执行路径,追踪结果记录被写入trace.txt文件.

2)精简函数跟踪数据.trace.txt文件中包含了一系列带前缀字符的地址信息.前缀E表示函数的入口,X表示函数的出口.通过Addr2line工具将指令的地址转换成函数名,精简后的结果记录被写入graph.dot文件.

3)数据的可视化.采用可视化工具如Graphviz,可将节点及节点之间的依赖关系以图形化的方式展示,其dot工具可以根据graph.dot生成图片文件.

图1描述的是简单软件函数粒度级别建模过程.

图1 简单软件函数关系调用的建模过程Fig.1 Modeling process of simple software function calls

图1中,函数地址和函数名称的对应关系如下:

0x8048690→M(main),0x804854d→B,0x8048585→C,x80485b8→D,0x80485f0→E,0x8048623→F,0x8048656→G.

3.2 关键节点的挖掘

本文根据软件动态执行节点间的调用和依赖关系,在软件有向复杂网络的函数粒度级别挖掘结构脆弱性关键节点和结构传播性关键节点.采用节点向下子网络和向上子网络的各节点在全网络中的度分布熵值的和来度量节点向下子网络和向上子网络的复杂程度,复杂度越大,说明网络的规模越大,那么,节点调用或依赖范围越大.节点向下结构熵及平均向下结构熵的算法描述如算法1.

算法1.getAllEntrp(matrix)

输入:软件有向复杂网络邻接矩阵matrix

输出:所有节点的向下结构熵值集合entrpList及向下结构熵的平均值

1:n=软件网络中节点数目;

2:fori=1 tondo

3:flag=zeros(1,n);

4:entrplist[i]=getNEntrp(matrix,i,flag);

5:meanEntrp=mean(entrplist); //计算平均向下结构熵

6:returnentrplist,meanEntrp;

节点的熵值由自身和关联节点熵值的和组成,算法1通过调用函数getNEntrp计算每个节点的熵值,函数getNEntrp通过调用函数getEntrp计算节点自身的熵值.

functiongetNEntrp(matrix,x,flag)

输入:软件有向复杂网络邻接矩阵matrix,节点序号x,访问标记flag

输出:节点的熵值Entrp

1:n= size(matrix); //n为节点数目

2:if sum(matrix[x,:])== 0 //如果节点x无子节点,x是叶节点且熵值为0

3:Entrp=0

4:else

5:flag[x]=true;

6:idx=所有x节点的子节点的序号组成的数组;

7:SubEntrpLoop=zeros(1,n); //该数组用来记录x的子节点的熵值

8: fori=1 to length(idx)do

9: if(flag[idx[i]]!=true)

10:SubEntrp=getNEntrp(matrix,idx[i],flag);

//递归算x的子节点的熵值

11:SubEntrpLoop[i]=SubEntrp;

12:Entrp= getEntrp(matrix,x)+sum(SubEntrpLoop);

//节点x的熵值为自身的熵值加上x的子节点的熵值

13:returnEntrp;

functiongetEntrp(matrix,x)

输入:matrix,x

输出:节点的自身熵值

1:p=节点x的出度/软件网络各节点出度的和;

2:if(p>0)

3:entropy=-p*log(p);

4:else

5:entropy=0;

6:returnentropy;

在计算节点向上结构熵及平均向上结构熵时,算法思想基本相同,本文的处理方法是将软件有向复杂网络邻接矩阵matrix进行行列转置,进而可以使用算法1进一步计算.

3.3 计算过程举例

图2中的有向复杂网络包含21个节点,以节点1和节点12为例,计算这两个节点的向下结构熵,度量两个节点的结构脆弱性程度.

节点1的出度为4,其向下子网络波及到的节点集合为{2,3,4,5,6,7,8,9,10,11},对应的出度分别为{2,0,0,1,0,3,0,0,0,0,0}.节点1的全局出度和为4+2+1+3=10.

图2 一个有向复杂网络Fig.2 A directed complex network

节点12的出度为4,其向下子网络波及到的节点集合为{11,13,14,15,16,17,18,19,20,21},对应的出度分别为{0,2,0,0,2,0,0,2,0,0}.节点12的全局出度和为4+2+2+2=10.

该网络的全部节点的出度和为20.

根据公式(2),计算过程如下:

OH(3)=OH(4)=0

OH(6)=0

OH(8)=OH(9)=OH(10)=0

OH(11)=0

最后,OH(1)=0.9865,同理,OH(12)=1.0127.

从这个例子中可以看出,叶子节点的出度为0,其对应的熵值也为0,表明叶子节点不能调用任何其它函数,因此,它不受任何其它函数的缺陷的影响.此外,算法的思想依赖于全局相对度,但算法能够进一步根据度分布情况区分全局度相同的节点的重要程度.节点1和节点12的直接邻居都是4个,叶子节点是6个,不同在于叶子节点的排布.当叶子节点有3个存在缺陷时,对于节点1来讲,如果出现在8,9,10号节点,那么,受影响的是7,进而影响到1号节点;对于节点12来讲,任意3个叶子节点存在缺陷,都会影响12号节点的2个直接邻居,导致12号节点受影响的程度变大.因此,12号节点相对于1号节点来讲,其结构脆弱性要大一些,与计算结果相符合.

4 实验及分析

实验在Intel(R)Core(TM)3.6GHz CPU和16G内存的台式电脑,在Windows 8系统下运行,编程环境为Matlab.实验采用开源软件Cflow和Tar的最新版本作为数据集,挖掘软件中熵值高于平均值的关键节点,并将本文提出的SDKS算法与经典中心性算法(度中心性DC,接近中心性CC,局部中心性LC).挖掘结果的前10名节点分别在SIR模型上作为传播源的传播结果进行比较,SIR模型是带有传播因子β的传播模型,该因子用于调节传播概率,本文主要研究节点之间的关联关系,假设存在缺陷则其传播概率为1,因此,设置β=1.Cflow1.4和Tar1.28的节点总数、平均熵值、关键节点数量如表1所示.

表1 Cflow-1.4和Tar-1.28的挖掘结果的相关参数
Table 1 Parameters of results on Cflow-1.4 and Tar-1.28

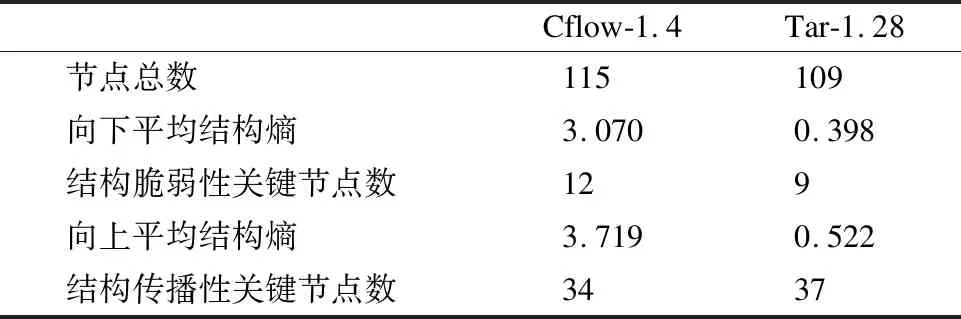
Cflow-1.4Tar-1.28节点总数115109向下平均结构熵3.0700.398结构脆弱性关键节点数129向上平均结构熵3.7190.522结构传播性关键节点数3437

由表1可以看出,结构脆弱性关键节点挖掘的数量相对较少,结构传播性关键节点的数量相对较多.这与实际软件开发是相符的.结构脆弱性体现的函数内部结构的复杂性,结构传播性则表示的是函数的复用性,在实际开发过程中,过于复杂的函数数量应该是有限的,而重用性高的底层函数会多一些.

表2～表5分别列出了本文算法与其它中心性算法的前10名节点的关键性在SIR模型上的验证结果,由每个节点所波及的节点数目来衡量,波及节点数越多,节点越关键.其中Name代表函数名,Num表示节点波及的函数个数.

表2 Cflow-1.4各算法前10名结构脆弱性关键节点在SIR模型波及的节点数
Table 2 Affected node number of top-10 structural vulnerability nodes in different algorithms in Cflow-1.4 on SIR model

SDKS算法DC算法CC算法LC算法函数名节点数函数名节点数函数名节点数函数名节点数main115tree_output31main115main115yparse76parse_variable_declaration71func_body71yyparse76parse_declaration71direct_tree12yyparse76parse_declaration71maybe_parm_list71main115tree_output31func_body71parse_function_declaration71fake_struct34parse_variable_declaration71parse_function_declaration71parse_typedef74declare16parse_declaration71parse_variable_declaration71dirdcl71func_body71maybe_parm_list71maybe_parm_list71dcl71yyparse76parse_dcl71tree_output31parse_dcl71yylex25dirdcl71parse_typedef74parse_knr_dcl71parse_typedef74parse_typedef74dirdcl71总计762总计525总计722总计722

从表2到表5的数据可以看出,无论是前10名结构脆弱性关键节点还是结构传播性关键节点,在Clow-1.4和Tar-1.28中,本文提出的算法SDKS波及到的节点总数明显多于其它中心性算法.这是因为,本文算法考虑了网络的全局性,即全局节点间的关联关系,而其它中心性算法是一种局部的度量,这种局部的优势在于,短期内可以迅速波及更多节点,但是随着调用和依赖深度的增加,其波及的节点数量就无法得到保证.此外,从单个节点排名的情况来看,本文提出的算法SDKS中,排名与波及到的节点的一致性整体上优于其它算法,这说明算法在单个节点排名和全部节点波及节点的总数上都更加准确.

表3 Cflow-1.4各算法前10名结构传播性关键节点在SIR模型波及的节点数
Table 3 Affected node number of top-10 structural propagation nodes in different algorithms in Cflow-1.4 on SIR model

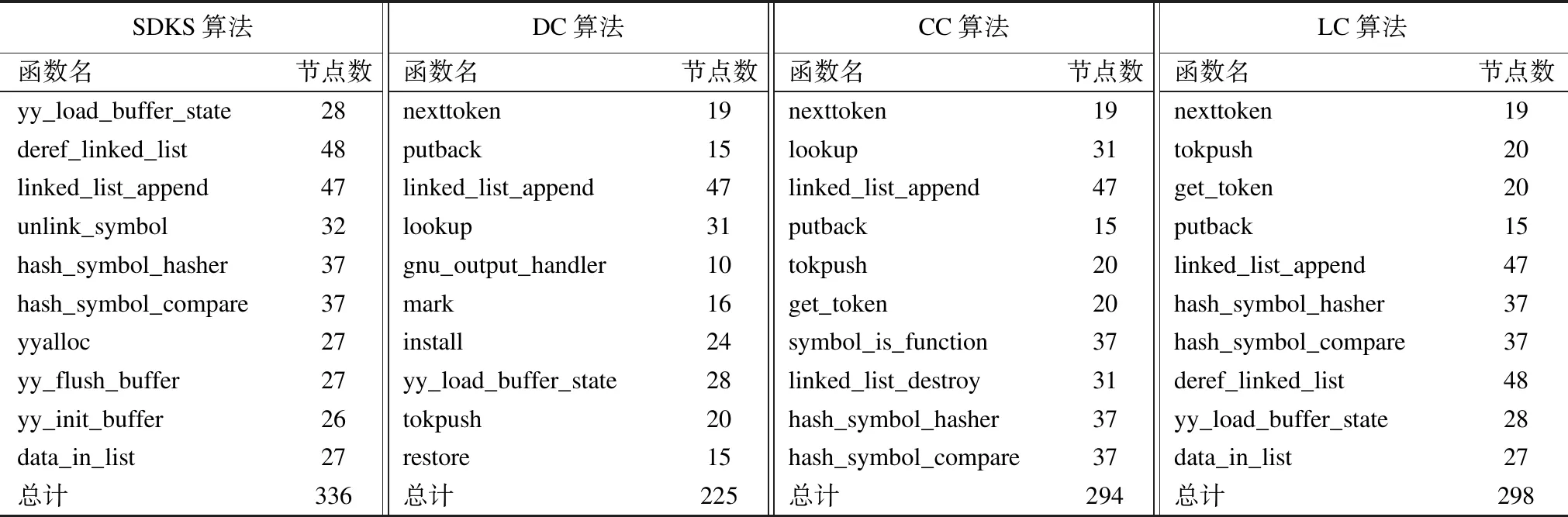
SDKS算法DC算法CC算法LC算法函数名节点数函数名节点数函数名节点数函数名节点数yy_load_buffer_state28nexttoken19nexttoken19nexttoken19deref_linked_list48putback15lookup31tokpush20linked_list_append47linked_list_append47linked_list_append47get_token20unlink_symbol32lookup31putback15putback15hash_symbol_hasher37gnu_output_handler10tokpush20linked_list_append47hash_symbol_compare37mark16get_token20hash_symbol_hasher37yyalloc27install24symbol_is_function37hash_symbol_compare37yy_flush_buffer27yy_load_buffer_state28linked_list_destroy31deref_linked_list48yy_init_buffer26tokpush20hash_symbol_hasher37yy_load_buffer_state28data_in_list27restore15hash_symbol_compare37data_in_list27总计336总计225总计294总计298

表4 Tar-1.28各算法前10名结构脆弱性关键节点在SIR模型波及的节点数
Table 4 Affected node number of top-10 structural vulnerability nodes in different algorithms in Tar-1.28 on SIR model

SDKS算法DC算法CC算法LC算法函数名节点数函数名节点数函数名节点数函数名节点数main109dump_file067create_archive93dump_file067create_archive93start_header23dump_file067create_archive93dump_file67create_archive93main109dump_file67dump_file067dump_regular_file36dump_dir067dump_dir067dump_dir67main109dump_file67main109dump_dir067dump_dir067dump_dir67dump_dir67dump_regular_file36dump_hard_link35dump_regular_file36dump_regular_file36dump_hard_link35_open_archive13dump_hard_link35dump_hard_link35start_header23close_archive15start_header23start_header23close_archive15decode_options8_open_archive13open_archive15总计579总计466总计577总计579

表5 Tar-1.28各算法前10名结构传播性关键节点在SIR模型波及的节点数
Table 5 Affected node number of top-10 structural propagation nodes in different algorithms in Tar-1.28 on SIR model

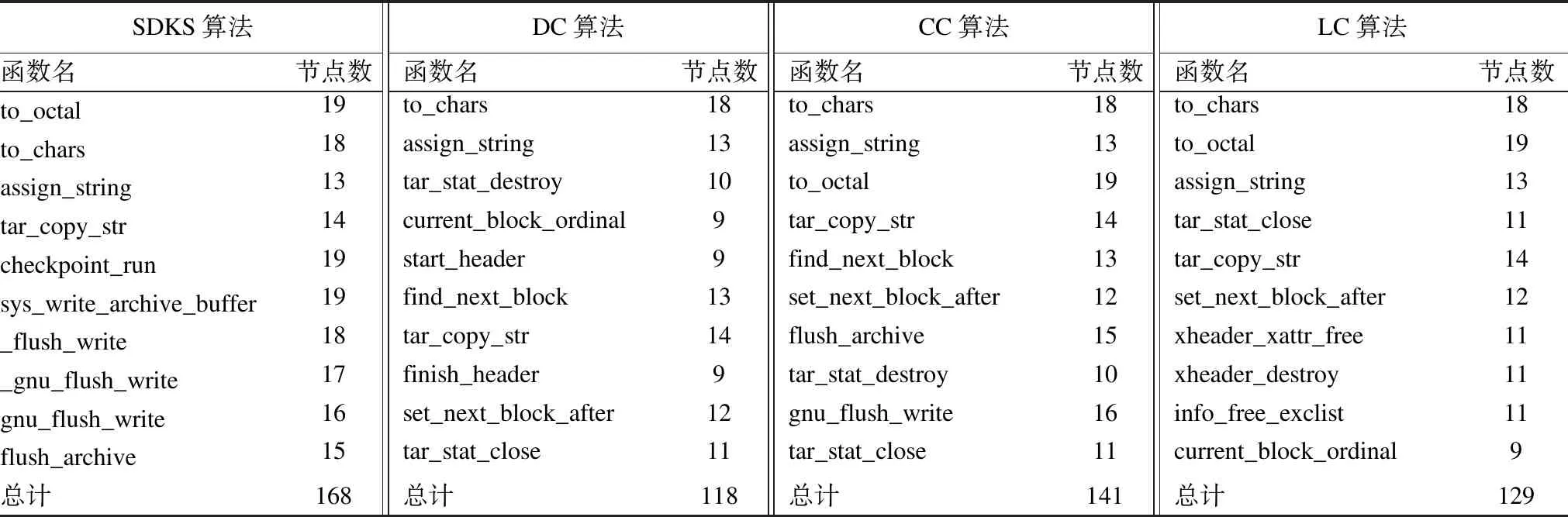
SDKS算法DC算法CC算法LC算法函数名节点数函数名节点数函数名节点数函数名节点数to_octal19to_chars18to_chars18to_chars18to_chars18assign_string13assign_string13to_octal19assign_string13tar_stat_destroy10to_octal19assign_string13tar_copy_str14current_block_ordinal9tar_copy_str14tar_stat_close11checkpoint_run19start_header9find_next_block13tar_copy_str14sys_write_archive_buffer19find_next_block13set_next_block_after12set_next_block_after12_flush_write18tar_copy_str14flush_archive15xheader_xattr_free11_gnu_flush_write17finish_header9tar_stat_destroy10xheader_destroy11gnu_flush_write16set_next_block_after12gnu_flush_write16info_free_exclist11flush_archive15tar_stat_close11tar_stat_close11current_block_ordinal9总计168总计118总计141总计129

5 总 结

本文基于复杂网络和结构熵思想研究软件动态执行行为及软件函数粒度级别的关键节点.考虑缺陷的产生和传播与软件网络节点间的关联有关,结合节点的全局出度和入度情况,提出节点面向缺陷产生的结构脆弱性和面向缺陷传播的结构传播性的计算方法,进而根据相对出(入)度值计算节点向下(上)子网络的结构熵及各全局平均结构熵,将满足平均结构熵的节点作为关键节点.在真实软件上进行实验并与经典中心性算法进行对比,通过SIR模型验证得出结论,本文提出算法在单个节点的排名上更加合理并且在各算法的前10名节点的总体结构脆弱性或传播性排名中,本文提出算法更具准确性.