基于卷积神经网络特征重加权的行人再辨识
2019-05-05王琳琳梁凤梅刘阿建
王琳琳,梁凤梅,刘阿建
(太原理工大学 信息与计算机学院,山西 晋中 030600)
1 引 言
行人再辨识的任务是匹配两幅由视野不重叠的两个摄机拍摄所得的行人图像[1],且成为计算机视觉方向的研究热点归因于其在监控视频中的广泛应用.然而,由于行人姿势、摄像机视角、光照等变化使得该任务极具挑战[7].如何提取既具鲁棒性又不失判别能力的行人特征成为行人再辨识的关键,且吸引了国内外大量学者的研究与关注.
近年来,基于卷积神经网络(CNN)的深度学习模型由于Krizhevsky等人[1]以较大的优势赢得ILSVRC-12挑战赛而流行起来.自动化研究所的Yi等人[2]先后将深度学习方法用于行人再辨识的研究中.
一般来说,行人再辨识的研究中主要采用两种类型的网络模型:基于样本对或三元组的验证网络模型.该模型由于早期公开的行人再辨识数据集较小而被广泛采用,如VIPeR[4],仅为每个身份的行人提供两幅图片.然而,基于siamese网络的验证模型或其变体未能充分利用数据集的标注信息[5],而仅考虑样本对或三元组是否属于同一身份.另一种极具潜力的是基于分类损失函数的分类模型.该模型最初应用在图像分类中[1],之后越来越受到行人再辨识研者的青睐得益于几个大数据集的公布,如CUHK03[6],Market1501[7].这使得训练一个更深的网络而不出现过拟合成为可能.
然而,很少有工作研究行人特征中每一维度信息对行人身份匹配结果判定的重要程度.我们认为特征的维度由于尺度差异在身份匹配中所起到的作用不同,不应在距离度量函数中平等对待.如行人特征中高跟鞋与粉色衣服的信息对行人性别的判定所起到的作用是不同的.如果我们在目标损失函数之前对学习到的行人特征进行重新加权,突出重要信息维度作用的同时,抑制无关维度的信息作用.其中权值矩阵在网络训练中根据目标函数自动更新.因此,特征中每一维度的值不仅可以转换到统一的尺度下,而且可以根据自己所包含信息的重要程度被区别加权.另外,类似于文献[9],我们对权值矩阵施加一个约束项,以提高行人特征的泛化能力.所不同的是,我们的验证子网络采用二分类的softmax损失函数而非马氏距离度量损失函数.Jin等人[10]设计了类似于我们工作的行人特征重加权层,但有两点本质区别:1)其特征重加权层在分类网络中,而我们的在验证网络中;2)其特征重加权层仅对每个维度单独加权,而没有将其他维度对该维度的影响考虑进去.事实上,我们无法保证特征维度之间是相互独立的,因此我们特征重加权层根据维度间的相关性对每一维度进行加权.如,行人特征中裙子与高跟鞋信息对性别判定所起到的作用是相互促进的.最后在几个行人再辨识数据集上的实验表明,我们采用的网络模型与设计的特征重加权层实验结果优于目前最好的几种方法.
2 siamese网络结构
本文的全局网络结构如图1所示,一个二分支的siamese网络结构,其中这两个分支分别与分类损失函数连接构成分类子网络,并且这两个分支联合起来与验证损失函数连接构成验证子网络.网络将正负样本对图像作为输入,经过一个权值共享的基本网络后,将图像特征输入到分类与验证子网络中.因此,我们的网络是在两种类型损失函数的联合监督下同时训练.
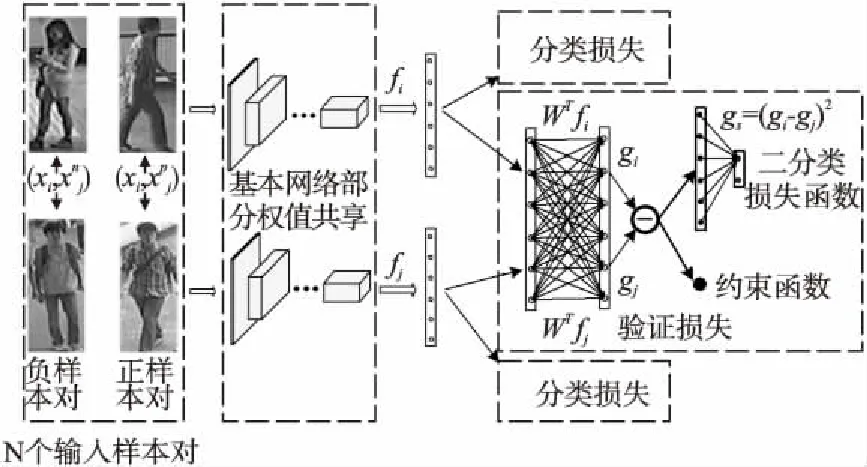
图1 全局网络结构Fig.1 Global network structure
2.1 分类子网络
当两幅行人图像特征fi,fj从基本网络中提取出来后,分别输入到分类子网络中.分类子网络在分类损失函数的监督下将行人再辨识的问题视为一个分类任务,直接学习一幅输入图像与其身份之间的非线性关系,表示为公式(1):
(1)
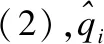
(2)
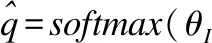
(3)
其中⊗表示卷积操作,分类损失函数采用交叉熵损失(softmax),定义为公式(4):
(4)
假设一个训练批次有N对样本(2N幅),fx∈Rd表示第x幅行人图像的特征(d维),身份为tx,Wi∈Rd为最后一个连接层权值矩阵W∈RD×M对应身份i的向量,b∈RM为偏置项,M为总身份数.
2.2 验证子网络
与欧式距离或马氏距离等度量损失函数不同,我们的验证子网络将样本对的验证视为一个二分类任务[7],但在接二分类的交叉熵损失层之前,需要对样本对进行如下操作:
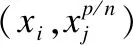
gs=(gi-gj)2
(5)

3 特征重加权层
如图2所示,query图像与其上方样本属于同一身份,与右方样本属于不同身份,我们以二维坐标来表示行人图像的特征.
假设第一维与第二维分别表示行人上衣与裤子特征属
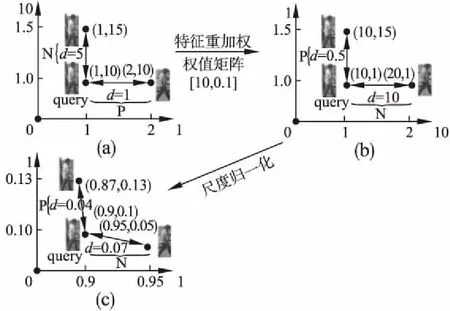
图2 特征重加权层的作用Fig.2 Role of weighted layers
性.如果我们认为这两种属性对行人身份的匹配作用相同,在
欧式距离的度量函数下,如图2(a)所示,由于正样本之间的距离为5,负样本之间的距离为1,最终导致错误匹配(特征距离越小则相似度越高).若我们对特征进行重新加权,分别强调上衣属性、抑制裤子属性对匹配的重要性,如图2(b)所示,正样本之间的距离为0.5,负样本之间的距离为10,得到正确的匹配.若我们对该层进行特征归一化,将得到同样正确的结果,如图2(c).
我们的特征重加权层由一个权值矩阵为W的全连接层实现.其中特征重加权矩阵为WT(权值矩阵W的转置),表示为公式(6):
g=g(WTf+b)
(6)
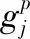
(7)
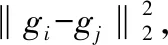
(8)
从公式(8)中知,若WWT为单位矩阵时,约束项变成特征fi,fj间的欧氏距离,特征重加权层完全失去作用.因此我们需要平衡特征重加权矩阵对欧式距离泛化能力的影响,将约束函数重写为公式(9):
(9)
其中λ为平衡系数,I为单位矩阵,当λ=0时,不计重加权矩阵对欧式距离的影响,当λ无穷大时,WWT逼近单位矩阵.
综上,我们的特征重加权矩阵在二分类验证损失与约束下自动更新权值.因此验证子网络的总损失函数为公式(10):
(10)

(11)
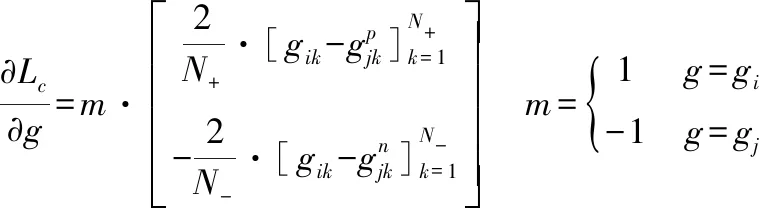
(12)
其中[·]为矩阵形式.
4 实验设置与结果
4.1 数据集
我们在四个行人再辨识数据集上进行实验,验证我们模型与方法的效果.分别为两个大数据集CUHK03与Market1501,两个小数据集VIPeR[4]与CUHK01[11].其中CUHK03与Market1501采用更接近实际应用的DPM检测器裁剪出的行人图像.除了Market1501数据集上的实验外,其他数据集实验均采用single-shot版本的测试方法,即测试集(gallery)中有且只有一幅与目标图像(query)同身份的行人图像.相应地multi-shot表示测试集中与目标图像同身份的行人图像有多幅.所有数据集训练与测试样本的划分均按照各自的测试协议进行.CUHK03、VIPeR与CHUK01分别报告重复20次、10次、10次实验的平均结果.
由于国际工程所在地的地理气候各不相同,而且不同地区的气候差异很大,气候条件对工程项目的影响也不容忽视。虽然一些极端气候会被视为不可抗力可以进行工期索赔,但一般来说,我国施工企业很难对世界各地气候进行精细化了解,因此在投标过程中难以全面考虑正常的气候影响因素。因此,一旦出现长时间降雨、干旱、冰冻等天气,而有无法达到不可抗力条件,此时会对施工企业造成一定影响。
4.2 数据输入准备
首先我们将所有数据集图像大小重置为128×48,并在送入网络之前减去均值图像(由所有训练集计算);然后,我们采用二维变换方式对训练图像进行7倍增广;最后我们打乱增广后的数据集并进行配对.我们采用文献[8]中的配对方式.
4.3 基本网络
为了验证我们模型与方法的普适性,实验在两个基本网络上进行,第一个采用文献[10]中的CNN,细节如图3所示,所有卷积层采用大小为3×3的滤波器,步长为1,边界用0填充;所有最大池化层采用大小为2×2的滤波器,步长为2;所有卷积层与全连接层后接批规范化层(Batch Normalization Layer),加速网络收敛.基本网络的最后一个全连接层输出512维的特征f.第二个基本网络采用文献[12]中的残差聚焦网络(Residual Attention Network,本文简称Attention).为了防止过拟合,本文采用Attention-39(39为网络深度).
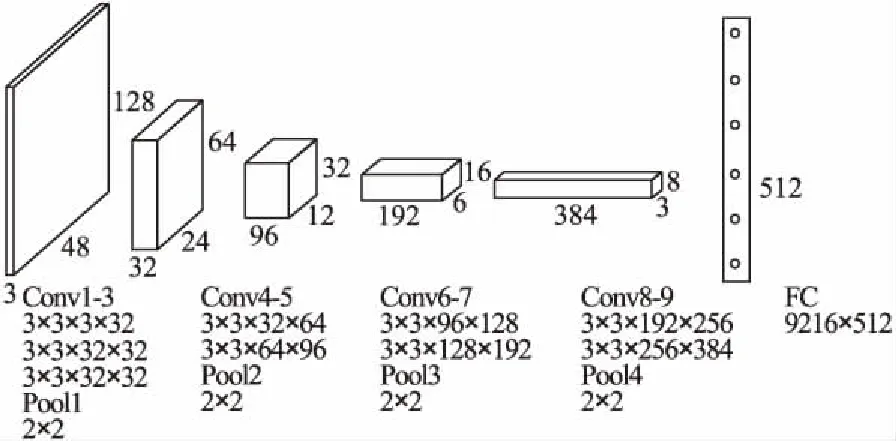
图3 基本网络CNNFig.3 Basic network CNN
4.4 训练设置
本文基于caffe深度学习网络框架采用GPU模式进行训练.其中GPU为内存12GB的NVIDIA Tesla k40c.初始学习率为0.0001,并在22k、32k次迭代后分别乘以0.1.最大迭代次数设置为38k,且网络训练基于Adam随机优化方法.我们首先计算分类子网络与验证子网络产生的反向梯度,并用两者的加权和更新网络,经过多次实验后确定权值分别为0.6与0.2,但在单独使用这两个子网络做对比实验时,权值都为1.网络每次训练的样本数(batch-size)设定为120(60对),权值衰减(weight_decay)为0.006.不做特殊说明时,特征重加权层的约束项平衡系数λ设定为0.01.
4.5 测试方法
给定一幅大小为128×48的行人图像,从基本网络中提取其特征f.计算每一幅目标行人图像特征与所有待测试图像特征之间的余弦距离.为了节省空间与方便比较,我们采用Rank-1-5-10的准确率代替CMC(Cumulated Matching Characteristics)曲线来评估所有实验的性能.与目前最好的且与本文工作相关的实验结果进行比较.另外,我们与文献[7]一致,同样采用mAP(Mean Average Precision)评估Market1501数据集上的实验结果.
4.6 实验结果
表1中“V、I、IV”分别表示单独使用验证网络、单独使用分类网络、联合分类与验证(本文)三种网络框架;“E、M、B”分别表示验证子网络采用欧式距离、马氏距离、二分类(本文)三种验证损失函数分;“W”表示我们的特征重加权层.从表1中的第一组实验(前三行)可以看出,单独使用验证子网络时,我们的二分类损失函数的优势更明显.因为欧式距离或马氏距离损失函数迫使同身份行人特征尽可能相似,这使得网络产生一定的过拟合现象,尤其在训练类别有限的情况下.
表1 CUHK03数据集上Single-shot模式的实验结果比较
Table 1 Comparison of experimental results for the Single-shot mode on the CUHK03 dataset

MethodRank-1Rank-5Rank-10CNN-V(E)48.660.373.2CNN-V(M)55.172.383.6CNN-V(B)63.480.788.4CNN-W-V(E)53.567.779.6CNN-W-V(M)54.670.281.5CNN-W-V(B)66.285.590.1CNN-I7592.195.9CNN-V(B)63.480.788.4CNN-W-IV(B)81.590.895.2Attention-39-I80.395.597.1Attention-39-W-IV(B)83.897.699.2LOMO+XQDA[17]46.378.988.6Gate-SCNN[18]68.180.988.3CNN-FRW-IC[14]82.196.298.2ResNet-50[10]83.497.198.7Deep Transfer∗[11]84.1--
第二组在第一组实验的基础上添加我们的特征重加权层,可以看出对于欧式距离与二分类损失函数,我们的特征重加权层使得对应的结果进一步提升,对于马氏距离损失函数,结果略有降低,因为马氏距离中的协方差矩阵与我们的特征重加权矩阵有一定的相似作用,因此累积加层只会让网络出现过拟合问题.从第三组实验中可以看出,结合分类与验证损失函数,结果要优于单独使用两者,因此我们结合这两种损失函数,使学习到的行人特征不仅是分开的,而且具有判别性.从第四组实验可以得出,Rank-1的准确率优于目前最好几种方法,除了我们的网络框架与特征重加权层外,得益于基本网络的聚焦机制.第五组为目前最好的几种方法的实验结果.
表2 Market1501数据集上实验结果比较
Table 2 Comparison of experimental results on the Market1501 dataset
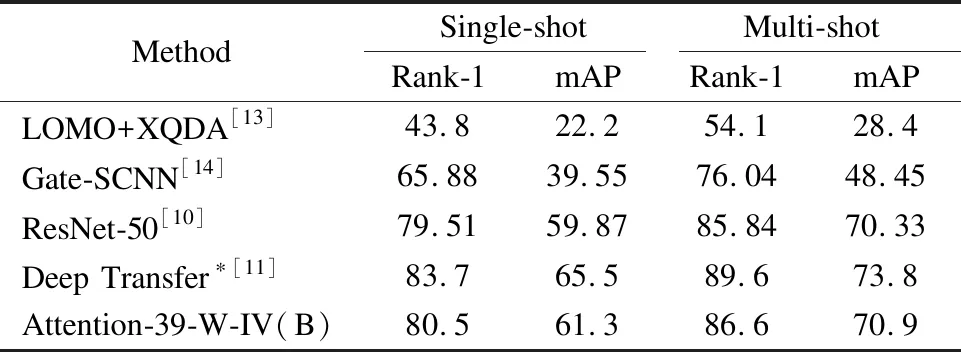
MethodSingle-shotMulti-shotRank-1mAPRank-1mAPLOMO+XQDA[13]43.822.254.128.4Gate-SCNN[14]65.8839.5576.0448.45ResNet-50[10]79.5159.8785.8470.33Deep Transfer∗[11]83.765.589.673.8Attention-39-W-IV(B)80.561.386.670.9
表2为Market1501数据集上的实验结果对比,我们的模型与算法不论是在single-shot还是multi-shot版本的测试协议下,都优于目前大部分的实验结果.表3为两个较小数据集上的实验结果对比.为了防止过拟合(训练样本不足),我们采用与文献[10]一致的联合训练方法.由于Deep Transfer*方法不仅在ImageNet数据集上预训练,而且采用两步转换学习,因此得到较高的准确率.
表3 VIPeR与CUHK01数据集上实验结果比较
Table 3 Comparison of experimental results on VIPeR and CUHK01 Datasets

MethodVIPeRCUHK01Rank-1Rank-5Rank-1Rank-5CNN-FRW-IC[14]50.477.670.590.0Deep Transfer∗[11]56.3-77.0-CNN-W-IV(B)51.878.371.292.5Attention-39-W-IV(B)53.580.172.492.8
为了验证约束项中平衡系数λ的作用,类似于文献[9]中对马氏距离约束项的探讨,我们用CNN-V(E)与CNN-W-V(E)两种网络模型进行实验.图4为CUHK03数据集上,7个
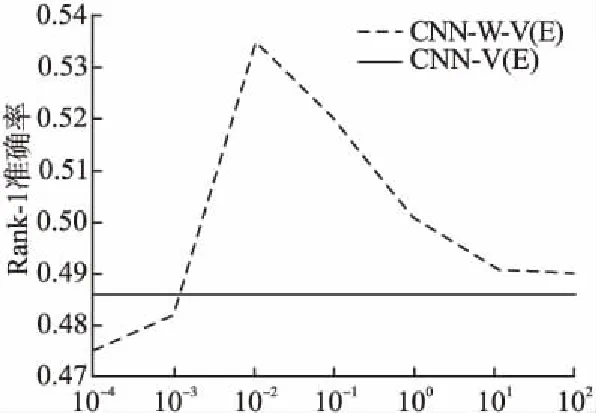
图4 不同λ值下CUHK03数据集上Rank-1准确率Fig.4 Rank-1 accuracy on CUHK03 datasets with different values
不同λ值对应的Rank-1准确率.从图中可以看出,当λ=0时,网络的泛化能力较弱,结果比欧氏距离损失函数的结果要差,说明单纯地加一个全连接层并不会提升准确率;当λ=100时,WWT趋近单位矩阵,因此与欧式距离损失函数的结果接近;λ=0.01时,我们的特征重加权层发挥出了自己的优势,结果明显优于欧式距离损失函数的结果.因此,一个合适的λ值可以平衡我们特征重加权层对欧式距离泛化能力的影响.
5 结束语
行人再辨识问题的研究中,为了使学习到的行人特征具有判别性,本文基于siamese网络模型结合分类损失函数验证损失函数联合监督行人特征的学习.除此之外,为了突出行人特征的每一维度对行人身份匹配结果的影响,我们设计一个特征重加权层,该层在网络训练中自动学习重加权矩阵而非人为设定.为了提高行人特征的泛化能力,我们对特征重加权层施加一个约束项,其中的平衡系数平衡重加权矩阵对欧式距离约束损失函数的影响.通过实验结果表明了本文模型与特征重加权层的优越性.
