基于键合图模型的SHA/EMA余度 系统的故障诊断

刘宏飞， 于黎明， 张柱， 阎旭栋， 韩旭东

(1. 北京航空航天大学自动化科学与电气工程学院, 北京 100083； 2. 北京航空航天大学 飞行学院, 北京 100083)

随着多电飞机概念的提出，功率电传作动系统开始越来越多地应用在飞机上，目前应用最广泛的两类功率电传作动器是电静液作动器(EHA)和机电作动器(EMA)。由于一些尚未解决的技术难题(如滚柱丝杠卡死)存在，功率电传作动器还不能完全取代传统的液压伺服作动器(SHA)，而是通常采用与技术成熟的SHA组合成非相似余度作动系统的方法来进行过渡[1]。非相似余度结构可有效地避免共性故障，但余度结构带来的元部件数量的增加会增加系统发生故障的可能性[2]，所以对传统液压作动器SHA与先进的功率电传作动器EMA组成的余度系统进行故障诊断具有一定的预研价值。

功率键合图是一种基于能量守恒原理的建模方法，可以方便地建立多能域系统的统一模型[3]。由功率键合图模型中的因果关系可以直接推导出反映系统故障特征的解析冗余关系式(ARR)，从而方便对系统进行故障诊断和隔离(FDI)。文献[4]应用全局ARR对不同工作模式下的混合动力液压转向系统进行了故障诊断。文献[5]采用双因果键合图方法增加了系统可隔离故障数量。文献[6]将键合图与BP神经网络相结合，研究了并网逆变器的故障诊断。文献[7]建立了EHA的键合图模型并对液压缸内泄漏故障进行了诊断。已有的研究多是针对系统中可隔离故障的诊断，对于不可隔离故障的诊断却鲜有提到，而在不可隔离故障中，某些典型故障仍然存在较大的诊断价值。

本文提出的基于键合图模型的故障诊断方法分为3步：第1步，建立SHA/EMA余度系统的行为模型，模拟系统的实际工作情况[8]；第2步，进行理论推导，得到故障诊断的理论依据；第3步，通过仿真对故障进行诊断。其中第2步最关键，完成该步骤后可以将系统中所有的故障分为可隔离故障和不可隔离故障，本文选择典型的可隔离故障(液压缸内泄漏、滚柱丝杠失步)和不可隔离故障(电液伺服阀内泄漏、滚柱丝杠卡死)进行了仿真验证。

1 行为模型

图1为SHA/EMA余度系统的原理图，图中上半部分为SHA，电液伺服阀控制液压缸输入流量驱动作动筒运动；下半部分为直驱式EMA，电机的旋转运动通过滚柱丝杠转化为直线运动。图中：iv为输入电液伺服阀的电流；U为输入电机的 电压；xs为滚柱丝杠的位移；xl和Fl分别为舵面的位移和其所受的负载力；xp为液压缸活塞杆的位移；FE和FH分别为滚柱丝杠与舵面间的作用力和活塞杆与舵面间的作用力。2个通道在舵面处采用力综合的方式，共同驱动负载。

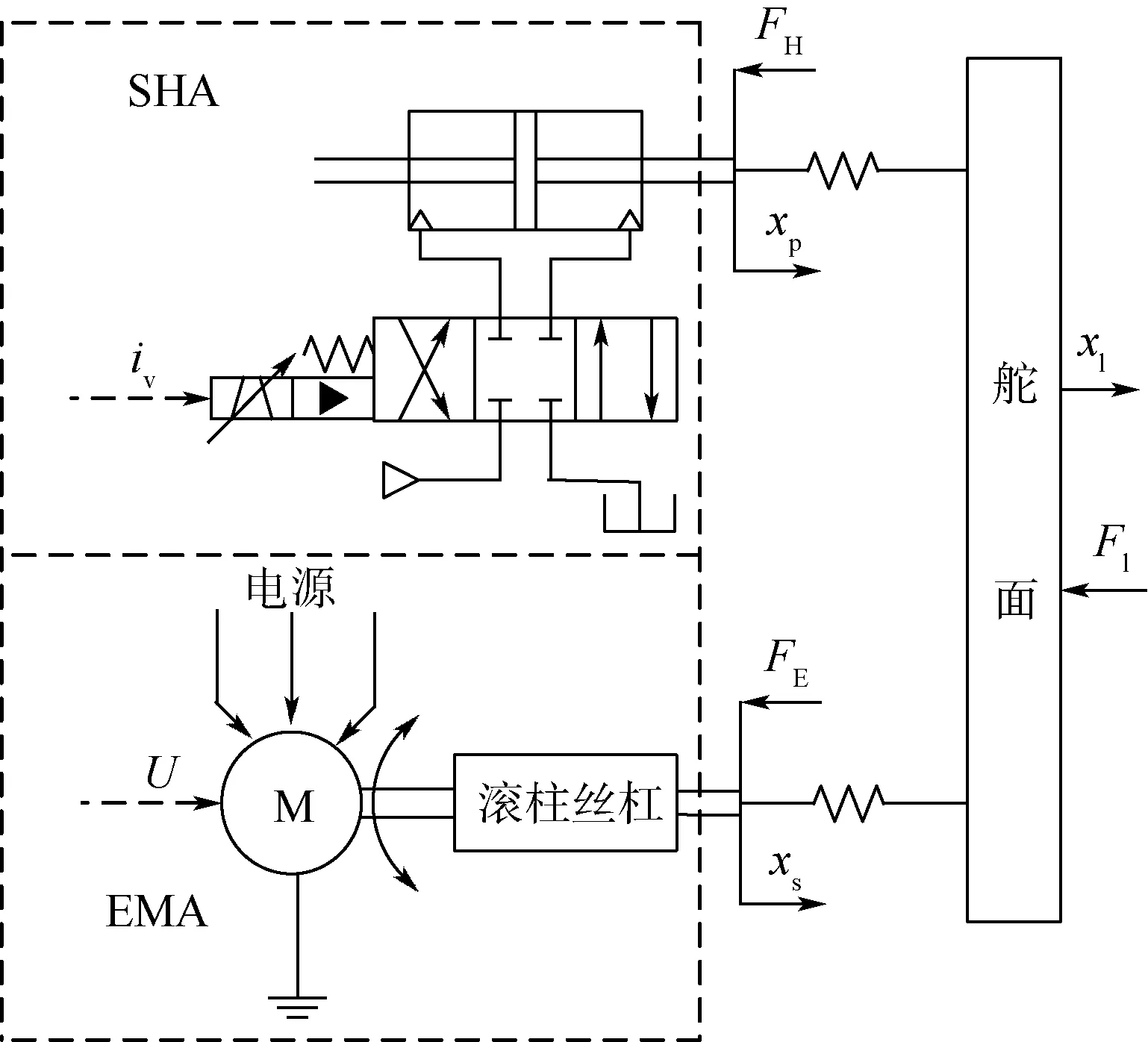
图1 SHA/EMA余度系统的原理图Fig.1 Schematic diagram of SHA/EMA redundant system

依次建立系统中电液伺服阀、液压缸、电机、滚柱丝杠和舵面的键合图模型，将其按照工作原理连接起来，得到SHA/EMA余度系统的键合图模型，如图2所示。为获得系统中所有的故障信息，在图2中设置了8个传感器Df1、Df2、De1、Df3、De2、De3、Df4和De4，分别测量电机的感应电流(Im)、电机转速(ω)、滚柱丝杠间的作用力(Fs)、滚柱丝杠移动速度(vs)、滚柱丝杠与舵面间的作用力(FE)、活塞杆与舵面间的作用力(FH)、活塞杆移动速度(vp)、液压缸两腔压力差(PL1)8个物理量。

建立了SHA/EMA余度系统的键合图模型后，需要验证该模型的可用性。查阅相关文献[9-10]，得到SHA和EMA的参数如表1所示。代入表1中的参数，对系统模型进行仿真验证。

SHA/EMA余度系统开环下的输出力曲线和位移曲线分别如图3和图4所示。由图3可知，SHA的响应速度快于EMA，最初EMA作为负载的一部分被SHA拉动，经过0.2 s后EMA才开始产生推力。由图4可知，SHA和EMA具有很好的同步性，位移偏差基本为零；在4 s处加入10 kN的外负载后，由于未加闭环控制，作动杆会被反推着运动，产生一定的反向位移，最终达到稳定状态。图3和图4中的曲线验证了该模型的可用性。

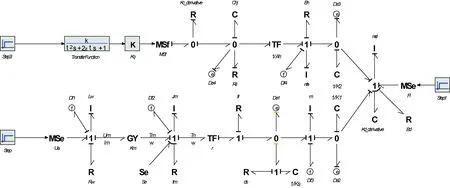
图2 SHA/EMA余度系统的键合图模型Fig.2 Bond graph model of SHA/EMA redundant system

表1 SHA/EMA余度系统的仿真参数Table 1 Simulation parameters of SHA/EMA redundant system

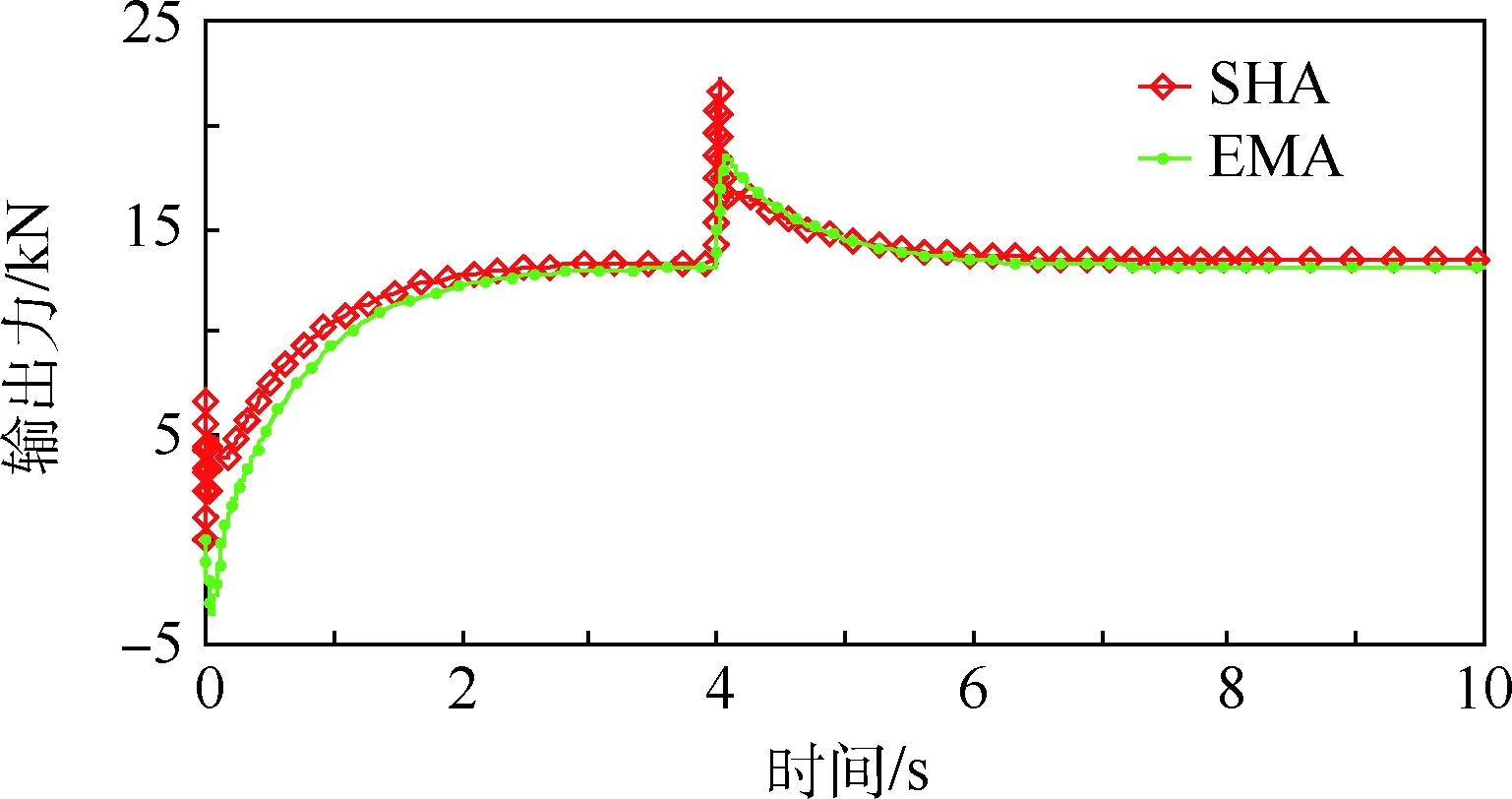
图3 SHA/EMA余度系统的开环输出力曲线Fig.3 Curves of open-loop output force of SHA/EMA redundant system

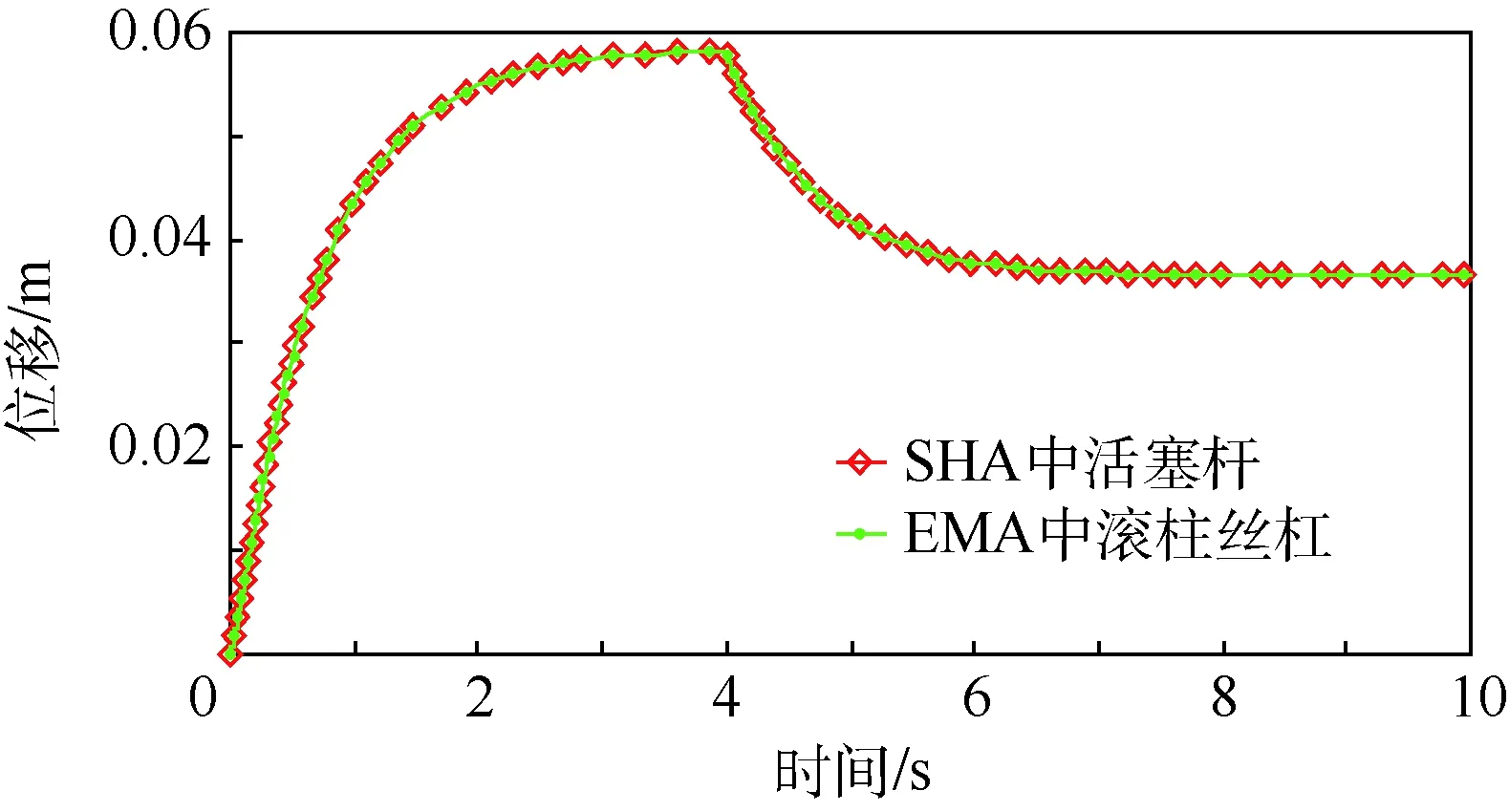
图4 SHA/EMA余度系统的开环位移曲线Fig.4 Curves of open-loop displacement of SHA/EMA redundant system

2 理论推导

故障诊断的理论推导分为3步：第1步，根据实际系统的行为模型建立诊断键合图模型；第2步，推导ARR，预测残差变化趋势；第3步，创建故障特征矩阵(FSM)，作为诊断依据。

2.1 诊断键合图

首先根据因果关系倒置法[11]，将图2中所有的储能元件(I,C)由积分因果关系变换成微分因果关系，然后将传感器变换成相应的虚拟源，最后修改其他键合图元的因果关系以避免冲突，由此即可得到SHA/EMA余度系统的诊断键合图模型，如图5所示。在该图中，虚拟源为诊断键合图的输入信号，其值来自行为模型传感器的输出值；与虚拟势(流)源相连键上的流(势)即为系统的残差，正常状态下其值都为零。为了方便2.2节中ARR的推导，这里给功率键指定了序号，图中一共有36根功率键。

2.2 解析冗余关系式

ARR是由已知变量(测量值和已知输入)表示的约束关系式，代表一组已知变量之间的各种约束关系[12]。ARR的数值即残差，在正常情况下，残差为零；发生故障时，残差不为零。SHA/EMA余度系统的诊断键合图模型中共有8个虚拟源，最多可以推导出8个ARR，推导过程中出现的ei(fi)表示第i根键上的势(流)。下面将依次对这些解析冗余关系式进行推导。

1) 电机感应电流的ARRf1

e1-e2-e3-e4=0

(1)

根据图5中各元部件的因果关系以及特性方程可知：

(2)

联立式(1)、式(2)消除方程中的未知变量，可以得到电机感应电流虚拟源处的解析冗余关系式(ARRf1)为

(3)

2) 电机角速度的ARRf2

e5-e6+e7-e8-e9=0

(4)

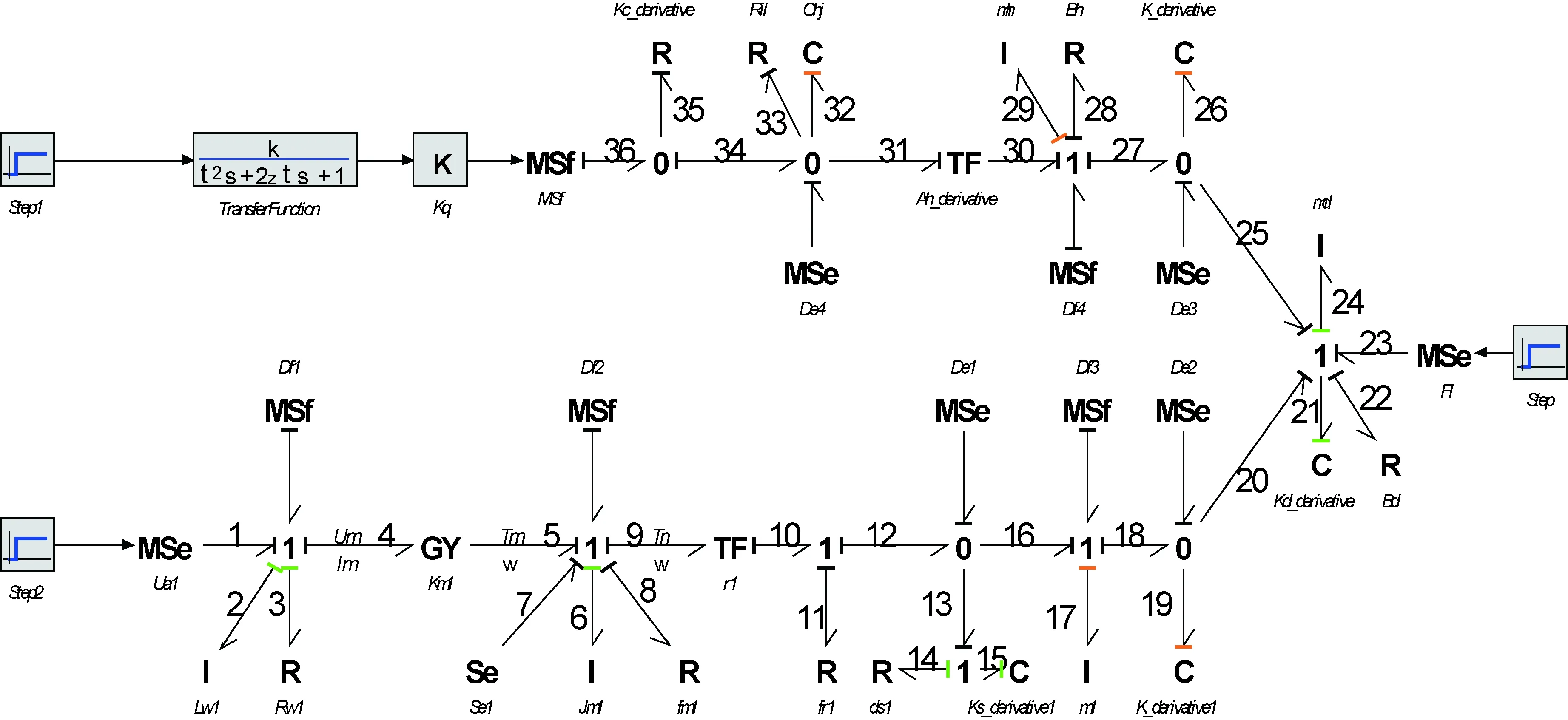
图5 SHA/EMA余度系统的诊断键合图模型Fig.5 Diagnostic bond graph model of SHA/EMA redundant system

根据图5中各元部件的因果关系以及特性方程可知：

(5)

式中:r为滚柱丝杠导程P与2π的比值。联立式(4)、式(5)消除方程中的未知变量，可以得到电机角速度虚拟源处的解析冗余关系式(ARRf2)为

(6)

3) 滚柱丝杠间作用力的ARRe1

f12-f13-f16=0

(7)

根据图5中各元部件的因果关系以及特性方程可知：

(8)

式中：ds为滚柱丝杠间的阻尼系数。

联立式(7)、式(8)消除方程中的未知变量，并在等式两边同时求导后可以得到滚柱丝杠间作用力虚拟源处的解析冗余关系式(ARRe1)为

(9)

4) 滚柱丝杠移动速度的ARRf3

e16-e17-e18=0

(10)

根据图5中各元部件的因果关系以及特性方程可知：

(11)

联立式(10)、式(11)消除方程中的未知变量，可以得到滚柱丝杠移动速度虚拟源处的解析冗余关系式(ARRf3)为

(12)

5) 滚柱丝杠与舵面间作用力的ARRe2

f18-f19-f20=0

(13)

根据图5中各元部件的因果关系以及特性方程可知：

(14)

式中：Bd为舵面等效黏性阻尼系数；Kd为舵面平稳负载的比例系数。

联立式(13)、式(14)消除方程中的未知变量，并在等式两边同时求导后可以得到滚柱丝杠与舵面间作用力虚拟源处的解析冗余关系式(ARRe2)为

(15)

6) 活塞杆与舵面间作用力的ARRe3

f27-f26-f25=0

(16)

根据图5中各元部件的因果关系以及特性方程可知：

(17)

联立式(16)、式(17)消除方消除方程中的未知变量，并在等式两边同时求导后可以得到活塞杆与舵面间作用力虚拟源处的解析冗余关系式(ARRe3)为

(18)

7) 活塞杆移动速度的ARRf4

e30-e29-e28-e27=0

(19)

根据图5中各元部件的因果关系以及特性方程可知：

(20)

联立式(19)、式(20)消除方程中的未知变量，可以得到活塞杆移动速度虚拟源处的解析冗余关系式(ARRf4)为

(21)

8) 液压缸两腔压力差的ARRe4

f34-f33-f32-f31=0

(22)

根据图5中各元部件的因果关系以及特性方程可知：

(23)

式中：xv为电液伺服阀的阀芯位移。

联立式(22)、式(23)消除方程中的未知变量，可以得到液压缸两腔压力差虚拟源处的解析冗余关系式(ARRe4)为

(24)

2.3 故障特征矩阵

诊断出故障后，需要确定系统的哪个部分出现了故障，这一过程称为故障隔离，故障隔离可以通过创建FSM来完成。FSM是一个二进制矩阵，描述了每个残差对物理设备、传感器，作动器和控制器中各种故障的结构灵敏度[13]。FSM可以直接根据2.2节所推导出的ARR构造，SHA/EMA余度系统的故障特征矩阵如表2所示。

表2中每一行的8个残差值(rf1～re4)组成对应参数的故障特征向量；最后2列Db和Ib分别表示故障的可检测性和可隔离性，取值为1表示故障可检测或可隔离。由表2可以看出，系统中所有物理参数引起的参数故障全部可检测，并且在单故障假设下有4组参数故障可隔离。可隔离故障有液压缸内泄漏(Ah,Ril)、液压缸阻滞(Bh)、电机失磁(Km)和滚柱丝杠失步(r,Ks)。

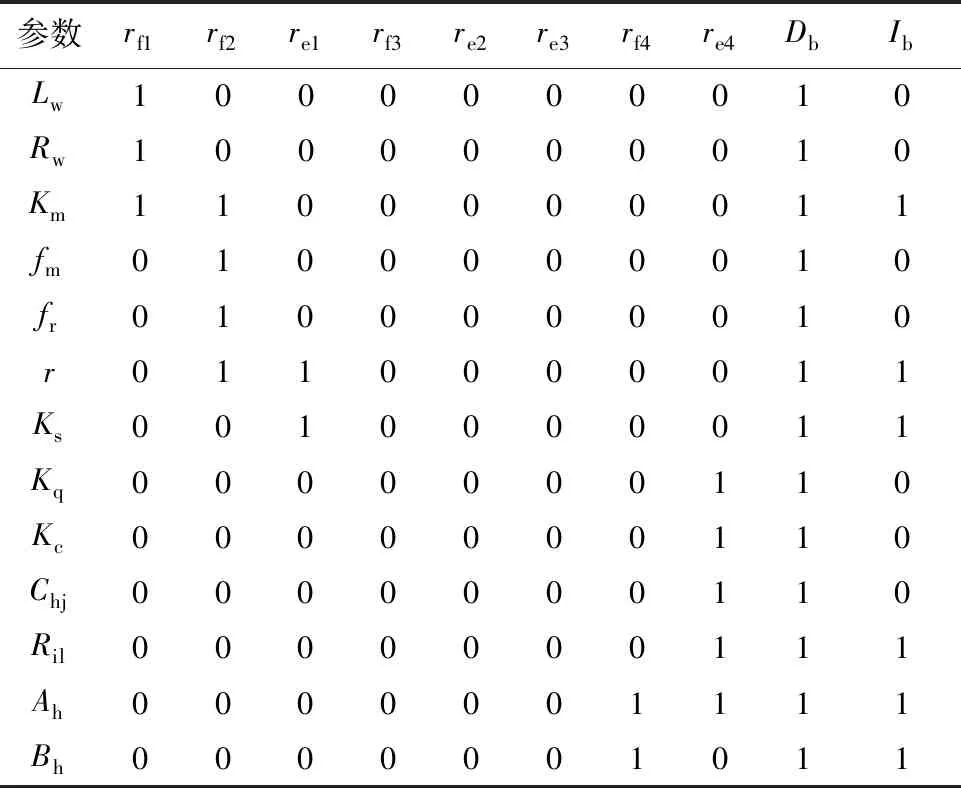
表2 SHA/EMA余度系统的故障特征矩阵Table 2 FSM of SHA/EMA redundant system

3 仿真分析

在单故障假设下，FSM将故障分为可隔离故障和不可隔离故障。可隔离故障可以直接使用诊断键合图来仿真验证，不可隔离故障将通过参数估计的方法对故障参数进行辨识。下面分别进行介绍。

3.1 可隔离故障

以可隔离故障中的液压缸内泄漏(Ah,Ril)和滚柱丝杠失步(r,Ks)为例进行仿真验证。将SHA/EMA余度系统的行为模型和诊断键合图模型联立，得到余度系统的故障诊断仿真模型，见图6。通过在系统的行为模型中改变参数值注入故障，测得图中8个虚拟源处的残差值，并将其组成故障特征向量后与FSM进行对比就能隔离故障。

系统无故障时的残差曲线如图7所示，该图显示系统中所有的残差值都为零，即故障特征向量[rf1,rf2,re1,rf3,re2,re3,rf4,re4]=[0, 0, 0, 0, 0, 0, 0, 0]，表示系统中没有出现故障，这与无故障假设相吻合。

1) 液压缸内泄漏(Ah,Ril)

液压缸内泄漏主要是由液压油中的杂质颗

粒在作动杆往复运动过程中磨损密封圈和筒壁后形成的缝隙造成的[14]，通过减小活塞有效面积Ah并且增大液压缸内泄漏系数Ril的值就能注入液压缸内泄漏故障。液压缸内泄漏故障的残差曲线如图8所示。

由图8可知，在这8个残差值中除了rf4和re4，其余6个残差值都非常小，可以忽略不计，则内泄漏故障对应的故障特征向量为[rf1,rf2,re1,rf3,re2,re3,rf4,re4]=[0, 0, 0, 0, 0, 0, 1, 1]，这与FSM中Ah和Ril的故障特征向量一致，表明液压缸内泄漏故障被成功隔离。

2) 滚柱丝杠失步(r,Ks)

滚柱丝杠失步主要由二者接触表面刚度下降或者磨损所引起[15]，与滚柱丝杠间的刚度Ks和传动比r有关，通过减小r和Ks的值可以注入失步故障，残差曲线如图9所示。

图9中显示，残差值rf2和re1不为零，其余6个残差值大小可以忽略不计，故障特征向量[rf1,rf2,re1,rf3,re2,re3,rf4,re4]=[0, 1, 1, 0, 0, 0, 0, 0]，与FSM中r和Ks的综合故障特征向量一致，说明滚柱丝杠失步(r,Ks)故障被成功隔离。

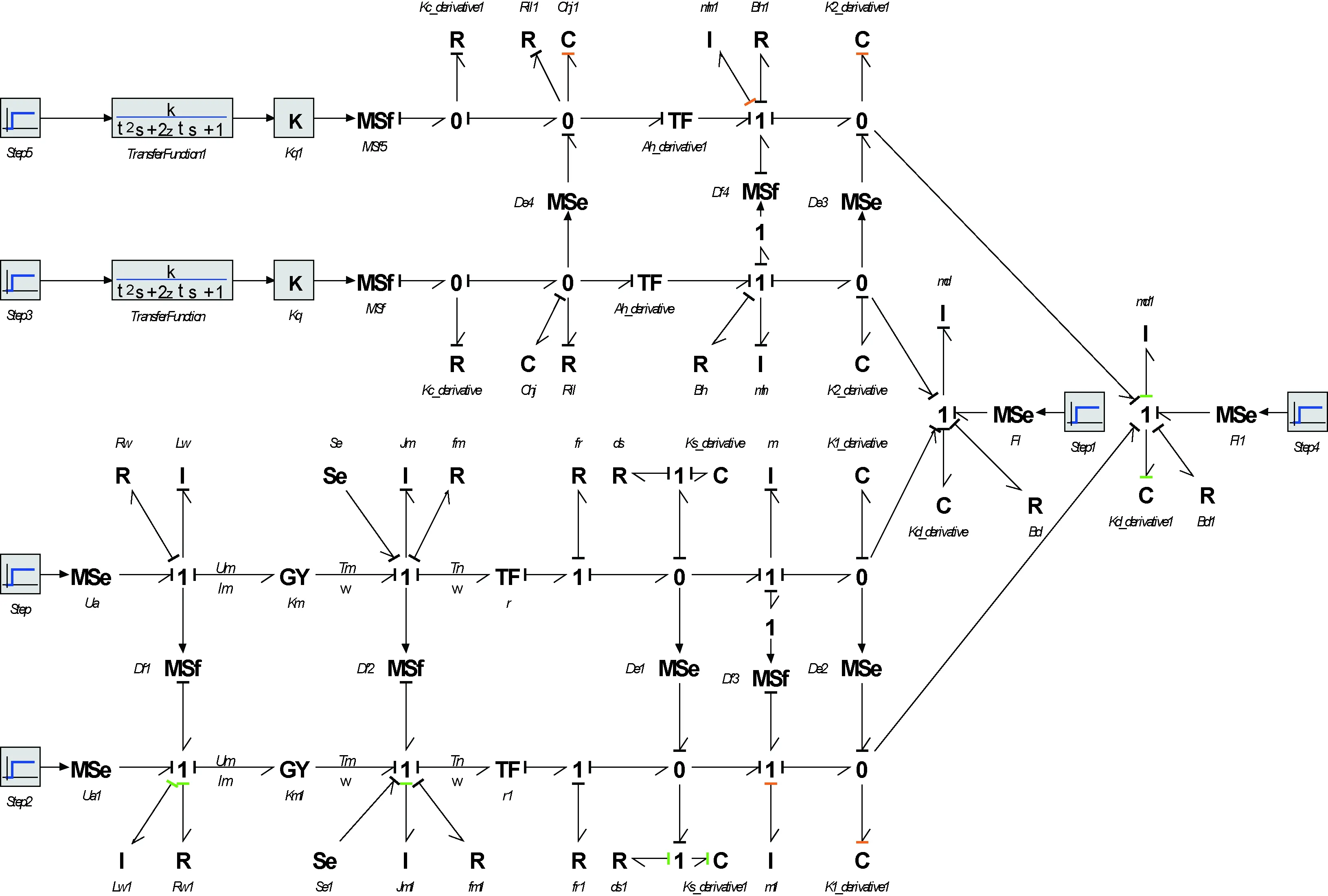
图6 SHA/EMA余度系统的故障诊断仿真模型Fig.6 Simulation model for fault diagnosis of SHA/EMA redundant system

3.2 不可隔离故障

FSM中除4组可隔离故障外，其余均为不可隔离故障。由于ARR是残差的计算式，利用ARR对故障参数进行参数估计可以诊断出不可隔离故障。下面对电液伺服阀内泄漏(Kc,Kq)和滚柱丝杠卡死(fr)这2种典型故障进行参数估计。

1) 电液伺服阀内泄漏(Kc,Kq)

电液伺服阀内泄漏故障主要是由于阀芯与阀

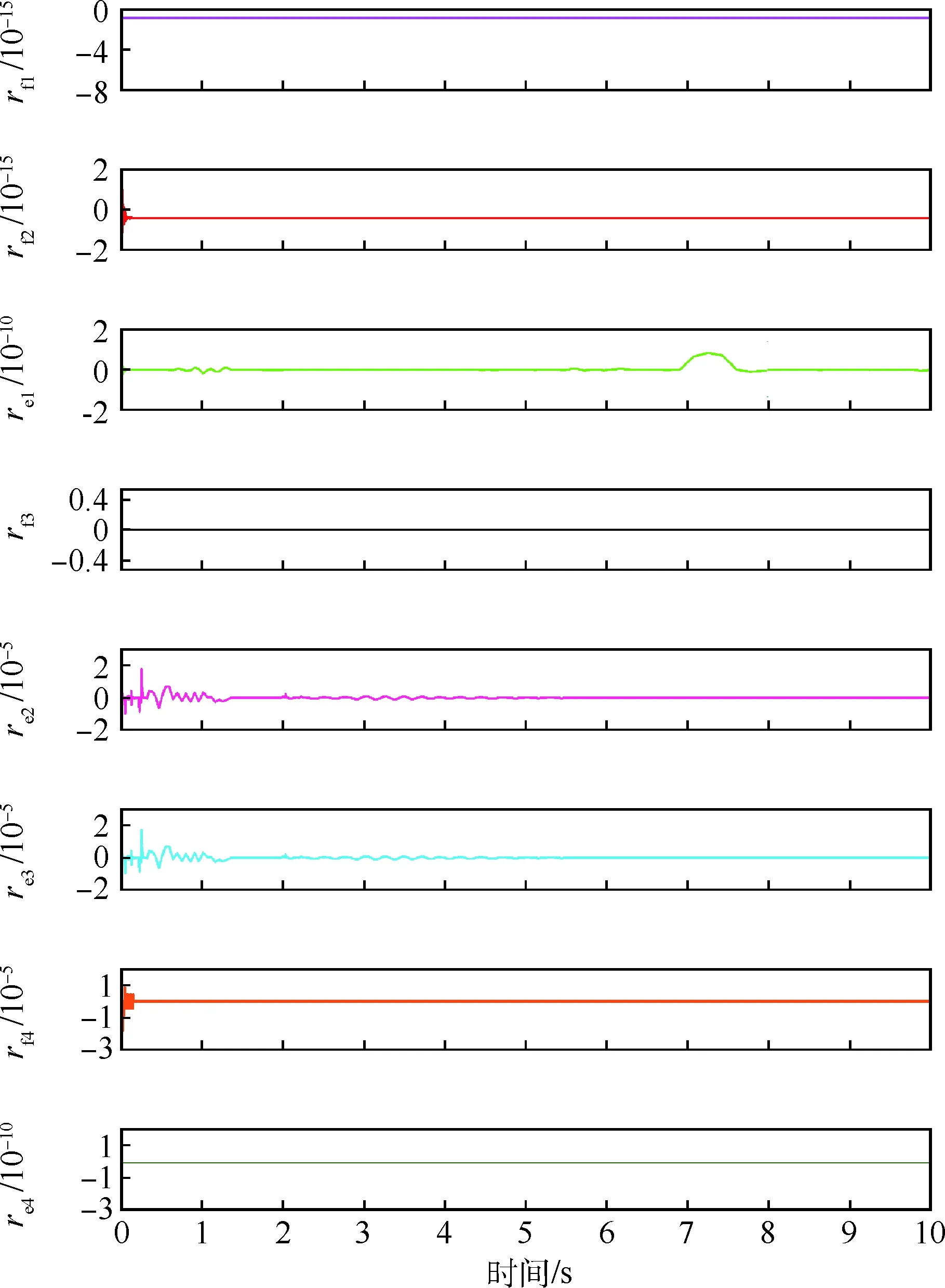
图7 SHA/EMA余度系统无故障时的残差曲线Fig.7 Residual curves of SHA/EMA redundant system without fault

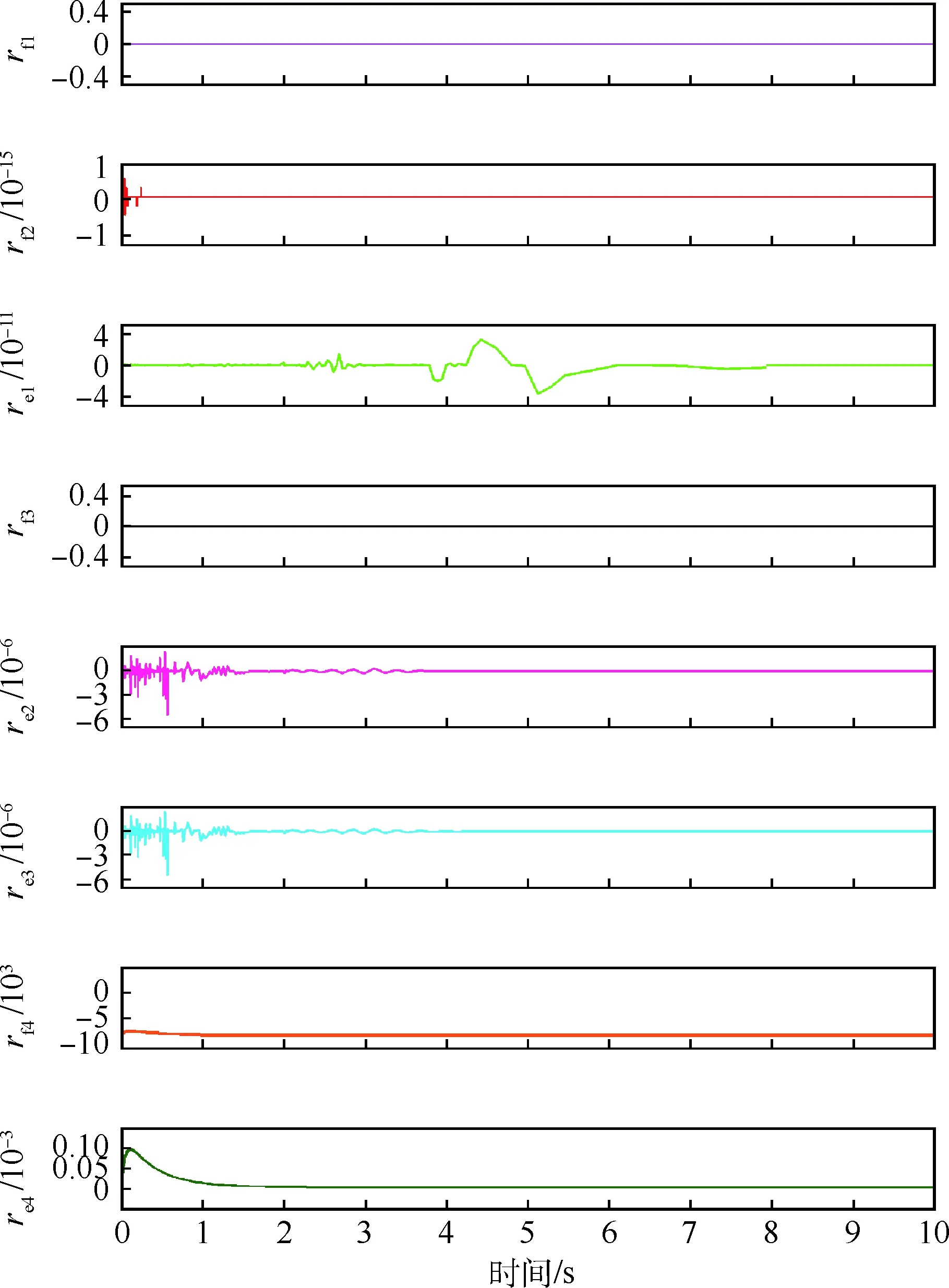
图8 液压缸内泄漏故障的残差曲线Fig.8 Residual curves of internal leakage fault in hydraulic cylinder

体间的磨损引起的，与电液伺服阀的流量增益Kc和流量-压力系数Kq有关，通过减小二者的值可以注入电液伺服阀内泄漏故障。对Kc和Kq所在的式(24)编写算法调用已知参数与传感器测量值，得到电液伺服阀内泄漏故障的参数估计结果如图10所示。

由图10可知，Kq和Kc的稳态估计值分别为2.65和1.723×10-11，其标称值分别为2.7和1.75×10-11，计算得出Kq和Kc稳态估计值的相对误差分别为1.85%和1.54%，均不超过5%，属于可接受范围，则电液伺服阀内泄漏的故障参数被成功隔离。

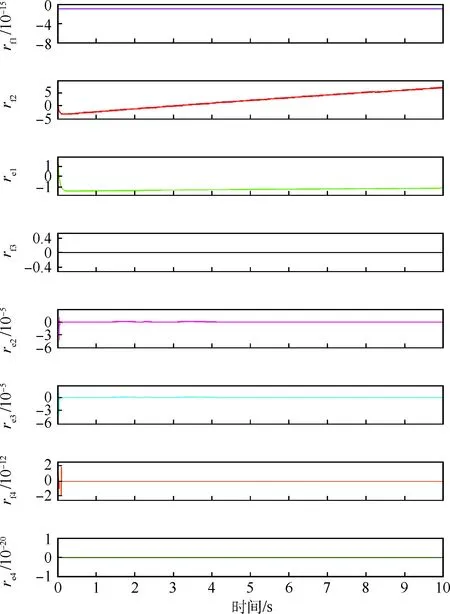
图9 滚柱丝杠失步故障的残差曲线Fig.9 Residual curves of out-of-step fault in roller screw

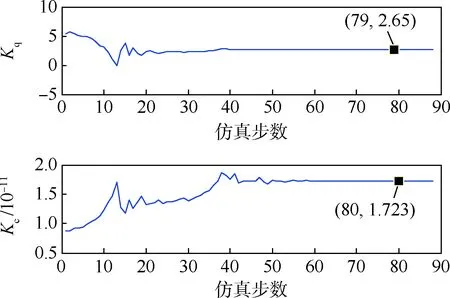
图10 电液伺服阀内泄漏故障的参数估计Fig.10 Parameter estimation of internal leakage fault in electro-hydraulic servo valve

2) 滚柱丝杠卡死(fr)

滚柱丝杠卡死主要是由于运动过程中有外物进入滚动体轨道或者受到外冲击所引起的，与滚柱丝杠间的黏性摩擦系数fr有关，通过增大fr的值可以注入滚柱丝杠卡死故障。对fr所在的式(6)编写算法调用已知参数与传感器测量值，得到滚柱丝杠卡死故障的参数估计结果如图11所示。

由图11可知，fr的稳态估计值为0.957 4×104，标称值为1×104，计算得出fr稳态估计值的相对误差为4.26%，不超过5%，属于可接受范围，表明滚柱丝杠卡死的故障参数被成功隔离。

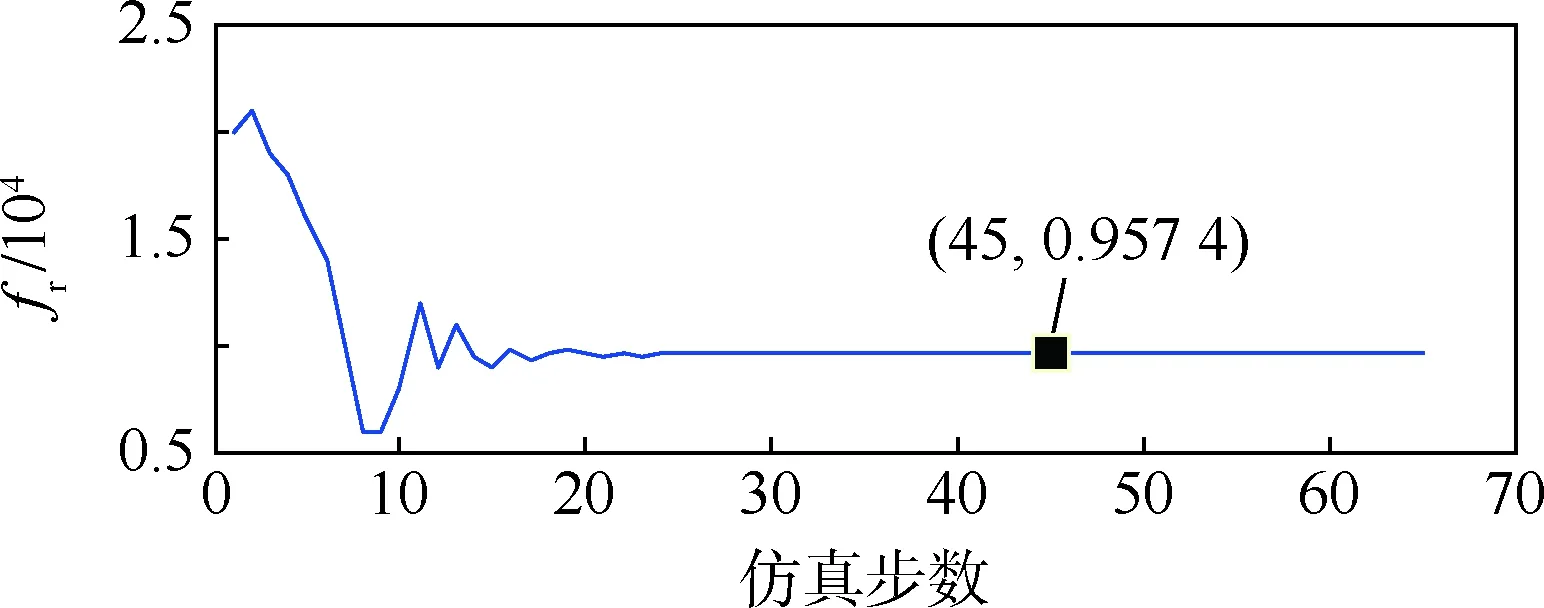
图11 滚柱丝杠卡死故障的参数估计Fig.11 Parameter estimation of jamming fault in roller screw

4 结 论

本文采用基于键合图模型的故障诊断方法，对SHA/EMA余度系统中的可隔离故障和不可隔离故障进行了诊断，仿真结果表明该方法是有效可行的。

1) 在可隔离故障中，得到液压缸内泄漏(Ah,Ril)和滚柱丝杠失步(r,Ks)的故障特征向量分别为[0, 0, 0, 0, 0, 0, 1, 1]和[0, 1, 1, 0, 0, 0, 0, 0]，与FSM一致，表明故障被成功隔离。

2) 在不可隔离故障中，电液伺服阀内泄漏和滚柱丝杠卡死的故障参数Kq、Kc和fr稳态估计值的相对误差分别为1.85%、1.54%和4.26%，均未超过5%，属于可接受范围，表明故障被成功隔离。