基于目标逃逸机动预估的空空导弹可发射区
2019-05-05王杰丁达理许明韩博雷磊
王杰, 丁达理, 许明, 韩博, 雷磊
(1. 空军工程大学航空工程学院, 西安 710038; 2. 中国人民解放军 95478部队, 重庆 401329;3. 国家电网陕西省电力公司电力科学研究院, 西安 710038)
无人自主空战代表着世界空军未来发展的必然方向,无人综合火力与控制技术作为其关键技术之一,是实现制导武器发射与稳定追踪的前提和基础。现有的有人机火控系统,在进行空空导弹火控解算时,均使目标保持直线定常状态或给定的机动状态,飞行员根据火控计算机提供的可发射距离参考值,基于当前态势,结合自身经验,综合判定导弹是否允许发射;无人机近距自主空战的条件下,由于决策回路中,不包含人在回路中的决策过程,且飞行员的经验知识难以准确量化,因而有人机的火控解算结果对于无人机而言并不适用。为了解决这一问题,必须对目标机的机动过程进行预估,使火控解算结果有助于提高空空导弹的命中概率,并适应无人近距空战中剧烈的态势变化。
空空导弹的火控解算结果,即为空空导弹的可发射区,它是导弹发射载机周围,目标初始位置的集合,一般通过目标与攻击机之间的相对距离进行表示。同一态势下,受导弹自身及目标运动状态等多种约束限制,存在导弹允许发射的最大距离和最小距离,进而构成可发射距离区间;在导弹离轴发射的条件下,目标与导弹的相对方位不同,存在的区间边值也不同,这些区间的左右边界值分别构成可发射区的近边界和远边界,远边界、近边界及由边界临界值对应的距离区间形成的侧边界在空间内可构成一个封闭的包络。当目标初始位置位于该包络内,导弹能够以一定的概率命中目标。近年来,针对空空导弹可发射区问题,国内外学者主要从空空导弹可发射边界的预测[1-2]、双机或编队条件下的协同可发射区[3-4]、导弹发射后的动态可发射区[5-6]等方面进行研究。这些文献对可发射距离解算时,均使目标保持原运动状态或设定的机动状态,而针对目标机动预估的空空导弹可发射区至今尚无公开文献涉及。
本文从目标机动行为的角度出发,基于追逃对抗策略,设计了目标机动预估系统。将导弹发射后,目标的机动过程简化为逃逸机动过程,进而抽象为逃逸对抗过程,目标根据导弹的方位信息执行逃逸机动决策,以此实现对目标机动信息的预估。在对敌机机动行为预估的基础上,通过黄金分割搜索策略实现对导弹可发射边界值的快速精确求解。
1 导弹可发射问题的解算原理
导弹可发射问题的解算过程需要融合考虑导弹性能、目标运动状态和攻击机运动状态的影响。首先,确定目标运动状态信息;然后,解算系统根据导弹与目标的相对状态,基于多约束条件下运动动力学模型,进行导弹的攻击弹道解算;最后,根据脱靶量判定导弹是否命中目标。基于当前弹道解算结果,搜索算法对距离搜索初值进行更新,并对上述过程进行迭代运算,最终输出由最大距离Rmax和最小距离Rmin构成的距离区间范围[Rmin,Rmax]。
为了有效地求解空空导弹可发射区边界包络,需要对攻击机周围目标的位置进行搜索。导弹受发射时刻导引头视场搜索能力的制约,存在最大离轴发射角。在离轴发射角所允许的范围内,标定当前目标进入角,可计算出不同目标离轴发射角条件下的可发射距离区间,这些距离构成的集合即为导弹的可发射区。可发射区表征了基于一定态势下的导弹的整体攻击能力,考虑到空战对抗中导弹的作战使用实际,本文将其数学模型表述为
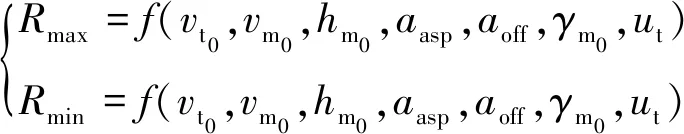
(1)
式中:vt0和vm0分别为发射时刻目标机速度和导弹初速度;hm0为导弹发射高度;aasp为离轴发射角;aoff为进入角;γm0为导弹发射倾角;ut为目标机动操控量,在目标保持原状态,即定常直线运动状态的情况下,ut保持为定值。在本文提出的基于目标机动预估的可发射区解算时,目标操控量依据相对态势实时变化。
发射时刻,目标与导弹的相对状态信息通过离轴发射角aasp和进入角aoff进行描述。离轴发射角是指目标与导弹质心连线偏离导弹轴线的角度,进入角指目标速度方向与导弹速度方向的夹角。为了便于计算和空间表示,假设攻击机速度方向与机身轴线方向一致,将上述2个角度分别投影到水平和垂直2个方向,定义其公式为
(2)
式中:β0和ε0分别为发射时刻的视线偏角和视线倾角;ψm0、γm0和ψt0、γt0分别为发射时刻导弹和目标机的航迹偏航角、航迹俯仰角。某发射时刻,攻击机与目标机的相对态势与对应角度关系如图1所示,由于发射时刻,导弹与攻击机固连,因 而导弹-目标的位置角度关系与攻击机-目标机之间的位置角度关系是一致的。
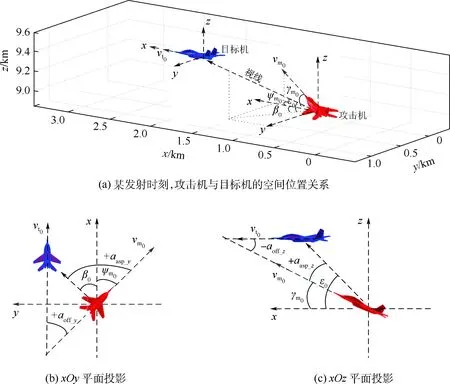
图1 某发射时刻攻击机与目标相对位置、角度关系示意Fig.1 Schematic diagram of relative position and angle between attacker and target at a launch moment
2 基于追逃对抗策略的目标机动预估系统构建
传统的可攻击区解算时,将导弹发射后目标的运动过程看作一个静态的过程,即导弹攻击过程中,目标保持当前状态或给定的机动状态,以此进一步计算导弹可发射边界。由于未能考虑导弹发射后,目标机为摆脱导弹攻击而可能实施逃逸机动的状态实际,因而在目标飞行操控保持恒定的前提下,所解算的可发射区,难以适用于无人近距空战中高动态的态势变化。为解决这一问题,必须对目标机动状态进行预估。考虑到精确预测目标的机动状态十分困难,本节从目标机动行为的角度出发,模仿人在回路中的决策方式,将导弹发射后目标机动过程视为目标机与空空导弹之间的动态博弈对抗过程,目标飞行操控量依据与导弹的相对态势动态变化,实施机动以使自身态势占优或摆脱当前导弹追踪的状态,从而将机动预估问题,转化为逃逸决策问题。从导弹的战术使用性能与追踪机理角度,构建基于追逃对抗策略的目标机动预估系统,实现对目标机动状态的预估。
2.1 目标机平台质点模型
令状态量和控制量分别为[xt,yt,zt,vt,γt,ψt]T和[ntx,ntz,μt]T,构建目标机质点运动动力学模型[7]为
(3)
式中:(xt,yt,zt)为目标机在惯性坐标系的位置;vt、ψt和γt分别为目标机速度、航迹偏航角和航迹俯仰角;g为重力加速度;ntx和ntz分别为目标机切向和法相控制过载;μt为滚转角。
2.2 目标机动动作库构建
为了准确描述目标机机动行为,并考虑到决策系统的快速性,目标机采用NASA学者提出的基于7种基本机动方式的机动方法[8]。如图2所示,基于目标机平台性能,采用极限操纵[9]的形式,将最大加力加速飞行、最大过载左右转弯、最大过载爬升或俯冲等7种基本操纵方式作为目标机逃逸机动的备选项。
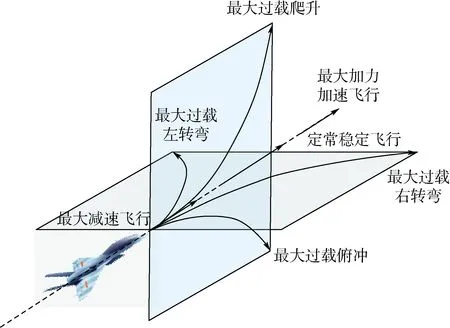
图2 典型机动动作库Fig.2 Typical maneuver library
2.3 逃逸机动评价函数设计
导弹攻击飞行过程中,导引头离轴发射角,即动态视场角是主要限制因素,直接影响导弹的跟踪能力;导弹受限于自身燃料限制,在追踪过程消耗的时间越长,空空导弹可发挥的机动性能就越弱;且一般而言,导弹脱离载机后,在自身发动机的瞬时推动下,获得更大的加速度,使导弹飞行速度远远大于目标飞行速度。因此,目标逃逸机动过程中,应将相对角度、相对距离作为决策判断的主要态势因素。
导弹-目标追逃机动过程中,导弹与目标机间的相对位置关系如图3所示。图中,下标m表示导弹,t表示目标机;r为导弹与目标机的距离矢量;vm和vt分别为导弹和目标机速度;ϑm和ϑt分别为导弹和目标机的提前角[10],即速度矢量与目标视线的夹角。定义:
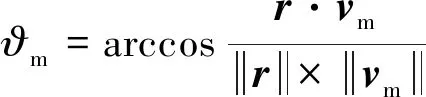
(4)
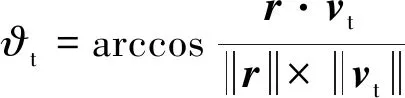
(5)
r=[xt-xm,yt-ym,zt-zm]T
(6)
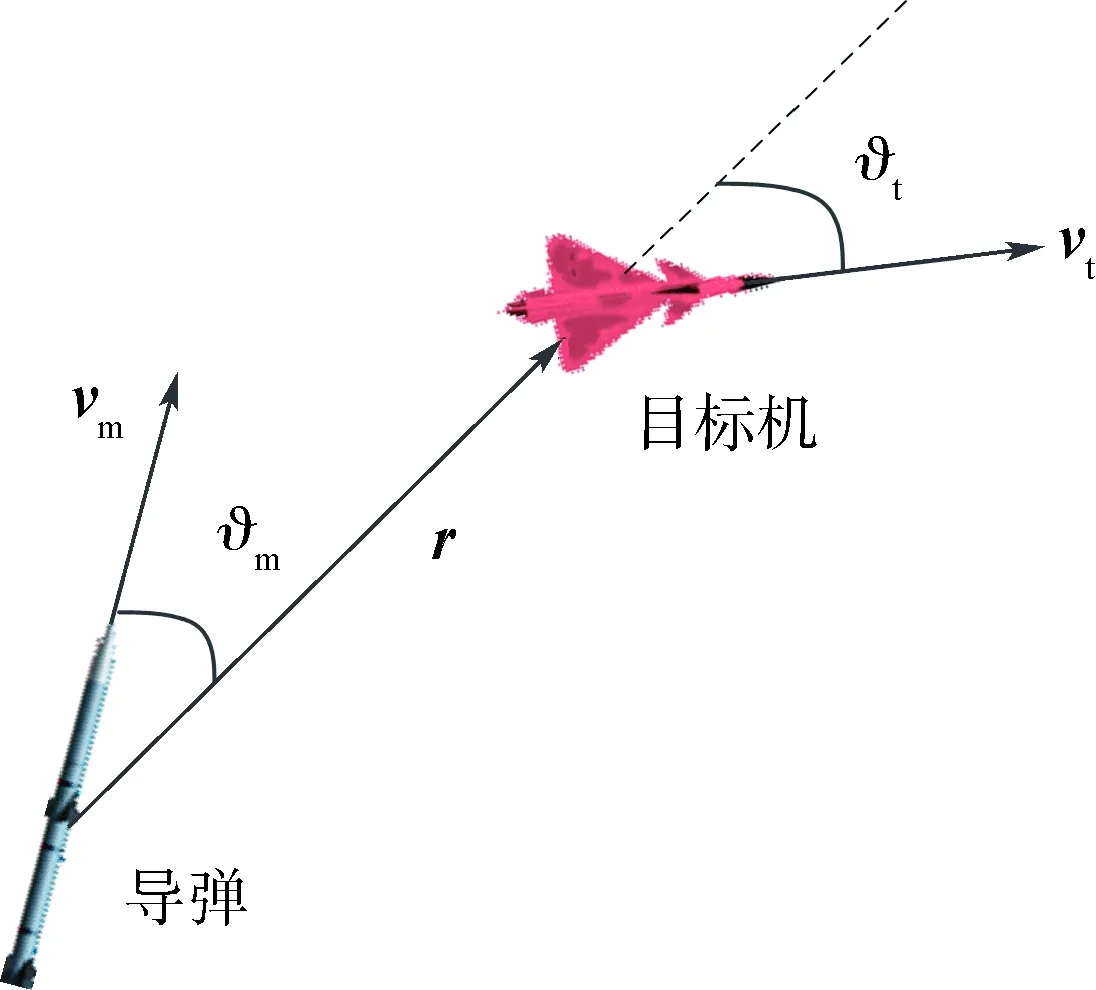
图3 导弹-目标相对参数示意Fig.3 Schematic diagram of relative parameters between missile and target
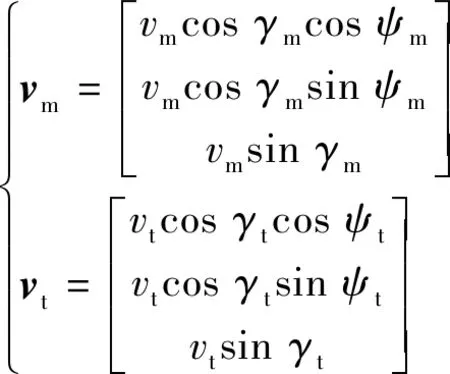
(7)
2.3.1 角度因子评价函数
角度因子是导弹追踪过程中最为重要的因素。目标机位于导弹动态视场角,即离轴发射角,允许的范围内是导弹能够搜索、稳定追踪和命中目标的基本前提。目标机位置位于导弹离轴搜索范围之外,即导弹提前角大于导弹允许的动态视场角时,导弹将丢失目标。因而增大导弹提前角是目标逃逸策略的优先选项。假定导弹发射后,最大离轴发射角为φD,构建目标机逃逸决策角度因子为
(8)
式中:κa为角度修正因子[10]且κa≥1,用以提高逃逸决策的可靠性;τ为一个很小的正常数,用于适应导弹提前角恰好等于最大离轴发射角的情况。
2.3.2 距离因子评价函数
导弹攻击过程中,受限于多种因素限制,存在最大最小攻击距离。一方面,追逃过程中,相对距离越大,追逃时间就越长,导弹机动优势逐渐减弱;同时,目标机机动的决策时间越长,逃逸机动的准备就越充分,有利于目标机自身性能的充分发挥。另一方面,受限于导引头探测信号接收能力、相对接近速度及制导指令时间要求等限制,存在最小攻击距离。当相对距离小于最小攻击距离时,导弹无法攻击目标。一般而言,考虑到人的应激行为,以及航炮等近距攻击武器的威胁,应将扩大相对距离作为逃逸策略的主要选项。因而,构建距离因子为
(9)
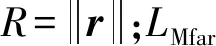
2.3.3 逃逸机动决策整体评价函数
逃逸机动决策整体评价函数的作用是对目标机机动方案进行评价。综合角度和距离2个决策因子,构建逃逸机动决策整体评价函数为
(10)
式中:w1、w2为决策因子权重,设定w1>w2,且w1+w2=1。
2.4 基于统计学原理的逃逸机动决策方法
为了克服逃逸机动决策中,导弹位置信息不确定给目标逃逸机动决策造成的影响,本文采用文献[11]提出的基于统计学原理的鲁棒机动决策方法,基于当前空空导弹与目标机的状态信息,将动作库中的所有动作的控制指令送入目标机质点模型,进行机动试探,通过逃逸机动决策整体评价函数(期望)和各决策因子的方差综合判定,收益值最高的方案就是目标机逃逸机动即将执行的方案。其具体流程在文献[11]中有详细的论述。
图4给出了导弹发射时刻,攻击机高度为8 000 m,导弹发射倾角为0°,目标离轴发射角aasp_y=aasp_z=0°的条件下,不同进入角的几种典型情况对应的导弹-目标的追逃机动轨迹仿真结果。其中蓝色轨迹为目标逃逸机动决策下的机动轨迹,即目标机动状态的预测轨迹;红机为攻击机,红色轨迹为基于比例导引法的空空导弹追踪轨迹。可见随目标进入角的不同,目标逃逸机动行为存在较大差异;整体来看,逃逸趋势沿扩大提前角或扩大相对距离的方向发展,这与预期是一致的。
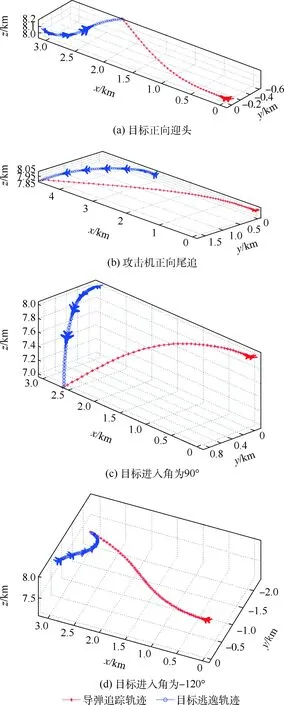
图4 典型情况下导弹-目标追逃机动仿真轨迹Fig.4 Simulated tracking and escaping maneuver trajectory between missile and target under typical condition
所构建的目标机动预估系统,将导弹发射后的追踪过程视作一个追逃对抗的过程。根据当前的态势信息,通过逃逸机动决策整体评价函数,在基本机动动作中选择最优的控制量,实现目标机逃逸决策。通过逃逸决策的方式实现对目标逃逸机动行为的预测,最终将逃逸机动的决策结果,作为目标机机动方式的预测输出结果。基于最优值理论,所预测的目标机动轨迹是于导弹追踪最不利的,与目标机而言是最有利的。即便目标不采取这种方式,导弹追踪效果将朝向更有利于导弹追踪的方向发展,对于攻击距离解算结果而言仍然是有效的,因而所构建的目标机动预估系统具有更广泛的意义。
3 多约束条件下空空导弹运动动力学建模
3.1 空空导弹运动动力学模型
惯性坐标系下,导弹运动学方程为
(11)
式中:(xm,ym,zm)为导弹在惯性坐标系下的坐标;vm、γm和ψm为导弹的速度、航迹俯仰角和航迹偏航角。
弹道坐标系下,导弹的质点动力学方程为
(12)
式中:Pm和Qm分别为导弹的推力和空气阻力;Gm为导弹的重量;nmc和nmh分别为导弹在偏航方向和俯仰方向的侧向控制过载。
Pm、Qm和Gm的变化规律为[3]
(13)
(14)
(15)
3.2 导弹导引控制模型
导弹参照文献[13]提出的比例导引律,并假设在相互垂直的2个控制平面内导引系数均为K,偏航和俯仰方向的2个侧向控制过载定义为
(16)
(17)
(18)
导弹刚离开载机时,为保证载机安全和导弹顺利达到超声速、防止失控,存在非可控飞行时间t0。在该时间内,制导电路不产生控制指令,导弹做自由飞行;考虑导弹结构稳定性,导弹侧向需用过载不应突破导弹最大可用过载nmax限制。故导弹实际控制过载表示为
n=
(19)
式中:n1为侧向需用过载;tc为导弹最大可控飞行时间。
3.3 导弹性能约束条件分析
导弹命中目标可定义为[3]:R≤e且t≥tyx。其中e为保证战斗部有效杀伤的脱靶量;tyx为导弹引信解除保险时间。
导弹性能约束制约着发射区的范围,当导弹与目标的相对状态突破导弹性能约束时,将判定导弹脱靶。为了准确描述导弹的跟踪状态,基于导弹战术应用实际,对导弹性能约束分析如下:
1) 导引头动态视场角限制。如第2节相关内容所述,导弹发射后,当导弹-目标视线偏离导弹轴线的角度(即提前角),突破动态视场角限制时,导引头将丢失目标。同时,发射时刻,受限于导发架固连的影响,发射时刻最大动态视场角较发射后略小,发射时刻的提前角亦不应突破该角度限制,即
(20)
2) 导弹最大飞行时间tmax限制。当飞行时间大于导弹最大飞行时间时,导弹自毁。即
t≤tmax
(21)
3) 目标影像探测距离限制。对于红外型空空导弹,初始制导时刻,导弹相对目标距离小于目标影像最小探测距离Rmin时,目标影像尺寸过大,调制盘寻的部分失去调制作用,不能形成探测信号,导弹失控。即
(22)
式中:η是个很小的数。
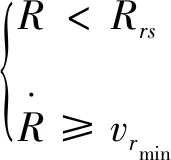
(23)
式中:Rrs为相对距离判断值。
除此之外,导弹需要满足的约束还应包括:载机雷达可探测距离限制、导引头跟踪角速度限制、高度限制、导弹最小可控速度限制、战斗部有效起爆区限制等,考虑到文章篇幅限制,在此不做详细论述。
4 基于黄金分割搜索算法的可发射边界求解策略
4.1 黄金分割搜索策略的解算原理
在一维搜索中,黄金分割搜索算法[14]具有不需要预先知道搜索循环次数、收敛速度快的优点,因而在描述可发射区解算问题的文献[3,15]中得以广泛应用。以最大可发射距离Rmax为例,在目标进入角aoff及导弹发射倾角γm0已知的情况下,其基本解算步骤可表述为
1) 以攻击机为中心,在导弹离轴角发射允许的范围内,确定目标初始位置相对于载机的方向,即目标离轴发射角aasp。
2) 预估初始搜索距离为[a0,b0],计算黄金分割点Rg0=a0+0.618(b0-a0)。
3) 以分割点位置为目标初始位置,由所构建的目标机动预估系统实时输出目标飞行操控量ut;导弹由初始位置对该目标进行追踪,根据导弹性能约束判断导弹是否命中目标,本文所构建的基于目标逃逸机动预估的导弹追踪弹道解算逻辑如图5所示。
4) 如命中目标,令a1=Rg0,b1=b0;如未命 中,则令a1=a0,b1=Rg0;重新循环计算,直到求出满足约束|bi-ai|<δ的边界为止,其中δ为解算精度,δ1为一个很小的数,最终Rgi即为当前态势下可发射距离的最大值Rmax。最小可发射距离Rmin的搜索与Rmax类似,在命中目标时,令ai=ai-1,bi=Rgi-1,否则令ai=Rgi-1,bi=bi-1。
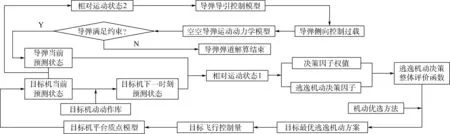
图5 基于目标逃逸机动预估的导弹追踪弹道解算逻辑Fig.5 Missile tracking trajectory calculation logic based on target escape maneuver estimation
当前可发射区间找到后,根据实际需求改变目标离轴发射角aasp_y及aasp_z,重新循环计算,直到导弹导引头可探测的角度搜索完毕为止。其中,当aasp_y与aasp_z同时改变时,解算结果为导弹三维可发射包络;保持当前aasp_z,改变aasp_y的情况下,解算结果为导弹的水平可发射区;同理,保持当前aasp_y,仅改变aasp_z的情况下,解算结果为导弹的垂直可发射区[16]。一般而言,水平可发射区可满足导弹的作战使用需求。
4.2 黄金分割搜索策略的简要改进办法
初始搜索距离a0、b0的取值对算法的搜索方向及边界的最终解算结果具有很大影响。由于初始搜索距离区间难以有效预估,存在2类情况,使算法的解算输出值可能为无效输出:
1) 第1类,存在可发射距离,但导弹始终无法命中初始位置位于黄金分割点处目标,可发射距离终值输出为0。
2) 第2类,可发射距离边界输出终值为初始搜索边界值。
为了解决上述2类问题,在文献[3]提出的黄金分割搜索算法的基础上,设置外层循环。首先对算法搜索输出结果进行评估,当边界输出值为零或等于搜索范围边界值时,执行外层循环。通过平移初始搜索点,对初始搜索范围进行动态修正,实现边界值的二次搜索。基于目标机动预估的远边界搜索流程如图6所示,图中,d为动态修正距离,s为最大修正次数。

图6 基于目标机动预估的可发射区远边界搜索流程Fig.6 Far-boundary search flowchart for launchable area based on target maneuver estimation
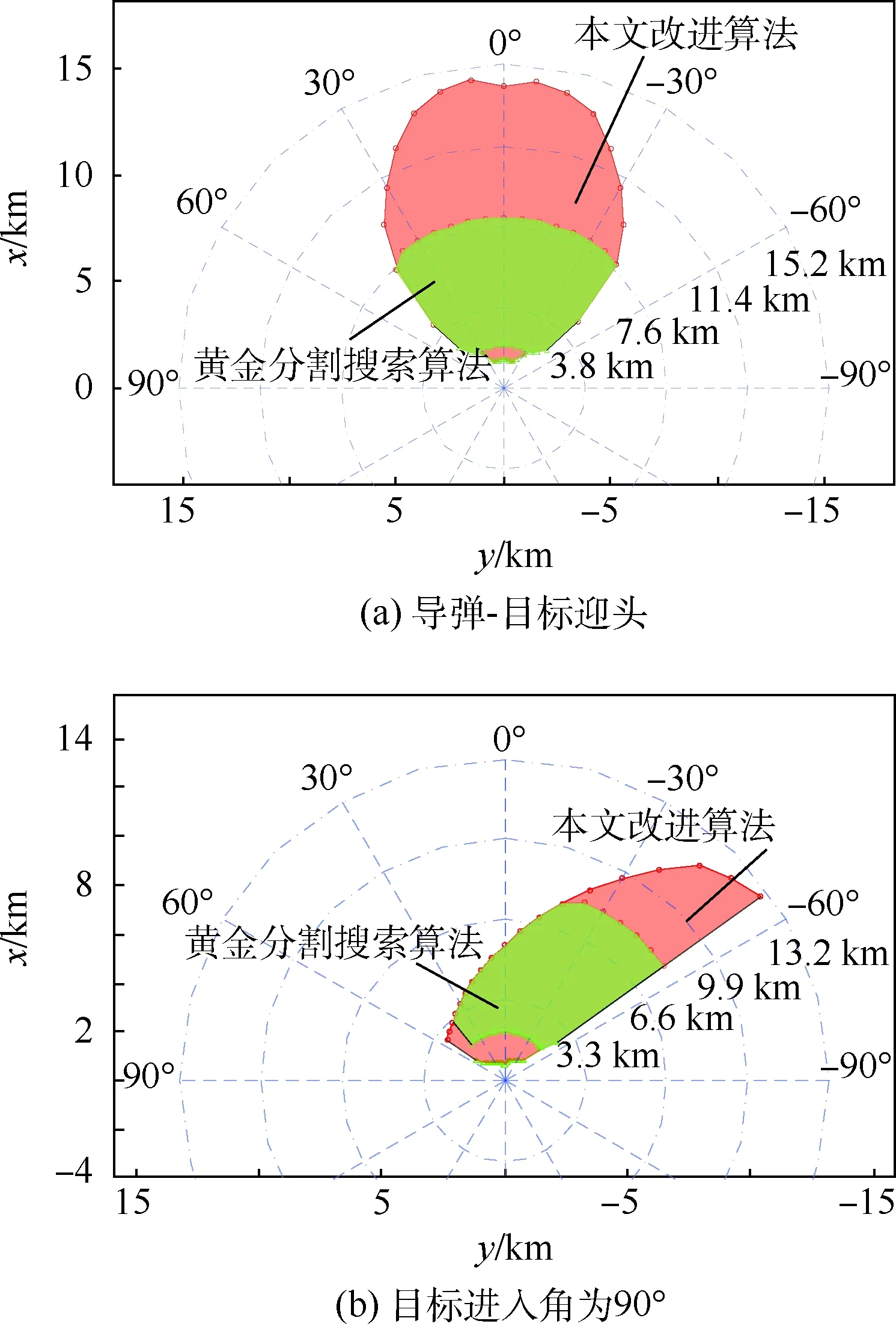
图7 不同解算方法在可发射区解算面积上的对比Fig.7 Comparison of calculated area of launchable area between different algorithms
通过动态修正初始搜索范围,在d取值合理的情况下,第2类问题很容易克服;对于第1类问题,通过边界值动态重复搜索,极大地降低了导弹误判不存在可发射距离的概率。当修正次数达到最大修正次数s时,若仍无非零值输出,则认为在该状态下,导弹不存在可发射距离。
为了检验本文提出的改进黄金分割搜素算法相对于传统的黄金分割搜索算法,在可发射区解算效果上的提高,设置对比仿真实验,为体现一般性,2种解算方法在对可发射区解算时,均使目标保持匀速直线状态。随机确定远近边界初始搜索空间[a0,b0],在相同初始状态,导弹与目标分别 构成相对迎头和目标水平进入角为90°的2种初始态势下,2种方法所解算的可发射区对比仿真结果如图7所示,可见,本文提出的改进黄金分割搜索算法在可发射区解算面积上有了明显提高,实现了发射初始值的动态修正,较好地解决了由于初始搜索空间难以选择而导致的可发射区边界无效输出的问题,从而实现了对可发射区边界的精确搜索。
上述简要改进办法,采取的是在无效输出的情况下,修正搜索区间,对边界值进行循环重复搜索办法,这在算法上易于实现。由于未改变原算法根本结构,在修正两类无效输出的同时,保留了原有经典算法的有效特性;由于只对无效输出的情况进行二次搜索,可发射区的整体解算时间上与原算法无太大差异,保证了解算的快速性。
5 模型验证与仿真分析
为了使本文所构建的模型及相关算法得以充分验证,仿真部分主要包括目标逃逸决策部分性能验证和导弹可发射范围仿真验证两部分内容。
选取某型导弹的气动参数和相关数据,导弹最大离轴发射角设置为60°,发射后最大动态视场角为70°;可控飞行时间为20 s,最大飞行时间为27 s;导弹脱靶量为7 m,近炸解除保险时间为1.8 s,最大可用过载为40;控制平面内导引系数K固定为3。攻击机位于水平坐标原点,速度为0.8Ma,高度8 km;航向角为0°。目标机初速度为0.8Ma,目标机所允许的操控量变化范围为ntz∈[0,8],ntx∈[-1.5,1.5],μt∈[-π,π]。
黄金分割搜索策略中,远边界初始搜索范围:a0=0 km,b0=25 km,动态修正距离d=5 km,最大修正次数s=10;近边界初始搜索范围:a0=0 km,b0=5 km,动态修正距离d=0.5 km,最大修正次数s=8,仿真步长为0.2 s。
5.1 目标逃逸决策部分性能验证
假定导弹发射时刻,目标机与攻击机构成侧向迎头的相对态势,其中,aasp_y=30°,aasp_z=0°,aoff_y=180°,aoff_z=0°,γm=0°。
初始相对距离分别为R0=5 km和R0=8 km的2组状态下,基于目标机动预估的导弹-目标的追逃机动仿真轨迹如图8所示。
由于初始状态,2组条件下相对角度关系一致,因而初始时刻,目标机均大致执行右转弯爬升的逃逸机动策略。R0=5 km时,目标机高度爬升至8.864 km,仿真时间为7.31 s时,导弹命中目标;作为比较,R0=8 km时,目标机执行右转弯爬升+小时段俯冲+左转弯爬升的机动策略,当仿真时间为17.23 s,目标机高度爬升至9.848 43 km时,导弹离轴发射角ϑm=70.02°,突破自身所允许的动态视场角限制,导弹脱靶,此时导弹与目标的相对距离为1.828 41 km。同等条件,目标保持原运动状态,执行定常直线飞行的情况下,导弹分别于6.48 s和11.41 s命中目标,可见目标执行预估逃逸机动制约了导弹的攻击性能;对比同样执行预估逃逸机动的2组导弹追踪结果可知,导弹是否命中目标需满足初始发射距离的限制。
图9给出了上述2组状态,目标分别执行预估机动和保持定常状态的情况下,逃逸机动决策整体评价函数随时间的变化曲线。由图可知,在目标执行预估机动的情况下,评价函数值在经历了短暂的下降后,整体保持了增大的趋势,说明目标所执行的逃逸机动决策是有效的;对比目标保持定常状态的情况,在执行预估机动的条件下,评价函数值有了明显提高,进一步说明执行逃逸机动决策使整体态势朝着更有利于目标逃逸或更不利于导弹追踪的趋势发展,说明本文所构建的机动预估系统对目标机动行为的预估是有效的。图 中函数存在短时间的下降趋势,这与导弹及目标的相对状态有关,具体作用机理,在此不做赘述。
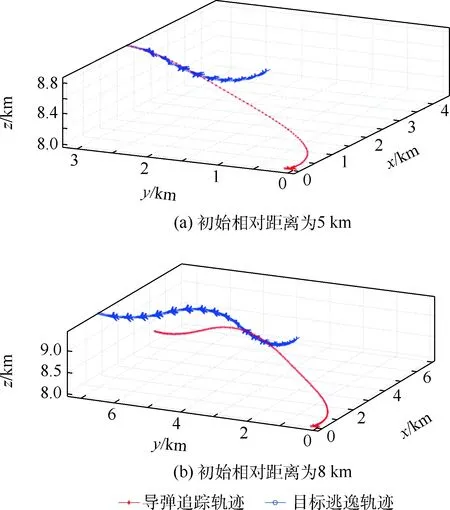
图8 侧向迎头条件下导弹-目标追逃机动仿真轨迹Fig.8 Simulated trajectories of missile-target pursuit- evasion maneuver under lateral head-on condition
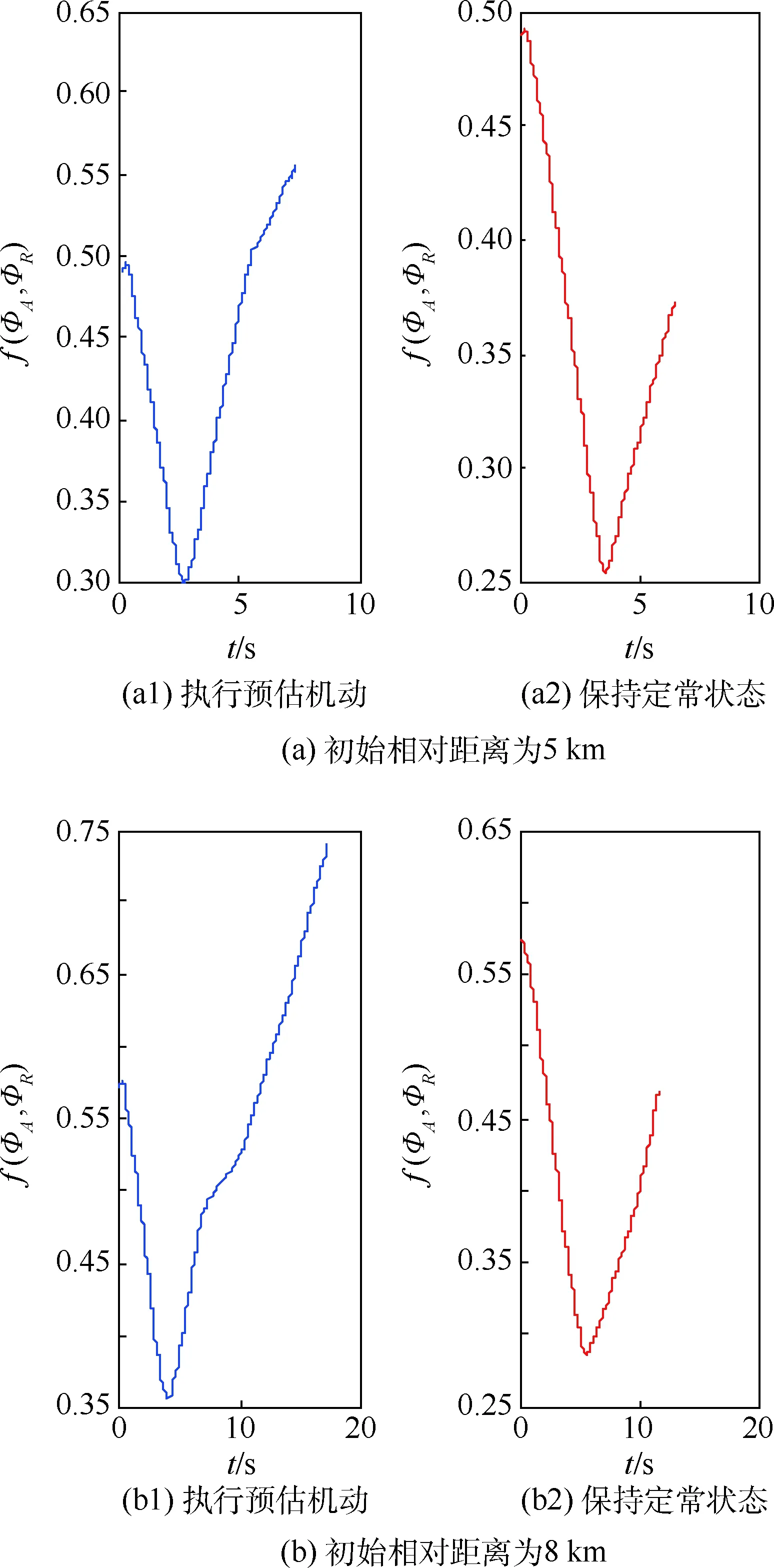
图9 侧向迎头条件下评价函数随 时间的变化曲线Fig.9 Curve of evaluation function over time under lateral head-on condition
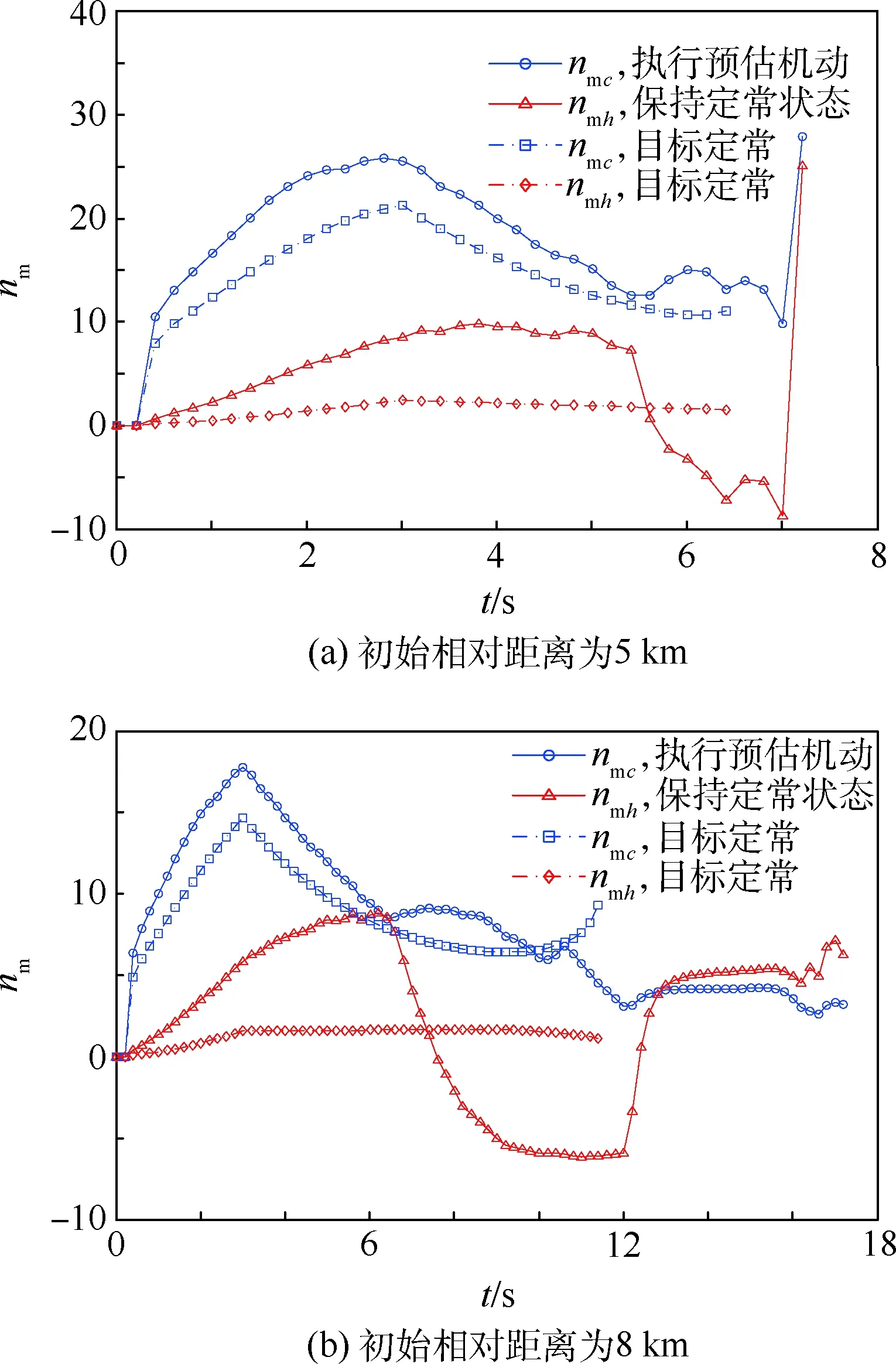
图10 不同运动状态情况下导弹侧向控制 过载函数随时间的变化曲线Fig.10 Curve of missile’s lateral control overload function over time under target’s different motion conditions
图10给出了不同状态下,导弹的侧向控制过载随时间的变化曲线。目标执行预估机动的情况下,导弹偏航和俯仰方向的侧向控制过载相较于目标保持定常状态的情况大幅度变化,且导弹需要更大的过载才能实现对目标的追踪,从侧面说明所构建的机动预估系统通过逃逸机动决策使整体态势朝着不利于导弹追踪的方向发展。
5.2 导弹可发射范围仿真验证
假定导弹发射后,目标可以获知导弹的方位信息,且忽略目标做出反应的时间延迟,机动预估系统根据目标与导弹之间的相对方位信息,输出目标预估飞行操控量,并假定目标执行预估机动。9种不同的初始相对态势下,基于黄金分割搜索策略的导弹可发射距离解算结果如表1所示,表中目标保持定常状态下的导弹可发射距离区间解算结果作为对照组。
由表1可知,目标执行预估机动的情况下,导弹的可发射距离的区间范围整体上小于目标保持定常状态的情况;其中,初始状态对应表中序号为2、3、4、7、9的情况下,基于目标执行机动预估的可发射距离区间内含于目标保持定常状态的情况;其余4种状态下,目标执行预估机动的情况下的最小可发射距离略小于保持定常状态下的最小可发射距离;整体来看,目标执行预估机动情况下的最大可发射距离值大大小于目标保持定常状态下的最大可发射距离值,进一步说明,目标执行预估机动有利于摆脱导弹追踪,这与前文的理论分析是一致的。
由于黄金分割搜索策略是一种粗步长的试探搜索策略,且同一相对态势下,随搜索距离的不同,目标机所采取的机动逃逸策略也存在差异,这些差异是否对可发射距离的判定结果产生影响,以及影响程度如何,仍然需要仿真实验进行验证。
设计蒙特卡罗仿真实验,在相对角度的可行域范围内,随机输入20组相对初始状态,输出可发射距离的解算区间。在可发射区间内自由取值,并保证每组初始状态下,各含有20组有效值。通过400次模拟打靶仿真,验证位于对应初始位置,且执行预估逃逸机动策略的目标,导弹是否具备攻击能力。在400次模拟仿真试验中,仅有9组情况下,导弹因离轴发射角限制未能最终命中目标,命中率为97.75%,说明黄金分割搜索策略对于本文提出的可发射距离解算问题具有较好的适应性,解算结果具有较高的置信水平。
为了检验本文所构建的基于目标机动预估的可发射区,对高对抗空战,尤其是无人作战条件下,目标机动信息不确定问题的适应能力,再次设计蒙特卡罗打靶仿真实验,并将目标保持定常状态的可发射区作为对照组,通过命中率验证,本文所提方法对导弹命中效果的提高。仿真中,导弹速度、高度及目标的初速度等信息与本节题设部分所述的仿真初始条件保持一致,目标在平台允许的范围内,以随机控制量实施任意机动,且控制量在决策周期内保持恒定。为了使对比效果更为显著,选取表1中2种表示形式下,可发射距离值差异最大的其中5组状态,状态1、3、5及7、8;每组状态下,在可发射距离解算区间内随机选取5个数值作为距离测试值;空空导弹对每一个距离测试值对应状态的目标进行10次模拟打靶测试,共计进行500次打靶仿真测试。由于2种形式的可发射区在对应状态的可发射距离区间上存在重叠,因而,在对照组测试距离选取时,主要选择与本文提出的可发射距离不重叠的区域。其中 2组状态下的导弹打靶测试的统计结果如表2所示,仿真中,导弹对本文提出的可发射距离区间内的机动目标整体命中概率为89.6 %,对照组可发射区间内的目标整体命中概率为37.6 %,在概率数值上高出52个百分点;在命中水平上,位于本文提出的发射区间内的目标相较于该区间之外的目标提高138.3 %,说明本文提出的可发射区更能适应空战中剧烈的态势变化,对不确定信息条件下的空战对抗过程具有更高的适应水平。
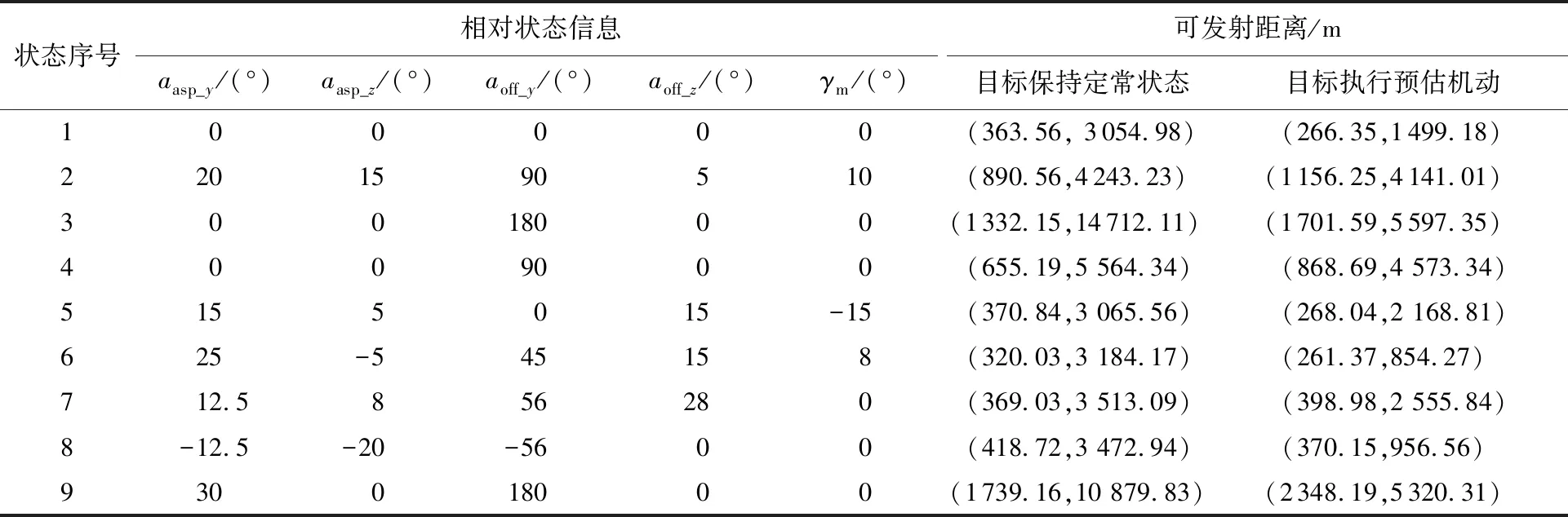
表1 不同运动状态下的导弹可发射距离解算结果
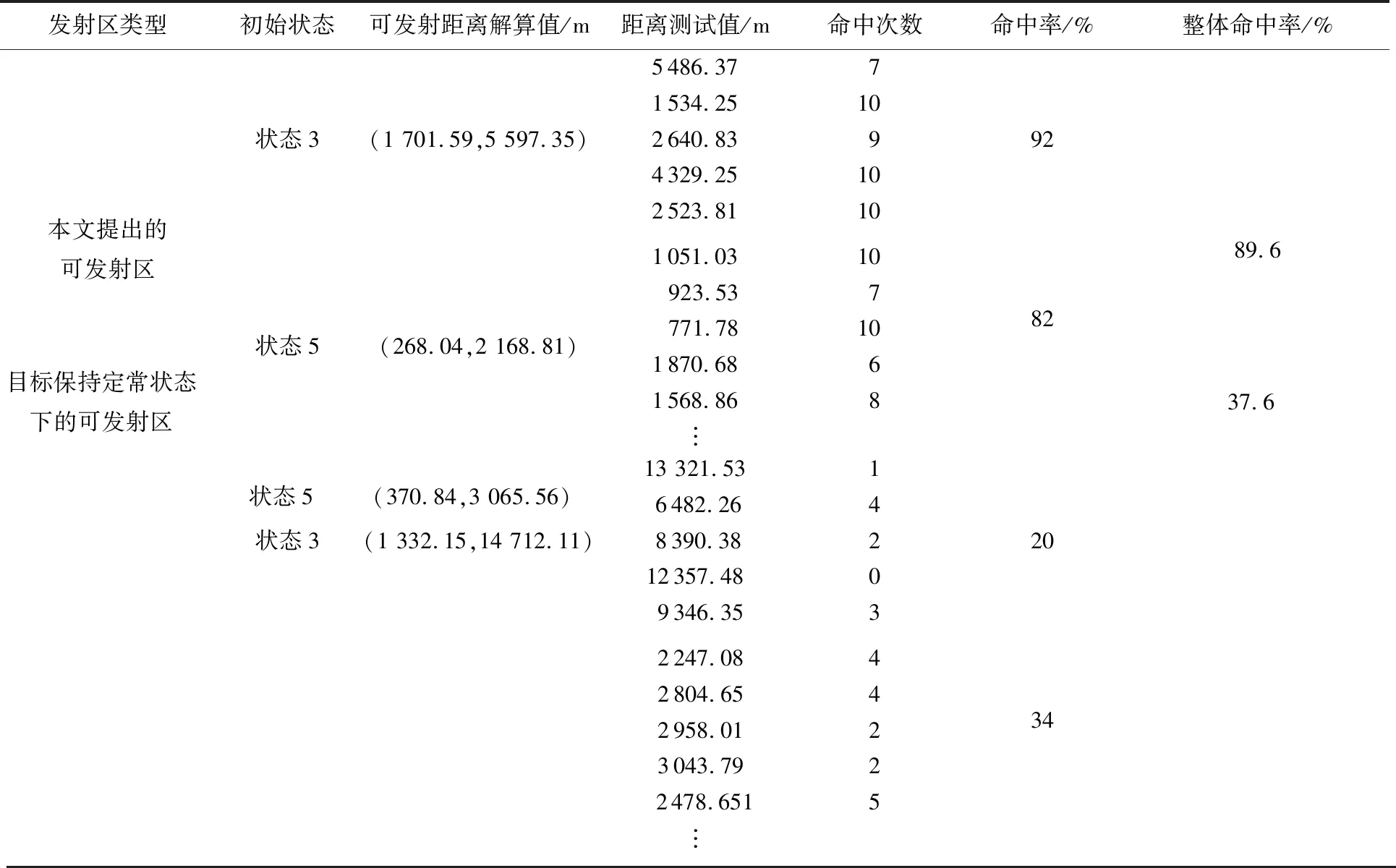
表2 导弹模拟打靶测试结果Table 2 Results of simulated missile target test
图11给出了目标进入角为90°和导弹-目标迎头2组典型态势下,空空导弹水平可发射区的整体解算结果,图中左侧部分为目标保持定常状态的静态可发射区,右侧部分为本文提出的基于目标逃逸机动预估的导弹可发射区;绿色三角部分代表可发射区的近边界,红色圆形部分代表可发射区的远边界,黑色连线部分为导弹可攻击临界值连线形成的侧边界,侧边界以外区域为导弹不可攻击的区域。由图可知,本文所提出可发射区,相较于传统的目标保持定常状态的静态可发射区,在可发射区域面积上有所减小,远边界向距离减小的内侧收缩,侧边界向离轴发射角减小的方向收缩,这主要是因为更大的距离使目标逃逸机动具备更大的时间裕度,有利于目标逃逸;而当离轴发射角增大时,导弹受动态视场角的影响程度也增大,从而不利于导弹的追踪,这与导弹应用实际是一致的。
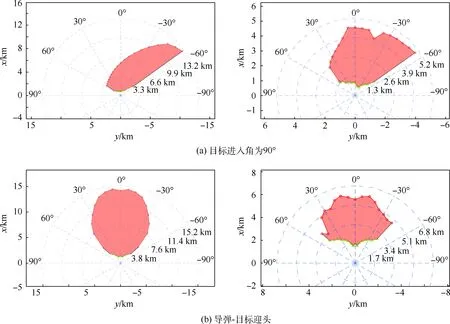
图11 典型情况下不同形式的2种可发射区对比解算结果Fig.11 Calculation result of two forms of launchable area under typical condition
6 结 论
本文面向无人自主空战的条件下对空空导弹火控解算的特殊需求,提出了基于目标机动预估的导弹可发射区问题。设计了基于目标追逃对抗策略的目标机动预估系统,将导弹发射后的目标运动过程抽象为一个动态追逃对抗的过程,根据预测的目标方位信息,利用黄金分割搜索策略实现对可发射区边界的快速精确搜索。仿真结果表明:
1) 基于目标机动预估的空空导弹可发射区在攻击面积上小于传统的目标保持定常状态的导弹可发射区。
2) 位于本文所提出的基于目标逃逸机动预估的可发射区内的目标,导弹具有更大的命中概率。
3) 基于目标机动预估的可发射区由于对导弹发射后的目标逃逸行为进行了预估,因而相较于传统的可发射区,更能适应现代空战中剧烈的态势变化,符合现代空战,尤其是无人自主空战条件下的应用实际。
