基于灰色理论模型预测上海市质量竞争力指数

(1.上海理工大学管理学院，上海,200093；2.上海理工大学光电信息与计算机工程学院，上海,200093)

1 引言

近几年中国越来越重视企业质量品牌的发展，习近平总书记在党的十九大报告中指出：“我国经济已由高速增长阶段转向高质量发展阶段.必须坚持质量第一、效益优先，以供给侧结构性改革为主线，推动经济发展质量变革、效率变革、动力变革.” 李克强总理在2017年《政府工作报告》中强调：“全面提升质量水平，广泛开展质量提升行动，加强全面质量管理，夯实质量技术基础，强化质量监督，健全优胜劣汰质量竞争机制[1].

当前中国制造业正面临从“速度”迈向“质量”的过渡与转型，而实现并促进制造业向“质量”转型要特别清晰地掌握“质量”这一转型要素的核心作用.质量竞争力反映的是以质量为核心要素而使竞争主体在市场中获得持续优势的能力，所以构建科学的制造业质量竞争力预测评定体系具有十分重要的理论指导意义和实践价值[2].除此之外，国外学者Kumar等[3]所提出的质量竞争力指数(Quality Competitiveness Index，QCI)模型也为衡量质量竞争力提供了一个强有力的标准.国内最具代表性的应用成果是原国家质检总局依据工作实际而研发的全国制造业质量竞争力指数，并依据此指标体系，每年发布各个地区的质量竞争力指数[4-5].

我国众多学者在制造业质量竞争力评价与预测方面做了许多研究：程红等[2]基于“钻石模型”构建了一套包括质量要素、质量需求、相关产业支持、行业结构与竞争、政府质量管理、城市发展机会六大维度的制造业质量竞争力测评指标体系；王主鑫等[6]采用莫兰指数和聚类算法对制造业质量竞争力指数进行分析，而后前者的基础上运用改进的灰色理论对其进行了预测；汪建等[7]通过对比回归分析模型和灰色预测模型法，对各国制造业综合质量发展趋势进行了预测，通过对比国内外制造业发展现状，预测我国制造业质量追赶发达国家所需时间.

上海市作为改革开放排头兵和创新发展先行者，2017年质量竞争力指数达到93.20[1]，连续九年排名全国第一.对上海制造业质量竞争力指数的预测，有助于推动其保持现有优势，提高经济增长的质量和稳定性；更有助于上海企业找到自身定位，有目的的打造具有高质量竞争力的品牌，走出国门、走向世界.

常用的预测模型有波特钻石模型[8]、回归分析法[7]和灰色系统理论[9-14].其中，灰色系统理论广泛用于“少数据”、“贫信息”不确定性系统的研究对象，主要通过对“部分”已知信息的生成、开发，提取有价值的信息，实现对系统运行行为、演化规律的正确描述和有效监控[11].越来越多的学者把灰色系统理论应用在各个学科领域的研究上[15-19]，使得灰色系统理论的蓬勃生机和广阔发展前景正日益广泛地为国际、国内各界所认识和重视.本文引用上海2008-2017年制造业质量竞争力指数的10个数据，对2018年制造业质量竞争力指数进行预测分析.属于“部分信息已知，部分信息未知”的“小样本”、“贫信息”的研究对象，使用一般预测方法得出的结果误差较大，准确度不高，因此，使用灰色预测模型进行分析预测较合适.

2 质量竞争力和质量竞争力指数

质量竞争力是竞争主体以卓越质量赢得优势的能力.质量竞争力的研究是对质量管理理论和竞争力理论两个学科进行比较研究，探索其共同的一般规律，并对它们相互交叉、渗透的边缘地带，如顾客、过程、绩效等进行研究.在21世纪我国质量竞争力理论的提出适应了全球经济发展和科技进步的趋势，是我国企业经营发展的客观产物.

质量竞争力指数是指质量因素在塑造核心竞争力过程中发挥的程度，它通过分析与质量密切相关的因素以建立评价指标体系，并运用适宜的指数化评价方法进行量化测评而得来，可以简明、直观地体现质量竞争力的水平和状态.质量竞争力指数包含“质量水平”和“发展能力”两个二级指标.“质量水平”是根据对标准与技术水平、质量管理水平、质量监督与检验水平等质量指标的测量，反映一个行业或地区质量发展的当前状况；“发展能力”是根据研发技术改造能力、核心技术能力和市场适应能力等与质量相关的科技投入与产出指标的测量来评价一个行业或地区的质量发展的持续能力.

依据上海市质量工作领导小组办公室和上海市质量技术监督局编写的《上海市质量状况白皮书(2018年)》[1]，得2018—2017年全国及上海制造业质量竞争力指数，如图1所示：

图1 2008—2017年全国及上海制造业质量竞争力指数

由图1可知在2017年上海市质量总体水平持续提升.产品质量方面，制造业质量竞争力指数为93.20，连续九年排名全国第一，持续保持较强的质量竞争能力.这归功于上海市质量工作领导小组及各区委、区政府的共同努力、众多行业组织、企事业单位和广大市民的积极参与.2018年1月17日上海市委、市政府坚持质量领先战略，发布《开展质量提升行动的实施方案》，在全市范围开展质量提升行动，质量提升再上新高度.因此对上海制造业质量竞争力指数的预测，有助于提高经济增长的质量和稳定性，便于市政府对上海市经济发展的监测；有助于政府宏观经济政策的制定，确定下一阶段经济发展战略决策；有助于上海制造业企业的自身定位，提高产品质量竞争力.

3 GM(1,1)预测模型的建立方法

3.1 GM(1,1)预测模型的建立

灰色系统理论是中国学者邓聚龙教授[13]在1982年创立的，把已知的参数称为白色参数，未知或不确定的参数称为黑色参数，系统中既有白色参数又有黑色参数就称为灰色系统.灰色系统理论以信息不完全系统的行为表现、行为内函、行为关系、行为环境的层次性、动态性、信息性、量化性等为主要目的[10]，可以广泛用于“少数据”、“贫信息”不确定性系统的研究对象，主要通过对“部分”已知信息的生成、开发，提取有价值的信息，实现对系统运行行为、演化规律的正确描述和有效监控.

灰色预测是基于灰色系统理论做出的定量预测，是灰色系统理论与技术的重要组成部分：将说明客观对象现在状态,和过去状态的各种时间序列的数据,按某种方式组合到一起形成一个白色数据(或加工后的数据群或称为模块).再将需要预侧的时间序列的数据群(因数据尚来得到,或不确知)当作灰色模块,然后寻找这两种数据群间的内在联系,发展规律,是计量未来学的研究内容[9].GM(1,1)模型是灰色预测中应用最广泛的模型，是基于累加生成的数列预测模型，它是由一个单变量的一节微分方程构成，GM(1,1)模型的突出特点是：建模过程简单，模型表达式简洁，便于求解，应用广泛.其建立的步骤为：

步骤1 ：x(0)(1)，x(0)(2)，…，x(0)(N)是所要预测的某项指标的原始数据.对原始数据作一次累加生成处理，即

得到一个新的数列.这个新的数列与原始数列相比，其随机性程度大大弱化，平稳性大大增加.

步骤2：将新数列的变化趋势近似地用微分方程描述：

其中，a,b为辨识参数，可通过最小二乘法拟合得到：

步骤3：构造数据矩阵.上式中YN为列向量，YN=[x(0)(2)，x(0)(3)，…，x(0)(N)]T，B为构造数据矩阵：

步骤4：求出预测模型.GM(1，1)微分方程的解为：

利用预测模型，预测生成序列为：

还原为观测值的预测序列(即预测的第N+1个数据)为：

3.2 模型的检验

模型合格与否要通过对模型的多种检验来判断.模型检验合格后，才能用模型进行预测.灰色模型检验采用残差检验、后验差检验以及关联检验等三种方法来检验.

(1)残差检验

残差检验是模型精度按点的检验，分为绝对误差检验和相对误差检验.通过可信度p0检验判断误差变动是否平稳，一般要求p0>80%.绝对误差的计算公式为：

可信度为：

(3.1)

(2)后验差检验

后验差检验是检验预测曲线与模型曲线在空间相对位置的重合程度，后验差比值越小，预测模型的预测精度就越高.模型的精度等级划分一般由p和c共同刻画.

原始数据离差：

(3.2)

残差离差：

(3.3)

后验差比值：

c=S2/S1.

(3.4)

小误差频率：

p={|x(0)(k)-e-(0)|≤0.6744S1}.

(3.5)

c，p两个指标把预测等级分为四等，参见表1[14].

表1 预测精度等级表

3)关联检验

关联度检验是对模型曲线与预测曲线的形状接近程度的检验.关联度越大，预测模型的预测精度就越高，一般认为R≥0.6，模型较为可靠.

计算关联系数：

从模型建立的步骤可以看出，GM(1,1)预测模型计算十分复杂，但是已经有很多学者和软件公司通过编程软件和办公软件计算该预测模型，使后来者可以避免繁琐的计算，轻松得到预测结果.比如陈树德[20]教授用Excel求解灰色系统问题；胡辉在基于MATLAB组件技术的基础上，以单变量灰色预测模型为例，设计开发出相应的组件，并在VB和excel环境中进行测试应用，实际效果良好.除此之外，各大软件公司如绿色先锋，也开发出专门用于灰色系统计算的软件，只需输入已知的数据，软件自动生成中间计算过程和计算结果，并给出模型的残差检验、相对误差、关联检验和后验差检验.

4 上海市质量竞争力指数预测

4.1 建立预测模型

根据《上海市质量状况白皮书(2018年)》中上海市2008年—2017年制造业企业质量竞争力(QCL)为原始数据，如表2所示：

表2 上海市2008年—2017年制造业企业质量竞争力(QCL)

用灰色理论计算工具的“GM(1,1)模型”，建立预测模型，得到以下结果：发展系数a=-0.005346,内生控制系数b=89.366881，则b/a=-16716.588290.

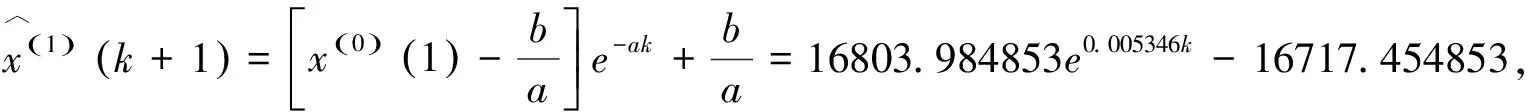
4.2 模型的检验

1)残差检验

灰色理论计算工具的计算结果给出了模拟值、残差、相对误差以及平均相对误差，如表3所示：

表3 原始数据、模拟值、残差、相对误差以及平均误差表

2)后验差检验

根据公式(3.2)～(3.5)，和表3.1预测精度等级表，得到后验差检验数据如下：

表4 后验差检验

其中后验差比值c<0.35，小误差频率>0.95，由此可得出所建模型的预测精度较好.

3)关联检验

表5 各年关联系数表

关联度R=0.7316，大于0.6，说明模型曲线和预测曲线具有较好的相似程度.

4.3 预测结果

由检验结果得出，所建模型后验差比值较小，小误差频率为1，模型的关联度大于0.6，因此模型的预测精度较高，可以用来预测2018年上海市制造业质量竞争力指数.

运用灰色系统理论建模软件，经过建立模型的步骤预测得到2018年上海市制造业质量竞争力指数约为94.51，远远高于上海市2008-2017年10年的质量竞争力指数平均值91.48，且达到十年来的最大值.从图1得到上海市10年来质量竞争力指数呈稳步上升的趋势，因此，如果上海市能在全市范围开展质量提升行动，坚持质量领先战略；鼓励企业抓住品牌质量的改革热潮，就有可能保持住当前的质量竞争力的优势，并且取得更高一步的发展，再创质量竞争力指数新高度.

如果需要预测2018年以后的数据，可以在每次预测后“新陈代谢”，剔除原始序列中最老的数据，将新的数据补充到数列中，使序列等维，接着再建立GM(1，1)模型，这样用预测灰数新陈代谢，逐个滚动预测，依次递补，直到完成预测目标[17].

5 结论

质量竞争力反映的是以质量为核心要素而使竞争主体在市场中获得持续优势的能力，所对上海市质量竞争力的预测能够为上海市下一阶段的质量发展方向，和战略制定提供参考.本文利用灰色系统理论对“少数据”、“贫信息”不确定性系统研究的优势，通过对“部分”已知质量竞争力指数信息，实现对“未知”质量竞争力指数的预测.即通过灰色理论系统对上海市2008-2017年质量竞争力指数的分析，预测2018年质量竞争力指数.而预测数值有助于上海市质量战略的制定，增强企业品牌质量的竞争力，进而提高经济增长的质量和稳定性.

通过分析可以看出，模型的可信度较高，后验差比值较小，小误差频率为1，模型的关联度大于0.6，预测模型通过了模型检验，模型拟合效果较好，并且发展系数a符合刘思峰、邓聚龙规定的模型适用范围.综上所述，用所建模型预测上海市2018年制造业的质量竞争力指数是可靠的.