New Inequalities for the Hadamard Product of Nonsingular M-matrices
2019-05-04ChenFubin
Chen Fubin
(Science Department,Oxbridge College,Kunming University of Science and Technology,Kunming 650106,China)
Abstract Some new inequalities for the minimum eigenvalue of nonsingular M-matrices are given. A numerical example is given to show that the new inequalities are better than some existing ones.
Key words M-matrix Hadamard product Lower bound Minimum eigenvalue
1 Introduction
The set of all real (complex) matrices is denoted byRn×n(Cn×n).Ndenotes the set {1,2,…,n} throughout.
If ann×nmatrixAsatisfiesA=λI-Bandλ≥ρ(B), whereBis a nonnegative matrix,λis a nonnegative real number andρ(B) is the spectral radius of matrixB,Iis an identity matrix, thenAis called anM-matrix. Furthermore, ifλ>ρ(B), thenAis called a nonsingularM-matrix, and is denoted asA∈Mn[1]; ifλ=ρ(B), thenAis called a singularM-matrix.
Our work is based on the following simple facts (see Problems 16,19 and 28 in Section 2.5 of [2] ):
(1)τ(A)∈σ(A),τ(A)= min {Re(λ):λ∈σ(A)} denotes the minimum eigenvalue ofA.
(2)τ(A)≥τ(B), whenA,B∈MnandA≥B.
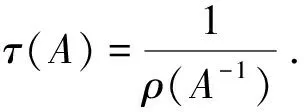
The Hadamard productA°BofAandBis defined asA°B=(aijbij). IfA,B∈Mn, thenB°A-1∈Mn[3].
A matrixAis irreducible if there does not exist any permutation matrixPsuch that
whereA11,A22are square matrices.
Given a matrixA=(aij)∈Rn×n, for anyi∈N, let
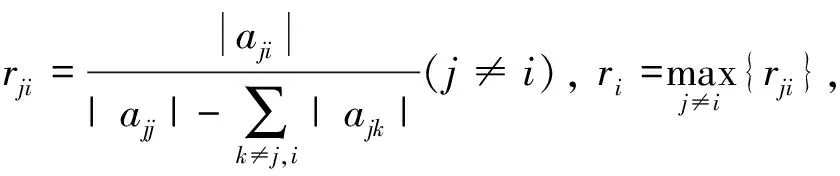
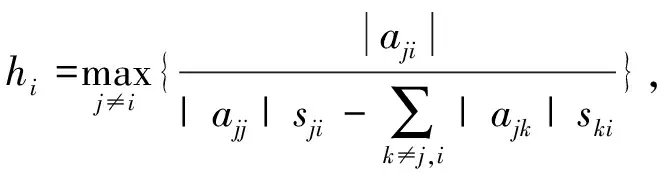
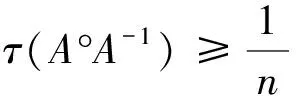
In [9], Li et al. gave the following result
Furthermore, ifa11=a22=…=ann, they have obtained
In [10], Li et al. gave the following sharper result
In this paper, our motives are to improve the lower bounds for the minimum eigenvalue ofM-matrices, which improve some existing results.
2 Main results
In this section, we give some lemmas that involve inequalities for the entries ofA-1. They will be useful in the following proofs.
Lemma 2.1[13]LetA,B∈Cn×nand suppose thatE,F∈Cn×nare diagonal matrices. Then
E(A°B)F=(EAF)°B=(EA)°(BF)=(AF)°(EB)=A°(EBF).
Lemma 2.2[14]LetA∈Mn, andD=diag(d1,d2,…,dn),(di>0,i=1,2,…,n). ThenD-1ADis a strictly row diagonally dominantM-matrix.
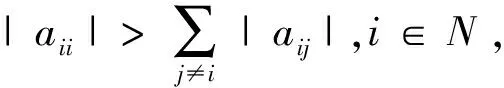
Lemma 2.4[15]IfA=(aij)∈Cn×n, then there existx1,x2,…,xn(xi>0) such that
Lemma 2.5[16]IfA-1is a doubly stochastic matrix, thenAe=e,ATe=e, wheree=(1,1,…,1)T.
Lemma 2.6[3]IfP∈Mnis irreducible, andPz≥kzfor a nonnegative nonzero vectorz, thenτ(P)≥k.
Theorem 2.1IfA=(aij)∈Mnwith strictly row diagonally dominant, thenA-1=(βij) satisfies
ProofThe proof is similar to the Theorem 2.1 in [9].
Theorem 2.2IfA=(aij)∈Mmwith strictly row diagonally dominant, thenA-1=(βij) satisfies
ProofLetB=A-1. SinceAis anM-matrix, soB≥0. ByAB=In, we have
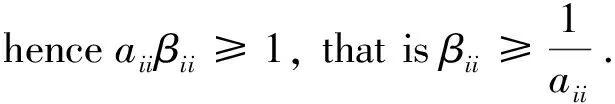
By Theorem 2.1, we have
i.e.,
Theorem 2.3LetA=(aij)∈Rn×nbe anM-matrix, and suppose thatA-1=(βij) is a doubly stochastic matrix. Then
ProofSinceA-1is a doubly stochastic andAis anM-matrix, we know thatAis strictly diagonally dominant by row. By Lemma 2.5, we have
and
Then, by Theorem 2.1, fori∈N
i.e.,
Theorem 2.4IfA=(aij),B=(bij)∈Mn, then
ProofBy Lemma 2.1, and Lemma 2.2, for convenience and without loss of generality, we assume thatAis a strictly diagonally dominant matrix by row.
First, we assume thatA,Bare irreducible. Letτ(B°A-1)=λandA-1=(βij), by Lemma 2.4 and Theorem 2.1, there exists anisuch that
i.e.,
By Theorem 2.2, we obtain
When one ofAandBis reducible.T=(tij) denotes the permutation matrix witht12=t23=…=tn-1,n=tn1=1, the remainingtijzero. We know thatA-εTandB-εTare irreducible nonsingularM-matrices withε>0[1]. we substituteA-εTandB-εTforAandB, the result also holds.
Corollary 2.1IfA=(aij),B=(bij)∈MnandA-1is a doubly stochastic matrix, then
Corollary 2.2IfA=(aij)∈MnandA-1is a doubly stochastic matrix, then
Theorem 2.5IfA=(aij)∈Mnis irreducible strictly row diagonally dominant, then
ProofSinceAis irreducible, thenA-1=(βij)>0, andA°A-1is again irreducible. Note that
τ(A°A-1)=τ((A°A-1)T)=τ(AT°(AT)-1).
Let
(AT°(AT)-1)e=(d1,d2,…,dn)T,
wheree=(1,1,…,1)T. Without loss of generality, we assume thatd1=mini{di}, by Theorem 2.1, we have
Therefore, by Lemma 2.6, we have
RemarkSinceA∈Mnis a strictly row diagonally dominant,so 0≤sji≤dj<1 , then
By the definition ofhi, we have
hence
By 0≤hi≤1, we havevji≤sjiandvi≤si.
Therefore, it is easy to obtain that
That is to say, the bound of Corollary 2.2 is sharper than Theorem 3.1 and the bound of Theorem 2.5 is sharper than Theorem of 3.5 in [9].
3 An example
Let
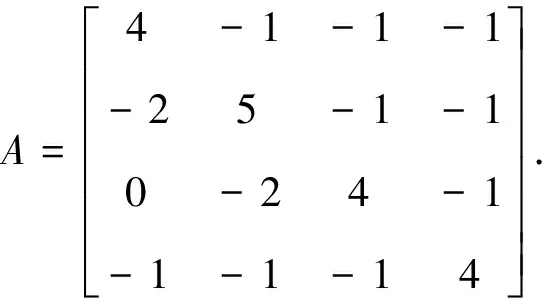
By Theorem 3.1 of [9], we have
By Theorem 3.2 of [10], we have
If we apply Corollary 2, we have
