结构平衡理论的时态模型：形式系统与程序实现

王轶 骆犀羚

1 引言

对由网络结构导致的社会网络随时间演变的特性进行逻辑分析是敌友逻辑（Logic of Allies and Enemies）（[10]）的主要目的。其理论基础来自于社会心理学家提出的结构平衡理论（[8,9]），而后又被推广为使用图论来进行刻画（[1,5,6]）。在该理论中，社会网络被处理为加标图：每个节点代表一个主体，每条边代表一个连带（tie）且标以积极或消极符号。积极符号通常用于标识朋友或盟友关系，而消极符号则用于敌人或对手关系。

如果网络结构满足特定的条件，那么这个网络是平衡的。举例来说，三个互为朋友的主体所表示的关系结构是平衡的，而三个互相敌对的主体所代表的关系结构被认为是不平衡的。经典文献（[1,5–7]）中通过图形中的回路来定义网络的结构平衡性。如果一条回路中有偶数条消极边，则该回路是积极的；反之如果有奇数条边，则整条回路是消极的。例如，图1表示具有五个主体（a,b,c,d,e）和三条回路（abc、abdec和bced）的网络。因为图中每条回路都有偶数个消极边，所以全部回路都是积极的。这种只有积极回路的网络就称为是平衡的。结构平衡理论认为，社会网络有向平衡网络演变的趋势，虽然这一过程可能需要很长时间，并且可能由于各方面因素的影响而无法真正达到平衡。

敌友逻辑引入了一个与结构平衡秉承相似直观但有所不同的概念，称为稳定性。在敌友逻辑中，如果一对主体更愿意保持彼此现有的关系，那么他们当下的关系是稳定的。如果网络中每对主体间的关系都是稳定的，那么整个网络就是稳定的。更细致地说，如果两个主体是朋友，并且他们的共识（即共同的朋友或敌人）多于分歧（即与其一为友而与另一为敌的那些主体），则两者的关系是稳定的。如果两个主体是敌人，并且分歧多于共识，该关系也是稳定的。此外，对于非敌非友的两个主体，如果共识与分歧数量相等，则也具有稳定关系。其他情况则是不稳定的。

稳定性概念乍看起来或许与平衡性相去甚远，但它采用的观点实际上源自结构平衡理论最初的想法（[8,9]）：对第三者抱有相似态度的一对个体倾向于彼此喜欢，对第三者抱有不同态度的一对个体倾向于彼此厌恶。

文中将引入敌友逻辑的公理系统，它在分支时间逻辑CTL（[3]）的公理系统之上增加一些与网络相关的公理和规则。该系统的可靠性和完全性也将得到证明。

敌友逻辑的模型检测、有效性以及可满足性检测问题都是PSPACE完全的（[10]），其具体算法已通过Python程序实现，后文将具体说明其主要功能，包括如下常用函数：

•staScore()：对于给定的网络，计算其稳定性评分

•isStable()：判断给定网络是否稳定

•succNum()：对于给定的网络，计算其后继数目

•successors()：返回存储给定网络所有后继的列表

•isSucc()：判断一网络是否为另一网络的后继

•mc()：对于给定的网络和给定的公式，判断该网络是否满足该公式

•sat()和valid()：对于给定的公式，分别判断该公式是否可满足或是否有效

•satFind()：基于给定情况，找到满足给定公式的网络

文章结构如下。第2节介绍敌友逻辑（[10]）的语法和语义。第3节引入敌友逻辑的公理化，并证明其可靠性和完全性。第4节介绍敌友逻辑模型检测、有效性检测和可满足性检测的程序实现；其中第4.1和4.2节分别涵盖语义（网络相关）和语法（句法检查）的程序实现，而对模型、有效性和可满足性检测程序的说明则在第4.3节。文章最后一节总结并讨论后续工作。程序代码、例子和后期更新将通过如下网站维护：http://www.xixilogic.org/projects/lae。

2 敌友逻辑

本节简要介绍敌友逻辑（[10]）的语法、语义及其模型检测等问题。以自然数表示主体，ω表示所有主体的集合。当自然数n用于表示网络的个体与或者语言的参数时，它代表一个自然数的集合（即集合{0,1,...,n−1}）。这种处理方式与公理集合论中对自然数的常见定义保持一致（不妨参考[11]）。

2.1 网络与稳定性

n节点网络是具有n个节点的带三个符号的有穷无向完全图。准确地讲，一个n节点网络是一个有序对(n,E)，使得：

•n={0,...,n−1}是有穷的主体集；

•E:{{i,j}|i,j∈n}→{1,0,−1}是一个全函数，用于表示每对主体之间的

积极(+)、消极(−)或中立(0)连带，并且满足E({i,i})=0。

这里不考虑自反圈（例如i是自己的朋友或敌人）或两个主体之间具有多重关系（例如i和j既是朋友又是敌人）等情形。在不引起混淆的情况下，通常以ij或ji表示边{i,j}。有时也以E(ij)或E(ji)（或者E(i,j)或E(j,i)）表示E({i,j})。

在敌友逻辑中，两个主体之间的共识或吸引力定义为使他们建立或保持朋友关系的理由数，即他们的共同朋友或敌人的总数。类似的，两个主体间的分歧或排斥力是使他们建立或保持敌对关系理由数，即与其一为友但与另一主体为敌的主体的总数。准确说来，令N=(n,E)为一网络且i,j∈n，则ij之间的共识（记为attr(ij)）和分歧（记为rep(ij)）满足：

两主体间关系的稳定性取决于他们现有的关系和彼此间的共识与分歧。如果i和j是朋友（即E(ij)=1），且他们之间的共识不小于分歧，则他们的关系是稳定的。类似地，如果i和j是敌人，且彼此间分歧不小于共识，则也是稳定的。而中立关系只有当吸引力等于排斥力时才是稳定的。除此以外的情况都是不稳定的。ij连带的稳定性评分以score(ij)表示，定义如下：

不难发现，如果score(ij)≥0，那么ij连带是稳定的。反之，则不稳定。

如果网络中所有的边都稳定，则称该网络稳定。反之则不稳定。一个网络的稳定性评分是其中所有边的稳定性评分之和。

称网络N2=(n,E1)是网络N1=(n,E2)的后继（记为N1⇝N2），如果满足如下条件之一：

•当N1稳定时：N1=N2,

•当N1不稳定时：N1与N2仅在一条边ij的符号上有差别，同时满足：要么在N1中有attr(ij)>rep(ij)且E2(ij)=1，要么在N1中有rep(ij)>attr(ij)且E2(ij)=−1。

网络集上的后继关系形成了一个树形结构，其每条分支代表网络随时间演进的过程，仅有的循环出现于稳定网络到自身的回路。关于上述定义和结论的更多解释详见（[10]）。这里值得强调的是，网络的演进过程中稳定性评分并不一定递增。虽然在多数情况下，后继网络的稳定性评分确实高于其前驱，并且这确实反映了网络结构趋于平衡的性质，但并不能排除稳定性评分走低的临时情况。

2.2 语言和语义

这里引入有穷版本的LAE，即可用主体集为某个自然数n={0,1,...,n−1}，记为LAEn。参数n可以是任意大于等于3的自然数（当n<3时网络平衡概念失去意义，因此不予考虑）。LAEn的语言Ln的语法定义如下：

其中i∈n。原子命题P(i,j)、N(i,j)和O(i,j)将分别用于表示ij边是积极、消极和中立的，而stb和bal将分别表示网络是稳定和平衡的。符号T、∼、/、/、->和<−>是命题联结词（正文中使用中缀形式∧、∨、→和↔分别表示后四个符号以方便阅读）。其他算子来自CTL（[2,3]）。

Ln通过大小为n的网络的集合加以解释。任意N=(n,E)是否满足（记作|=）某个Ln公式可归纳定义如下（其中φ,ψ∈Ln且i,j∈n）：

语句“ij边稳定”（记为stb(i,j)）可以在Ln中表达如下：

因此不必作为原子语句引入。

由上述语义可以得到一系列逻辑LAEn(n∈N且n≥3)，通常以LAE表示任意这样的逻辑。如下定义引自（[10]）：

定理1(LAE的计算复杂性).LAE的模型检测与有效性检测问题都是PSPACE完全的。

3 公理系统

由定理1，敌友逻辑LAE的有效性检测问题是可判定的，因此是可公理化的：至少可以穷举所有有效式。但这并不意味着可以得到一个契合语法证明直观的公理系统。本节给出LAE的公理系统，并证明其可靠性和完全性。

下文将给出逻辑LAEn的公理系统LAEn，其中引入了描述这一概念。描述（将以δ表示）是形如∧i,j∈npi,j的公式，其中pi,j是原子命题P(i,j)、N(i,j)或O(i,j)。描述将用于刻画网络，而最好的方式是使同一网络被唯一的描述所刻画。为实现这一目的，需要增加一些限制条件。

首先约定描述中的边按照特定顺序排列，例如规定p1,2永远出现在p1,3的左边，这样可以避免出现对同一网络的逻辑等值的不同描述。令N=(n,E)为一网络，N的描述，记为δ(N)，是满足如下要求的合取式∧i,j∈npi,j（合取项有确定的顺序）：

在上述限制条件下，不难证明δ(N)是存在且唯一的。此外，并非所有的描述都是某个网络的描述（例如出现合取支P(1,1)，或同时出现P(1,2)和N(2,1)等情况），但如果δ是N的描述，即δ=δ(N)，则称δ描述了N。不难证明，δ(N)描述了唯一一个网络，即N。

稳定公理（记为SF）是如下公式：

其中δ1,...,δm枚举了所有稳定网络的描述。类似地，平衡公理（记为BF）是如下公式：

其中，δ1,...,δm枚举了所有平衡网络的描述。

令δ描述网络N，则δ的明日公理（记为tf(δ)）是如下公式:

其中，δ1,...,δm是δ所描述的网络的所有后继的描述。明日公理tf(δ)可以简写为δ→∇{δ1,...,δm}，其中的∇有时称为覆盖模态词（cover modality）。明日公理的数量是有穷的。

逻辑LAEn的公理系统LAEn如图2所示。LAEn由CTL的公理和规则（[4]）、用于刻画网络以及网络更新的公理和规则以及一些CTL时态算子的定义公理组成。{AX,AU,EU}是CTL时态算子的一个完全集，因此其他算子EX、AG、EG、AF和EF都是可定义的，这些定义公理都放在“CTL模态词定义”栏目下。此外，CTL公理DX可由明日公理推导出，因此可以删去。

不难验证LAEn的可靠性：所有公理都有效并且所有规则都保持有效性。其具体证明不再赘述。这里主要关注LAEn的完全性。下面的结论适用于任意数量的主体（即任意n∈ω且n≥3），因此以Φ⊢φ表示公式φ是以公式集Φ为前提在系统LAEn中可推演的（⊢φ即表示φ是LAEn的定理）。

引理1.假设⊢δ→∇{δ1,...,δm}，则如下结论成立：

1.如果对所有i=1,...,m都有⊢δi→φ，则⊢δ→AXφ

2.如果存在i=1,...,m使得⊢δi→∼φ，则⊢δ→∼AXφ

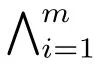
引理2.对任意网络的描述δ和任意公式φ，要么⊢δ→φ，要么⊢δ→∼φ。

证明.网络的描述中的两个不同合取支不能同时为集合{P(i,j),N(i,j),O(i,j)}中的元素。这由公理(PN)和(Neut)保证。此外，P(i,j)和P(j,i)（对于N和O也类似）要么同为网络描述的两个合取支，要么都不是，这由公理(Symm)和(Neut)保证。因此，网络描述的一致性可以通过命题逻辑和这些公理得到。因此⊢δ→φ和⊢δ→∼φ不能同时成立。

下面通过对φ做结构归纳来证明⊢δ→φ与⊢δ→∼φ中至少有一个成立。

•φ是原子公式P(i,j)。如果P(i,j)是δ的一个合取支，那么⊢δ→P(i,j)。否则N(i,j)和O(i,j)之一是δ的合取支。因此，要么⊢δ→N(i,j)，要么⊢δ→O(i,j)。又因为⊢N(i,j)→ ∼P(i,j)（根据PN）且⊢O(i,j)→ ∼P(i,j)（根据Neut），故有 ⊢ δ→ ∼P(i,j)。

•φ为N(i,j)和O(i,j)的情形可作类似证明。

•φ=∼ψ：若⊬δ→∼ψ，由归纳假设知⊢δ→ψ，故⊢δ→∼∼ψ。

•φ=(ψ → χ)：若 ⊬δ→ (ψ → χ)，则⊬δ→ ∼ψ且 ⊬δ→ χ。因此，⊬δ→(∼ψ∨χ)，即⊬δ→(ψ →χ)。

•其他命题联结词情形可类似证明。

•φ为stb的情形。假设⊬δ→stb。在此情况下δ不可能描述稳定网络。否则根据稳定性公理，⊢ stb ↔ (δ1∨···∨δm)（其中δ1,...,δm是所有稳定网络的描述）。如果δ描述稳定网络，那么δ是某个δi（i=1,...,m）。于是⊢ δ→ (δ1∨···∨δm)，并因此⊢δ→stb，与假设矛盾。所以δ描述的不是稳定网络，并且δ与所有的δi都至少有一个合取支是不同的。由此可知，⊢δ→∼(δ1∨···∨δm)。否则存在i=1,...,m使得⊢δ→δi，矛盾。根据稳定性公理，⊢δ→∼stb。

•φ为AXψ的情形。假设⊬δ→AXψ。由明日公理，有⊢δ→∇{δ1,...,δm}（其中δ1,...,δm是δ所描述网络的所有后继的描述）。在根据引理1(1)，存在i=1,...,m使得⊬δi→ψ。由归纳假设知⊢δi→∼ψ。故由引理1(2)，⊢δ→∼AXψ。

•φ为AU(ψ,χ)的情形。假设⊬δ→ AU(ψ,χ)。通过(AU)进行等值替换，有⊬δ→ (χ∨(ψ∧AXAU(ψ,χ)))。由此可知，(1)⊬δ→ χ且[(2)⊬δ→ ψ或(3)⊬δ→AXAU(ψ,χ)]。当(1)和(2)同时成立时，根据归纳假设，有⊢δ→∼χ和 ⊢ δ→ ∼ψ。由此可知 ⊢ δ→ ∼(χ∨(ψ∧AXAU(ψ,χ)))。再由 (AU)，有⊢δ→ ∼AU(ψ,χ)。当(1)和(3)同时成立时，由(3)和引理1(1)知，明日公理δ→ ∇{δ1,...,δm}中存在δi(1 ≤ i≤ m)使得⊬ δi→ AU(ψ,χ)。这就得到与开头假设部分相似的情形，但是建立在δ的后继δi之上。继续这个过程有穷多次（明日公理有穷）直到得到⊬δs→AU(ψ,χ)，其中δs描述稳定网络（即⊢δs→stb）。由此可得 ⊬ δs→ (χ ∨ (ψ ∧ AXAU(ψ,χ)))，同理亦可得 (1′)⊬ δs→ χ 且 [(2′)⊬ δs→ ψ 或 (3′)⊬ δs→ AXAU(ψ,χ)]。对于 (1′)和 (2′)同时成立的情形，仍有⊢δs→∼χ且⊢δs→∼ψ，并且⊢δs→∼AU(ψ,χ)成立。通过反复使用(AU)进行等价替换，可得⊢ δ→ ∼AU(ψ,χ)。当(1′)和(3′)同时成立时，因为δs→ ∇δs是明日公理，根据(1’)和(Tm1)，有⊢δs→∼AU(ψ,χ)。反复使用引理1(2)并使用(AU)进行等价替换，可以得到⊢δ→∼AU(ψ,χ)。

•φ=EU(ψ,χ)的情况与AU(ψ,χ)类似，使用公理(Tm2)替代(Tm1)即可。

根据“CTL模态词定义”类型中的公理，包含其他时态算子的公式可归约为不含这些算子的公式，从而结论对所有公式成立。

引理3.任给极大一致的公式集Φ，描述δ和公式φ。如果δ,φ∈Φ，则⊢δ→φ。证明.使用反证法，假设δ,φ∈Φ且⊬δ→φ。由引理2知⊢δ→∼φ。根据Φ的极大性，有∼φ∈Φ，从而Φ不一致。矛盾！

任给极大一致的Ln公式集Φ，以NΦ表示网络(n,E)，其中E满足：

可以证明NΦ存在且唯一。

引理4.令Φ为极大一致的公式集，且δ是网络的描述。则如下命题等价：

1.NΦ|=δ 2.δ描述NΦ3.δ∈Φ

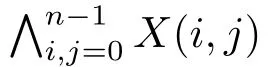
引理5.令Φ为极大一致的公式集，则NΦ|=Φ。

证明.假设δ描述NΦ。由引理4可得NΦ|=δ和δ∈Φ。对任意φ∈Φ，由引理3，有⊢δ→φ。再由LAEn的可靠性知|=δ→φ，故NΦ|=φ。因此NΦ|=Φ。

与CTL只有弱完全性不同，LAEn具有强完全性。这主要是因为在LAEn中所有的时间线都是有穷的（每个网络都能在有限步到达稳定，且稳定网络不再发生变化）。

定理2(强完全性).任给极大一致的公式集Φ和公式φ，如果Φ|=φ，则Φ⊢φ。

4 程序实现

本节介绍基于Python的LAE模型和有效性检测程序，主要分为网络的实现（语义角度）、语法检测（语形角度）和模型检测等的实现（语义和语形交叉）三个部分。

4.1 网络的实现

在程序实现中，n节点网络（n∈ω）是二元组(n,E)，其中E:n×n→{−1,0,1}满足E(i,j)=E(j,i)，且对所有i,j∈n都有E(i,i)=0。该定义与第2节中的差别在于这里的每个主体对都是有序的，但因为保证了对称性，两个定义是共通的。

n节点网络可以看成是n×n矩阵，其中每个元素(i,j)代表主体i与j之间的连带。左下图矩阵表示一个6节点网络，对应于右下图所示网络。

如前所述，网络示意图中的实线表示积极连带，虚线表示消极连带，而中性连带则不画线。该表示法与经典文献（[1]）中一致。

4.1.1 生成和表示

对于程序实现而言，网络其实就是前面定义的矩阵。但程序同时支持通过指定网络中的积极和消极连带来生成网络。

netInit()与netGen()这两个函数用于生成网络。函数netInit(n)初始化一个所有的边都是中性连带的n节点网络，即大小为n×n、元素全为0的矩阵。函数netGen(net,sign,*edges)可以通过为列表*edges中的边规定符号sign来修改网络net。

例如，以下几行代码生成上面图形中给出的6节点网络，该网络命名为net1（可使用命令print(net1)进行查看）。

函数netSize()返回所输入网络的大小。如果对上面定义的网络net1执行命令netSize(net1)，则返回值为6。

4.1.2 评分计算

对于给定的网络，边(i,j)的共识、分歧和稳定性评分分别由函数attr()、rep()和score()给出：

•attr(net,i,j)：返回网络net中边(i,j)的共识；

•rep(net,i,j)：返回网络net中边(i,j)的分歧；

•score(net,i,j)：返回网络net中边(i,j)的稳定性评分。

如果省略参数i与j，则输出结果为一个矩阵，其右上部每个位置的值都为对应边的相应值。例如，attr(4net)（其中，4net是一个4节点网络）的结果如下：

需要注意的是，对于在自循环ii，共识为包含i的全部连带的数量，而分歧为0。这些特殊情况目前在程序中并考虑，但不会导致后续检测结论出现错误。

用第4.1.1节中的例子，执行print(attr(net1))、print(rep(net1))和print(score(net1))命令将分别得到如下矩阵：

网络的稳定性评分被定义为其所有边稳定性评分的总和。函数staScore()（勿与score()混淆）可用于获得网络的稳定性评分。例如，命令staScore(net1)返回4。

4.1.3 后继

函数isStable()用于检测一个网络是否稳定。函数succNum()返回给定网络所有不同后继的数量。采用第4.1.1和4.1.2节中的例子，succNum(net1)返回2，即网络net1有两个后继。

函数successors()返回给定网络的所有后继网络的列表。例如，执行命令successors(net1)将输出如下结果（其中两个矩阵分别表示net1的两个后继）：

函数isSucc()可用来检测一个网络是否是另一网络的后继。如果存在时间线N0⇝ N1⇝ ···⇝ Nn使得N=N0且N′=Nn，则称网络N′是N 的n步后继。执行命令isSucc(net1,net2,num)，如果net2是net1的num步后继，则返回True，否则返回False。

定义如下网络：

然后使用检测它们中的某些是否为否另外一些的后继：

得到的结果分别为True、True、True、True、True和False。

4.2 语法检测

函数formChk(n,string)检验一个字符串是否为Ln的公式，即满足语法规则且只包含0到n−1主体的字符串。如果满足，则返回值为True。若否，则为False。此外，这个功能也被用在装饰器argsChk()中，该装饰器可保证其他函数输入的公式始终符合标准。

例如，运行以下代码得到的输出

返回的值分别为True、True、False以及False。

4.3 模型检测、有效性检测和可满足性检测的实现

模型检测、有效性检测和可满足性检测分别以函数mc()、sat()和valid()加以实现。下面给出具体说明。

任给网络N（由net表示）和公式φ（由formula表示），如果N|=φ，则命令mc(net,formula)返回True，否则返回False。

为方便输入网络，提供了函数desc()用以生成网络的描述（描述的定义见第3节）。实际输出的是部分的网络描述（矩阵），即仅仅是矩阵对角线右上方的那些连带。这样做并不会丢失信息，因为对于网络这样的无向而言，对角线两边完全对称。例如，print(desc(net1))输出如下：

/(N(0,1),/(O(0,2),/(O(0,3),/(N(0,4),/(N(0,5),/(P(1,2),

/(O(1,3),/(P(1,4),/(N(1,5),/(O(2,3),/(P(2,4),/(N(2,5),

/(O(3,4),/(O(3,5),N(4,5)))))))))))))))

上面使用的是前缀表达式，改用中缀表示并去除多余括号，即如下公式：不难验证，desc(net1)在且只在网络net1中为真。

任给公式φ，命令sat(n,φ)返回True，如果φ是n可满足的，即存在n节点网络N使得N|=φ；否则返回False。命令valid(n,φ)返回True，如果φ是n有效的，即所有n节点网络N都满足N|=φ；否则返回False。

目前还未对可满足性和有效性检测工具进行算法优化，只是通过测试所有网络将两类检测问题归约为模型检测问题，因此大型网络的结果输出可能会比较慢。

函数 satFind(n,formula,mode='normal')在默认情况（'normal'模式）下，会查找满足给定Ln公式的所有网络（可能非常耗时）。如果找不到，则返回False。如果设置mode='min'，则输出满足给定公式的最小网络（如果不可满足则返回False）。例如，print(satFind(5,'AXP(1,2)',True))的输出如右图所示。

5 结语

本文给出了敌友逻辑（[10]）的公理系统和程序实现。公理系统包含稳定公理（SF）和明日公理（TF）以及依赖网络描述的规则Tm1和Tm2。这些公理和规则是纯语形的，但很大程度上复制了网络更新的形式语义定义。我们不确定是否可以在不使用网络描述的前提下对敌友逻辑进行公理化，但我们给出的公理系统绝非毫无意义。它是对CTL公理系统的保守扩充，至少表明CTL的公理和规则对于本文引入的基于网络的形式语义仍然是有效的。

目前的程序实现严格地依照语义定义来进行。这也就意味着程序可以进行优化。例如，如果遇到形如AU(φ,ψ)∨∼AU(φ,ψ)这种可以通过命题逻辑简单判定的公式，程序中仍然需要（两次）检测AU(φ,ψ)是否为真。又如，可满足性检测的程序算法是从最小的网络逐一开始检测直到找到满足的网络，但通常来说，还有更好的策略去找到满足条件的网络。优化模型检测算法的方法有很多，这是从事定理证明等相关领域研究者经常面临的任务。本文的重点是给出行之有效的程序实现，而进一步的优化则是未来的工作方向。

网络中边的符号目前仅允许{−1,0,1}中的，对此进行推广是一件自然而然的事情。如果将符号的数字理解为概率，那么恰当的符号范围可能是常用于表示概率的实数区间[−1,1]。在这种情况下，一对主体的概率或许可以视为其共识或分歧符号的乘积。如果将符号理解为关系的强度，则使用自然数、有理数或实数都是可行的。关系的强度可以是共识或分歧中的最小值，或是它们的和。在结构平衡理论中增加关系强度的刻画早在（[12]）中就已经出现，这些将留作未来的任务。

使用图形表示网络可以使模型检测工具更加实用，我们打算在未来加以实现。除此以外，敌友逻辑适用于不同领域的版本也具有研究价值，我们将探讨允许网络更新算子、与博弈论结合等研究思路。