多智能体模态逻辑系统Kn中的知识遗忘
2019-05-04文习明方良达余泉常亮王驹
文习明 方良达 余泉 常亮 王驹
随着深度学习等一系列机器学习算法的不断完善,计算机逐渐具备了学习知识的能力。对于人类来说,除了具备不断学习知识的能力,还具备策略性遗忘知识的能力。遗忘不仅仅意味着记忆的遗失,也是一个帮助大脑吸收新知识并有效做出决策的积极过程。如何让计算机像人一样具备遗忘的能力,目前仍然是人工智能所面临的最大挑战之一。遗忘在基于符号逻辑的知识表示与推理(KR:Knowledge representation and reasoning)领域和基于统计的机器学习领域都有研究。特别是在KR领域,遗忘扮演着非常重要的角色。
在KR领域,遗忘(forgetting)的思想最早可以追溯到1854年Boole提出的“消去(elimination)”([4])。其直观含义是:从当前理论中删除某些信息,得到一个比原理论更弱的新理论,但在保留下来的信息范围内,新理论和原理论能够推导出一致的逻辑结论。在命题逻辑,一阶谓词逻辑、模态逻辑、描述逻辑、回答集逻辑程序设计(ASP:answer set programming)以及情景演算(situation calculus)等逻辑语言中都有关于遗忘的研究。其被广泛应用于最弱充分条件和最强必要条件的计算([10,26]),溯因推理([26]),相关性分析([14,24,27]),知识和信念的推理([14,35]),冲突解决([25,45]),本体分析与重用([5,19–22,31–33,37,41–43,47]),信息隐藏([31,42,47]),逻辑差异的判定([21,42]),知识库更新([13,28–30,34,46]),ASP中的非单调推理([9,11,18,38–40])等诸多领域。
关于遗忘的理论研究,主要集中在两个方面:可定义性问题和遗忘结果的计算问题。前者主要研究当前理论用某种逻辑语言表示时,遗忘结果是否依然能用该逻辑语言来表示;后者主要研究如何计算遗忘之后所得的新理论。
遗忘作为一个逻辑概念首次由Lin和Reiter于1994年([27])在命题逻辑中正式提出。其中,Lin和Reiter基于模型理论给出了命题逻辑中遗忘原子命题的定义,证明了其可定义性,且给出了遗忘结果的计算方法。Lang等人将其扩展到遗忘命题文字(literal)。([24])方良达和万海等([14]),以及林作铨教授和徐岱([44])等分别进一步将其扩展到遗忘命题公式。
模态逻辑适用于智能体的知识表示与推理。按照对知识的不同理解和要求,提出了不同的模态逻辑公理系统,其中较常用的正规模态逻辑系统有K,T,KD45,S4和S5等。([15])模态逻辑中区分客观事实与主观知识,其知识遗忘比命题逻辑中的变量遗忘要复杂的多,因为命题逻辑只要处理客观事实的遗忘问题,模态逻辑要同时处理客观事实与主观知识的遗忘问题。([16])而且在不同的模态逻辑公理系统中,遗忘还表现出不同的特性。已有研究成果表明,在K([2,36]),T([2]),KD45([13])和S5([6,46])中,知识遗忘是可定义的,但在S4中是不可定义的([7])。
为了适应多智能体场景下的知识表示与推理,多智能体模态逻辑被提出。与单智能体模态逻辑系统相对应,多智能体模态逻辑也有一些常用的正规公理系统:Kn、Tn、KD45n、S4n和S5n。由于高阶知识(关于智能体知识的知识)的引入,多智能体模态逻辑中的知识遗忘变得更加复杂。方良达和刘咏梅等将知识遗忘扩展到多智能体模态逻辑,并证明了知识遗忘在Kn,Tn,KD45n,和S5n是可定义的,在S4n中是不可定义的。([12])同时,Cate等在描述逻辑ALC中证明了统一插值的可定义性([5]),鉴于ALC与模态逻辑的对应关系([1])以及统一插值与知识遗忘的对偶关系([33]),他们实质上也给出了Kn中知识遗忘可定义的结论。
到目前为止,多智能体模态逻辑系统中的知识遗忘还无法有效计算。文献[12]中,虽然给出了常用正规模态逻辑系统中知识遗忘的可定义性结果,但其知识遗忘计算效率非常低——非初等时间复杂度。这严重影响了知识遗忘的实际应用。本文重点探讨多智能体模态逻辑系统Kn中知识遗忘的计算问题。我们采用知识编译([8])的思想,先将一般公式等价转换为一种特殊的范式公式——Kn-DNF公式,然后再计算知识遗忘。该算法的时间复杂度是Kn-DNF公式长度的多项式时间。Kn系统是最小的正规多智能体模态逻辑公理系统,其它正规多智能模态逻辑系统都从它扩展而来。虽然不同模态逻辑系统中知识遗忘的性质和计算方法都不尽相同,但Kn系统中知识遗忘的研究对其它多智能模态逻辑系统中知识遗忘的研究依然具有借鉴意义。
文章后续部分结构如下:第一部分,介绍本文研究相关的基础知识;第二部分,分析Kn中知识遗忘的重要性质;第三部分,按知识编译的思路,提出Kn中有利于知识遗忘计算的范式公式;第四部分,给出Kn中知识遗忘的计算算法,证明其正确性,分析时间复杂度,并比较相关工作;最后,总结全文并指出进一步的研究方向。
1 基础知识
本章介绍与本文研究相关的基础知识和一些符号记法。
1.1 多智能体模态逻辑
模态逻辑适用于智能体的知识表示与推理,我们参考文献[15]定义多智能体模态逻辑的语法和语义。
P表示原子命题集,A表示n个智能体的集合。通常用i,j∈{1,...,n}来指代不同的智能体。
定义1([15]).多智能体模态逻辑语言L可递归定义如下:
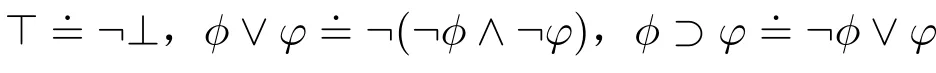
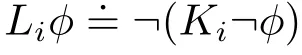
。Ki表示“智能体i知道ϕ”,Liϕ表示“智能体i认为ϕ有可能”。
多智能体模态逻辑语言L中的元素,称为公式。形如Kiϕ的公式称为正模态文字,形如Liϕ的公式称为负模态文字。不包含模态文字的公式称为客观公式。所有客观公式的集合,即为命题逻辑语言,记为Lp。var(ϕ)表示公式ϕ中出现的原子命题的集合。
通常用长度或深度来刻画模态逻辑公式的复杂程度,它们的定义分别如下。
定义2([15]).给定公式ϕ∈L,ϕ的长度为符号集P∪{¬,∧,K1,...,Kn}中的符号在ϕ中出现的次数,记为|ϕ|。
定义3([15]).在模态逻辑语言L中,公式ϕ的深度d(ϕ)为公式中模态算子的嵌套层数,其可递归定义如下:
多智能体模态逻辑的语义采用克里普克的可能世界语义([23]),通过克里普克模型与多智能体模态逻辑公式之间的满足关系给出。
定义4([15]).n个智能体的克里普克结构是一个多元组M=(W,V,R1,...,Rn),其中
•W是一个非空的可能世界集合;
•V:W →2P是一个赋值函数,指定在每个可能世界中哪些原子命题成立;
•Ri⊆W×W是W上的二元关系。
(w1,w2)∈Ri表明智能体i处于世界w1时,认为可能处于世界w2。如果用有向图来表示克里普克结构,那么(w1,w2)就表现为一条从结点w1到w2的标识为的i边,因此Ri常被称为可达关系。R=∪ni=1Ri,即所有智能体可达关系的并集,R∗表示R的自反传递闭包。令Ri(w)={w′|(w,w′)∈Ri}表示在世界w时,智能体i认为其可能所处世界的集合。类似地,R∗(w)表示从w出发,所有可达世界的集合。
定义5([15]).n个智能体的克里普克模型是一个二元组(M,w),其中M=(W,V,R1,...,Rn)是克里普克结构,w∈W是可能世界之一,被称为当前世界。
定义6([15]).克里普克模型(M,w)满足公式ϕ∈L,记为(M,w)⊨ϕ,可递归定义如下:
(M,w)⊨p 当且仅当 p∈V(w)
(M,w)⊨¬ϕ 当且仅当 (M,w)/⊨ϕ
(M,w)⊨ϕ∧φ 当且仅当 (M,w)⊨ϕ且(M,w)⊨φ
(M,w)⊨Kiϕ 当且仅当 对任意w′∈W,如果(w,w′)∈R,则(M,w′)⊨ϕ
智能体i知道ϕ(Kiϕ),当且仅当,在当前世界下,所有他认为可能的世界中ϕ都成立;智能体i认为ϕ可能(Liϕ),当且仅当,在当前世界下,存在一个他认为可能的世界中ϕ成立。我们用ϕ⊨φ表示公式ϕ的所有模型都满足公式φ,ϕ≡φ表示φ⊨ϕ且ϕ⊨φ。
正规的多智能体模态逻辑系统,都必须满足如下公理和推理规则:
A1所有命题逻辑中的公理;
A2 Kiϕ ∧ Ki(ϕ ⊃ φ)⊃ Kiφ,i=1,...,n;
R1由⊢α和⊢α⊃β,可推导出⊢β;
R2由⊢α,可推导出⊢Kiα,i=1,...,n。
仅满足上述公理和推理规则的公理系统称为Kn系统。在此基础上,根据对知识性质的不同要求,扩展出各种不同的公理系统,如Tn,KD45n,S4n和S5n等。([15])本文重点关注Kn公理系统。
1.2 Σ-互模拟
在模态逻辑的研究中,互模拟(bisimulation)是一个非常重要的概念([3]),模态逻辑中知识遗忘的定义大都基于互模拟的扩展——Σ-互模拟。我们参考文献[12]定义多智能体模态逻辑中的Σ-互模拟。
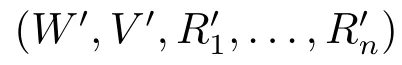
原子条件V(v)≃ΣV′(v′);
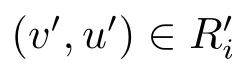
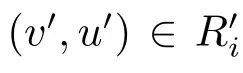
其中V(v)≃ΣV′(v′)表示可能世界v和v′中除了Σ中的命题之外,其它命题的赋值一致。
(M,w)↔Σ(M′,w′),即模型(M,w)和(M′,w′)在除了Σ中命题之外的命题上相互模拟。当Σ=∅时,Σ-互模拟实质上就是互模拟,简写成(M,w)↔(M′,w′)。显然,Σ-互模拟关系是一个等价关系,即具有自反性、传递性和对称性。Σ-互模拟具有如下重要特性。
命题1([12]).如果(M,w)↔Σ(M′,w′),给定公式ϕ∈ L,var(ϕ)∩Σ = ∅,则(M,w)⊨ ϕ当且仅当(M′,w′)⊨ ϕ。
命题1表明:两个克里普克模型Σ-互模拟,则它们满足相同的不包含Σ中原子命题的公式。
定义8([3]).给定模型 (M,w),M=(W,V,R1,...,Rn)和(M′,w),M′=(W′,V′,R′1,...,R′n),(M′,w)为(M,w)的生成子模型,当满足下列条件时:
(1)W′=R∗(w);
(2)V′(u)=V(u),如果 u ∈ W′;
(3)R′i=Ri∩(W′×W′)。
(M,w)的生成子模型中仅考虑从可能世界w出发可达的可能世界,并保留它们之间的可达关系。
命题2([3]).若(M′,w)为(M,w)的生成子模型,则两者互模拟(M,w)↔(M′,w)。
1.3 变量遗忘
Lin和Reiter基于模型理论定义了命题逻辑中的变量遗忘。([27])模态逻辑中的知识遗忘在此基础上发展起来,因此有必要介绍一下变量遗忘。
定义9([27]).给定命题逻辑的公式ϕ∈Lp和原子命题p∈P,公式ϕ′是公式ϕ遗忘p的结果,记为ϕ′≡Forget(ϕ,p),如果任意命题逻辑模型M,M ⊨ϕ′当且仅当存在模型M′⊨ϕ且M′≃{p}M。
其中,M′≃{p}M表示模型M′和M在P{p}上的真值指派一致。
命题3([27]).在命题逻辑中,若ϕ′≡ Forget(ϕ,p),则ϕ′≡ ϕ(p/⊤)∨ϕ(p/⊥)。其中,ϕ(p/⊤)和ϕ(p/⊥)分别表示将公式ϕ中的命题p分别用⊤和⊥统一替换之后的结果。
2 多智能体模态逻辑中的知识遗忘
文献[12]将文献[46]中单智能体模态逻辑系统S5中知识遗忘的定义扩展到多智能体模态逻辑。在此基础上,我们定义修正版的多智能体模态逻辑知识遗忘。
定义10.给定公式ϕ∈L和原子命题p∈P,公式ϕ′是公式ϕ遗忘p的结果,记为ϕ′≡KForget(ϕ,p),如果任意的模型(M,w),(M,w)⊨ϕ′当且仅当存在模型(M′,w′)满足 (M′,w′)⊨ ϕ 且 (M,w)↔{p}(M′,w′)。
为与命题逻辑中的变量遗忘区分,模态逻辑中的变量遗忘,特称为“知识遗忘”,记为KForget。为简单起见,我们定义的是遗忘一个原子命题p∈P。易证,遗忘一个原子命题集可以通过依次遗忘该集合中的原子命题来实现,且与遗忘的次序无关。在文献[12]的定义中要求var(ϕ′)⊆var(ϕ){p}。我们的定义放弃了这一限制条件,后面会证明这原本就是我们定义的知识遗忘的性质之一。
接下来,我们将系统分析在智能体模态逻辑系统Kn中知识遗忘的重要性质。
命题4([46]).若ϕ ∈ Lp,即ϕ是客观公式,p∈ P,则KForget(ϕ,p)≡ Forget(ϕ,p)。
该命题表明:命题逻辑中的变量遗忘实质上是模态逻辑中知识遗忘的特例。
命题5.给定 ϕ ∈ L和 p∈ P,则KForget(Kiϕ,p)≡ Ki(KForget(ϕ,p)),i=1,...,n。
证明.根据知识遗忘的定义可证,具体证明如下:
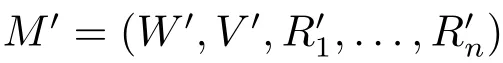
假定 (M,w)|=Ki(KForget(ϕ,p)),M=(W,V,R1,...,Rn),需证 (M,w)|=KKForget(ϕ,p),仅需证存在模型满足公式Kiϕ且与模型(M,w)在除了p之外的命题上互模拟。由(M,w)|=Ki(KForget(ϕ,p))可知,任意(w,v)∈Ri,均满足 (M,v)⊨ KForget(ϕ,p),即存在 (Mv,wv)⊨ ϕ且 (Mv,wv)↔{p}(M,v),Mv=(Wv,Vv,Rv1,...,Rvn)。对所有这样的v,将(M,v)的生成子模型分别用(Mv,wv)进行替换,并假定不同的Wv之间相互独立(彼此不相交),得到模型(M′,w)。易证 (M′,w)↔{p}(M,w)且 (M′,w)⊨ Kiϕ。
注意:若ϕ ∈ Lp,则KForget(Kiϕ,p)≡ Ki(Forget(ϕ,p))。当ϕ是一般的模态逻辑公式时,我们仅证明了在Kn中命题5成立;在其它公理系统中,KForget(Kiϕ,p)⊨Ki(KForget(ϕ,p))成立,但目前还无法证明其反向是否成立。因为其他公理系统的克里普克模型中可达关系需满足一定的性质,上述模型构成过程无法保证保持其可达关系的性质。
命题6([46]).给定ϕ1,ϕ2∈L和p∈P,则:
(1) 若 ϕ1≡ ϕ2,则 KForget(ϕ1,p)≡ K(Forget(ϕ2,p));
(2) 若 ϕ1⊨ ϕ2,则 KForget(ϕ1,p)⊨ K(Forget(ϕ2,p));
(3)KForget(ϕ1∨ ϕ2,p)≡ KForget(ϕ1,p)∨ KForget(ϕ2,p);
(4)KForget(ϕ1∧ ϕ2,p)⊨ KForget(ϕ1,p)∧ KForget(ϕ2,p)。
结论(1)表明知识遗忘的结果具有逻辑唯一性;结论(2)表明知识遗忘保持逻辑蕴涵关系;结论(3)表明知识遗忘操作对析取运算满足分配率;结论(4)表明知识遗忘操作对合取运算并不满足分配率,这给知识遗忘的计算带来困难。例如:KForget(K1(p⊃q)∧K1(q⊃r),q)≡K1(p⊃r),KForget(K1(p⊃q),q)≡⊤,KForget(K1(q⊃ r),q)≡ ⊤,显然KForget(K1(p⊃ q)∧K1(q⊃ r),q)与KForget(K1(p⊃q),p)∧KForget(K1(q⊃r),q)不等价。
定义11.给定ϕ∈L和p∈P,若存在ϕ′∈L,ϕ≡ϕ′且var(ϕ′)∩{p}=∅,则称ϕ与p不相关,记为IR(ϕ,p)。
命题 7.给定 ϕ1,ϕ2∈ L 和 p ∈ P,若 IR(ϕ1,p),则 KForget(ϕ1∧ϕ2,p)≡ ϕ1∧KForget(ϕ2,p)。
命题7表明:从一个理论(有限个公式的集合)中遗忘命题p,与p不相关的部分不受影响。
文献[46]提出了四个公设:弱化公设(W)、正保持公设(PP)、负保持公设(NP)和不相关公设(IR),刻画了S5中知识遗忘的语义特征。下面我们将证明在Kn中知识遗忘依然满足这些公设。
定理1.在多智能体模态逻辑Kn中,给定ϕ1,ϕ2∈ L和p∈ P,ϕ2≡ KForget(ϕ1,p),则满足如下条件:
(W)ϕ1⊨ϕ2,即ϕ2在逻辑上要比ϕ1弱;
(PP)任意公式φ∈L,IR(φ,p),若ϕ1⊨φ,则ϕ2⊨φ;
(NP) 任意公式 φ ∈ L,IR(φ,p),若 ϕ1/⊨ φ,则ϕ2/⊨ φ;
(IR)IR(ϕ2,p),即 ϕ2与 p不相关。
证明.根据知识遗忘定义和不相关的定义可证,具体证明如下:
(W)任意模型(M,w)⊨ϕ1,有(M,w)↔{p}(M,w)。由定义10可知,(M,w)⊨KForget(ϕ1,p),故有 ϕ1⊨ ϕ2。
(PP) 由ϕ2≡ KForget(ϕ1,p)可知,任意模型(M,w)⊨ ϕ2,必存在模型(M′,w′)⊨ϕ1且 (M,w)↔{p}(M′,w′)。由 ϕ1⊨ φ 可知,(M′,w′)⊨ φ。由 IR(φ,p)和(M,w)↔{p}(M′,w′)以及命题1可知,(M,w)⊨φ。故有ϕ2⊨φ。
(NP)若 ϕ1/⊨ φ,则存在模型 (M,w)⊨ ϕ1但 (M,w)/⊨ φ。由 (M,w)⊨ ϕ1和ϕ2≡ KForget(ϕ1,p)可知,存在 (M′,w′)⊨ ϕ2且 (M,w)↔{p}(M′,w′)。由IR(φ,p)和命题 1 可知,(M′,w′)/⊨ φ。故有 ϕ2/⊨ φ。
(IR)根据不相关的定义可知,要证IR(ϕ2,p)只需证存在公式ϕ′∈L,var(ϕ′)∩{p}=∅且ϕ′≡ KForget(ϕ1,p)。文献[12]和[5]中已证明确实存在这样的公式。
推论1.给定ϕ1,ϕ2∈L和p∈P,若ϕ2≡ KForget(ϕ1,p),则对任意φ∈L且IR(φ,p),ϕ1⊨ φ当且仅当ϕ2⊨ φ。
推论1表明从一个理论遗忘一个命题,所得新理论与原理论在与被遗忘命题无关的结论中,保持逻辑一致。
推论2.给定公式ϕ∈L和p∈P,φ≡KForget(ϕ,p),则存在公式ϕ′∈L,ϕ′≡φ且 var(ϕ′)⊆ var(ϕ){p}。
证明. 对任意 p′∈ Pvar(ϕ),有 IR(ϕ,p′)。由命题 7 可知 ϕ ≡ KForget(ϕ,p′)。令ϕ′≡ KForget(KForget(ϕ,p′),p),即由 ϕ 依次遗忘 {p}∩Pvar(ϕ)中的原子命题得到 ϕ′。显然,ϕ′≡ φ 且 var(ϕ′)⊆ var(ϕ){p}。
推论2,充分说明在定义知识遗忘时,不必如[12]中那样显式约束var(ϕ′)⊆var(ϕ){p}。
命题8([12]).在Kn中,对任意公式ϕ∈L和原子命题p∈P,均存在公式ϕ′∈L使得 ϕ′≡ KForget(ϕ,p)。
命题8表明:在多智能体模态逻辑Kn中,知识遗忘是可定义的。
3 Kn析取范式
由命题3可知,命题逻辑中的变量遗忘可以通过简单的语法替换来计算。但是,该方法无法推广到模态逻辑。看一个简单的例子:给定ϕ=K1p∧¬K1q∧¬K1¬q,显然ϕ(q/⊤)≡ ⊥和ϕ(p/⊥)≡ ⊥,故而ϕ(p/⊥)∨ϕ(p/⊥)≡ ⊥,显然KForget(ϕ,q)不应该是⊥。由命题6可知,由于知识遗忘操作对合取运算并不满足分配率,因此尽管有命题4和命题5的性质,依然无法直接将模态逻辑中知识遗忘的计算转换为命题逻辑中的变量遗忘来计算。文献[46]在单智能体模态逻辑S5中,提出了一种析取范式(S5-DNF),通过将一般公式转换成与之等价的析取范式,该范式公式的知识遗忘可以转换成命题逻辑的变量遗忘来计算。但是,S5-DNF充分利用了S5模态逻辑系统中可达关系是等价关系的特性,无法扩展到Kn系统。本章从有效计算知识遗忘的角度,提出Kn系统中的析取范式(Kn-DNF)。
定义12.Kn–析取范式,递归定义如下:
其中,B⊆A,φ∈Lp,δi和ηij均为Kn-DNF,且满足对任意ηij均有ηij⊨δi。
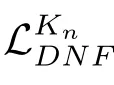
命题9.对于任意的α,β,γ∈L,在Kn中下列等价式成立:
式(1)和(2)是德•摩根定律,式(3)是双重否定律,式(4)和(5)是模态算子Ki和Li之间的对偶关系,式(6)是合取对析取的分配律,式(7)是正模态文字的合并,式(8)是正负模态文字的结合。当然,在Kn中也满足其它的等价式,例如:吸收率,结合律和交换律等,这里只列出我们所需的主要等价式。借助这些等价式,可将一般多智能体模态逻辑公式转换成与之等价的Kn-DNF公式,具体算法参见算法1。
算法1.transfer(ϕ)//将公式ϕ∈L转换为等价的Kn-DNF公式
输入:ϕ∈L
2.利用等价式(1)–(5)将ϕ等价转换为仅由正(负)模态文字和命题公式通过联结词∧或∨组成的公式ϕ′;
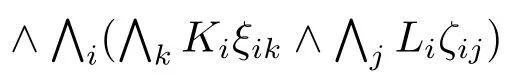
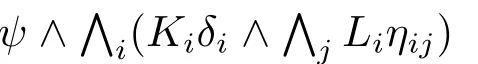
5.return ϕ′′′(δi/transfer(δi),ηij/transfer(ηij));//递归调用该算法将 ϕ′′′中的子公式δi和ηij分别转换为等价的Kn-DNF公式,进行等价替换后返回
注意:在算法1中,经过步骤2之后,否定(¬)仅允许出现在命题公式的前面,但并不严格要求只出现在原子命题的前面;步骤3中利用的(合取对析取的)分配律和步骤4中利用的(正负模态文字的)结合律均会导致公式长度的增长,但导致公式长度增长的主要原因在步骤3,它会导致公式长度指数倍的增长,就像在命题逻辑中DNF公式的转换过程一样。步骤4仅导致公式长度多项式倍的增长。步骤1和2均可在公式长度的多项式时间内完成。因此整个转换算法的时间复杂度是公式长度的指数时间。
定理2.给定任意ϕ∈L,均可等价转换为Kn-DNF公式,且公式长度在最坏情况下是原公式长度的指数倍。
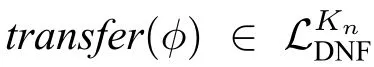
例1.ϕ = ¬(p∧¬q)∧¬(K1p∧K2q)∧K1(K2p∨K2¬p)∧K2p∧K1r∧L2r,p,q,r∈ P。将ϕ转换为Kn-DNF公式。
根据定理2,虽然一般多智能体模态逻辑公式都可转换为与之等价的Kn-DNF公式,但是会导致公式长度的增长,在最坏情况下,Kn-DNF公式相对于原公式在长度上可能会有单指数倍的膨胀。但我们会证明,Kn-DNF公式非常适用于知识遗忘的计算。
4 Kn中知识遗忘的计算
我们采用了知识编译([2])的思想来计算Kn中的知识遗忘。主要思路是:首先将一般模态逻辑公式等价转换成Kn-DNF公式,然后利用Kn-DNF公式计算知识遗忘的便利性,有效地计算知识遗忘。
4.1 知识遗忘计算定理
知识编译是解决知识推理难问题的方法之一,其主要思想是:将源知识库转换成特定形式的知识库(目标知识库);在目标知识库中,一些推理问题会变得简单易实现。其关键在针对特定的推理问题,选择适合的目标知识库表示形式。我们提出的Kn-DNF公式就是易于计算知识遗忘的目标知识库形式。
定理3.给定任意Kn-DNF公式ξ,其知识遗忘KForget(ξ,p)可递归计算如下:
其中φ∈Lp,Forget(φ,p)表示命题逻辑中的变量遗忘;δi和ηij均为Kn-DNF公式,且对任意ηij均有ηij⊨δi。
证明.定理中的(1)–(3)项显然成立,这里仅对(4)加以证明,具体证明如下:
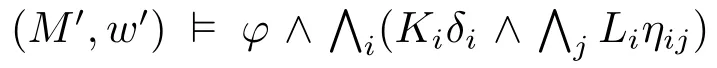
由定理3知,一个Kn-DNF公式知识遗忘的结果依然是一个Kn-DNF公式。这有利于后续知识遗忘的计算。
4.2 算法与复杂度分析
由定理3可知,Kn-DNF公式的知识遗忘可以高效计算。由定理2可知,任意多智能体模态逻辑公式均可等价转换为Kn-DNF公式,又由命题6可知,若两个公式等价,则其知识遗忘也等价。因此,不难给出Kn系统中一般公式的知识遗忘计算算法,具体参见算法2。
算法2.Kn系统中知识遗忘的计算
输入:ϕ∈L和p∈P
输出:KForget(ϕ,p)
1.将ϕ等价转换成Kn-DNF公式ϕ′=transfer(ϕ);
2.计算 KForget(ϕ′,p);
3.return KForget(ϕ′,p);
算法2即可实现Kn系统中一般公式知识遗忘的计算方法,其正确性由定理2,定理3以及命题6可证。步骤1(即知识编译)时间复杂度为|ϕ|的指数时间,步骤 2 时间复杂度为 |ϕ′|的多项式时间,由于 |ϕ′|=2O(|ϕ|·log|ϕ|),因此整个算法的时间复杂度为2O(|ϕ|·log|ϕ|),即原公式长度的指数时间。知识编译仅需做一次,就可供多次知识遗忘计算使用。在多次计算知识遗忘时,知识编译的时间开销会得到一定的补偿。
例2.在Kn系统中,给定公式ϕ=(p⊃q)∧K1(q∧K2r∨¬q∧K2¬r)∧L1(q⊃r),计算 KForget(ϕ,q)。
首先,ϕ≡(p⊃q)∧K1(q∧K2r∨¬q∧K2¬r)∧L1(q∧r∧K2r∨¬q∧K2¬r);
接着,KForget(ϕ,q)≡ K1(K2r∨K2¬r)∧L1(r∧K2r∨K2¬r)。
4.3 相关工作
文献[12]中,证明了包括Kn在内的一些常用正规模态逻辑系统中知识遗忘的可定义性,但其知识遗忘计算效率非常低——为非初等时间复杂度。
Janin和Walukiewicz提出了另一种多智能体模态逻辑析取范式公式,被称为覆盖析取范式公式(CDNF:cover disjunctive normal formula,[17]),研究结果表明该析取范式也适合知识遗忘的计算。([5,17])
定义13([17]).给定智能体集合A和公式Φ⊆L集合,覆盖模态算子∇,i∈A可定义为:
(M,w)⊨∇iΦ,当且仅当w在M 中的直接Ri后继v满足且仅满足Φ中的公式,即Φ中覆盖了w的直接Ri后继可满足的公式。故模态算子∇i也被称为“覆盖模态算子”。显然∇i{⊤}≡⊤,∇i{⊥}≡⊥,∇i∅≡Ki⊥。
定义14([17]).覆盖析取公式,可递归定义如下:
其中,π是一致的命题文字合取,Φ1,...,Φn均为覆盖析取公式的有限集合。
所有CDNF公式的集合记为LCDNF。已有研究结果表明:任意模态逻辑公式,均可等价转换成CDNF公式,在最坏情况下,可能会导致公式长度单指数倍的膨胀。([5])
命题10([5]).给定任意CDNF公式ξ,其知识遗忘KForget(ξ,p)可递归计算如下:
(1)KForget(⊤,p)≡ ⊤;
(2)KForget(⊥,p)≡ ⊥;
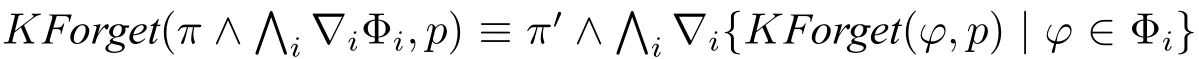
从π中删除与p相关文字(p或¬p)之后的命题文字合取。
定义15.给定逻辑语言L和L′,如果对于任意的ϕ′∈L′,均存在ϕ∈L,满足ϕ≡ϕ′且|ϕ|≤f(|ϕ′|),其中f:N→N是多项式函数,则称L至少和L′一样简洁(succinct),记为 L ≤ L′。
如果L≤L′且L′/≤L,则称L比L′简洁,记为L 例3.借助CDNF公式计算例2中的KForget(ϕ,q)。 从例2和例3可知,将一般公式转换成Kn-DNF或CDNF之后,均可计算其知识遗忘,且两者所得结果逻辑等价(CDNF公式与一般公式之间的转换参考文献 [5])。不难看出,即使采用 ∇iΦ 作为 ∧φ∈ΦLiφ∧Ki(Vφ∈Φφ)的缩写,Kn-DNF公式比CDNF公式仍要简洁得多。而且采用Kn-DNF公式可以避免部分子公式知识遗忘的重复计算。 本文在多智能体模态逻辑系统Kn中,对知识遗忘进一步展开研究。系统分析了知识遗忘的重要性质;基于知识编译,提出一种Kn系统中知识遗忘计算的有效算法,与已有算法相比,我们的算法更高效。Kn是最小的正规多智能体模态逻辑系统,其它正规多智能模态逻辑系统都在其基础上扩展而来。尽管不同模态逻辑系统中知识遗忘的性质和计算方法都不尽相同,但本文的研究对其它多智能模态逻辑系统中知识遗忘的研究依然具有借鉴意义。 下一步研究,一方面将考虑引入包括公共知识(common Knowledge)和分布知识(distributed Knowledge)在内的群体知识之后,知识遗忘的计算问题。另一方面,将继续探讨在其他多智能体模态逻辑系统(如:KD45n,S5n)中的知识遗忘计算问题。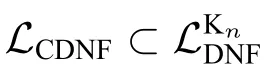

5 结论与展望
