一种宽温度范围低温度系数的CMOS带隙基准电路

任贺宇，王 军，赵传阵

（1.天津工业大学电子与信息工程学院，天津 300387；2.天津工业大学天津市光电探测技术与系统重点实验室，天津 300387）

带隙基准（BGR）电路广泛应用于各种模拟和混合信号电子器件中，如AD/DA、PWM控制器、运算放大器、LDO和PLL等[1-2].BGR的精度会显著影响系统的性能[3-4]，如，温度传感器的精度不仅依赖于温度敏感元件，还直接取决于基准电压的精度.为得到低温度系数（TC）的BGR，相关研究提出了多种曲率补偿技术[1，3-15].文献[1]利用零温度系数节点的二级原理来提高基准电压的精度，并采用MOSFET的漏源电压反馈降低零温度系数节点对温度的敏感度，同时采用有源衰减器和阻抗适应补偿以提高基准电压的电源抑制比.文献[3]采用基于MOSFET的MOS BGR和基于BJT的一阶曲率补偿BGR电路，实现2个具有相反温度特性的基准电压，并采用电流镜将这2个基准电压叠加，实现高阶非线性曲率补偿以提高基准电压的精度.文献[4]采用可调节曲率补偿技术（即分段补偿技术），在3段温度区间对基准电压进行不同曲率的补偿以提高其精度.文献[5]采用2个传统一阶BGR电路，实现2个具有相反温度特性的基准电压，并基于这2个基准电压设计加法电路，实现高阶非线性曲率补偿.文献[15]采用电平移位技术抑制电阻对基准电压的影响.本文根据分段补偿思想[4-9]，提出基于高阶非线性补偿的5段分段补偿技术，在-40~125℃的宽温度范围内，设计了一种高精度BGR电路，仿真结果表明该电路的TC为0.05×10-6/℃.

1 BGR设计方法

一阶BGR通常采用双极晶体管（BJT）基极-发射极电压（VEB）和2个BJT基极-发射极电压的差电压（ΔVEB）相互补偿的方式，获得TC较低的基准电压.ΔVEB与温度呈正相关关系，VEB与温度呈负相关关系，其表达式为[14]

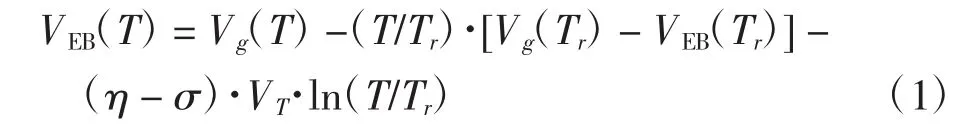
其中：Vg（T）是带隙电压；η是工艺常数；Tr是参考温度；T是温度；VT是热电压；σ是与流过BJT的电流IBJT相关的参数，当IBJT是PTAT电流时，σ=1，当IBJT与温度无关时，σ=0.根据式（1），VEB的温度特性主要由一阶线性和高阶非线性构成，然而ΔVEB的温度特性仅包含一阶线性，因此对VEB的高阶非线性补偿可以提高BGR的精度.高阶非线性补偿的实现如图1所示[9].

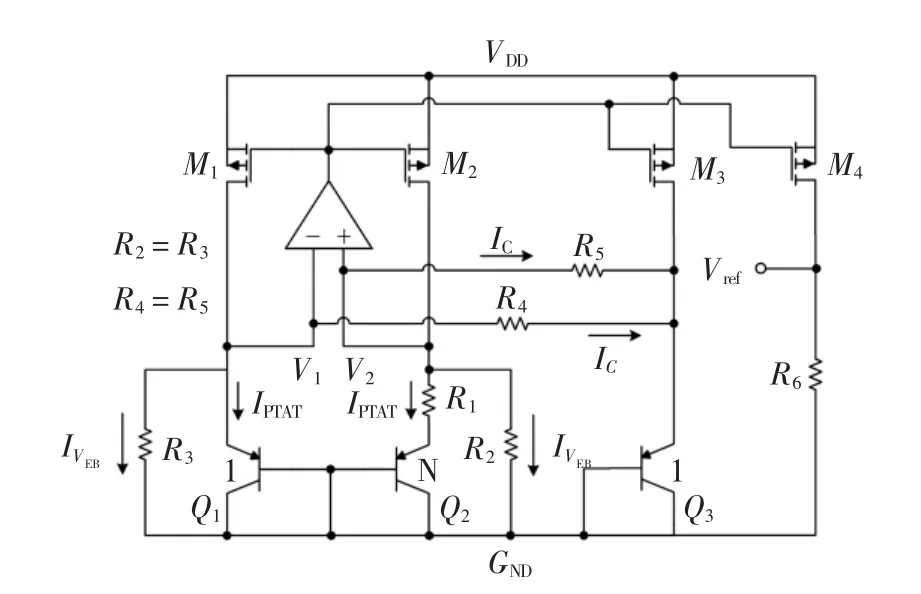
图1高阶非线性补偿电路Fig.1 High-order nonlinear com pensation circuit

图1 中，运算放大器使得V1=V2，因此IQ1，Q2是PTAT电流，IQ3近似与温度无关.由式（1）可得[15]

其中ΔVEB，Q2-Q3（T）呈现高阶非线性温度特性，因此Vref可表示为

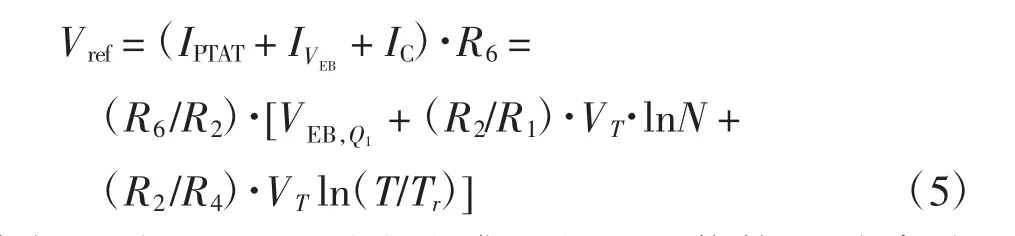
其中：N为Q2和Q1之间的集电极电流倍数；IC为高阶非线性补偿电流.适当选取R1、R2和n，可以消除VEB，Q1的一阶线性温度特性，当R4，5=R2（/η-1）时，可以消除VEB，Q1的高阶非线性温度特性.采用高阶非线性补偿后的基准电压如图2所示.

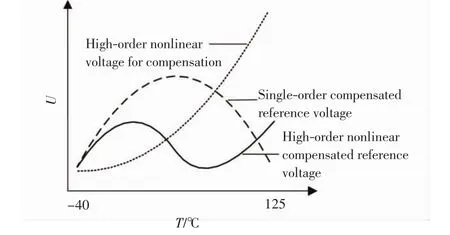
图2 高阶非线性补偿原理Fig.2 Princip le of high-order nonlinear com pensation

2 5段分段补偿技术及电路实现

经高阶非线性补偿后，BGR的精度一般为1~10×10-6/℃[15]，尽管还有多种提高BGR精度的补偿技术[16-18]，但其基准电压仍有较大的TC.为进一步提高BGR的精度，本文提出基于高阶非线性补偿的5段分段补偿技术，将高阶非线性补偿和分段补偿相结合，以实现高精度的BGR电路.

2.1 分段补偿技术

分段补偿技术是在不同温度区域内，采用不同曲率的电压（分段补偿电压）对基准电压进行补偿，从而改善其精度.本文采用的分段补偿技术的基本实现电路见图3.

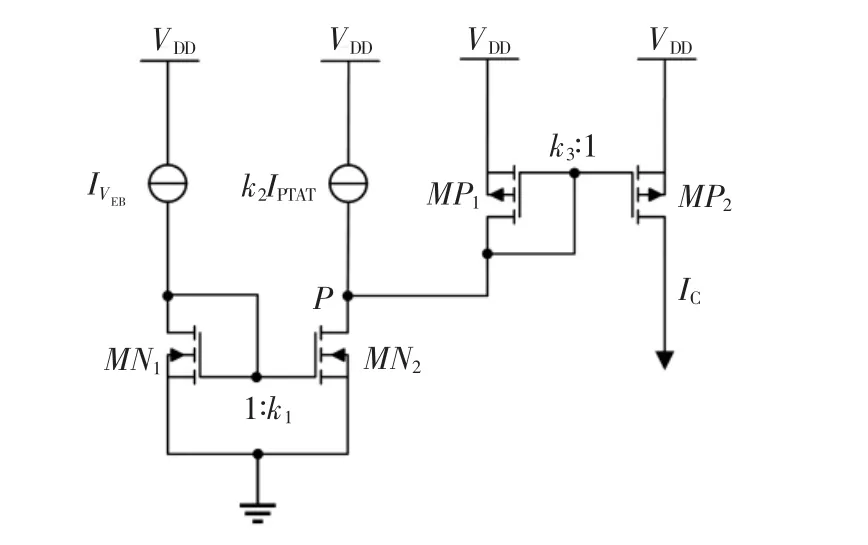
图3 分段补偿实现电路Fig.3 Im plementation circuit of typical piecewise com pensation

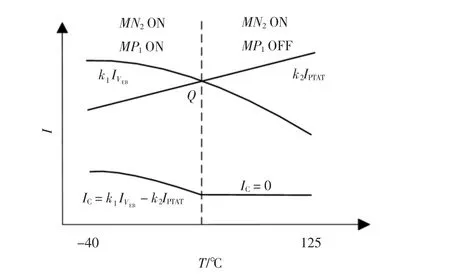
图4分段补偿原理Fig.4 Principle of piecewise compensation

图4 中，根据基尔霍夫电流定律（KCL），在低温区域，k1IVEB＞k2IPTAT，因此IC=k1IVEB-k2IPTAT，在高温区域，k1IVEB＜k2IPTAT，MP1因不能提供流向电源VDD的电流而截止，因此IC=0.分段补偿电流的分段点为正负温度系数电流的交点Q.通过调整k1和k2的大小可以改变Q点对应温度的大小.

将高阶非线性补偿后的基准电压分为5段，采用图4所示的分段补偿技术，实现5段分段补偿以提高BGR精度，其技术原理如图5所示.

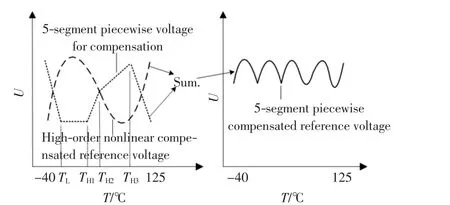
图5 5段分段补偿技术原理Fig.5 Principle of 5-segment segmentation compensation technology

2.2 电路实现

本文提出的BGR整体电路见图6.采用10组电流镜组合实现电流加减电路，在-40～125℃的温度范围内，对正负温度系数电流进行比例复制和加减运算，得到具有5段分段温度特性的补偿电流和电压，以实现基于高阶非线性补偿的5段分段补偿.

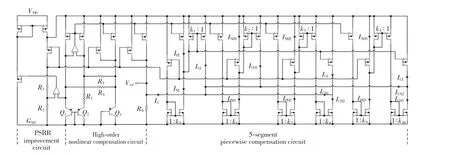
图6 BGR电路Fig.6 BGR circuitr

图6 中，IPH1、IPH2、IPH3和IPL为IPTAT的比例复制电流，INH1、INH2、INH3和INL为ICTAT的比例复制电流，ICH1、ICH2、ICH3和ICL叠加组成最终的分段电流IC.图5的5段分段补偿电压中的4个电压折点的温度从左至右分别记为TL、TH1、TH2、TH3.k1，k2，…，k10是每个电流镜的比例，其中：k1，…，k5决定补偿电流的大小，k6，…，k10决定TL、TH1、TH2、TH3的值.

（1）当T＜TL时，INH1＞IPH1，INH2＞IPH2，INH3＞IPH3，INL＞IPL，根据KCL，ICH1=ICH2=ICH3=0，IC的计算公式为

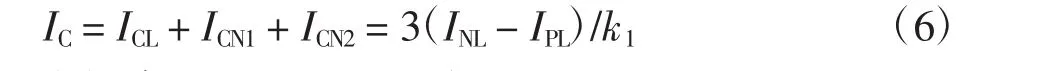
（2）当TL＜T＜TH1时，INH1＞IPH1，INH2＞IPH2，INH3＞IPH3，INL＜IPL，5段分段补偿电路中所有电流均为0，因此IC=0.

（3）当TH1＜T＜TH2时，INL＜IPL，INH2＞IPH2，INH3＞IPH3，INH1＜IPH1，因此ICL=ICH2=ICH3=ICN1=ICN2=0，IC的计算公式为

（4）当TH2＜T＜TH3时，INL＜IPL，INH3＞IPH3，INH1＜IPH1，INH2＜IPH2，因此ICL=ICH3=ICN2=0，IC的计算公式为

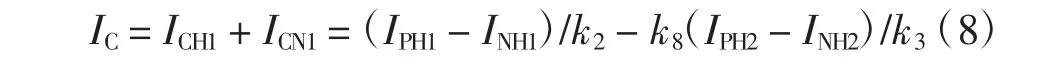
（5）当T＞TH3时，INL＜IPL，INH1＜IPH1，INH2＜IPH2，INH3＜IPH3，INH1＜IPH1，因此ICL=0，IC的计算公式为

3 仿真验证

本文得到的5段分段补偿电压、高阶非线性补偿后的基准电压及最终的5段分段补偿后的基准电压如图7所示.

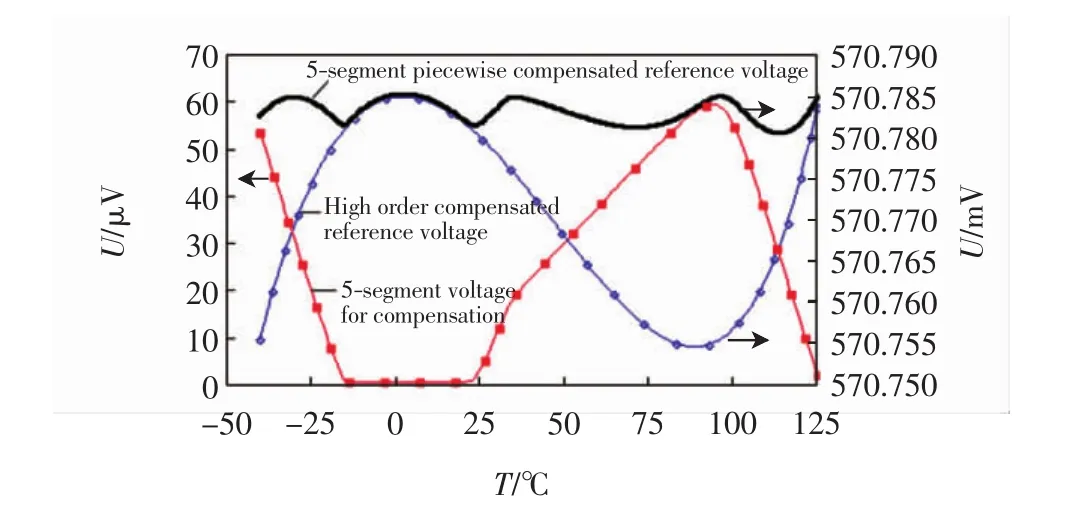
图7 5段分段补偿仿真结果Fig.7 Simulation results of 5-segment piecewise com pensation

由图7可见，在-40～125℃的温度范围内，高阶非线性补偿后基准电压的总温漂约为30 μV，即TC约为0.32×10-6/℃；5段分段补偿后基准电压的总温漂约为4.5 μV，即TC约为0.05×10-6/℃，比高阶非线性补偿提高了约6.7倍.

本文考虑了基准电压在电源方面的可靠性，进行了PSRR（电源抑制比）和线性调整率仿真，仿真结果如图8和图9所示，电压仿真范围为2.5～5 V.

由图8和图9可见，PSRR约为-100 dB@dc，在2.5～5 V的电源范围内线性调整率约为11.8 μV/V，这表明BGR对电源具有良好的抗干扰能力.

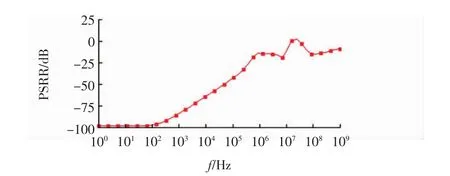
图8 PSRR仿真结果Fig.8 Simulation result of PSRR

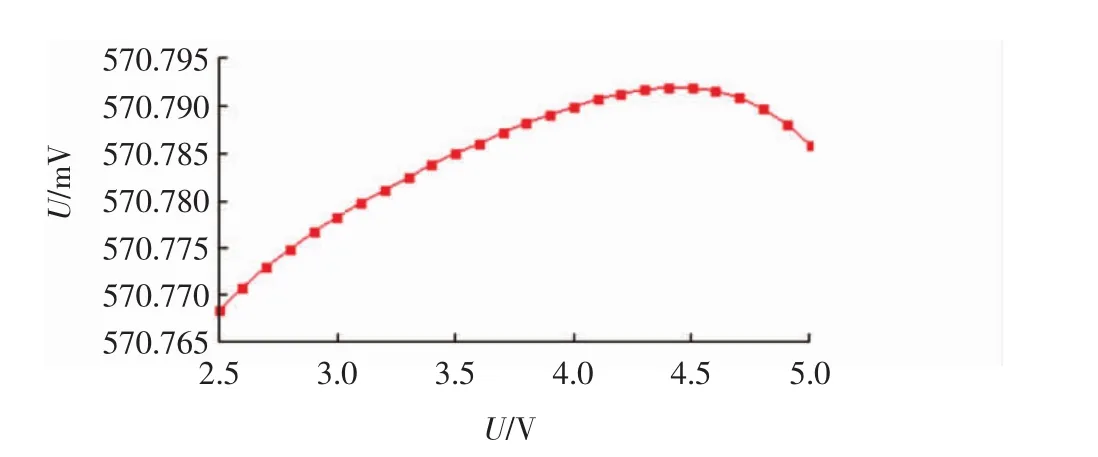
图9 线性调整率仿真结果Fig.9 Simulation result of linearity

将本文设计的BGR的技术性能和指标与一些现有的BGR进行比较，比较结果见表1.其中：Vol.Supply为BGR的供电电压，Current为BGR的工作电流，Ref.Voltage为BGR的基准电压，Tem.Range为BGR的工作温度范围，Line Reg.为BGR的线性调整度，Area为BGR的芯片或版图面积，CMOS process为BGR采用的工艺.由表1可见，本文设计的BGR的性能优于现有技术，此外，本文中基准电压的线性调整率和功耗等性能也比较良好.

表1 本文工作与现有技术的比较Tab.1 Comparison between this paper and priorart designs

4 结论

采用基于高阶非线性补偿的5段分段补偿技术，实现了高精度、低功耗的BGR电路.在-40～125℃的宽温度范围内，高阶非线性补偿后基准电压的精度约为0.32×10-6/℃；采用5段分段补偿技术后，基准电压的精度优化至0.05×10-6/℃，相比高阶非线性补偿，基准电压的精度优化了约6.7倍.BGR整体电路的工作电流约为28 μA，电源抑制比（PSRR）约为-100 dB@dc，线性调整率约为11.8 μV/V.