两种Sobolev空间之间的嵌入范数

胡增周，王 薇，许贵桥

（1.河北省城乡建设学校，石家庄 050031；2.天津师范大学 数学科学学院，天津 300387）

1 引言与预备知识

求函数空间上数值问题的满足一定精度的解所必须搜集的最小信息量，是信息复杂度理论研究的核心问题，其中易处理性问题是目前的研究热点[1-5].当前研究最多的是基于单变量第二类Sobolev空间与第一类Sobolev空间的多元问题的易处理性，而不同函数空间之间的嵌入范数是研究多元问题易处理性的主要工具[6-10].设

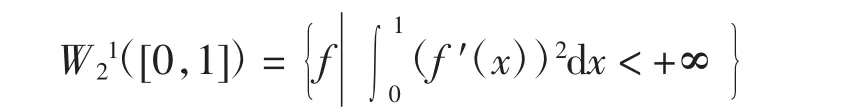
且f是局部绝对连续的.在W21（[0，1]）上引入第一类Sobolev空间H1，其相应的范数为

同时，在W21（[0，1]）上引入第二类Sobolev空间H2，其相应的范数为

H2称为以c∈[0，1]为锚的Sobolev空间，其中c称为锚.显然，H1与H2之间是互相嵌入的，文献[8]对于锚取端点（即c=0）的H1与H2的嵌入范数做了研究，得到了嵌入范数的准确值，而在许多研究如文献[9，11-13]中，c的值都是任意的，本文对任意c∈[0，1]，得到了嵌入范数的准确值.

2 主要结论

首先引入2种空间之间嵌入的定义.记

下面引入算子范数的定义.设F、G为2个线性赋范空间，若算子I：F→G为一个线性有界算子，则线性算子I的范数为

定理设I1、I2定义如式（1）和式（2），则

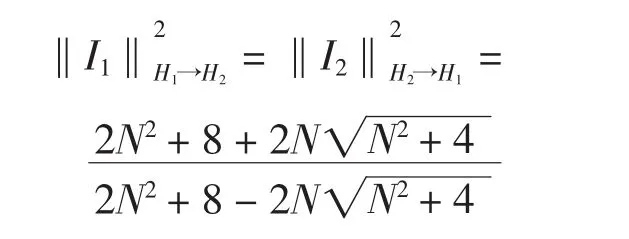
其中∈[0，1].

证明先计算‖I1‖H1→H2.记F=W21（[0,1]）.由定义知

对f（x）做余弦展开得

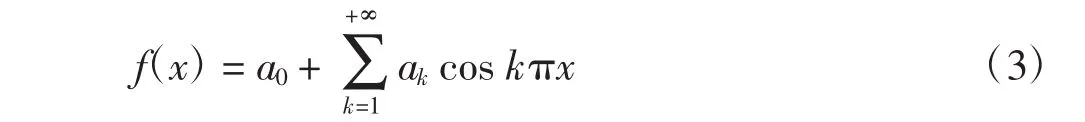
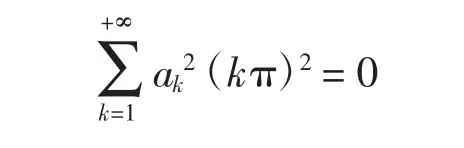
由此可得

由式（3）和式（4）得

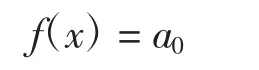
因此有

由式（3）和式（6）以及Cauchy-Schwarz不等式可得

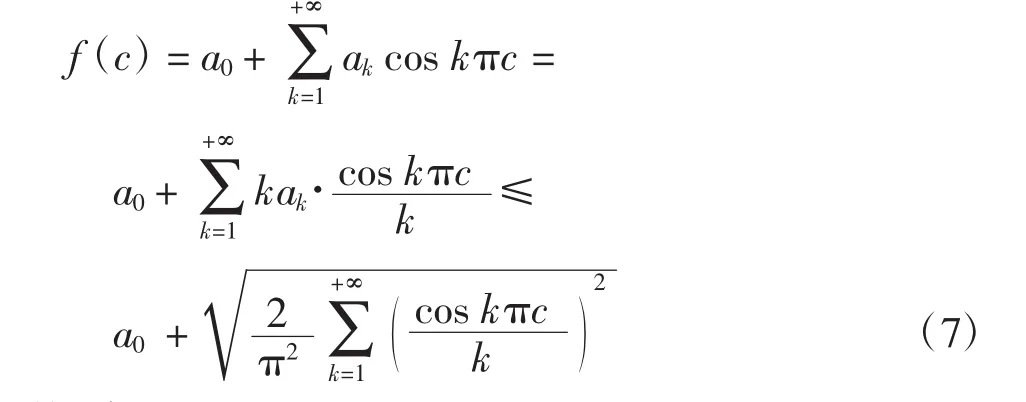
另外，令

则ak满足且有

将f（x）=（x-1）2在（0，1）上展开成余弦级数，有

令x=2c，则有

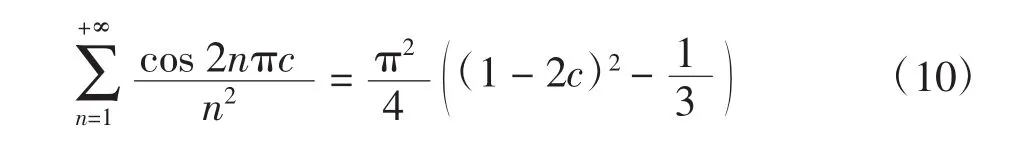
将式（10）代入式（9）得

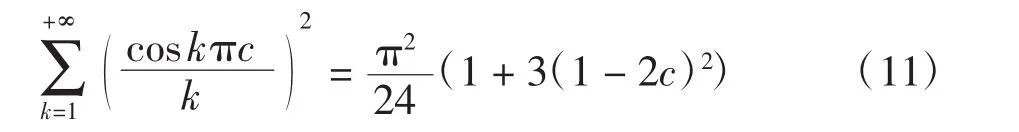
由式（7）、式（8）和式（11）可得

对固定的a0，记其为a，则有

因此

令

对g（a）关于a求导，可得g（a）当a=时取得最大值，且其最大值为

下面计算

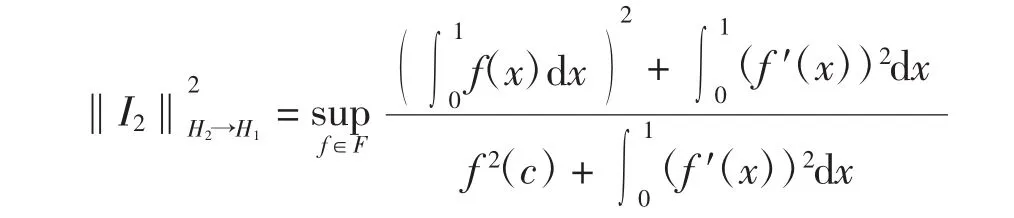
其中c∈[0，1].如果则f′（x）几乎处处为0，即f（x）=a，a为常数，则显然有

对式（14）两边同时积分得

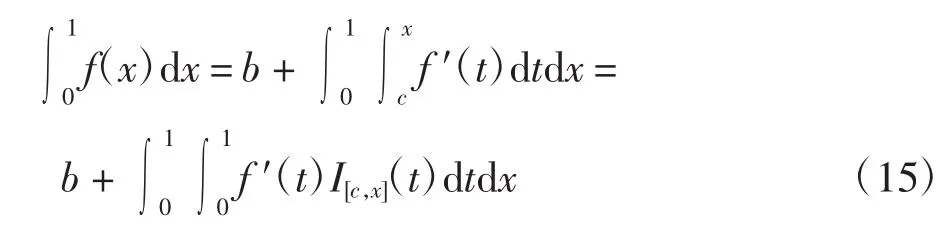
由Fubini积分交换定理得

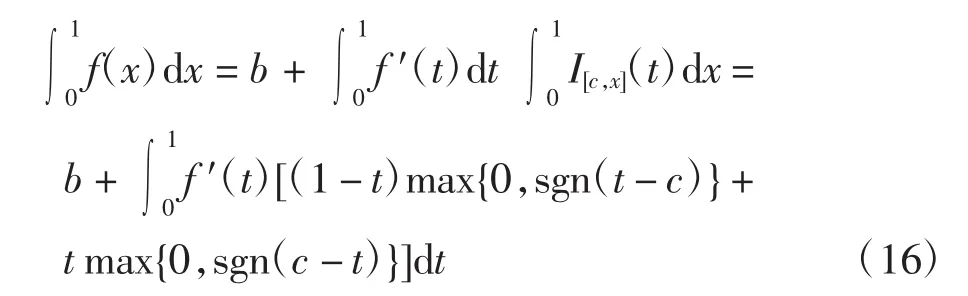
由Cauchy-Schwarz不等式可得

由式（16）和式（17）可得

此外，令

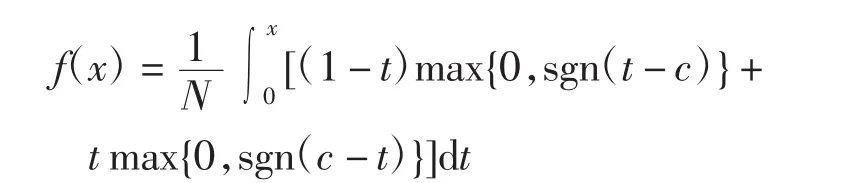
则f（x）同时满足由此结合式（18）可得

由式（19）得

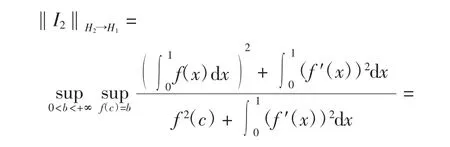
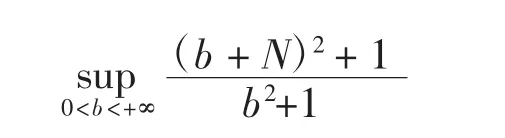
注：当c=0时，由式（13）得

文献[8]给出了上面的等式成立，但没有给出具体的证明，本文证明了文献[8]的结论，并对任意c∈[0，1]给出了该嵌入范数的具体值.