差速泵叶轮边缘结构对转矩特性的影响

徐高欢 赵华成 刘 武 谢荣盛

(浙江水利水电学院机械与汽车工程学院， 杭州 310018)

0 引言

差速泵是一种新型容积泵，其工作原理是依靠叶轮在旋转过程中相邻叶片差速转动实现容积变化。相比其他容积泵，其排量体积比大，容积效率较高，在大型植保机械、滴灌等领域具有广泛应用前景[1-5]。混合高阶傅里叶非圆齿轮驱动的差速泵，其流量脉动率、容积效率及驱动非圆齿轮不根切最大模数等性能在四叶片差速泵中最优[6]，但在试验中发现，差速泵样机在负载状态下具有明显的周期性冲击现象，而在空载状态不存在。

陈明等[7]在研究中发现，差速泵在运行过程中轴和轴承会出现很大冲击，差速泵的容积腔存在闭死容积，少量液体介质导致困液。为此文献[8-9]提出利用泄压阀引出困液，但是差速泵在困液极小的情况下，仍产生明显冲击。泵的冲击原因十分复杂，一般可以分为流体冲击和机械传动冲击[10-13]，流体冲击主要有水击、压力脉动等，机械传动冲击主要是因设计不合理或加工、安装误差引起的，如传动不平衡等[14-19]。差速泵除驱动系统存在正常交变载荷外，在排液、吸液过程中还存在水锤效应，这是造成周期性冲击的主因之一[20]。

为提升差速泵运行平稳性，本文进行数值计算和试验研究。首先，建立差速泵数值计算模型，利用数值计算方法研究差速泵腔内压力分布、流场和驱动非圆齿轮副的流固耦合作用，分析和比较不同叶片边缘在吸排液工况交替下对转矩特性的影响，最后试验验证差速泵叶片边缘圆角优化对改善流场及减缓周期性冲击的有效性。

1 非圆齿轮驱动差速泵基本原理及计算模型构建

1.1 结构

根据差速泵工作原理，容积腔随驱动机构的不等速传动实现容积空间周期性变化和周向转移[21]。四叶片差速泵结构如图1所示。

图1 四叶片差速泵结构图Fig.1 Structure diagrams of four-blade differential pump 1.内轴 2.前轴套 3.前壳体 4.泵壳 5.叶片销 6.叶轮 7.后壳体 8.后轴套 9.端盖 10、17.有骨密封圈 11.滚动轴承 12、16.O型密封圈 13、14.端面密封圈 15.滚针轴承 18.叶片1 19.叶片2 20.叶片3 21.叶片4 22.排液口(1) 23.吸液口(1) 24.排液口(2) 25.吸液口(2)

1.2 计算模型构建及叶片边缘优化

混合高阶傅里叶非圆齿轮驱动的四叶片差速泵中每一对非圆齿轮副分别驱动轴和轴套，由轴驱动的2个叶片组成叶轮1，由轴套驱动的2个叶片组成叶轮2，在两对非圆齿轮副不等速传动作用下，叶轮1和叶轮2在周转过程中实现差速运动，4个容积腔分别实现吸液和排液。差速泵传动系统三维图如图2所示，差速泵叶轮和腔体分布如图3所示。

图2 差速泵传动系统三维图Fig.2 3D diagram of differential pump drive system 1.主动齿轮2 2.主动齿轮1 3.从动齿轮1 4.从动齿轮2 5.前轴套 6.内轴 7.叶轮1 8.叶轮2 9.后轴套

图3 叶轮和腔体分布Fig.3 Distribution of impellers and cavities 1.排液口2 2.第3腔 3.第2腔 4.进液口1 5.叶轮2 6.排液口1 7.第1腔 8.叶轮1 9.第4腔 10.进液口2

数值计算模型的傅里叶非圆齿轮节曲线参数a0=35、a1=1、a2=0.2、b1=0.02、b2=0.15，非圆齿轮节曲线变性系数为1，非圆齿轮阶数比1∶2，叶轮外半径为90 mm，叶轮轴半径为20 mm，叶片厚度为50 mm，进出口和叶片角角度差2°，由于试验传感器采样频率为500 Hz，为了避免高速带来额外机械冲击及振动的干扰，仿真和试验转速均设为90 r/min。由于主动齿轮和从动齿轮阶数比1∶2，所以叶轮平均转速为45 r/min，旋转一周为1.33 s，设置该值为数值计算总时间。为研究叶轮边缘对差速泵流场压力分布和传动系统转矩特性的影响，设计2种差速泵叶轮：普通叶轮和顶部边缘圆角优化叶轮。叶轮优化后的顶部边缘圆角半径为2.8 mm，如图4所示。

图4 差速泵叶轮的叶片Fig.4 Blades of differential pump impellers

2 不同叶片边缘的流体域及耦合转矩数值计算

差速泵计算模型比较规则且为对称分布，利用UG建立计算域三维模型，再导入Workbench中进行网格划分，网格主要采用四面体非结构性网格对模型进行划分[22-24]，最大网格尺寸设为0.2 mm，最小设为0.05 mm，网格单元总数约为38.52万个，进出口设置成标准大气压。为比较不同叶轮边缘对差速泵的影响，在Workbench平台中构建流体域和驱动系统的流固耦合分析模型，通过对差速泵不同叶轮的吸、排液工况的仿真计算，得出叶轮边缘优化前后对转矩和驱动系统冲击的影响。以下分析以第1、3腔吸、排液切换过程中流体域数值计算为例，并同时计算叶轮1和叶轮2的耦合转矩。

图5 第1、3腔吸液、排液切换过程4个腔压力分布Fig.5 Pressure distributions when No.1 and No.3 displacement chamber were switched from suction to discharge

2.1 第1、3腔吸液、排液切换过程中流体域数值计算及结果分析

当第1、3腔吸液，第2、4腔排液即将结束时，叶轮1和叶轮2的转动速度接近等速，叶轮优化前如图5a、5c、5e所示，第1、3腔与进口隔开迅速，容积腔未充满而关闭进口，腔内形成大面积负压区域，容易形成空化，造成流体振动。第2、4腔与出口瞬间隔开，出口1、2压力瞬间下降，形成水锤效应。叶轮优化后如图5b、5d、5f所示，第1、3腔与进口隔开存在过渡区，第1、3腔与进口的压力存在明显的渐变过程，形成的负压区域较小，充容饱满，不容易形成空化，减少流体振动。第2、4腔与出口隔开同样存在过渡区，从压力分布看，第2、4腔与出口存在渐变过程，如图5f压力分布所示，第2、4腔排液结束后为均匀负压，容积腔排液较为彻底。

2.2 第1、3腔排液、吸液切换过程中流体域数值计算及结果分析

当第2、4腔吸液，第1、3腔排液即将结束时，叶轮1和叶轮2的转动速度同样接近等速，叶轮优化前如图6a、6c、6e所示，第1、3腔与出口隔开迅速，容积腔内液体并未排完，第1、3腔形成较大内压，形成困液区，造成困液冲击。第2、4腔与进口瞬间隔开，第2、4腔未充满前压力瞬间下降，形成较大负压区，容易产生空化，造成流体振动。叶轮优化后如图6b、6d、6f所示，第1、3腔与出口隔开存在过渡区，第1、3腔与出口的压力存在明显的渐变过程，如图6d、6f所示，由于叶轮圆弧过渡区的存在，液体排出较为彻底，排液腔形成明显负压，减少困液。

图6 第1、3腔排液、吸液切换过程4个腔压力分布Fig.6 Pressure distributions when No.1 and No.3 displacement chamber were switched from discharge to suction

2.3 叶轮边缘对差速泵驱动系统转矩影响

图5、6压力分布显示，差速泵的叶轮顶部边缘对腔内流场有明显影响，原有叶轮设计容易形成进出口和腔内压力突变，形成水锤效应，造成流体冲击。为进一步说明叶轮边缘优化有利于减少水锤效应造成的冲击，在Workbench平台中构建流体域和驱动系统的流固耦合分析模型，仿真计算叶轮顶部边缘变化对驱动轴转矩的影响。叶轮1、2优化前后流场对输入轴的耦合转矩如图7所示。

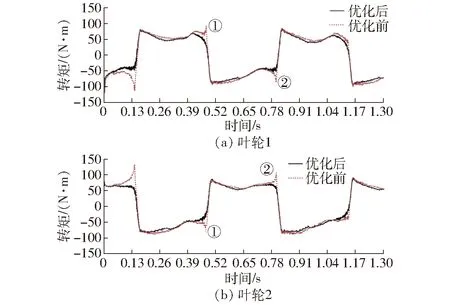
图7 优化前后输入轴仿真转矩比较Fig.7 Comparisons of simulation torque of input shaft before and after optimization

为便于分析比较，工况位置①、②对照图5、6吸排交替工况，差速泵在工况①位置，叶轮1优化前仿真转矩峰值为92.32 N·m，优化后的仿真转矩峰值为72.40 N·m，转矩峰值下降21.58%。叶轮2优化前的仿真转矩峰值为-85.41 N·m，优化后的仿真转矩峰值为-52.64 N·m，转矩峰值下降38.37%。差速泵在工况②位置，叶轮1优化前的仿真转矩峰值为-87.02 N·m，优化后的仿真转矩峰值为-49.28 N·m，转矩峰值下降43.37%。叶轮2优化前的仿真转矩峰值为104.13 N·m，优化后的仿真转矩峰值为71.39 N·m，转矩峰值下降31.44%。如表1所示，优化后差速泵工况交替位置转矩峰值下降明显，该结果说明叶片顶部边缘的优化有利于减少差速泵水锤效应，叶片边缘优化后差速泵腔内流体对传动系统的周期性冲击明显减少。

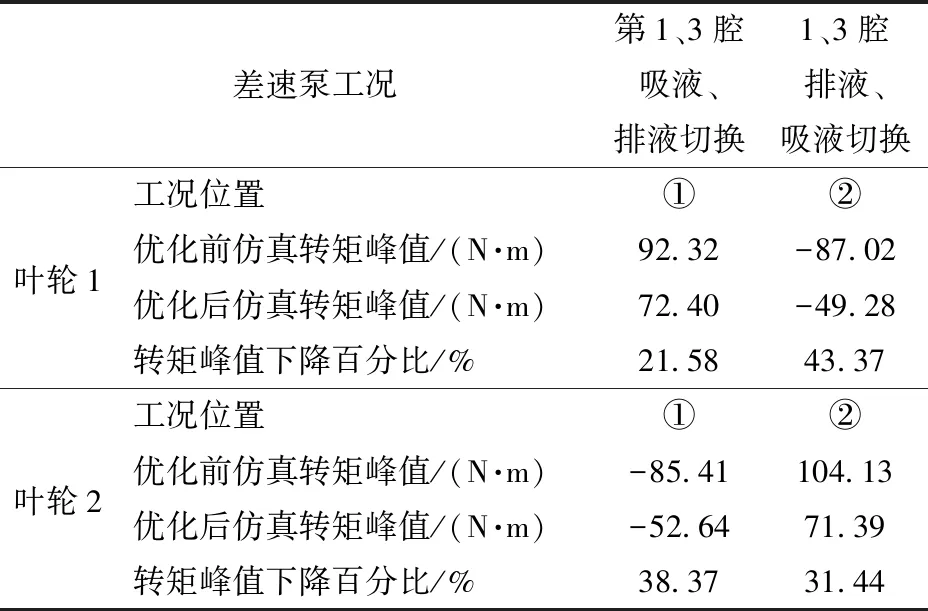
表1 差速泵吸排交替工况与转矩峰值对比关系Tab.1 Contrastive relationship between suction and exhaust alternating conditions and peak torque of differential pump

3 不同叶轮边缘的转矩特性试验

为证实仿真结果，在试验台上进行叶轮边缘优化前后的转矩特性试验研究。试验台架的动力驱动为5.5 kW的电机，通过变频器进行调速控制，变频器设定输入轴转速为90 r/min，电机和差速泵之间安装转速测量传感器、扭矩仪，在差速泵输入轴安装应变片和数据采集及信号发射器等装置，试验用差速泵台架如图8、9所示。

图8 差速泵转矩特性试验台Fig.8 Test-bed for torque characteristics of differential pump

图9 差速泵试验用叶轮的叶片Fig.9 Blades of impellers for differential pump test

选用必创科技TQ201型无线传感器，分辨率为16 bit，使用BUTTERWORTH型抗混叠滤波器，同步精度1 ms，选用BE120-3AA型铂式电阻应变片，测量精度为0.1级，配套的软件为Beedata软件，该测试系统的最高采样频率为500 Hz，进行触发采集。运用惠斯通全桥应变片连接方式，分别接入无线传感器Vexc、Gnd、Sens、S+和S-。为了抵消温变影响，应变片的敏感栅方向和轴方向是45°和135°，如图10所示。

图10 无线传感器和应变片的安装位置Fig.10 Installation location of wireless sensor and strain gauge

把传感器节点、电池和应变片固定在差速泵的输入轴上，直接测量差速泵输入轴的微应变，将数据实时无线传输到网关，实时记录轴的微应变变化规律，再通过转矩和应变的关系计算得到转矩。试验台分别测试叶轮1和叶轮2边缘优化前后的转矩，实测转矩如图11所示。

图11 优化前、后输入轴转矩实测值对比Fig.11 Comparison of measured torque of input shaft before and after optimization

图11所示的工况位置①、②，叶轮1在优化前，输入轴转矩在容积腔工况交替时，存在明显的转矩突变现象，由于水锤效应引起的转矩峰值可达正常转矩的5倍以上。叶轮2在优化前，在容积腔工况交替时转矩峰值可达正常转矩的7倍以上。实测数据显示叶轮1和叶轮2存在转矩差异，主要由于输入轴(轴套和轴)的设计及叶轮安装方式不同，因此在瞬态冲击上有差异，但是不影响转矩突变现象的揭示。叶轮1、2在优化后，转矩突变得到明显的改善，转矩峰值可降低到正常转矩的1.5倍以下，实测转矩结果说明，叶轮边缘优化对改善差速泵水锤效应，减少差速泵周期性冲击具有明显作用。

根据表2可知，叶轮1、2在优化前，转矩的仿真值和试验值差异较大，最大转矩试验值是仿真值的3倍，转矩最大变化幅度是仿真值的2倍。主要原因是叶轮在优化前，差速泵存在明显的水锤效应，造成腔内流体对叶轮的激振力，引起非圆齿轮传动系统严重的扭振冲击，增加了转矩峰值。此外差速泵在实际制造及安装过程中，制造及装配误差会造成非圆齿轮副的齿侧间隙，键与键槽的间隙，变速旋转中会增加额外冲击力。但是转矩的试验值和仿真值随工况变化趋势是一致的，转矩方差较为接近。叶轮1、2在优化后，差速泵水锤效应明显减弱，传动系统的扭振冲击减少，2个叶轮优化后转矩最大变化幅度平均降低51.20%，转矩的试验值和仿真值比较接近，转矩最大值是仿真值的1.5倍左右，转矩最小值是仿真值的1.2倍左右，转矩试验值比仿真值略高，这是因为理论计算时将各运动部件作为纯刚体处理，而在实际运转时，各部件会发生一定程度的变形，在转矩正负交替作用下，传动系统将产生扭振冲击，因此测试值相比仿真值略高一些。从转矩交替规律和峰值转矩出现位置看，仿真结果与实际试验结果基本吻合，差速泵的数值计算结果是可信的。

表2 边缘优化前后输入轴转矩仿真和试验结果特征值比较Tab.2 Comparisons of torque characteristics of input shaft before and after edge optimization of impellers

4 结论

(1)建立了差速泵数值计算模型，利用Workbench平台进行差速泵和非圆齿轮传动系统的流固耦合仿真，分析差速泵不同叶轮边缘对差速泵水锤效应影响，从仿真结果看，叶轮顶部边缘的优化有利于降低差速泵水锤效应，腔内流体对传动系统的周期性冲击峰值至少降低21.58%。

(2)为验证仿真结果，搭建差速泵转矩特性试验台，运用惠斯通全桥应变片连接和无线传感器及网关技术，采集差速泵输入轴和轴套的转矩变化规律。

(3)试验结果显示，转矩仿真值和试验值随工况变化趋势及突变出现的时间点一致，验证了数值计算分析方法的正确性。叶轮边缘优化后，测试转矩最大变化幅度平均降低51.20%，表明叶轮顶部边缘优化有利于差速泵进一步减弱水锤效应，可为优化差速泵结构、减振降噪提供方法。