6-UPS并联机器人快速正向运动学研究
2019-04-29刘艳梨吴洪涛王若冰徐媛媛
刘艳梨 吴洪涛 李 耀 王若冰 徐媛媛 陈 柏
(1.南京航空航天大学机电学院, 南京 210016; 2.江苏安全技术职业学院机械工程系, 徐州 221011;3.南通理工学院机械工程学院, 南通 226002)
0 引言
现有的求解6-UPS并联机器人正向运动学方法[1]可概括为多项式、添加传感器、数值迭代3类方法,这些方法不具备实时反馈的能力。多项式方法可以通过采用对偶四元数方法[2]、特殊的几何性质[3]、Gröbner基算法[4-5]、区间分析[6]和代数消元[7-8]等方法求解非线性方程组,化简得到一元40、20、17、14次的代数方程,最终得到所有可能解,包括无理复根和增根的所有解,运动学正解多解对应多种装配模式,且计算时间长,给实时反馈控制带来困难。文献[9]采用方位特征集方法得到了全解析算法,解决了多解容易产生增根、出现失根问题。传感器方法通过添加4个[10]、3个[11]、2个[12]甚至1个传感器[13-14]来辅助计算正向运动学,能够得到较好结果,但是,添加传感器不但增加了硬件成本,还引入传感器测量误差等问题。文献[13]采用传感器方法得到唯一位姿,但是推导过程繁琐,计算时间较长。数值迭代方法关键是选取一个合适的初始值,如果初值选取得当,使用牛顿-拉夫森迭代方法可以得到唯一解[15-18],否则会影响系统的鲁棒性,同时无法得到所有的装配模式。文献[19]采用四元数得到了正向运动学的快速数值解,消除了姿态矩阵的数学奇异性,是一个较好的数值方法。文献[20]研究了冗余驱动的数值解,消除了算法中位置和姿态的数学奇异性。文献[21]采用齐次坐标变换求解反向运动学。文献[22]采用由点和方位矢量形成的自然坐标法来描述多体系统的位置,而没有使用角度坐标。文献[23]利用链路的自然坐标来描述相邻链路的相对运动,这些自然坐标仅描述机构与所选择的相对系统之间的关系,而不管机构的运动学结构。文献[24]通过选择合适的点和方位矢量形成的自然坐标描述多体系统,建立了一个合适的模型。文献[25]提出了用自然坐标表示的致动器的驱动力公式。采用自然坐标方法描述系统运动学,可有利于建立二次或线性的运动学方程组,能避免三角函数等超越函数计算。
本文将并联机器人运动参数选为若干点的坐标,选择平面平台型6-UPS并联机器人动平台平面中2个动坐标轴端点和坐标轴原点为代表点,将并联机器人运动学表示为3个代表点坐标的函数形式,建立9个一次和二次多项式方程,进行消元处理,得到6个二次多项式方程,在此基础上,改进牛顿-拉夫森迭代算法,最终求解得到唯一一组位置和姿态参数。
1 6-UPS并联机器人运动学基础
1.1 结构
6-UPS并联机器人及其坐标系如图1所示。该机构包括动、静上下2个平台和6条结构一致支腿组成,各个支腿和动平台之间通过球铰S连接,和静平台之间通过虎克铰U连接,支腿上有移动副P,通过对P施加驱动,来保证整个平台的期望运动。该机构属于平面平台型,即动、静平台的6个球铰S和6个虎克铰U中心分别布置在两个平面之中。为了方便分析,选择绝对静坐标系Obxyz与静平台固连,相对动坐标系Oaαβγ与动平台固连,其中,Oa、Ob分别是动、静平台的外接圆圆心;z、γ轴分别垂直于各自所在平面。动、静平台6对顶点Ai、Bi(i=1,2,…,6)分别循环对称布置在一个平面圆周上,如图2所示。

图1 6-UPS并联机器人简图Fig.1 Structure diagram of 6-UPS parallel robot

图2 6-UPS并联机器人的顶点布置示意图Fig.2 Vertices arrangement schematic of 6-UPS parallel robot
选择3点P1、P2、P3为代表点,分别位于动坐标系原点Oa、α轴端点和β轴的端点处,如图1所示。用P1=(x1,y1,z1)T、P2=(x2,y2,z2)T、P3=(x3,y3,z3)T分别表示3个代表点P1、P2、P3在静坐标系Obxyz中的位置坐标,于是正向运动学模型中含有9个待求变量。
1.2 基于代表点坐标的位置P和姿态R
P2、P3和P1存在如下关系:P2=P1+R·x,P3=P1+R·y。动平台动坐标系Oaαβγ的α、β、γ轴对应的矢量记为:α=(αx,αy,αz)T,β=(βx,βy,βz)T,γ=(γx,γy,γz)T。则矢量α、β、γ用代表点P1、P2、P3坐标表示后可得
α=P2-P1=(x2,y2,z2)T-(x1,y1,z1)T= ((x2-x1),(y2-y1),(z2-z1))T
(1)
同理可得
β=((x3-x1),(y3-y1),(z3-z1))T
(2)
由于γ垂直于α和β所决定的平面,所以存在
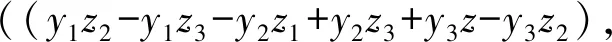
(3)
静坐标系基矢量为:x=(1,0,0)T;y=(0,1,0)T;z=(0,0,1)T。采用代表点表示,动平台位置在静坐标系中的位置矢量为P=P1=(x1,y1,z1)T;姿态矩阵R表示为
(4)
根据式(1)~(3)可得αx=x2-x1、αy=y2-y1、αz=z2-z1、βx=x3-x1、βy=y3-y1、βz=z3-z1、γx=y1z2-y1z3-y2z1+y2z3+y3z1-y3z2、γy=-x1z2+x1z3+x2z1-x2z3-x3z1+x3z2、γz=x1y2-x1y3-x2y1+x2y3+x3y1-x3y2。
2 6-UPS并联机器人位置矢量方程构建
Lkek=P+Rak-bk(k=1,2,…,6)
(5)
其中
ak=(akα,akβ,akγ)T
bk=(bkx,bky,bkz)T
式中Lk——第k个连杆杆长
ek——第k个连杆单位矢量
ak——动坐标系Oaαβγ中动平台各个顶点Ak坐标值
bk——静坐标系Obxyz中静平台各个顶点Bk坐标值
图1所示机构,因动、静平台均为平面布置,所以ak、bk的γ轴和z轴分量均为0,即akγ=bkz=0,也即ak=(akα,akβ,0)T,bk=(bkx,bky,0)T,可见动、静平台的顶点坐标也可以通过4个变量ra、rb、θa、θb来表示,各点坐标进一步表示如下
(6)
其中
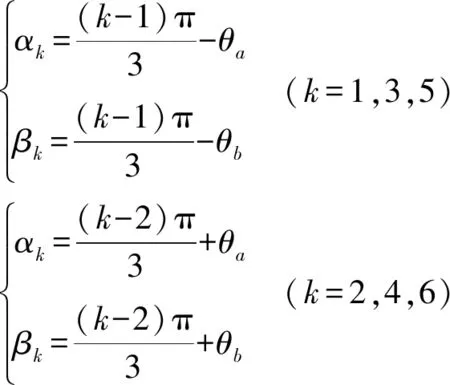
令W为动平台在动坐标系中的位置矢量,W=(Wx,Wy,Wz)T,则存在P=RW,结合R的正交性,同时成立:W=RTP。将ak、bk、P、R和W代入式(5),两边与自身进行矢量点乘,得到6个杆长平方标量方程式如下(此处省略下标k)

(7)
其中Px=P·xPy=P·yWx=P·αWy=P·β
αx=α·xαy=α·yβx=β·xβy=β·y
式中Pp——位置矢量P模长平方
Px——P在x方向上的投影
Py——P在y方向上的投影
Wx——P在α方向上的投影
Wy——P在β方向上的投影
αx——α在x方向上的投影
αy——α在y方向上的投影
βx——β在x方向上的投影
βy——β在y方向上的投影
式中,含Pp、Px、Py、Wx、Wy、αx、αy、βx、βy等9个未知数,各个未知数之间由动平台的位置和姿态各个参数联系起来,且9个未知数的系数由平台结构参数和杆长参数决定。
3 正向运动学模型构造并求解
正向运动学问题就是已知机构的6个杆长输入,求解末端运动平台的位置矢量P和姿态矩阵R。此处首先将正向运动学问题转换为构造和求解6个二次多项式方程问题。
3.1 运动学模型构造
由式(7)可得,通过对Pp、Px、Py、Wx、Wy、αx、αy、βx、βy9个未知数进行移项、整理,可解得
(8)
其中
(9)
将9个未知数的代表点表达式代入式(8)后可得6个一次或二次多项式方程组
(10)
(11)
(12)
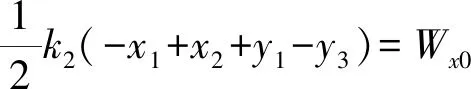
(13)

(14)
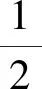
(15)
又由α和β的正交性和归一性
α·β=0α·α=1β·β=1
可得9个未知数的代表点约束方程
(x2-x1)(x3-x1)+(y2-y1)(y3-y1)+ (z2-z1)(z3-z1)=0
(16)
(x2-x1)2+(y2-y1)2+(z2-z1)2=1
(17)
(x3-x1)2+(y3-y1)2+(z3-z1)2=1
(18)
观察式(11)、(12)、(15)最高次为一次多项式,本文先求出x3、y2、y3对x1、y1、z1、x2、z2、z3的线性表示,再代回剩余的6个方程,可得到式(10)、(13)、(14)、(16)~(18)的6个二次多项式方程,将其记为

(19)
其中X为待求未知数,X=(x1,y1,z1,x2,z2,z3),Ci是由6-UPS并联机器人结构参数和6条支腿长决定;Mi由6-UPS并联机器人结构参数所决定;Qi(i=1,2,…,6)是二次项系数矩阵,是由系统结构参数中3个参数ra、θa、θb所决定的6×6维对称矩阵,Qi的具体形式为

将式(19)代表的6个方程统一表示为向量形式
(20)
其中F(X)=(f1(X),f2(X),…,f6(X))T
Q=(Q1,Q2,…,Q6)TM=(M1,M2,…,M6)TC=(C1,C2,…,C6)T
(21)
(22)
3.2 正解运动学方程数值迭代求解
对二次多项式方程组(20)求导,可得
现在考虑牛顿-拉夫森数值迭代算法,当待求未知变量X取第k步数值,即:X=xk时,可得
因此可得
(23)
根据一般牛顿-拉夫森数值迭代算法
(24)
将式(23)代入X=xk时的方程组(20)可得
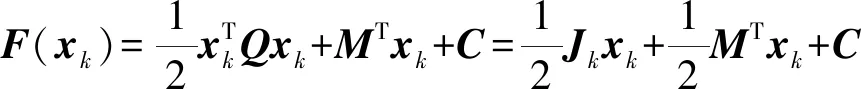
(25)
将式(25)代回式(24)一般牛顿-拉夫森数值迭代算法可得

(26)
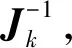
(27)
由式(26)和式(27)联合可得一类代表点表示的6-UPS并联机器人的快速正向运动学迭代算法
(28)
据此,可解出唯一一组变量x1、y1、z1、x2、z2、z3的解,根据P=(x1,y1,z1)T和姿态矩阵R(式(4))可以求解出唯一的位置和姿态。
4 数值算例验证
采用数值算例来说明和验证前文方法的正确性、高效性。
(1)正确性
通过给定一组反解,即给定平台位置姿态,计算对应的代表点坐标值。将给定的一组初始代表点坐标值代入式(28)进行运动学正解计算,如果能够收敛、且收敛到反解对应的代表点坐标值,即可验证所提算法的正确性。
① 给定反解条件。6-UPS并联机器人结构参数θa=0.286 18π、θb=0.046 988π、ra=0.849 864、rb=0.849 864,由此可以确定6-UPS并联机器人动、静平台的顶点坐标ai、bi(i=1,2,…,6)。角度单位为rad,长度单位为m。设定6-UPS并联机器人预设状态下位置矢量为Pt=(-0.2,-0.03,1.1)T,姿态矩阵Rt为
可得到P1=(-0.2,-0.03,1.1)T,通过P2=P1+Rt(1,0,0)T,P3=P1+Rt(0,1,0)T计算可得另外两个代表点坐标分别为:P2=(0.769 017,-0.194 971,1.283 82)T,P3=(-0.028 091 9,0.954 859,1.077 65)T,通过反解计算得到6条支腿长为:L1=1.516 92 m、L2=1.318 95 m、L3=1.268 81 m、L4=1.136 69 m、L5=1.257 04 m、L6=1.209 43 m。
根据课题组研制的物理样机,其构型选择的电缸行程为0.5 m,6条支腿的平衡位置均在1.36 m处,即6条支腿的运动范围均在(1.360.25) m范围内,即:关节空间范围为Li∈[1.11,1.61],i=1,2,…,6,进而可以验证Pt、Rt选取正确。
② 求解正解。首先,将6-UPS并联机器人结构参数和腿长参数代入前述的C、M、Q,可得

假设6-UPS并联机器人动平台从初始位姿:P0=(0.5,0.5,2)T,R0=I3×3出发,运动到反解给定的位姿:Pt、Rt。那么,对应的始末位姿代表点坐标值分别为:X0=(0.5,0.5,2,1.5,2,2)T、Xt=(-0.2,-0.03,1.1,0.769 017,1.283 82,1.077 65)T。
迭代过程如表1所示,经过5次迭代计算后得到的X5=(-0.2,-0.03,1.1,0.769 017,1.283 82,1.077 65)T与反解给定的Xt=(-0.2,-0.03,1.1,0.769 017,1.283 82,1.077 65)T完全一致,验证了所提算法是正确的,机构位姿示意如图3所示。
本次计算中,所提方法迭代时间为0.20 ms,对比计算表明,采用传统欧拉角方法描述的牛顿-拉夫森方法,则迭代次数8次、需要耗时2.67 ms,由此可见本文所提出的二次形方程组数值迭代方法的迭代次数少,用时少,收敛速度快,效率提高92.51%,至此,初步显示出算法的高效性。
(2) 高效性
与旋转矩阵方法的计算进行对比,即可验证所提算法的高效性。所提算法和旋转矩阵方法均在以下条件下进行计算,计算机硬件为:Win 8.1/Intel Core i5 2.4 GHz/8 GB RAM/MatlabR2016b,代表点初始值取X0=(0.5,0.5,2,1.5,2,2)T,最大迭代次数均为20次,算法终止条件允许误差‖Δx‖<10-8。

表1 迭代过程及其结果Tab.1 Iterative process and results

图3 位置和姿态示意图Fig.3 Schematic of position and orientation for 6-UPS parallel robot
为了进一步验证所提算法的高计算效率,根据课题组研制的物理样机,在其可达无奇异工作空间内任意选取25组数据。首先,25组初始位置姿态P0i、R0i均取为P0、R0,其具体数值为:P0=(0.5,0.5,2)T,R0=I3×3,转换成代表点表示为:X0=(0.5,0.5,2,1.5,2,2)T。其次,针对表2中给定的25组数据,其每一组数据均是从初始位姿:P0、R0开始,分别代入所提算法,重复(1)的反解、正解过程并进行计算,动平台最终分别运动到表2中给定的25组终止位置姿态,即25组Pti、Rti处。经过计算可知,25组数据计算结果均正确且收敛,同时也得到每一组数据计算所需时间,并将其与旋转矩阵方法计算反解、正解过程所需时间进行对比。每一组位姿在Matlab中计算100次并取平均数值即为本次计算时间,结果如表2所示。

表2 两种算法计算时间对比Tab.2 Consumption time comparison of two algorithms
5 结论
(1)采用代表点描述可将并联机器人正向运动学模型表达为一组二次方程组。该模型含有二次项、一次项和常数项,最高次项为二次,求导后得到的雅可比矩阵仅含有一次项和常数项,最高次项为一次,建立了简单非线性的并联机器人正向运动学模型。
(2)结合正运动学模型的特点,对一般的牛顿-拉夫森方法进行改进,改进后的牛顿-拉夫森迭代方法不需要求解雅可比的逆矩阵;而且,在每一次迭代计算过程中,部分变量还原到原始二次形,计算过程中直接抵消了大部分计算,方程组与雅可比矩阵的更新仅需消耗极少的计算量,由此确保所提算法收敛速度快、计算效率高,并可得到唯一解,便于实时控制所需。
(3)通过对比传统的旋转矩阵方法,本文提出的二次方程组数值迭代方法的迭代次数少、用时少、收敛速度快,效率高。
