机压微灌管网系统布置与管径同步优化设计

马朋辉 刘韩生 胡亚瑾

(西北农林科技大学水利与建筑工程学院， 陕西杨凌 712100)

0 引言

管网优化包括优化布置和优化设计。优化布置主要进行管网干支管线的选择，力求管网总长度最短或总投资最小的最佳管网结构形式。优化设计则是以管网布置形式为依据，通过水力计算寻求系统造价最低的最佳管径组合方案。

优化布置是优化设计的前提和基础，布置形式合理与否直接影响管道总长度及工程投资的经济合理性，国内外学者对此进行了大量研究[1-8]。相较于优化布置，优化设计对整个系统投资影响较大，所产生的经济效益也较显著。国内外学者对管网优化设计研究非常重视，取得的研究成果也较多。线性规划法[9]、非线性规划法[10]、动态规划法[11]等传统方法，以及近年来发展起来的遗传算法[12]、人工神经网络[13]、蚁群算法[8]等新型智能算法先后被应用于解决管网优化设计问题，极大促进了管网输水技术的应用与推广。

近年来，极端气候频发，水资源供需矛盾日益突出。随着经济的发展，中国工业和城市用水将进一步增加，农业水资源不足的矛盾将更加突出，发展节水灌溉尤其是微灌显得尤为重要。在进行地面坡度较为均匀的大型灌区微灌管网系统优化过程中，当采用井水作为灌溉水源时，可以出水量控制其规模；当采用河水、库水等作为灌溉水源且水量充足时，对于一个待规划的地块，可以将其规划为一个大系统，也可以将其规划为若干个独立的小系统，系统中各级管道的相对长度不同又可以组成多种规划方案，目前多是根据工程经验人为确定单个系统的控制面积，缺乏经济分析。因此，需要确定合理的单个系统的形状、控制面积并进行优化设计，此时微灌管网系统的布置未定，系统中各需水节点的位置及流量也尚不确定。上述的管网优化布置研究[4-8]均是基于各需水节点位置及流量已定的情况，而管网优化设计[9-13]也均为灌溉面积及管网布置已定的情况，显然前述优化方法及模型对大型灌区微灌独立管网系统的优化并不适用。本文以灌区微灌管网系统布置和管径组合的同步优化为研究目标，建立轮灌管网及续灌管网的优化数学模型，通过遗传算法求解，同时获得相应管网的布置及管径组合方案。

1 微灌管网系统优化总思路

微灌管网系统一般由干管、分干管、支管及毛管组成，其中干管及分干管一般采用续灌的方式，组成续灌管网，支管及毛管一般采用轮灌的方式，组成轮灌管网。机压微灌管网系统示意图见图1。目前微灌管网优化方面的研究成果大多仅涉及到某一级管道或轮灌管网的优化，而对微灌管网系统的优化设计问题研究不够[14-19]。实际上，微灌各级管道间有密切的水力联系，各级管道的投资大小也相互影响，在优化过程中，应将微灌管网系统作为一个整体，寻求整个管网系统的最优方案。机压微灌管网系统的优化可以按照一定的顺序进行，即先进行轮灌管网的优化，确定出轮灌管网的形状、面积后，再以此为基础从系统中只有一个轮灌管网到横向、竖向各有多个轮灌管网进行优化计算，以此进行机压微灌管网系统的优化设计。

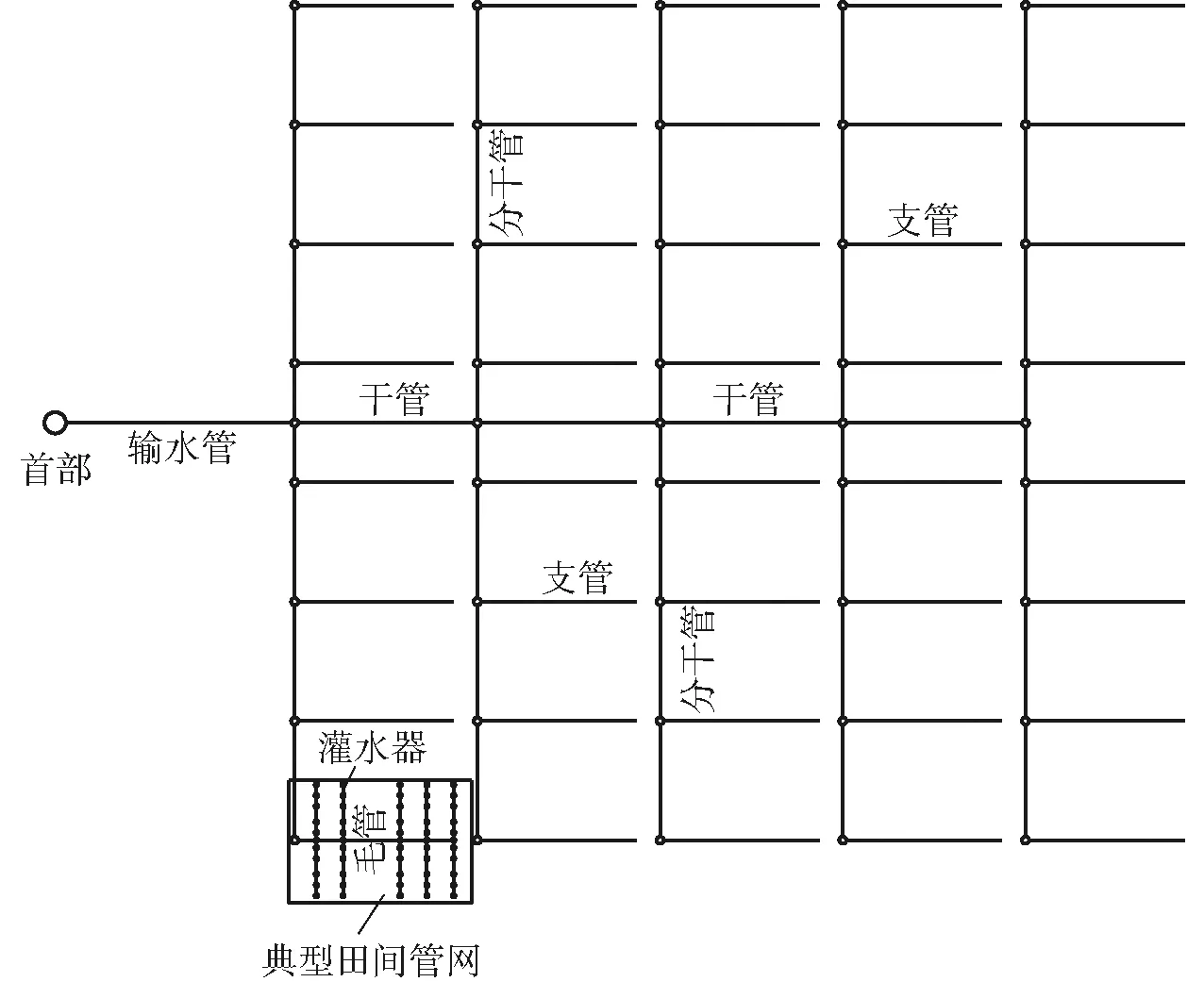
图1 机压微灌管网系统示意图Fig.1 Schematic of pumping micro-irrigation pipe network system

轮灌管网进口压力水头大，所需的动力费用高，但管网内所允许的水头损失大，因此支毛管可以选用较小的管径以节省投资；反之亦然。毛管的规格型号根据作物、土壤性质、农业技术及管理等因素选定，可以作为已知因素，因此轮灌管网优化的目的是在不限定轮灌管网面积的情况下确定使轮灌管网单位面积年费用最小的管网布置形式(面积及支、毛管管长)、支管管径及轮灌管网进口压力水头。在轮灌管网的优化中，假定支管和毛管等量出流，以轮灌管网内各灌水器的工作压力水头在满足灌水均匀度要求所允许的压力水头范围内作为约束条件，以保证灌水质量。

机压微灌续灌管网中,水泵加压所需动力费、管网投资与轮灌管网相同，为此消彼长的关系。因此机压微灌续灌管网优化一方面要降低管网投资，另一方面又要降低管网的动力费用，优化的目的主要是寻求管网年费用最低的优化方案。在轮灌管网优化完成后，续灌管网中各管段的流量就可以确定。以轮灌管网优化结果为基础，在不限定续灌管网控制面积的情况下从系统中只有一个轮灌管网到横向、竖向各有多个轮灌管网进行经济分析，从而确定单位面积年费用最低时续灌管网的控制面积、干管及分干管的管径、管长。将轮灌管网和续灌管网优化结果相结合即为机压微灌管网系统的优化。

在管网水力计算过程中，管道沿程水头损失按《微灌工程技术规范》[20]推荐公式进行计算，即

(1)

式中hf——管道沿程水头损失，m

Qi——管道流量，L/h

Di——管道内径，mm

Li——管道长度，m

f——摩阻系数m——流量指数

b——管径指数

各种管材水头损失计算系数参见《微灌工程技术规范》[20]。支、毛管按微灌用聚乙烯管管径大于8 mm的情况取值，干管及分干管按硬塑料管的情况取值。

2 机压微灌管网系统优化模型

2.1 轮灌管网优化模型

以不设调压管且毛管双向布置的轮灌管网为研究对象，其优化包括布置优化和管径优化。布置优化主要是确定轮灌管网的控制面积，支、毛管的长度及支管位置；管径优化主要是确定支管的管径。规定毛管上2个灌水器之间的管道为一个管段，支管上2条毛管之间的管道为一个管段，毛管不变径且轮灌管网内所有毛管均选用同一规格管径，支管采用变径设计，每一管段只选用一种标准管径。规定顺水流方向左手边为左侧，右手边为右侧，以左侧毛管上灌水器个数、右侧毛管上灌水器个数、支管各管段管径及轮灌管网进口压力水头为决策变量，以轮灌管网单位面积年费用最低为目标函数建立轮灌管网优化模型，从轮灌管网中支管只有一个管段到多个管段进行优化计算。

2.1.1目标函数

以轮灌管网单位面积年费用最低为目标，计算式为

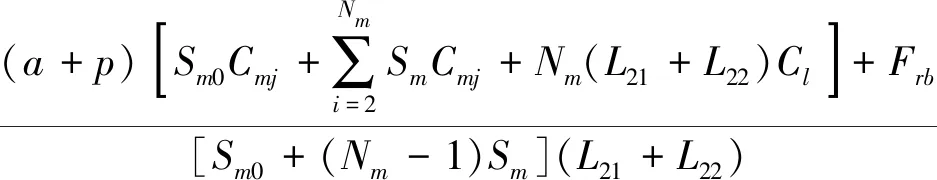
(2)

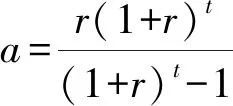
(3)

(4)

L21=Se0+(n1-1)Se

(5)

L22=Se0+(n2-1)Se

(6)

式中Fr——轮灌管网单位面积年费用，元/(hm2·a)

a——投资年折算系数

p——年平均维修费率

Sm0——支管第一管段的长度，m

Sm——支管其余管段的长度，m

Cmj——支管选用第j种规格管径时的单价，元/m

Cl——选用的毛管单价，元/m

L21——左侧毛管长度，m

L22——右侧毛管长度，m

Frb——轮灌管网水泵年动力费，元/a

Nm——支管管段数

r——年利率，%

t——折旧年限，a

E——电价，元/(kW·h)

Tr——轮灌管网年工作时数，h

Qr0——轮灌管网进口流量，m3/h

Hr0——轮灌管网进口压力水头，m

η——泵站效率

Se0——毛管第一管段的长度，m

Se——毛管其余管段的长度，m

n1——左侧毛管上灌水器的个数，即左侧毛管管段数

n2——右侧毛管上灌水器的个数，即右侧毛管管段数

2.1.2约束条件

(1) 灌水器工作压力约束

以一个轮灌管网中所有灌水器的工作压力水头均在满足灌水均匀度要求所允许的压力水头范围内为约束条件，将轮灌管网作为一个整体优化，有

Hmin≤Hk≤Hmax

(7)

其中

(8)

式中Hk——轮灌管网中第k个灌水器的压力水头，m

Hmin——满足灌水均匀度要求的灌水器允许最小工作压力水头，m

Hmax——满足灌水均匀度要求的灌水器允许最大工作压力水头，m

I1——顺支管方向的地形坡度

I2——顺毛管方向的地形坡度

I(k1)——从支管入口到轮灌管网中第k个灌水器所经过的支管管段数

I(k2)——从支管入口到轮灌管网中第k个灌水器所经过的毛管管段数

α——考虑局部水头损失的加大系数,取1.05

(2) 管径约束

支管顺水流方向前一段管道所选标准管径应不小于后一段管道所选标准管径，即

Di,j≥Di+1,j

(9)

式中Di,j——第i段管道选用第j种标准规格的管径，mm

Di+1,j——第i+1段管道选用第j种标准规格的管径，mm

2.2 续灌管网优化模型

续灌管网优化也包括布置优化和管径优化。布置优化主要是确定续灌管网的控制面积、干管及分干管的长度；管径优化主要是确定在此布置形式及规模下干管及分干管各段的管径。规定干管上相邻分干管之间的管道为一个管段，分干管上相邻支管之间的管道为一个管段，干管及分干管均采用变径设计，每一管段只选用一种标准管径。以水泵扬程、干管及分干管各管段管径为决策变量，以单位面积年费用最低为目标函数，建立机压微灌续灌管网优化模型，从续灌管网中只有一个轮灌管网到横向、竖向各有多个轮灌管网进行优化计算。

2.2.1目标函数

以续灌管网单位面积年费用最低为目标，计算式为

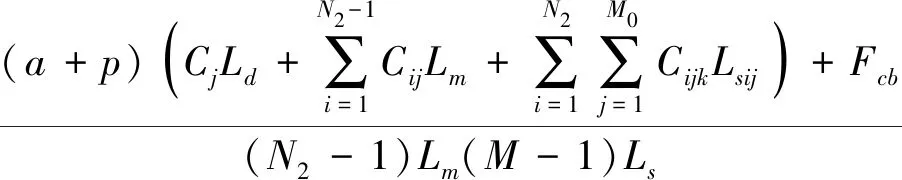
(10)

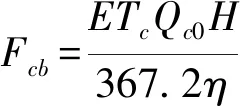
(11)

式中Fc——续灌管网单位面积年费用，元/(hm2·a)

Cj——输水管选用第j种规格标准管径时的单价，元/m

Ld——输水管长度，m

Cij——第i段干管选用第j种规格标准管径时的单价，元/m

N2——干管上分干管的条数，即干管管段数

M——分干管上支管的条数

M0——一条分干管上的管段数，当M为奇数时，M0=M-1；当M为偶数时，M0=M

Cijk——第i条分干管第j管段选用第k种规格标准管径时的单价，元/m

Lsij——第i条分干管第j管段的长度，m

Lm——干管管段长，即相邻分干管间距离，m

Ls——分干管管段长，即相邻支管间距离，m

Fcb——续灌管网水泵年动力费，元/a

Tc——续灌管网年工作时数，h

Qc0——续灌管网进口流量，m3/h

H——水泵扬程，m

2.2.2约束条件

(1) 工作压力约束

续灌管网中分干管各节点压力水头应不低于轮灌管网进口压力水头，即

(12)

式中h1k——续灌管网中分干管各节点最小压力水头约束变量，m

hb——底阀、首部枢纽及吸水管水头损失之和，m

Qd——输水管流量，L/h

Dd——输水管管径，mm

I(k3)——从续灌管网入口到第k个分干管节点所经过的干管管段数

I(k4)——从续灌管网入口到第k个分干管节点所经过的分干管管段数

(2) 管道承压能力约束

续灌管网中各管段的实际压力不大于管道承压能力，即

(13)

式中h2k——续灌管网中分干管各节点最大压力水头约束变量，m

Hc——管道承压能力，MPa

(3) 管径约束

续灌管网中顺水流方向前一段管道所选标准管径应不小于后一段管道所选标准管径，即

Di,j≥Di+1,j

(14)

3 基于遗传算法的模型求解

3.1 编码

轮灌管网优化的决策变量为(D1，D2， …，DN，n1，n2，Hr0)， 共有N+3个决策变量，将D1、D2、…、DN与其管径序号一一对应形成一个有序的整数列，采取整数编码方式，n1、n2为整数，Hr0为实数，对n1、n2采取整数编码方式，对Hr0采取实数编码方式。续灌管网优化的决策变量为(D1，D2，…，DN-1+NM0，Dd，H)，共有N-1+NM0+2个决策变量，将D1、D2、…、DN-1+NM0、Dd与其管径序号一一对应形成一个有序的整数列，采取整数编码方式，对H采取实数编码方式。

3.2 产生初始种群

在遗传算子一定的情况下，初始种群对算法的效率和全局收敛性影响很大，在算子效率难以提高的前提下改进初始种群的产生方法会收到很好的效果[21]。本文采用解的不可行度进行初始种群的选择操作，具体是通过定义一个阈值，当一个解的不可行度大于阈值，则该解被拒绝，否则被接受并进入下一代遗传算法操作。为保证种群规模不变，被拒绝的解由当前代中不可行度最小的解等量取代，具体参见文献[22]。

3.3 适应度函数设计

轮灌管网及续灌管网的优化模型均为带约束优化问题，需先将其转化为无约束优化问题，本文采用罚函数法实现上述转化。对于轮灌管网构造适应度函数

(15)

其中

λ=1/tktk+1=ζtkζ∈(0,1)

式中λ——模拟退火惩罚因子

tk+1——第k+1代退火温度

tk——第k代退火温度，k=0时称为初温

ζ——温度冷却系数

对于续灌管网构造适应度函数

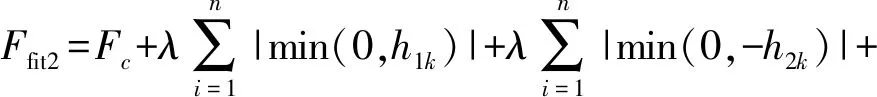
(16)

3.4 遗传算子

(1) 选择算子：首先进行群体中个体适应度的评价，并以此为依据采取排序适应度分配的随机遍历抽样方法，从种群中选取一定比例的个体并作为父辈繁殖子代。

(2) 交叉算子：将种群中的奇数行与它的下一偶数行配对后进行单点交叉，若最后一行为奇数行则此行不参与交叉操作。

(3) 变异算子：以一定概率选择变异的基因位并在该位基因所允许的范围内随机变异。

4 应用

4.1 基本数据

某项目区种植枸杞，土壤容重为1.36 g/cm3,采用膜下滴灌的灌溉方式，水源为河水且充足，干管方向的地形坡度为1/200，分干管方向的地形坡度为1/500。考虑当地气候条件并根据经验选择设计耗水强度为6 mm/d，土壤计划湿润层深度为0.7 m，土壤设计湿润比为50%，田间持水率为25%，适宜土壤含水率上、下限(质量百分比)分别取为田间持水率的90%和70%，灌溉水利用系数为0.9。根据项目区的气候、土壤及作物种植情况选择毛管管径(内径)为16 mm，毛管间距为2.5 m，灌水器设计流量为2.7 L/h，灌水器允许最大工作压力水头为12 m，灌水器允许最小工作压力水头为8 m，灌水器间距为0.5 m。经计算最大净灌水定额为23.8 mm，设计灌水周期为4 d，设计灌水定额为26.67 mm，一次灌水延续时间为11 h，取系统日工作时间为22 h，则系统最大轮灌组数为8，以此进行机压微灌管网系统优化设计。泵站到灌溉区域边界的距离(即输水管长度)为50 m，单座泵站工程投资为20 000元，所选毛管单价为2.0元/m， PE支管单价见文献[19],UPVC干管单价见表1。

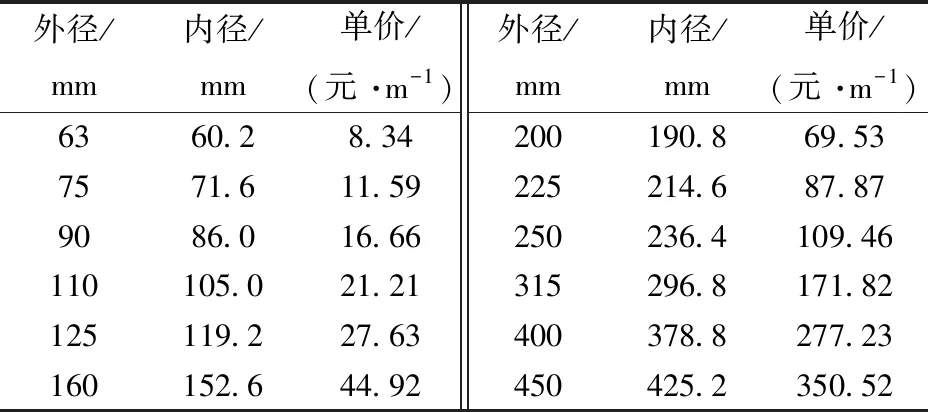
表1 UPVC干管单价Tab.1 Unit price of UPVC main pipes

4.2 控制参数选取

算法中涉及的控制参数较多，其中群体规模和最大遗传代数对计算结果的精度影响较大，对这两个参数进行组合分析以确定合理取值，其余参数均是基于一般情况下的取值。

以群体规模200、最大遗传代数500、交叉概率0.9、变异概率1/NVAR(NVAR为模型中变量个数)为基本遗传参数；以阈值的初始可变因子0.4、最终可变因子1.0、最大迭代次数6为初始种群不可行度选择的基本参数；罚函数法处理约束条件时模拟退火惩罚因子中初温为0.000 01，温度冷却系数为0.99。

4.3 优化结果分析

轮灌管网的优化结果包括控制面积、支毛管管长、支管各管段管径及轮灌管网进口压力水头，具体见表2。

表2 轮灌管网优化计算结果Tab.2 Optimization results of rotational irrigation network

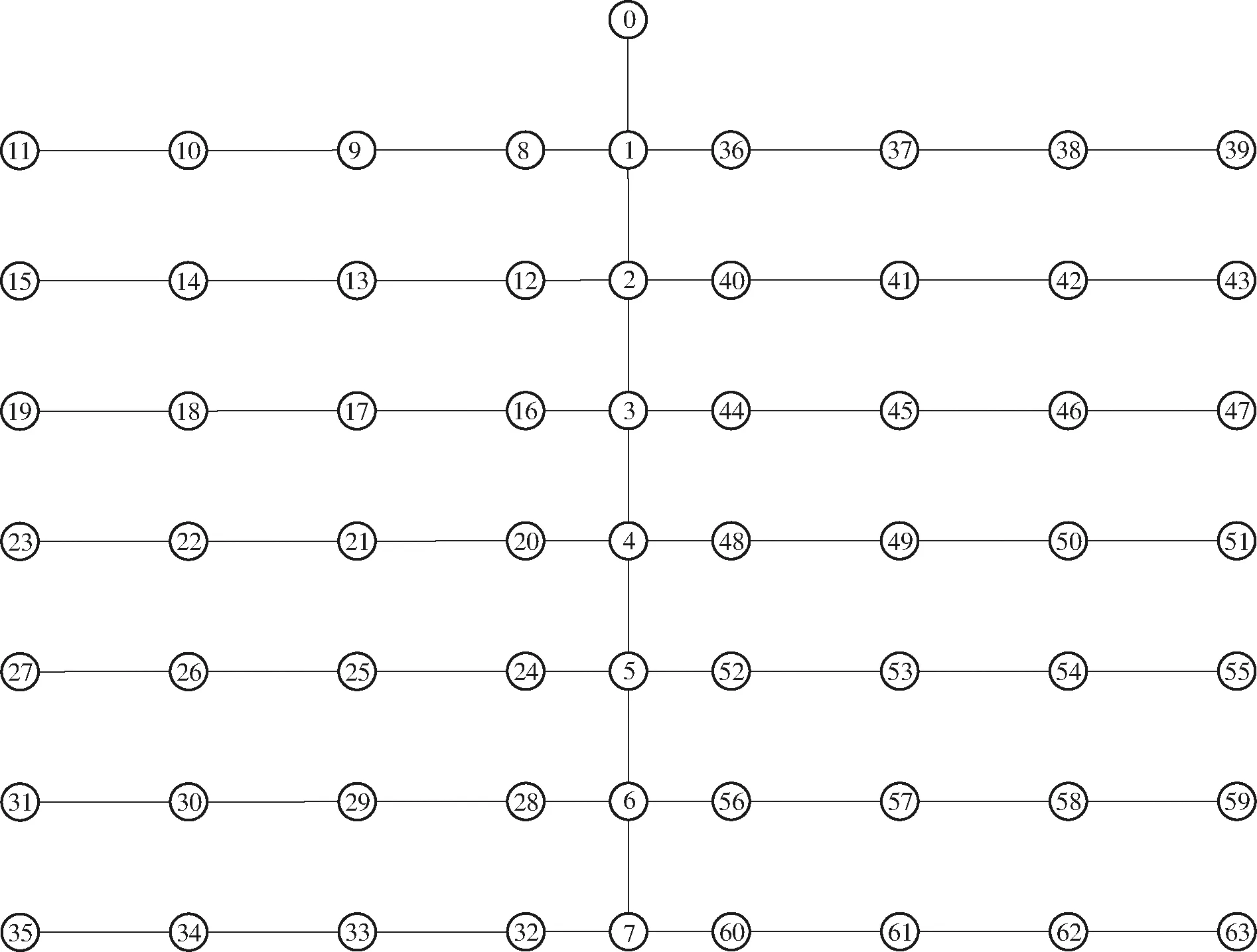
图2 续灌管网优化布置结果Fig.2 Optimization layout results of continuous irrigation network

由于遗传算法采用概率变迁规则指导搜索方向，为克服随机因素对算法求解性能评估的干扰，将算法程序独立运行100次，比较每次运行结果与最优解的相对偏差，结果见表3。本文100次的运行结果中，最优解为1 313.30 元/(hm2·a)，相对偏差小于0.3%的概率达到55%，相对偏差小于0.5%的概率达到81%，相对偏差小于1%的概率达到100%，说明算法收敛性能稳定，具有很高的计算精度。

对微灌管网系统采取干管及分干管续灌、支管轮灌的方式，将分干管上同一位置的支管划分为一个轮灌组。以轮灌管网的优化结果为基础，通过续灌管网优化模型的求解得到优化结果：控制面积为43.89 hm2，单位面积年费用为744.73元/(hm2·a)，干管方向轮灌管网为7个，分干管方向轮灌管网为8个，水泵扬程为34.20 m，系统流量为122.43 m3/h。具体优化布置及优化设计结果分别见图2及表4。

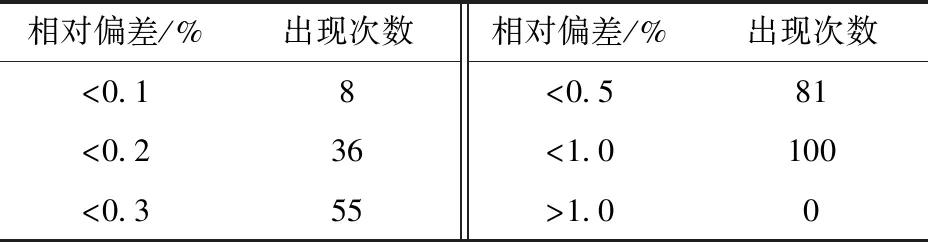
表3 轮灌管网计算结果与最优解相对偏差出现次数Tab.3 Occurrence number of relative deviation between calculation results and optimal solution of rotational irrigation network

同样,为克服随机因素对算法求解性能评估的干扰，将算法程序独立运行100次，比较每次运行结果与最优解的相对偏差，结果见表5。本文100 次的运行结果中，最优解为744.73元/(hm2·a)，相对偏差小于3%的概率达到46%，相对偏差小于5%的概率达到97%，小于10%的概率达到100%，说明收敛性能稳定，计算精度较高，可以满足实际生产要求。

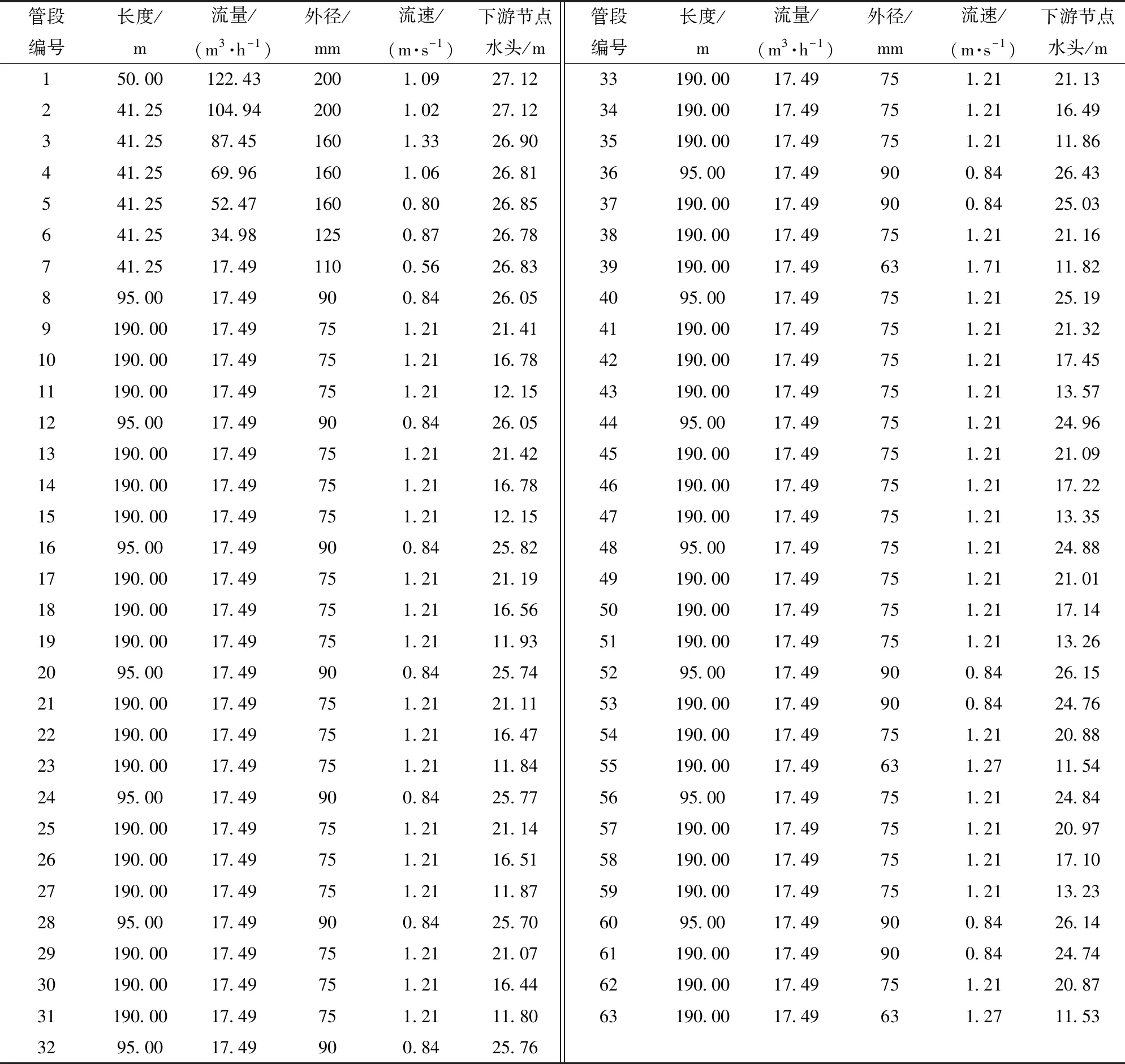
表4 续灌管网优化设计结果Tab.4 Optimization design results of continuous irrigation network

注：管道编号与下游节点编号相同。

表5 续灌管网计算结果与最优解相对偏差出现次数Tab.5 Occurrence number of relative deviation between calculation results and optimal solution of continuous irrigation network

4.4 与传统设计方案的对比

在传统设计中，水源充足情况下续灌管网的控制面积通常是根据经验确定，不限定轮灌管网布置的情况下支管管径也不易选定。以干管方向轮灌管网个数分别为5、7、10，支管管径(外径)分别取63、75、90 mm，进行传统设计并将其结果与前述优化设计结果进行对比。

由于毛管管径根据项目区的气候、土壤及作物种植情况选择，均为16 mm，故各种情况下单位面积年毛管费用均相等，此处单位面积轮灌管网年费用仅考虑不同部分(单位面积年费用为单位面积年支管费用与单位面积年动力费用之和)，轮灌管网优化设计方案与传统设计方案结果的对比见表6。

续灌管网优化设计方案与传统设计方案结果的对比见表7。

轮灌管网优化设计方案与传统设计方案相比，优化部分的单位面积年费用降低了14.85%～

表6 轮灌管网优化设计方案与传统设计方案结果的对比Tab.6 Comparison of results between optimized and traditional design schemes of rotational irrigation network

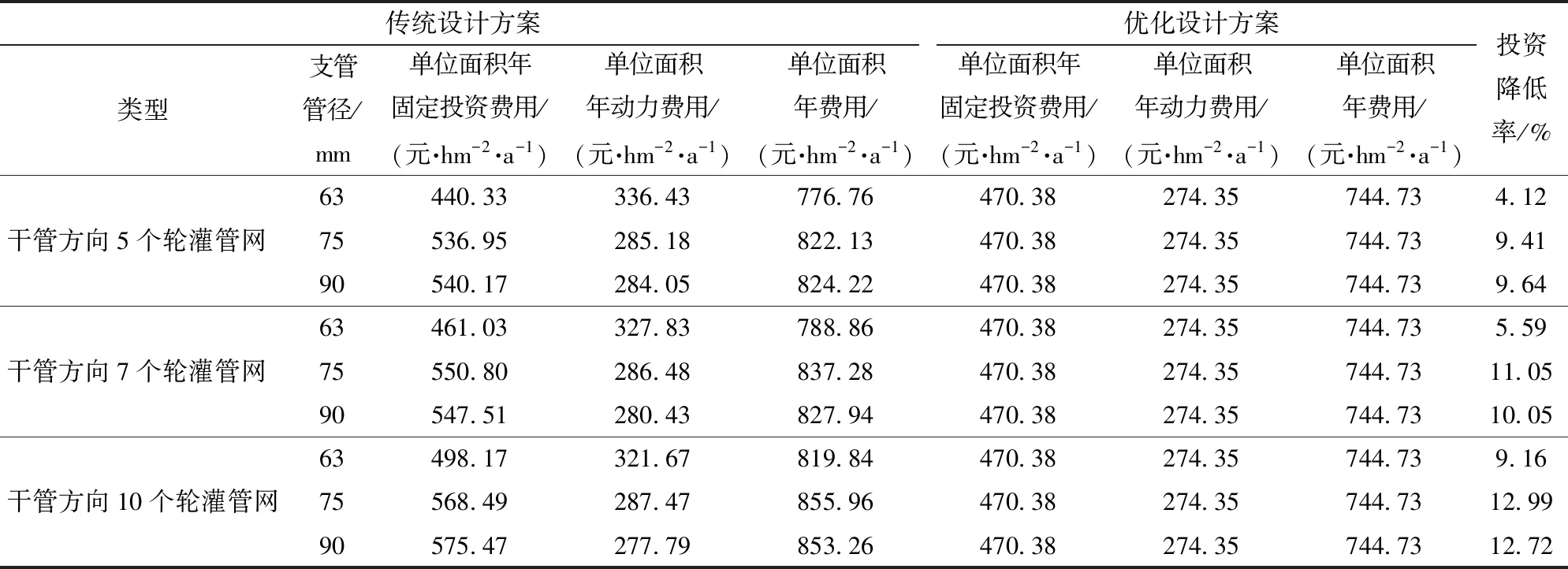
表7 续灌管网优化设计方案与传统设计方案结果的对比Tab.7 Comparison of results between optimized and traditional design schemes of continuous irrigation network

35.59%，续灌管网优化设计方案与传统设计方案相比，单位面积年费用降低了4.12%～12.99%，节省投资效果明显。

5 结论

(1)提出了机压微灌管网系统优化设计方法，即先进行轮灌管网的优化，然后以轮灌管网的优化结果为基础，从一个管网系统中只有一个轮灌管网到横向、竖向各有多个轮灌管网进行优化计算。

(2)建立了机压微灌管网系统优化设计的数学模型，并给出了基于遗传算法的求解方法。将轮灌管网作为一个整体，以单位面积年费用最低为目标函数建立了轮灌管网优化模型，通过求解可以直接得到其布置形式、管径组合方案、控制面积及进口压力水头。以轮灌管网的优化设计结果为基础，以单位面积续灌管网年费用最低为目标函数建立了续灌管网优化模型，通过求解可以得到续灌管网的布置形式、管径组合方案、控制面积及水泵扬程。

(3)采用基于整数和实数的混合编码方法，得出的管径值为标准商用管径，无需调整，避免了圆整化处理对解可行性和最优性的破坏。采用罚函数法处理约束条件，应用遗传算法进行优化计算。实例结果表明，算法收敛性能稳定，具有较高的计算精度。

(4)轮灌管网和续灌管网的优化设计方案与传统设计方案相比较，单位面积年费用分别降低了14.85%～35.59%和4.12%～12.99%，节省投资效果明显。

(5)该研究适用于地面坡度较为均匀、灌溉水源有保证的大型灌区机压微灌管网系统的优化。