TE波在光子晶体中非互易性传播特性研究

余观夏，张晓萌

（南京林业大学 1.理学院应用物理系；2.材料科学与工程学院，江苏南京210037)

光非互易传输器件在光通信系统中具有十分重要的作用，如光二极管[1]、光隔离器[2]、单向吸收器[3]等。实现电磁波非互易性机理之一是通过电磁波在结构的界面激发非互易表面波（surface waves）获得非互易性传播。表面波常见的有3种：第1种是表面等离子体波（Surface Plasmon Polaritons：SPPs），它是在电磁波的激发下，在金属-介质界面上以光子-电子耦合模式沿界面传播的表面电磁波[4]；第2种模式是存在于金属和由光子晶体组成的介质布拉格反射镜（Dielectric Bragg Mirror）界面，在光子晶体的禁带出现的TPPs(Tamm Plasmon Polaritons)[5-6]；第3种表面波模式是存在于两个光子晶体构成的复合结构的界面，在两光子晶体禁带的重合区域出现的OTSs(Optical Tamm States)[7-9]。在外静磁场的作用下，回旋介质（磁光材料）的电磁参数会表现出非对称性，产生非互易性的表面波，导致电磁波传播的非互易性。

虽然3种表面电磁波在一定的条件下都表现出非互易性的特点，但是SPP只能在TE模式下激发，而且激发的结构较为复杂。相对而言，TPPs和OTSs表面波不仅激发的结构较为简单，而且由TM模式和TE模式的电磁波均可以激发[10]。近年在TM模式下激发的TPPs表面波[6,11]和OTSs表面波[12-15]非互易传播的研究受到人们的关注。然而在TE波下由一维光子晶体的复合结构的界面产生的TPPs表面波和OTSs表面波很少有研究。TE和TM波在介质中传播性质不同，激发的表面波也有所不同。在TM波作用下，波的传播特性主要由介质的介电常数起作用，而在TE波作用下，影响电磁波传播性质的主要因素是磁导率。因此有必要研究在TE模式下激发的表面波及其非互易传播特性。

本文构造了由普通介质和旋磁介质周期性交替排列形成一维非对称光子晶体结构，运用传输矩阵法[12]研究其在外静磁场作用下，TE模式激发的电磁波在其中的非互易性传输特性。

1 模型和理论方法

图1所示为非对称的多层光子晶体（AB）N（CD）N结构示意图。N是单元结构的周期数，A和D是普通介质，其相对介电常数分别为εA、εD，相对磁导率为1，厚度分别为dA、dD。B和C分别是加载+y和-y方向静磁场的双轴各向异性旋磁介质，相对介电常数εB=εC=12，其中B和C的相对磁导率可以写成张量的形式：

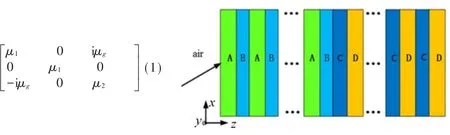
图1 旋磁介质光子晶体结果示意图

式中μ1和μ2为磁性材料张量的主对角元，μg表示由外磁场引起的张量变化，其厚度分别为dB、dC。

设入射电磁波为TE波，入射电场在xoz面内，沿z轴方向以入射角θ入射，电磁波在光子晶体每一层中的场均为透射波与反射波的叠加，因此在光子晶体介质层中传输的电场可以表示为

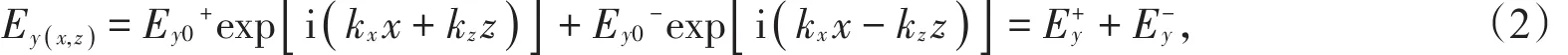
其中‘+’和‘－’分别表示正向波和反射波。不失一般性，假设介质层的磁导率均为（1）式的双轴各向异性的磁回旋介质形式，则分别是x和z方向的波矢分量。由麦克斯韦方程可得磁场的横向分量：

由于电磁波的横向分量在两层介质的界面横向分量连续，用i和j分别表示相邻第i层和第j层介质，由（4）式得到：

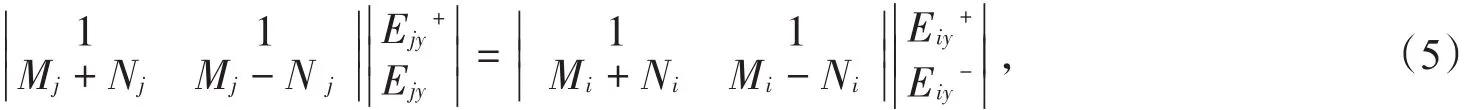
则可获得相邻的第j层和i层中电磁场的横向分量的关系矩阵：

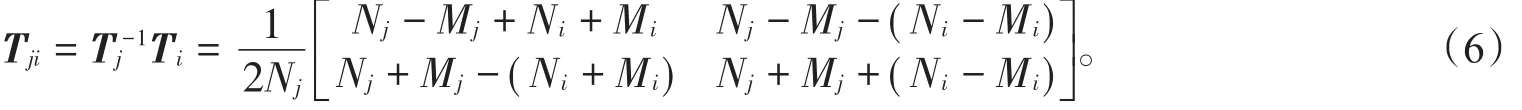
同时考虑在任一厚度为lD的介质层从前到后的相位变化关系为

由此可获得从空气到介质，以及在介质中传播和从介质到空气传播的复合传播矩阵：

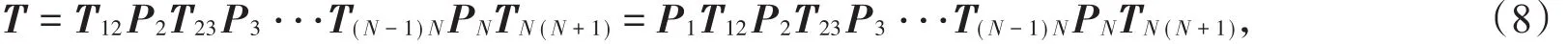
以此可得入射波、反射波和透射波满足如下关系：

由该传播关系可获得电磁波通过多层结构的透射系数t和反射系数r：

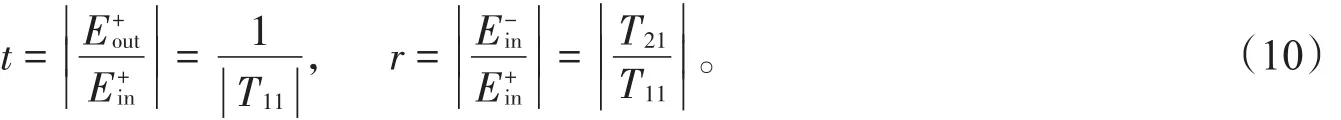
通过透射系数和反射系数的变化规律就可直观反映电磁波在多层介质中的传播规律。

2 数值仿真与分析

采用周期数N=8，A介质取普通的二氧化硅，εA=3.9，D介质是四氮化三硅,εD=6.25，μA=μB=1，dA=140.5 nm，dD=80.4 nm，C和B是两种磁化方向不同的旋磁介质，取常见的旋磁介质铁氧体材料，虽然其电磁参数是频率和外磁场的函数，但在高频情况下，其介电常数趋于常数，取εB=εC=12，相对磁导率趋于1，取μB=μC=1。在高频情况下，旋磁介质回旋磁导率较小，趋于常数，小于1，为增加回旋电磁参数在非互易的作用，取μg=0.4，其厚度分别为dB=120.4nm，dC=145.4nm，取入射电磁波的幅值E0=1。

图2是入射角为30°时分别由正向和反向入射时透射系数和频率的关系，其中虚线代表正向入射，实线代表反向入射。可见，在4.6×1014～4.9×1014Hz禁带区域出现了两个明显分离的频率透射峰，其中正向传输时的透射峰值对应的频率为f1=4.762 0×1014Hz，反向传输时为f2=4.827 6×1014Hz，可见两个复合不对称的光子晶体结构在TE模式电磁波入射时也能实现电磁波的非互易性传播，与一维复合光子晶体在TM模所激发的非互易性一致[13]。

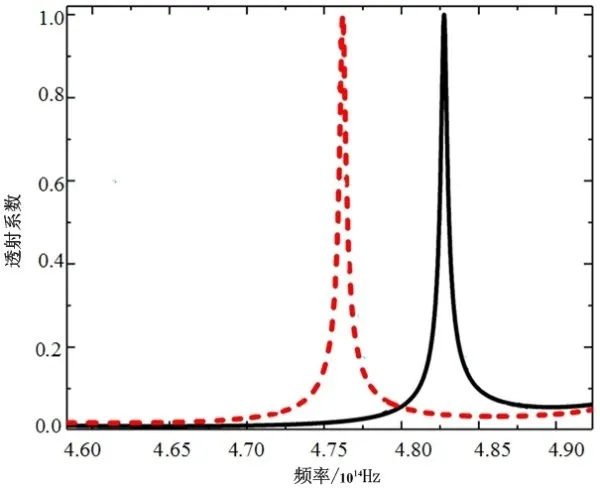
图2 旋磁光子晶体的透射光谱图

TE模式电磁波在两个光子晶体的禁带区域激发了OTSs表面波，不同于金属与普通介质表面激发的表面等离子波。由于等离子波的频率一般大于入射电磁波的频率，需要特定的高介质棱镜或光栅等波矢匹配结构，才能有效激发等离子波[4]。OTSs表面波是在满足光子晶体禁带条件下，特定频率的电磁波以共振的形式存在于两个光子晶体的界面中，在界面加强，随着两侧离开界面的距离增大而减小，使得入射波能够有效地透射。由于外加相反方向的静磁场，破坏了两侧晶体结构中回旋磁介质结构的对称性，即回旋介质电磁参数的非对称性导致了OTSs表面波非对称性，产生正反方向电磁波透射频率不一致的非互易性传播。

不同入射角的电磁波在入射时，沿传播方向会有不同的波矢量，即不同的传播模式，因此入射角也会影响界面表面波的激发。在复合结构中，在其他条件不变的情况下，以入射角分别为π 7，π 6，π 3和π 4的入射角入射，得到其非互易传播特性如图3所示，红色虚线代表正向入射，黑色实线代表反向入射。由图3可以看出，随着入射角的增加，非互易传播仍然存在，但当入射角度增大时，正向和反向的透射峰均出现了蓝移，同时两透射峰峰距增大，正向和反向的非互易性增强。

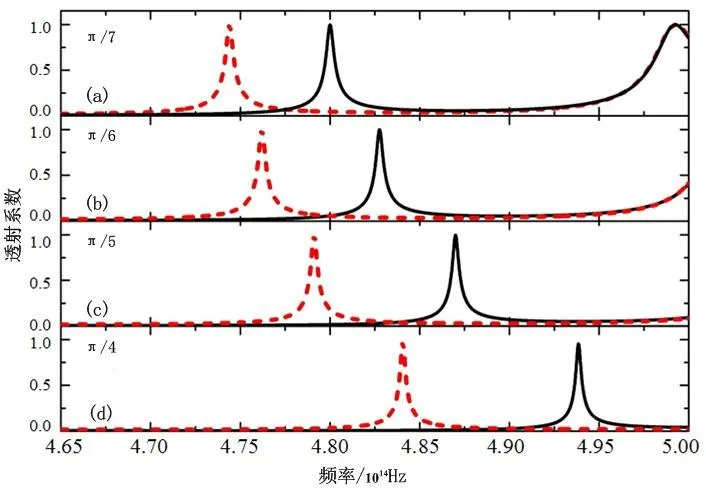
图3 入射角分别为（a）π 7，（b）π 6，(c)π 3和(d)π 4时的透射谱

电磁波在复合光子晶体中的非互易传播取决于光子禁带中界面表面波的激发，在两个光子晶体的界面，OTSs表面波被激发到最大值，沿着界面两侧的光子晶体分别向外衰减[12,15]。因此光子晶体层数的变化对表面波的激发和增强起着重要的作用。在其他条件和图2一致的基础上，改变一维复合光子晶体的周期数N，观察非互易性传播特性。图4描述非互易性透射系数和对应频率的关系，其中实线、短划线和点线分别表示N=7，N=9，N=11。通过观察可以发现，N值越大对应的峰宽越窄，两个峰值分得越开，互异性越强，且随着N值的增大对应峰值频率轻微红移，并趋于稳定。但当复合光子晶体的层数进一步增加时，非互易性的透射峰值会下降，甚至会消失。因此一定层数的光子晶体结构有利于表面波的激发和增强，提高非互易性电磁频率的选择。

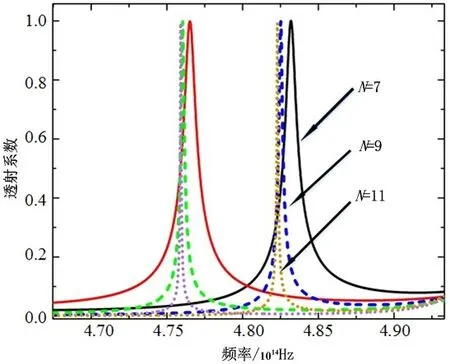
图4 光子晶体周期数N不同时的透射峰

复合光子晶体结构的非互易性传播特性主要基于两侧光子晶体中磁光介质的非对称性电磁参数。在TE模式电磁波的激发下，光子晶体中磁光介质非对称的回旋磁导率是产生非对称性表面波的重要因数。在外静磁场作用、激发频率较高时，随着频率的增大，结构中B和C层磁光介质的回旋磁导率μg趋于减小，将对电磁波的非互易性传播产生影响。图5是不同回旋磁导率时非互易性透射系数和频率的关系，其他条件与图2相同。可以发现，当μg的取值逐渐降低时，非互易性透射频率依然存在，但对应的透射峰位置在稳定地左移，两个透射峰的高度也随μg的降低而降低，同时μg的取值变小，两个峰值的峰距也变小，峰宽变宽，这说明随着磁光介质参数的降低，非互易性的效果减弱。

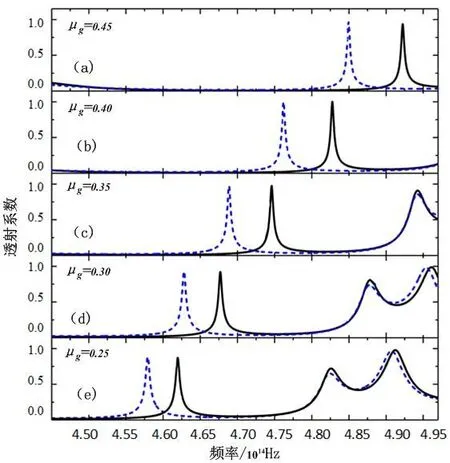
图5 μg的取值对光子晶体非互易性光传输的影响。（a）μg=0.45；（b）μg=0.40；（c）μg=0.35；（d）μg=0.30；（e）μg=0.25

为了进一步直观验证TE模式电磁波的非互易性传播，根据图2的非互易性传播频率，数值仿真了电场在xoz平面的分布图。图6是对应图2中两个互易性频率正向和反向入射时的电场Ex分布图。由图6（a）可以看出，频率f1=4.762 0×1014Hz电磁波正向入射时在两层晶体结构中产生较大OTSs表面波，在两对光子晶体的界面达到最大，电磁波能完全透射；反之，当同频率的电磁波反向入射时，无法在结构中激发OTSs表面波，透射电磁波被抑制，电磁波几乎被完全反射，在入射区反射波和入射波叠加形成完美的驻波。同样对频率f2=4.827 6×1014Hz入射波，在反向入射产生较强的表面波，电磁波能完全透射，而正向入射时被完全反射，如图6（b）所示。

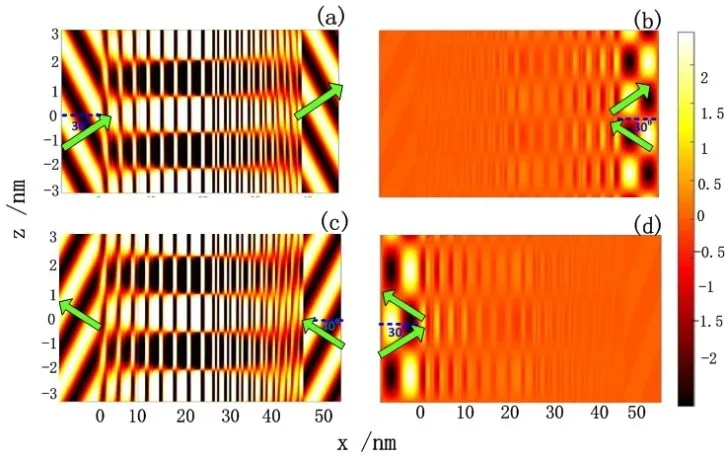
图6 电场Ex分布图。（a）30°正向入射，透射峰f1=4.762 0×1014Hz；（b）30°反向入射，透射峰f1=4.762 0×1014Hz；(c)30°反向入射，透射峰f2=4.827 6×1014Hz；（d）30°正向入射，透射峰f2=4.827 6×1014Hz

3 结论

本文设计了两种分别有由普通介质与旋磁介质交替排列的旋磁光子晶体复合结构，研究了TE模式电磁波激发下电磁波的非互易性传输特性。数值分析了不同的入射角、光子晶体的层数和旋磁介质的回旋磁导率对非互易性传播特性的影响。结果表明，入射角度增大时，结构的非互易性增强；随着回旋磁导率的变小，结构的非互易性效果降低。运用旋磁介质设计的一维复合光子晶体结构，为TE模式激发下的电磁波实现非互易性传输提供了理论和方法，对光通信技术以及集成光路等领域设计光隔离器和光二极管具有实际的参考价值。