正交调制器包络时延测量新方法
2019-04-28陈德明顾卫红王志虎
夏 伟,陈德明,顾卫红,王志虎
(中国卫星海上测控部,江苏 江阴 214431)
0 引言
随着科学技术的不断发展,在航天测控、卫星导航、星间无线电测量等诸多领域中,对距离和远程时间差的测量精度要求越来越高。但由于组成测距系统收发信机的调制器、变频器、功放、低噪放等设备都是非线性相位系统,测距信号经过这些非理想传输信道时会产生群延时波动和相位畸变;同时在实际系统中普遍存在的噪声干扰、多径影响、阻抗失配、温度漂移等不确定误差因素,都将造成测距系统时延零值的波动变化,成为影响测距系统测量准确度的主要误差因素[1-2]。因此,对测距系统收发信机进行经常性的时延零值测量与统计分析,对确保系统测距性能具有重要意义。
1 时延测试原理与面临的问题
1.1 时延测试原理
当信号通过某一传输系统或网络时,其输出信号相对于输入信号总会产生滞后时间,这就是时延。根据传输信号是否为调制信号的不同,系统时延特性可使用相位时延或包络时延来描述[3-4]。由于相位测量具有2π的周期性,所以进行相位时延测量时需考虑相位周期性引起的距离模糊问题。如果通过系统的信号是经过调制后的信号,且调制信号的包络是非恒定的,则系统输出信号的包络相对于输入信号包络所产生的延迟时间称为包络时延。
时延测试的方法可分为载波测量法和调制测量法。文献[1]总结并归纳了载波测量法的基本原理和方法。其中,矢量网络分析仪同时具备系统时延和群时延测量能力,且针对变频系统时延测量亦提供了多种测量解决方案[5-6],主要应用于单元级测量。调制测量法是根据信号时延估计原理,将载波调制后通过被测器件,在输出端对信号进行解调后通过与参考信号比相来估计时延。其中,基于现代扩频通信技术的扩频伪码测距为距离模糊问题提供了解决方法[7-9],主要应用于系统级测量。
本文所述调制器时延即为包络时延测试的典型应用,其测试原理如图1所示。

图1 正交调制器时延测试原理
其中,基带信号发生器用于生成正交(IQ)基带信号,使用功分器把一组IQ信号送入正交调制器进行带通调制。调制器输出信号输入数字示波器测量通道。功分器把另一组IQ信号作为参考信号直接输入数字示波器,通过比较已调制信号包络波形与基带信号波形的时序关系,得到正交调制器的时延特性。文献[10]对调制器发射时延进行了定义:从基带输入伪码跳变沿上升到50%最高均值电平起始,到该跳变沿对应的射频相位翻转点的时间延迟。但在实际测试过程中,使用该定义进行调制器时延测试还存在诸多不确定因素,下面进行简要分析。
1.2 基带输入伪码跳变沿的不确定性
文献[10]把调制器分为两类,即有参考钟输入的调制器和无参考钟输入的调制器。对于有参考钟输入的调制器,由于调制器内部利用输入钟的上升沿对输入测距码重采样后进行调制,因此基带输入伪码跳变沿可定义为从输入钟的采样上升沿到50%最高均值电平位置所对应的时刻。这其中涉及输入钟的上升延、基带伪码跳变沿及对应射频相位翻转点的时序关系。由于输入钟信号是周期重复的,则其与射频相位翻转点之间因周期重复性而产生的“距离模糊”问题将不可避免。对于无参考钟输入的调制器,只能对基带输入伪码跳变沿中点进行人工估计,并加上基带输入伪码信号(包含I、Q两路波形信号)。由于射频相位翻转点位置与I、Q两路信号同时相关,无论以哪一路作为参考,都将引入测量误差。
1.3 射频相位翻转点的不确定性
对于一个理想的PSK调制信号,从理论上说,载波信号应该在调制信号变化时刻相位变化,在调制前和调制后载波信号是等幅的,即包络恒定。但实际测量过程中并不能看到这样的理想波形,而是有一个幅度最小点。这是由于调制器输入IQ信号并非理想矩形脉冲信号引起的。在实际工程应用中,信道带宽总是有限的。这种带限信道的冲激响应在时间上持续无限长,因此一个传输时隙内的理想矩形脉冲信号经过带限信道后将在其它时隙上形成非零值,称为波形的拖尾。这种拖尾波形和其他时隙上的传输波形相互叠加会造成传输符合间干扰,即所谓的码间串扰[11]。因此,为了克服码间串扰,一般基带传输信号都会使用滚升余弦滤波器进行带限预处理。当相位翻转点变换为包络幅度最小点时,由于包络幅度最小点的渐变性导致相位翻转点定位困难。
1.4 测量重复性问题
在利用数字示波器进行调制器时延测试的过程中,由于基带伪码信号和调制输出信号都具有伪随机特性,直接使用示波器测量将无法稳定触发,测量重复性无法保障。文献[12]通过编制计算机软件对示波器测量波形进行实时统计分析,捕获满足条件的相位翻转点,实测该过程操作复杂不便。针对此问题,本文通过试验验证,证明基于Agilent公司的基带信号发生器波形标记技术可以解决此问题。其原理是在基带信号任意采样时隙上通过加注标记符号,使得基带信号发生器在播放基带信号波形序列时,在标记符号有效时间间隔生成一个同步触发信号。其标记间隔最小为基带信号的一个采样时隙。实际测试应用中,通过在基带伪码信号跳变沿设置波形标记,基带信号发生器根据标记位置生成触发信号,数字示波器使用该触发信号可以实现对基带伪码信号和调制信号的重复测量。
2 正交调制器时延估计模型与仿真分析
根据当前正交调制器在时延测试中遇到的问题,以下从正交调制器的调制工作原理出发,通过建立基于最大似然原理的时延估计模型,给出一种正交调制器时延测试新方法。
2.1 正交调制器调制原理分析
数字调制是将数字符号转换成适合信道传输特性的波形的过程。这里的信道一般包括基带传输和射频通带传输两类,因此,数字调制通常也分为基带调制和通带调制两部分。典型正交调制原理如图2所示。

图2 典型正交调制原理图
本文所述正交调制器即数字调制中的通带调制部分。以下依据其工作原理分析其输入输出信号关系,为时延估计作准备。首先利用欧拉三角等式,引入正弦载波信号的复数表示形式,如式(1)所示:
ejω0t=cosω0t+jsinω0t
(1)
调制器输入I、Q信号用复数形式,可以表示为:
g(t)=x(t)+jy(t)
(2)
则由调制器工作原理得输出信号为:
sm(t)=Re]g(t)ejω0t]
(3)
理论证明[13],一个物理可实现的系统,由于因果性的制约,其系统函数的实部和虚部互为一对希尔伯特变换。因此,调制器输出信号的希尔伯特变换可表示为:
(4)
则调制器输出信号的包络可表示为:
(5)
由式(3)、式(4)式可知:
(6)
因此:
z(t)=g(t)ejω0t=g(t)
(7)
由于式(1)中载波信号幅度默认为1,设实际幅度为A,则式(7)修正为:
(8)
2.2 调制器调制仿真分析
以下通过Matlab/Simulink软件对调制器输入输出关系进行仿真验证。试验设计如下,建立基于QPSK调制的仿真模型,观察输入输出信号波形关系。QPSK调制仿真模型如图3所示。
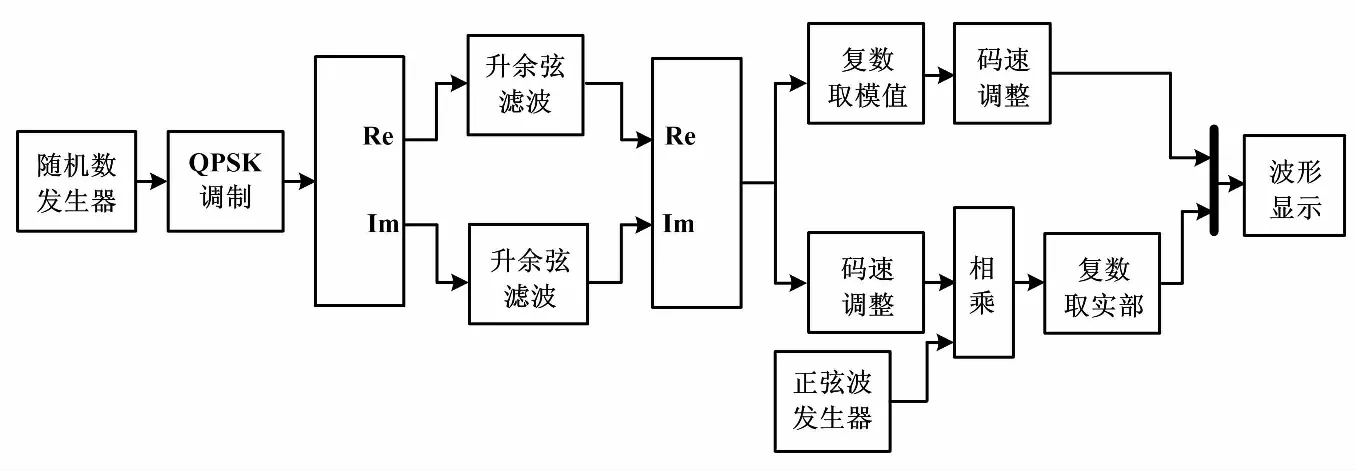
图3 QPSK调制仿真模型
图3中,基带调制使用通信模块库中QPSK Modulator Baseband模块和Raised Cosine Transmit Filter模块生成I、Q基带信号,通带调制基于式(3)所示复信号相乘原理实现,最后使用Scope示波器模块比较通带调制输入输出信号时序关系。QPSK调制输入输出波形如图4所示。
根据图4仿真结果所示,输入复信号的模值波形与输出信号包络波形保持一致,说明式(8)描述的输入输出波形关系是正确的。
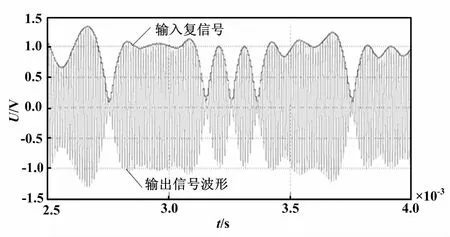
图4 QPSK调制输入输出波形
2.3 调制器的时延估计
下面依据式(8)信号输入输出关系,分析基于最大似然原理的调制器时延估计模型。
为便于推导,令:
(9)
设输入I、Q信号经过调制器时引入时延τ,则输出波形可表示为:
z(t}=r(t-τ)+n(t) 0≤t≤T
(10)
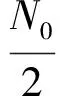
实际测试时使用数字示波器以恒定间隔对输入输出信号波形进行抽样测量,当抽样间隔Δ足够小时(满足奈奎斯特采样定理),可得到离散数据模型:
但是不同于祖母所代表的墨西哥传统女性,赛利亚意识到依靠男性并不能真正使自己摆脱困境,并鼓励女性实现自身价值,这是她不同于墨西哥传统女性的女性觉醒。
z[n]=r[n-nτ]+v[n]n=0,1,…,N-1
(11)
τ=nτΔ
(12)
N为观测周期T内数据采样数,即T=NΔ。因此,本文调制器时延估计可描述如下。通过对输出序列z[n]的N次独立观察测量,求时延参数nτ的最大似然估计。由式(13)知输出采样点z[n]的概率密度函数为:
(13)
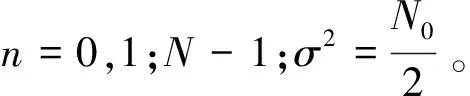
则似然函数可表示为:
(14)
式(14)两边取对数,得对数-似然函数:
(15)
为使式(15)最大,等价于使下式(16)最小:
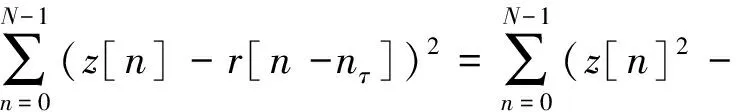
(16)
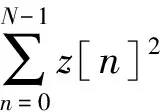
(17)
因此,基于最大似然估计的调制器时延估计求解过程如下:改变延迟参数nτ,当输出信号序列z[n]与输入信号序列r[n-nτ]的相关值最大时,nτ取值即为最大似然估计的解。此时,调制器时延可用式(14)求得。
3 试验验证
为验证本文所述正交调制器时延测试方法的可行性,设计了由基带信号发生器、正交调制器和数字示波器组成的时延测量试验装置,如图5所示。其中,基带信号发生器生成IQ基带信号。其中一组进入正交调制器进行通带调制,另一组作为参考信号直接连接到示波器。正交调制器输出射频调制信号连接到示波器。示波器采集记录相关波形序列用于调制器时延估算。
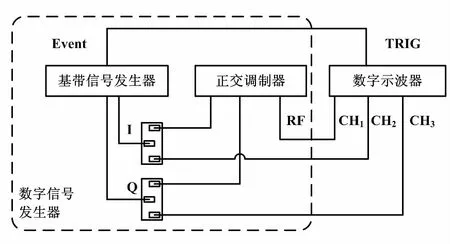
图5 调制器时延测量装置示意图
具体时延估计步骤如下。
①根据式(10)计算IQ输入复信号的模值波形序列。
②对调制器输出信号进行希尔伯特变换,求调制器输出复信号,通过该复信号模值可得调制器RF输出信号的包络波形序列。
③计算IQ复信号和调制器输出复信号相应模值序列的相关性。
④取最大相关时延迟步进nτ代入式(14),计算调制器时延量。
根据示波器实际采样参数,波形记录时间长度为1 μs,采样点数为2 500个,采样间隔为0.4 ns,输入/输出复信号模值最大相关点时延步进数为2 449,则调制器实际时延计算如下:
τ=nτΔ=(2 500-2 449}×0.4ns=20.4ns
(18)
4 结束语
综上所述,传统时延测量方法需要人工判读调制器输入基带信号跳变沿或输出信号包络翻转点位置,导致时延测量存在明显人为读数误差。本文从正交调制器工作原理出发,给出了基于最大似然估计模型的调制器包络时延测试新方法。仿真试验与实测试验结果波形均与理论波形相吻合,表明该方法测量原理准确可靠,时延测量分辨率可达到数字示波器最小时基采样分辨率。
