自动化立体仓库出入库路径优化研究

李媛媛，郑 孟 （兰州交通大学 交通运输学院，甘肃 兰州 730070）

自动化立体仓库系统，是由高层立体货架、堆垛机、输送系统、信息识别系统、计算机控制系统、通信系统、监控系统、管理系统等组成的自动化系统，可持续地检查过期或查找库存的产品，防止不良库存，提高管理水平。

仓库的出入库效率直接影响到整个物流系统的效率，因此出入库路径的优化就成为提高整个物流系统效率的关键问题，出入库通过堆垛机的拣选作业来完成，解决堆垛机行驶路径优化问题是提高自动化仓库运行效益的有效手段。本文根据自动化立体仓库的作业特点建造了数学模型，使用近似动态规划进行了求解,并通过仿真程序证实了算法的有效性。

朱文真[1]、郑欢[2]、刘巍巍[3]等人都曾在自己的文章中针对仓库出入库路径优化问题建立了相关模型并采用相应算法进行求解，求解算法多为遗传算法、禁忌算法、蚁群算法等现代启发式算法，在收敛性、最优解及求解速度上各有千秋。本文针对此问题使用了近似动态规划算法（Approximate Dynamic Programming，ADP） 来进行求解。ADP由美国普林斯顿大学的数学家Powell[4]教授提出，相较于动态规划方法，ADP利用近似结构逼近DP方法中精确计算值函数的过程，可彻底解决动态规划的“维数灾”问题。

1 问题分析

仓库调度优化问题的核心是拣选作业的优化调度问题，拣选作业是由堆垛机来完成的。因此，从本质上来讲，仓库调度实际上就是堆垛机调度。堆垛机是立体仓库中的一种货物输送车辆，能够沿着规定的路线行驶，将货物送到指定的地方。存储货物时，由巷道堆垛机将暂时存在入库台的货物搬运到目的位置；取出货物时，需要堆垛机将货物从存储货架搬运到巷道口，暂时存放在出库台等待后续操作。在实际生产中，仓库的主要作业就是存取作业，任务非常繁重，通过多台堆垛机并行、高速工作以满足拣选任务要求。由于作业任务量大，工作过程复杂，如果对仓库系统调度不合理，就会出现货物拥挤堵塞现象，影响了货物周转率，降低了立体仓库整体工作效率。因此当仓库中有成批货物进行出入库作业时，对仓库系统的调度就显得特别重要。

一批生产任务中，通常包含若干个入库任务和出库任务，堆垛机出入库作业有单一作业（单一入库作业、单一出库作业）和复合作业两种。多数研究表明，复合作业相比起单一作业更有效率[5]，即通过将一个入库任务和出库任务配对执行来提高整体的运行效率。如图1所示，假设O点为堆垛机运行起始点，此时A要进行入库作业，B进行出库作业，若只进行单一作业，则堆垛机行驶的时间t单=2tOA+2tOB，而完成相同的任务，进行复合作业的时间为t复=tOA+tAB+tOB。可以看出，复合作业比单一作业运行时间更少，效率更高。

图1 单一作业与复合作业

通过对复合作业中堆垛机运行情况的观察，每次任务所消耗的时间主要由以下3部分组成[3]：（1）负载运行时间，即堆垛机承载托盘行进所花费的时间（如tOA和tOB）；

（2）空载运行时间，堆垛机在没有承重的情况下行进所花费的时间（如tAB）；

（3）取/放货时间，堆垛机在货架和货台取放托盘时所花费的时间。

在以上3部分中，堆垛机负载运行的时间和取/放货时间都是固定的，所以此路径优化问题是通过对堆垛机的任务队列进行合理排序，减少堆垛机的空载运行时间来降低完成所有任务的总时间。

堆垛机每一次的复合作业可以简化理解为非对称TSP问题，TSP属于一种典型的组合优化问题，描述为在给定了n个点，要求从任一个位置出发，经历所有的点，最后回到出发的位置，且所经历的路径最短。定义两点i和j之间的距离为dij，非对称TSP问题即使dij≠dji，优化目标为路径S=dij+djk+…+dmn。一批生产任务中的取送作业是由多次复合作业和单一作业组成，每一次复合作业都可看成一个小的非对称TSP问题，通过对复合作业的组合排列达到仓库路径优化的目的。模型以优化最小化时间为主，优化的是堆垛机的空载时间。

目前市场上最常见的是货叉式单立柱堆垛机，适用于存取托盘型货物，堆垛机在巷道中的一次穿梭只能完成一个货物的存或取[6]。为了方便后续计算，结合堆垛机及仓库的实际情况作如下假设：

（1）根据作业任务指派需要访问的出入库后，堆垛机拣选出入库的时间不会随着存取路径顺序的不同而不同，其访问出入库的时间是固定的。

（2）由于存取货物时，货叉伸缩时间为恒定，假设忽略该时间。

（3）堆垛机在水平方向和垂直方向上均以恒定速度独立运行，忽略其启动及制动时间。

假设有m个入库任务，n个出库任务，且m≠n，则有min（ m,n）个复合作业需要执行。设出入库位于a列b层，货架的长度和高度分别为l和h，堆垛机起始点坐标为 （0,0 ），入库任务出入库为 （xa,xb），出库任务出入库为 （ya,yb），执行一次复合作业需要的时间为：

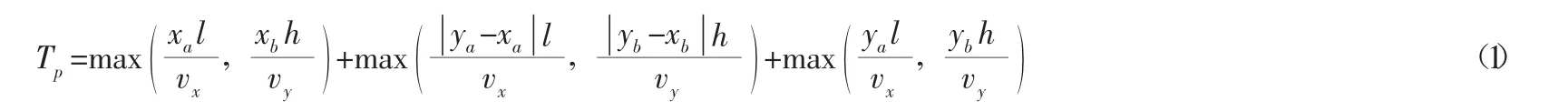
其中：p为第p次复合作业，vx为堆垛机水平运行的平均速度，vy为堆垛机垂直运行的平均速度。

其中：q为第q次单一作业。

则有仓库路径优化目标函数为：

2 ADP简介

Bellman于1957年提出了最优性原理：无论过去的状态和决策如何，相对于当前的状态而言，余下的决策序列必然构成最优子策略。Bellman把这一过程描述为如下递归等式[4,7]：

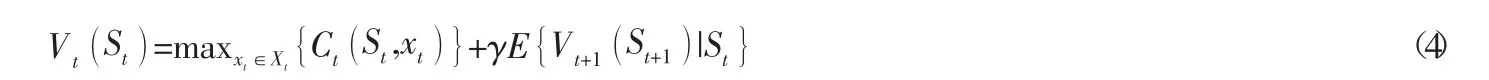
式中：Vt（St）表示当前状态St的值函数；Vt+1（St+1）|St表示下一个状态St+1的条件值函数，反映了决策xt对状态St+1及后续状态Sk值函数的影响；γ为折扣因子，体现后续状态对当前价值影响的折扣。

上式中含有期望值的计算，而现在大多问题的状态空间和决策空间是高维的，因此求出精确最优解会变得非常困难，这也是经典动态规划的缺陷之处。经典动态规划在求解问题时，需要枚举每一次迁移中的当前状态、所采取的动作、外部的随机信息和下一状态，以获得最优决策。这种方式能够获得精确的最优解，但是容易产生“维数灾难”，在大规模问题应用中受到了限制。在问题规模比较大的时候，使用贝尔曼方程递推各状态的精确值函数是不能现实的，由此产生了近似动态规划法，使用近似值函数来替代精确值函数同时减少期望的求解。

近似动态规划法的思想就是在求解问题时使用近似方法对状态的值函数进行近似，以值迭代或策略迭代的方式，不断更新状态值函数的近似估计，在迭代终止时获得问题的近似解，从而避开求精确最优解。每次迭代各时段只有少量状态而非所有可行状态参与近似值函数的计算，计算量不再随计算规模的增加指数增长，从而克服“维数灾”问题。和DP相反的是，它采取从前往后递推的方式，以避免维数的急剧增长。

ADP算法寻找最优策略路径的算法通常有两种：值迭代和策略迭代。

（1）值迭代算法通过反复迭代值函数来寻找最优值函数，即最大回报值，它是关于状态和控制动作的概率的函数，然后使用最优值函数逆向计算出一个最优策略。

（2）策略迭代算法是反复迭代策略以改进策略，在每轮迭代中，找出当前策略的值函数，而非最优值函数，然后利用该值函数计算出新的改进的策略。

本文采用值迭代算法来解决自动化立体仓库出入库路径优化问题。

3 问题求解

3.1 求解思路

应用ADP求解仓库问题的总体思路可表述为：（1）应用DP的概念和符号描述仓库路径优化问题，建立决策模型。（2）构造近似值函数并得到其线性表达式，求解由阶段状态和近似值函数构成的优化决策模型。（3）由最终的优化决策序列获取堆垛机行驶路径方案。

首先对此问题模型中涉及的时间进行说明，文中时间区间为“阶段”，时间点为“时刻”，在t时刻的系统状态为St，并在此时做出决策xt。在阶段t的时间段内，事件发生顺序如下：

（1）服务完当前的出入库，系统处于状态St。

（2） 根据当前状态做出决策xt。

（3）到达下一个出入库进行服务，计算成本Ct。

（4）服务完当前的出入库任务后，进入下一个状态St+1。

3.2 模型建立

结合ADP建立问题的优化模型，时间、状态、策略、状态转移函数，回报值函数和近似值函数等。

（1）状态变量描述系统在当前环境所处的状态，表示决策者做出决策之前的状态向量，状态变量St：

其中：t=0,1,…,n。

it：阶段t时当前服务的出入库。

jt：出入库t的状态，如果出入库i访问过了，则jt=1；如果没有被访问过，jt=0。

（2） 决策变量xt

it+1：阶段t+1要服务的出入库任务。

rt：在服务下一个出入库前，是否要返回堆垛机起始点，如果返回则rt=1，否则rt=0。

（3） 成本函数

每阶段的成本用堆垛机行驶消耗的能量表示，可以由现阶段的状态和决策来决定，表示为：

（4） 状态转移函数

状态转移函数表示为：

（5） 目标函数

目标函数是最小化所有阶段的费用之和:

将决策的目标函数式（9）转化为Bellman方程式，应用值函数近似策略求解：

3.3 近似值函数

出入库路径优化问题采用值迭代和平滑策略来获取近似值函数，具体算法步骤如下：

（1） 初始化

②设置n=1，N=50，n为取样路径标记，N为总的取样次数。

（5） n+1，如果n≤N，跳转至步骤（2）。

接下来计算近似价值函数的线性表达式，在出入库路径优化问题中，定义近似值函数是关于距离lt的线性函数。在状态S下，构造近似价值函数的线性表达式：

式中：θ1,θ2为待定参数，根据上述ADP求解问题的算法步骤（6） 达到稳态的一组有效值，采用线性回归的方法求解得到待定参数，从而得到近似价值函数的线性表达式。

得到近似价值函数后，对仓库出入库路径优化问题进行具体的指导应用，求解决策函数式（10）。

4 算例仿真

现通过一个具体实例来验证算法的有效性，假设有一个10列9层的立体化仓库，有一批出入库任务，其中有10个入库任务，8个出库任务，任务如表1所示。

表1 随机任务序列

设定模型中相应的参考数值，取l=1.5m，h=2m，vx=vy=3m/s。使用matlab进行线性拟合及编程，同时为了证明ADP具有更好地求解出入库路径优化问题的能力，对此问题分别采用ADP及DP方法进行优化。

取第50次迭代的最后一组系统状态近似值进行拟合求解，求得近似价值函数的线性表达式，如表2所示。

表2 第50次取样的系统近似值

得到近似值函数表达式如下：

利用得到的近似值函数来指导求解决策函数，得到近似最优解90.6s，具体路径如图2所示，可以很明显看出在进行优化后堆垛机行驶路径清晰明确，减少了不必要的损耗。

同样，利用DP求解同一问题得到最优解88.2s，但求解时间几乎是ADP的3倍之多，比较来看，ADP算法有效地克服了动态规划计算量大、计算时间长的弱点，提高了自动化立体仓库出入库的效率，具有明显的优越性。

5 总 结

本文针对自动化立体仓库出入库路径优化问题进行了详细研究，结合DP方法建立了考虑堆垛机运行时间最短的数学模型。在此模型的基础上，使用近似动态规划法求解该模型。与动态规划的对比试验结果表明，ADP相较于DP，减少了模型求解的计算量，缩短了计算时间，在一定程度上得到了近似最优解，很好地解决了自动化立体仓库出入库路径优化问题。不足之处在于近似值函数线性拟合存在的误差较大，以后可考虑使用可能多的离散值，或者用非线性的表达方式来得出近似值函数。

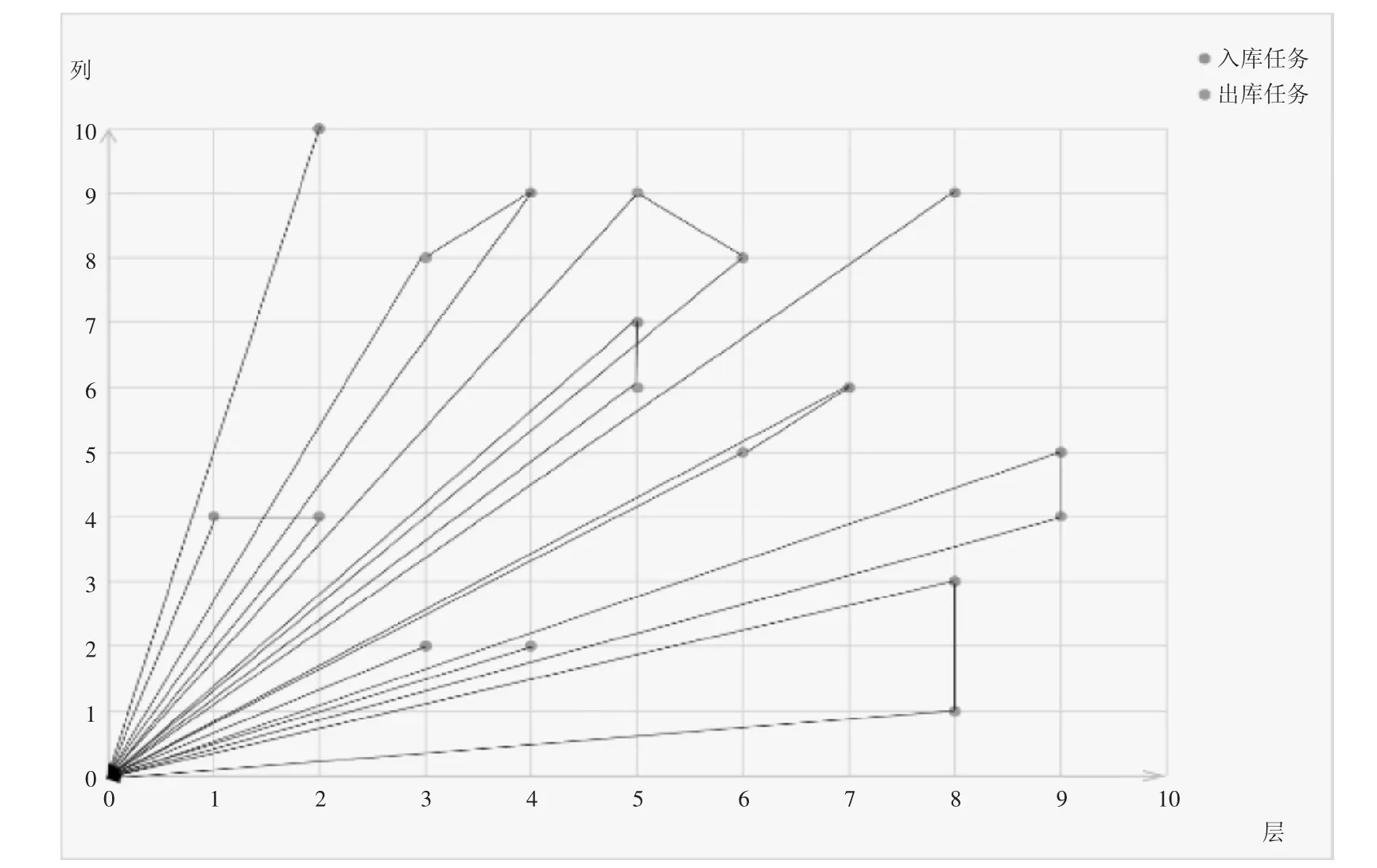
图2 优化后堆垛机行驶路径图