计量测试中异常数据的处理方式

2019-04-26林俊

电子技术与软件工程 2019年4期

文/林俊

1 计量测试中异常数据的成因分析

计量测试是一项专业性较强的工作，此项工作最为基本的要求是确保数据的精确性，为了实现这一目标，操作人员应当具有丰富的经验，并且采用的仪器设备必须具有较高的精密性。然而，受到一些因素的影响，使得计量测试中常常会出现异常数据，从而导致计量结果的准确性降低，造成异常数据的原因有以下几个方面：

（1）操作人员缺乏工作经验，在测试的过程中会出现各种失误，这样会造成检测结果的准确性不足，异常数据也会随之出现；

（2）测试仪器受到外界因素的干扰，如机械振动等，或是选用的仪器本身存在缺陷，由此会增大异常数据出现的可能性；

（3）计量测试的过程中，仪器受到电磁干扰，或是由于供电电压不稳定，使仪器发生故障，进而引起数据异常；

（4）仪器在长时间使用后，未进行及时校验，部分元器件损坏、零部件松脱，致使测试过程受到影响，导致检测结果不准确；

（5）在计量测试的过程中，通常会针对可能出现的异常数据选择相应的剔除方法，若是方法选择的不恰当，则无法对异常数据进行有效剔除。

2 计量测试异常数据的处理方式

2.1 异常数据的判断方法

在计量测试过程中，对异常数据进行判断时，应当选择正确的方法。目前，较为常用的判断方法有以下几种：

2.1.1 拉依达判断法

这种方法基于的是拉依达准则，具体的判定原理如下：假定某一组测试数据当中只包含随机误差，通过计算处理可以获得标准偏差，根据特定的概率可确定出一个区间范围，如果误差超出这个区间范围，则可将之判定为粗大误差，含有粗大误差的数据则为异常数据，需要进行剔除。该方法可对正态或是接近正态分布的数据进行有效处理，应用时，需要确保测试次数充分，若是测试次数不足，则会造成粗大误差的可靠性降低。所以当测试次数较少时，不宜采用该方法对异常数据进行判断。该方法具体的判断过程如下：

对被测试量进行等精度测量，由此可获得x1, x2, …xn，随后求取算术平均值x和剩余误差vi，其中vi可用下式表示：

上式中i=(1, 2, …n)，在根据贝赛尔公式可以计算出标准偏差σ。如果某个测量值xb的剩余误差vb(1≤b≤n)，并满足下式：

则可认为xb是含有粗大误差值的坏值，应当予以剔除。

2.1.2 格拉布斯判断法

这种方法是以测试量的正态分布作为判断前提，从理论的角度上讲，该方法较为严谨，操作过程也比较简便。该方法的判定原理如下：当某个测量值的残余误差的绝对值|vi|>Gg时，则可判定该值当中存在相对较大的误差，应当对误差进行剔除。该方法对异常数据的判断过程如下：

按照测量结果偏离真值的程度（误差理论），想要对偶然误差进行有效剔除，至少需要进行10次以上的测量，为了确保测量精度和响应速度，可将15次确定为一个单位，当获得15次测量数据后，其中可能会含有较大的误差，可以通过分检的方法，将可疑值剔除掉。当测量值xi对应的残差vi满足下式时应当该数据舍去：

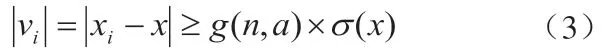
在上式当中，x表示n次采集到的平均值(∑xi)/n；σ(x)表示测量数据组的标准差，可由贝赛尔公式求取；中的n表示测量次数，表示显著性水平（可取0.01或0.05）。当测量次数n=15，显著性水平时，则随后可将15次的采集值存入到同一个数组当中，求取平均值，对残差进行计算，进而求出σ(x)，并将残差的绝对值与2.41倍的σ(x)进行比较，剔除可疑值后再次求取平均值，然后重复上述步骤验证是否仍有可疑值。在实际应用中发现，基本不需要重复，通常第一遍即可达到要求。

2.1.3 t-检验法

这是一种假设检验的方法，可在测量次数n<30的条件下使用，通过对随机变量的数学期望进行检验，看是否与某个已知的值相等。该方法的检验过程如下：

假设(x1, x2, …xn)为正态随机变量x的样本，期望Mx与已知值m0相等。按照统计理论，如果上述假设成立，则统计量服从自由度n-1的t-分布。当正态随机变量小于样本时，可用该方法对数学期望进行检验，看是否存在较为显著的差异，若是有则可将之剔除。

2.2 异常数据的处理实例

在计量测试中，对异常数据进行处理时，异常值的判断是关键环节，下面根据上述的判断方法，结合实例，分析异常数据的处理。例如，通过计量测试获得如下一组数据：10.002、10.204、10.218、10.228、10.230、10.312、10.320、10.342、10.346。按照上文中的判断方法，对该组数据中的异常值进行剔除，将置信概念的取值设定为95%，则显著性水平在该组数据中，怀疑最大的10.346为异常值，将整组数据相加之后，求出平均值为10.2317，与之相对应的x1的平均值为10.2331，δ=0.0912，s=0.0888。通过综合计算之后，得出10.346为异常值，应当从该组数据中予以剔除。应用上文中的三种判断方法对该组数据进行判定，10.346均为异常值。格拉布斯判断法中的与10.002-10.2317非常接近，由此说明该方法在三种方法中的效果最佳。计量测试异常数据的处理思路如下：先做一个统计量，当这个统计量处于规定范围内时，可认为其服从正态分布，否则可判定相关数据不服从正态分布，即其中包含异常数据，需要进行剔除。