基于二维单点频柱面成像算法的相位失配问题研究

2019-04-26叶阳阳袁明辉

光学仪器 2019年1期

叶阳阳，袁明辉

（上海理工大学光电信息与计算机工程学院，上海 200093）

引言

在安检扫描成像系统中，最常见的是采用平面扫描方式对目标进行成像[1-4]。这种扫描方式结构简单，但是无法对目标进行快速、全方位的扫描[5]。因此，研究人员提出一种柱面扫描方式。这种方式不仅能够对目标进行快速、全方位扫描，而且不存在俯仰角，不会造成目标变形[6-9]。

传统的柱面成像系统采用宽频信号对目标进行三维成像。成像系统中发射信号的功率一般较小，无法穿透目标，所以仅能够对目标表面进行检测。因此，可以利用单频信号替代宽频信号进行二维方位成像。这种方式能够在保证目标特征信息完整的同时降低数据采集量和系统成本，但是，由于单频信号距离聚焦深度有限，无法对目标的所有散射点进行准确相位补偿，从而导致部分散射点出现散焦现象。

为了解决受限聚焦深度的相位失配问题，研究人员提出了一种基于信号层的加权均值算法。这种算法通过对点扩散函数进行评价，设定散射点失焦程度标准，并以此计算出每个补偿平面的权值，最后通过累加平均的方式获得较好的聚焦结果[10-11]。

本文将这种由有限聚焦深度引起的相位失配问题变为多焦图像聚焦问题，并提出一种基于图像融合的聚焦增强方案。首先，获取不同补偿柱面所对应的补偿结果，对补偿结果进行初步筛选，去除失焦严重的图像，这样能够有效提高融合效率，降低失焦图像对最终结果的影响。然后，利用相应融合规则对多幅图像进行融合处理，得到聚焦图像。本文采用多种图像融合方式进行处理，并从图像熵、均方误差以及峰值信噪比方面比较融合性能。

1 成像原理

1.1 柱面成像系统概述

二维单频柱面成像系统结构如图1所示，其中O点表示成像场景中心，观测平面中心到场景中心的距离为R。收发机瞬时位置ra= (Rcos θ,Rsin θ, h)，其中θ表示收发机的方向角，h表示收发机的高度维位置。Lz表示观测平面的高度

维总长度。第 n (n=1,2,···,N)个目标散射点的位置 Tn=(rncosφn,rnsinφn,zn) 表示目标散射点距离场景中心的距离，其中φn表示目标散射点的方向角，为参考目标平面与场景中心的距离，Zn表示目标散射点的高度维位置。

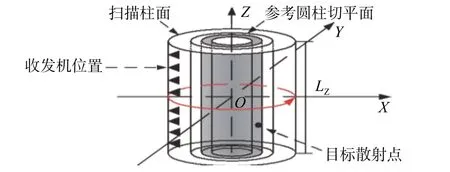
图1 柱面成像场景图Fig. 1 Cylindrical imaging scene

1.2 回波信号构建

在二维单频柱面成像场景中，第n个目标点与收发机之间的距离为：

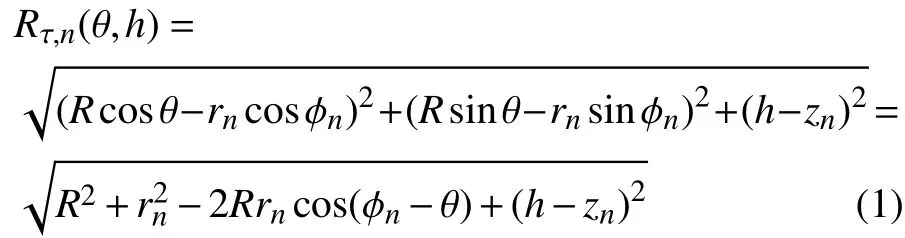
此时，由于 Rτ,n中含有余弦项 cos(φn−θ)，这将给后续计算带来难度。为了降低计算复杂度，将cos(φn−θ)利用泰勒级数展开式进行近似处理，得到

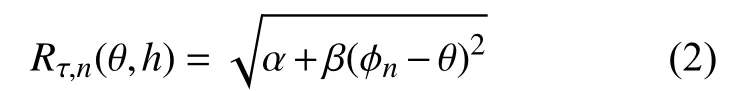
式中： α =(R−rn)2+(zn−h)2； β =Rrn。

然后，将近似结果代入原始回波信号可以得

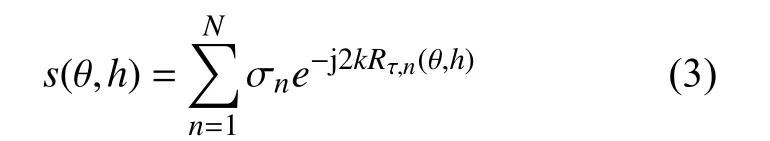
1.3 目标散射点重构

根据式(3)的回波信号表达式，将回波信号转换到波数域进行处理，得到波数域信号为

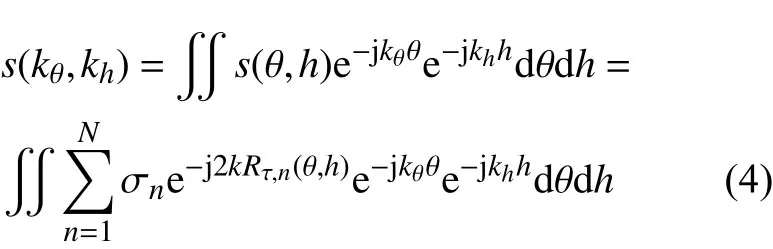
式中：kθ，kh分别表示角度维波数域频率和高度维波数域频率。

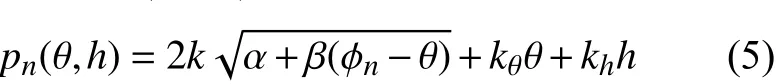
本文在目标重构中采用常见的傅里叶算法。由于利用傅里叶算法进行目标重构需要保证目标平面网格均匀，因此需要将指数项变为关于目标平面网格的线性表达式。我们采用驻定相位法分别求出 pn(θ,h)关于θ和h的驻点θ*和h*，利用驻点替代原有数据。将驻点代入式(5)并化简之后得

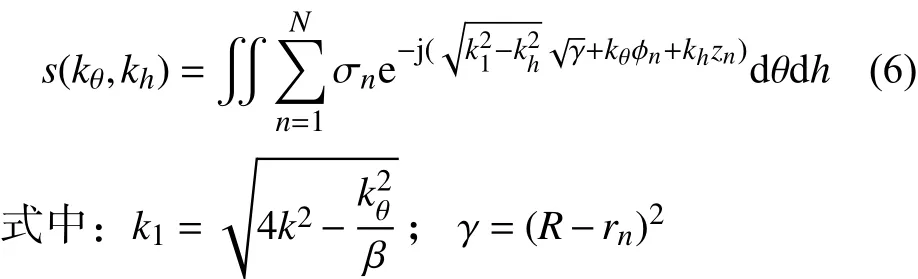
从式(6)可以看出，波数域信号指数项中包含三项，后两项可以利用对目标角度维以及高度维进行傅里叶逆变换消除。第一项针对所有目标散射点都处于同一距离维平面上的体目标而言可以看做是一个常数，但是在实际成像场景中体目标的散射点一般分布在多个距离维平面上，如果采用固定补偿项对第一项进行补偿处理，则会导致部分目标点失焦现象的发生。因此，我们采用半径为的M个圆柱切面对波数域信号进行相位补偿，其中r表示参考切平面的半径，Δrmax表示目标距离维最大偏移量。则利用第m个柱面进行相位补偿的结果为

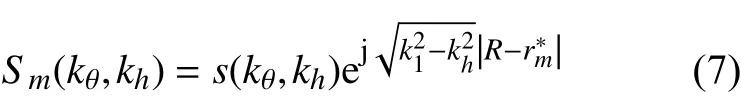
然后通过对目标平面进行二维傅里叶逆变换处理得到反演结果。

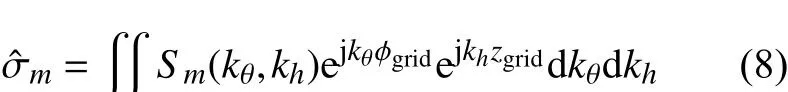
式中：φgrid，zgrid表示目标平面网格；表示利用第m个圆柱切面获得的成像结果。

首先通过比较不同距离维平面上离散目标点的成像结果，验证单频二维柱面成像中聚焦深度有限对成像结果的影响如图2所示。

从离散点的成像结果中可以看出距离维不同的散射点在不同相位补偿下展现出不同的聚焦程度。散射点的失焦程度直接影响成像分辨率。由于离散点之间存在着间隔，失焦散射点相互影响较小，因此对不同距离维连续目标进行重构，得到结果如图3所示。

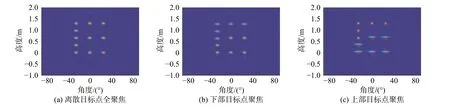
图2 离散目标点采用多个圆柱切面补偿之后点成像结果图Fig. 2 Discrete target points using multiple cylindrical sections after compensation point imaging results

图3 连续目标采用多个圆柱切面补偿的成像结果图Fig. 3 Continuous target uses multiple cylindrical sections compensated imaging results

从结果中可以看出连续目标受聚焦深度引起的相位失配问题影响严重。当目标聚焦时，边缘轮廓明显而且能量更强；当目标失焦时，边缘轮廓模糊，无法从中提取边缘特征信息，这给目标定位、目标识别等后续处理带来巨大的困难。因此，需要在不改变目标本身形状的前提下，去除失焦散射点。在文中我们将信号层的体目标在有限聚焦深度下成像问题转变为图像层多焦图像聚焦问题，并采用图像融合的方式进行聚焦处理。

1.4 图像融合处理

图像融合处理的详细流程如图4所示。首先得到经过不同半径柱面补偿结果图，其中Sm(kθ,kh)表示使用第m个相位项补偿之后的波数域回波。表示利用第m个圆柱切面获得的成像结果。

我们利用M个补偿项，构建M幅原始图像。由于这M幅原始图像中存在明显散焦的图像，因此我们需要对其进行预处理。首先，我们提取M幅图像的最大图像熵，并按熵升序排列。其次，设定阈值，去除失焦严重图像。最后，将满足阈值的图像作为原始图像，选取两幅原始图像进行融合算法处理，产生融合图像，将得到的融合图像与第三幅图像进行融合，重复此过程，直到所选取的图像被遍历并且得到最终融合结果。通过这种方式能够充分利用不同距离维信息来有效处理多焦问题，并提高最终融合图像的图像性能。

2 结果分析

图像融合技术主要应用于图像层，通过对多幅图像融合从而提高结果图像的清晰度及信息包含量，有利于更为准确、可靠、全面地获取目标或场景的信息。在本章节中将对获取的M幅图像进行多种方式的融合，并对融合结果图像进行评价与分析。融合结果如图5所示。

图5 多种图像融合方式结果图Fig. 5 Results by using multiple image fusion methods

为了定量分析比较各种图像融合算法的融合效果，本文选取了图像熵E，均方根误差RMSE以及峰值信噪比PSNR作为衡量标准，最终图像融合性能结果如表1所示。

表1 图像融合性能指标Tab. 1 Image fusion performance index

其中DWT表示小波变换图像融合算法；SIDWT表示平移不变小波变换图像融合算法；PCA表示主成分分析图像融合算法；GP表示梯度金字塔图像融合算法；LP表示拉普拉斯金字塔图像融合算法；RP表示比率金字塔图像融合算法。计算得到原始图像的图像熵为1.2073，融合处理得到的最终图像的图像熵远大于原始图像的图像熵，说明每一种图像融合算法都有效地解决由于相位失配造成的失焦问题。通过对上述三项性能指标的分析，得到基于梯度金字塔的图像融合算法能够达到更好的效果，这仅仅表示相比于其他融合算法，梯度金字塔算法更适合此场景。之后选取具体实验场景对融合算法效果进行比较。实验目标图如图6所示，采用不同的截面进行相位补偿，两个极端成像结果图如图7所示。