特征因子算法与SJR算法的比较分析及实证研究

庄纪林 庄纪林

摘要给出一定条件，实现了SJR算法向特征因子算法的转化。选取CSSCI收录的图书情报学期刊2007年互引矩阵，分别计算被引量、EF、SJR、IF、AI、SJRQ，并分成两类进行相关度分析。结果表明，在一定条件下，SJR算法可转化成特征因子算法，并且期刊评价指标EF与SJR指标显著相关，它们完全可以作为被引频次与IF的参考、补充甚至替代。

关键词特征因子文章影响分值SJRSJRQ影响因子期刊评价引文分析

分类号G35

1引言

期刊评价是文献计量学的重要应用领域，主要用于反映学术期刊的质量和水平。期刊评价的理论和方法经过长期的研究与发展，已经取得了众多成果，在实际应用方面也取得了长足进展。文献计量指标从传统的载文量、被引量、影响因子（Impact Factor，以下简称IF）[1，2]、到后来提出的h指数[3]、g指数[4]、A指数、r指数等类h指数[5，6]。随着谷歌的页面排名（PageRank）算法出世，2008年Scopus推出了基于自身数据库的评价指标SCIMAGO 期刊排名（SCImago journal rank，以下简称SJR）[7]与每篇论文的参考源标准影响引子（Source Normalized Impact per Paper，以下简称SNIP）[8]。作为回应，汤姆森路透科技集团也推出了期刊评价指标特征因子（Eigenfactor，EF）[9]作为JCR的增强功能，并于2009年初正式采用。2012年SJR和SNIP对各自的算法进行修正与改进，发表了修正指标SJR2[10]与SNIP2[11] 。2015年汤姆森路透科技集团也发布了两个新的文献计量学指标，一个是标准特征因子（Normalized Eigenfactor，以下简称NEI）[12]，一个是期刊影响因子百分位（Journal Impact Factor Percentile，以下简称JIFP）[13] 。而作为新型期刊评价指标的代表SJR和EF，两者都采用了类PageRank算法模型来评价科技期刊的质量与影响力，是当前期刊评价指标的研究热点。

几十年来，IF得到了广泛的认可和应用，然而近年来学者们把更多注意力投入到SJR和EF等类PageRank算法中，究其原因，是因为IF存在着以下几点问题[14]：

1）IF在计算过程中并没有考虑引用质量，只有对引文数量的统计。一篇学术权威发表的文章中引用的参考文献显然应该具有更高的价值。

2）在计算过程中未能排除期刊的自引行为，这使得期刊可以通过增加自引来提高影响因子。

3）IF计算方法采用的时间段为两年，由于研究领域差异性导致不同领域的论文的被引频次有较大差异。那些科研周期较长、发表周期也相对较长的领域，有可能出现引用行为因超出两年的时限不能被计入被引量，进而影响IF的计算结果。

4）SCI收录的不同学科的期刊数目差别很大，这种差别不仅反映在论文数量上，而且反映在引文数量上。而相同或相近研究领域的论文倾向于相互引证，这又反过来加大了不同学科间刊物的影响因子的差异。

5）基于少量期刊刊载大量有重大意义和影响的科研成果的研究结果，SCIE收录期刊只占全世界期刊总量的3.6%，而且语种大多为英文，非常有利于以英语为母语的国家的刊物获得高影响因子。

自从SJR和EF算法问世以来，由于这类算法不仅考虑了引文的数量，而且考虑了引文的质量，能够很容易地去除自引，其统计年限窗口也分别扩大为3年和5年，因此受到了广大学者的逐步关注与认可，国内也有很多学者对其进行了研究。《特征因子原理及实证研究》[15]一文以18种CSSCI收录图书情报学期刊为例，计算出它们的特征因子分值和论文影响分值，在此基础上对这两项指标同其他期刊评价指标的关系进行了探讨，得出了特征因子分值、论文影响分值和期刊综合指数、h指数、影响因子之间存在较强的皮尔逊相关性的结论;《SJR指数研究及其与影响因子的比较分析》[14]一文将SJR指数与影响因子各方面的特征进行了比较，并通过2007年的实际数据对这两项指标的实际效果进行了比对分析，总结了两者在期刊评价中的优势以及不足之处;《评价期刊影响力的三项指标比较研究》[16]一文以JCR中信息科学与图书馆学中影响因子排名前20的期刊为样本，对影响因子、5年影响因子、SJR以及特征因子的排名进行比较分析，得出SJR与其他三者之间没有发现显著相关性的结论。以上文章或者是实现了某种期刊评价算法并试图对评价结果进行分析，或者是对研究机构发布的多个期刊评价指标直接分析相关性。

3实证检验

从以上分析可以看出，EF算法与SJR算法存在着高度的相似性，而且在满足一定条件下，两者的迭代过程是完全一样的。可以预见EF算法与SJR算法在进行期刊评价时其结果具有高度的相关性。为此，笔者选取2008-2009年CSSCI收录图书情报学期刊2007年度互引矩阵[15]，并实现了EF和SJR算法，在相同统计年限窗口内分别统计被引量、IF、EF、AI、SJR、以及SJRQ指标，并分类验证指标间的相关度。从第4小节的分析可知，从指标间的对应关系上来看，被引量与EF、SJR相对应，IF与AI、SJRQ相对应，下面分别对这两组指标考察其相关性。

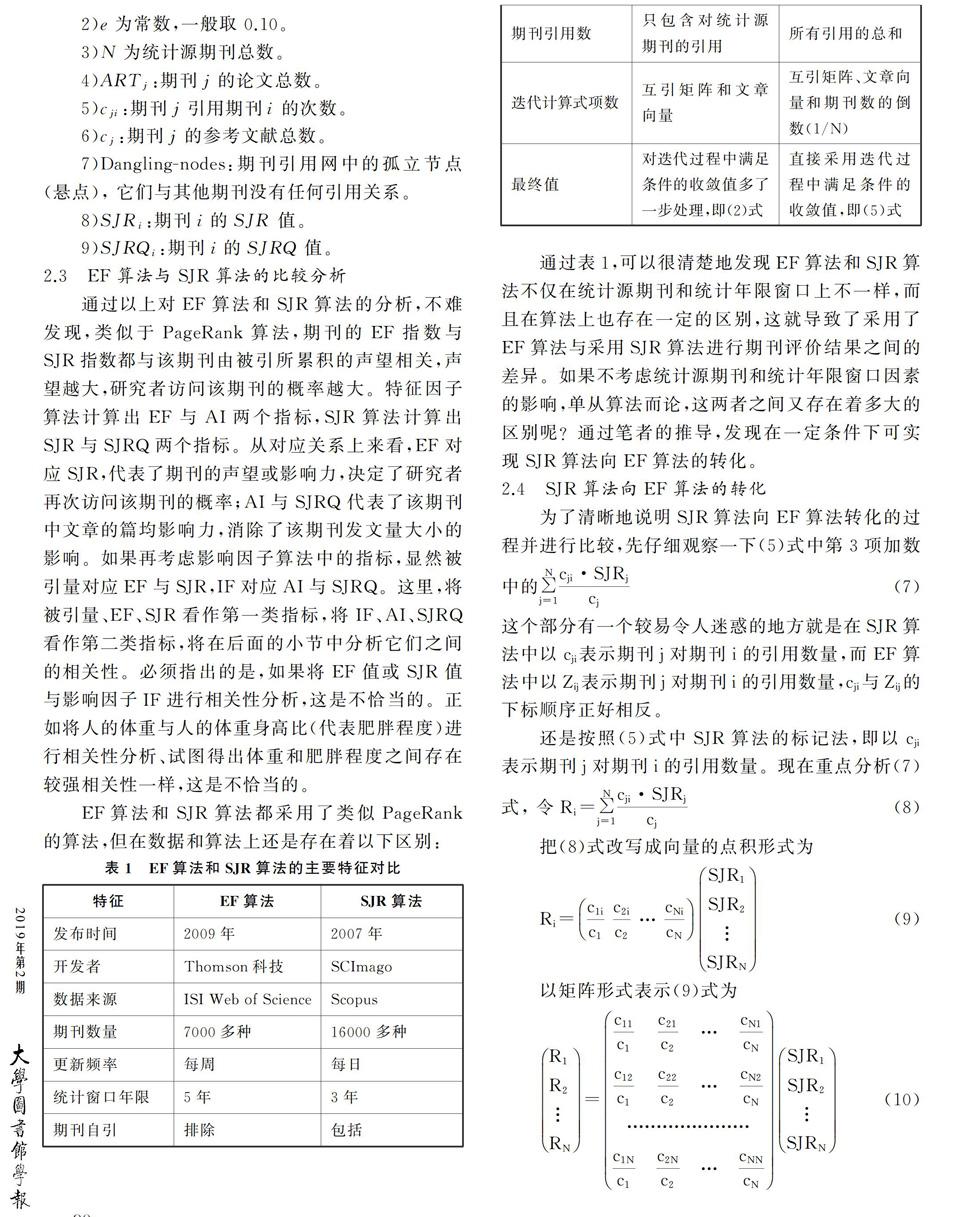
表2共包含18种期刊的互引数据，由于SJR算法中计算某期刊的引用总数时不仅包含对统计源期刊的引用数，还包含对统计源期刊外的引用数，所以这里把表2中前12种期刊作为统计源期刊，后6种期刊作为统计源外期刊。经过整理可得以下表。

需要说明的是，这里的各指标值都是在相同的统计源期刊和相同的统计年限窗口下计算的，实際上它们之间的统计源期刊和统计年限窗口不尽相同，本文统一了统计源期刊和统计年限窗口的目的是为了尽可能探索这些期刊评价指标之间的相关度。

通过表4与表5的排名来看，被引量、π*、EF及SJR之间具有极强的相关性，IF、AI及SJRQ之间也具有极强的相关性。为了进一步说明它们之间的相关性，笔者利用SPSS统计分析软件，进行相关度分析（Spearman相关系数），其结果如表6、7、8、9所示。

从表6、7、8、9可以清楚地看出被引量、π*、EF及SJR两两之间无论是数值还是排名的相关度都在0.9以上，是显著相关的;IF、AI与SJRQ两两之间无论是数值还是排名的相关度也都在0.9以上，也是显著相关的。通过相关度分析，从另一侧面说明了基于PageRank算法的EF算法与SJR算法大同小异，存在着高度的相似性。

4讨论与小结

经由前面的理论分析及算法推导，如果在计算SJR指标时：

1）调整权重令α+β=d+e=1。

2）期刊j的参考文献数只包含对统计源期刊的引用数，而不是其所有的引用数。

3）去除自引因素的影响。

那么，计算EF指标的迭代表达式（1）和计算SJR指标的迭代表达式（18）从形式和意义上是完全一样的。

同时，根据表1所列EF算法与SJR算法之间的差别，如果再满足以下两个条件：

4）统计年限窗口一样。

5）统计源期刊一样。

那么计算EF和计算SJR的迭代过程和结果是完全一样的。当然，只是“迭代”的过程和结果完全一样，并不是最终的EF和SJR值完全一样。从SJR算法的定义得SJR=π*，而EF定义成（2）式EF=100Hπ*∑i[Hπ*]i。

那么，为什么EF算法不像SJR一样直接采用π*呢？应该是出于以下几点考虑：

1）EF算法的迭代过程中用文章向量替代H′矩阵悬点列放大了悬点的作用，H是替代前的包含悬点的规范化互引矩阵，让H点乘π*可部分抵消这种替代的影响。

2）同样，（2）式分子中没有加上文章向量贡献的权重（1-α）a也是出于部分抵消迭代过程中文章向量所给予的初始值的影响。

3）（2）式中等式右边乘以100是为了换算成百分值;（2）式中分母的引入是出于规范化的目的：由于∑i[Hπ*]i=1-dπ*，d为悬点向量，所以，如果存在悬点，则∑i[Hπ*]i<1。分母的引入保证了∑iEF=100。

当然，EF算法中在得出π*后从π*到EF转换相较于SJR算法直接采用π*，这两者究竟哪个更合理，则超出了本文的讨论范围，有兴趣的研究者可以继续研究下去。

因此，虽然期刊评价指标EF和SJR之间存在着一些区别，这些区别主要表现在计算方法与来源数据两个方面：从计算方法上看，主要涉及引用关系的权重、处理自引的方式以及引用论文的统计方式;从来源数据上看，SJR指标以Scopus数据库的数据为基础，EF以Web of Science的数据为基础，SJR指标的统计窗口年限为3年，EF指标的统计窗口年限为5年。但是，由于EF和SJR都是基于PageRank算法，两者是一脉相承的，在满足一定的条件下，SJR算法的迭代式与EF算法的迭代式从形式和意义上完全一样的。

通过实证研究，发现被引量、π*、EF及SJR两两之间是显著相关的，IF、AI与SJRQ两两之间也是显著相关的。传统期刊指标被引量与影响因子虽然存在着一些缺陷，但在实践上仍存在着相当的合理性。EF算法、SJR算法作为新兴算法，克服了被引量与影响因子只考虑引文数量忽略引文质量的缺陷，也完全可以作為被引量与影响因子的参考、补充甚至替代。

参考文献

1Garfield E. Citation analysis as a tool in journal evaluation[J]. Science， 1972， 178（4060）： 471-479.

2Henk F， Moed. Citation analysis of scientific journals and journal impact measures[J]. Current Science， 2005， 98（12）： 1990-1996.

3Hirsch J E. An index to quantify an individuals scientific output[J]. Proceedings of the National Academy of Sciences of the United States of America， 2005， 102（46）： 16569-16572.

4Egghe L. How to improve the hindex[J]. Scientist， 2006， 20（3）：15-15.

5Jin B H et al. The R-and ARindices： Complementing the hindex[J]. Chinese Science Bulletin， 2007， 52（6）：855-863.

6叶鹰. H指数和类h指数的机理分析与实证研究导引[J]. 大学图书馆学报， 2007（5）： 2-5.

7Butler D. Free Journalranking Tool Enters Citation Market[J]. Nature， 2008， 451（7174）： 6.

8Henk F Moed. Measuring Contextual Citation Impact of Scientific Journals[J]. Journal of Informetrics， 2010（4）： 265-277.

9Bergstrom C T.， West J D. et al. The Eigenfactor Metrics[J]. The Journal of Neuroscience， 2008， 28（45）： 11433-11433.

10GuerreroBote V P， MoyaAnegón F. A further step forward in measuring journals scientific prestige： The SJR2 indicator[J]. Journal of Informetrics， 2012， 6（4）： 674-688.

11Ludo Waltman， Nees Jan van Eck， Thed N.van Leeuwen. et al.Some modifications to the SNIP journal impact indicator[J]. Journal of Informetrics， 2013， 7 （2）： 272-285.

12Thomson Reuters. Normalized eigenfactor score[EB/OL]. [2017-11-03] http：//ipsciencehelp.thomsonreuters.com/incitesLiveJCR/glossaryAZgroup/g9/9709TRS.html.

13Thomson Reuters. Journal impact factor percentile[EB/OL]. [2017-11-03] http：//ipsciencehelp.thomsonreuters.com/incitesLiveJCR/glossaryAZgroup/g8/9586TRS.html.

14楊康，刘明政，张旭. SJR指数研究及其与影响因子的比较分析[J]. 情报杂志，2009，28（11）：27-30.

15米佳，濮德敏. 特征因子原理及实证研究[J]. 大学图书馆学报，2009，27（6）：63-68.

16田质兵. 评价期刊影响力的三项指标比较研究[J]. 现代情报，2010，30（9）：141-143，146.

17EIGENFACTOR.org. EigenfactorTM score and article influenceTM score： detailed methods[EB/OL]. [2017-11-03] http：//www.eigenfactor.org/methods.pdf.

18SCImago Research Group. Description of scimago journal rank indicator[EB/OL]. [2017-11-03] http：//www.scimagojr.com/SCImagoJournalRank.pdf.