基于节点度中心性的无监督特征选择

闫泓任 马国帅 钱宇华

（山西大学大数据科学与产业研究院，太原，030006）

引 言

随着获取数据的手段愈加多样，包含丰富信息的高维数据涌现在各个领域，如生物信息学[1]、地理学[2]、以及社交网络等[3]。但是急剧增长的数据规模往往使得冗余信息过多、数据处理缓慢或者建模效果不佳。因此使用合理的数据挖掘技术自动提取数据中的有效信息十分必要。

低维度空间上有效的智能算法处理高维数据时常常面临维度灾难：数据变得十分稀疏，且建立在大量特征上的模型往往出现过拟合从而影响预测结果[4]。为解决这一难题，降维方法近年得到研究者的重视。这些方法大多可分为两类：一类是特征提取，将高维原始空间线性或非线性的投影到一个维度更低的特征空间[5]；另一类则是特征选择，即直接选择原有特征集中的一个子集[6]。正确使用这两类方法可以有效提高模型学习能力和泛化能力，并降低时间和空间计算复杂度。本文关注的方法以特征选择为主。

对于给定的任务和数据集，如何为模型选择合适的特征子集，这取决于在一个数据集中弃用或保留某些特征会对未来的预测结果准确性产生的影响。这种影响主要包含两方面：特征和类标签之间的相关性（简称特征关联）以及特征冗余[7]。特征关联度决定了一个特征在聚类分类等任务上有效抓取样本类别信息的能力。假如某个特征具备分辨类别的能力，则它被认为有关联；反之如果它使得原本的分辨更加模糊则被认为无关。冗余特征是一类有弱关联度且无法增加分辨能力的特征。普遍认为特征冗余是依赖于特征相关度和给定特征子集而存在的。在这些定义之下，Koller等提出了基于信息论和马尔可夫毯的特征选择理论框架和实现方法。Blum等提出逐个评估(即特征排名)方法，即设定准则对每个特征的关联度进行独立计算并排名，然后选取分数最高的一群特征作为输出[8]。此后He等[9]对样本相似性建模得到Laplacian score（详见第1节），通过构造仿射矩阵来保持数据的流形结构。

由于冗余的特征常常具有相近的分数，上面的方法无法消除冗余现象。Brown等[10]研究者的极大似然选择框架以及Liu等[11]的子集评估（搜索策略+评估停止准则）方法既可消除无关亦可减少冗余，但是搜索最小子集的策略效率不高。在此基础上Liu等[12]提出了新的选择框架，使得关联度和冗余的分析更加高效。之后陆续有新算法被提出。其中一类方法通过在已知类标签的情况下建立稀疏学习模型[13]，最小化含有稀疏正则项的目标函数的拟合误差，最后输出特征系数作为特征的排名[14]。这类方法虽然可以在优化目标函数的过程当中同时处理特征关联和特征冗余，可是它的缺陷也很明显：依赖于特定学习算法，迁移能力弱；且在正则化的限制下特征系数变得极为稀疏，从而无法充分考虑冗余特征。

传统特征选择算法会潜在假设各特征之间的独立性（此时的特征被称为flat feature），但是大量真实数据中彼此相关的特征——如健康大数据中不同疾病之间的关联或生物数据中基因之间的协调关系等，严重影响算法有效性。此后的研究文献有时在构筑模型前预先假定特征结构的存在。同样基于稀疏学习的框架，将特征当作节点，关联当作连边，文献[15]提出Lasso方法，建立特征相关性的图结构并优化特征系数。这类方法虽然提高了学习任务的效果，可求解的优化目标复杂，计算成本较高，且无法通过数据自动提取特征结构。

以上提到的方法有效地应用在标签数据上，但是对于无标签或少标签的数据，由于无法利用标签作为评价准则，效果不够理想[16]。文献[17]利用进化局部搜索算法，在无监督的情况下，能够同时找到特征组合和聚类数目，Cai等[18]提出基于稀疏学习的多聚类特征选择等经典无监督方法（详见第1节）。这些技术之所以能够产生较好的结果，是因为它们的模型把握到样本或特征的局部关联，却同时因为缺失对全局关联的考察导致选择过程无法得到宏观信息。

在无监督学习的场景下，当特征维数越来越巨大，特征空间并不明确存在分布，甚至具有很强的异质性，传统的条件概率框架或旨在利用流形学习（或稀疏学习）发掘局部信息的方法将越来越难推断什么特征更加重要。鉴于以往排名方法处理特征冗余时的不充分、特征空间的局部结构方法的局限性，本文提出启发式无监督算法框架，引入复杂网络的概念对特征的全局关联进行建模。复杂网络可以很好地模拟群体中的交互行为，群体形成的网络具有独特的拓扑性质。理解这些性质有助于认知这个群体和其中的个体。把特征空间作为一个群体，那么复杂网络能够全局地捕捉到特征之间存在的关联。在网络中，为了找到最重要的特征（节点），本文使用社会网络分析当中常用的概念——节点度中心性，衡量一个节点在网络中的邻居占网络节点总数的比例[19]来选择最重要的特征子集。在以往的子集搜索方法中，寻找到的所有子集之间存在交集，这个交集对应着空间中最重要的特征；但是真实情况下这个交集不总满足非空。相反，利用度中心性可以近似刻画这类特征：假如一个特征度中心性最大，说明它跟网络中其他所有节点之间的相关程度最小，那么它被认为无关或冗余的可能性最小，在每个不同的“最优子集”中同时出现的可能最大；相反如果一个特征度中心性最小，那么它与其他所有节点的相关程度最大，则它很有可能被判定为冗余特征。其次，在获取全局信息的基础上，对所有特征按照重要性进行排名，可以有效规避高分的冗余特征，同时不会因为简单地删除大量特征致使忽视对冗余特征的处理。

1 特征选择相关工作

过滤方法是一类重要的特征选择方法，可独立应用于数据预处理阶段[20]。其中的排名方法因其简单高效而用途广泛。它的步骤大致如下：(1)设定特征重要度评判准则；(2)根据准则给特征打分；(3)选择分数阈值并过滤掉阈值之下的特征。排名方法根据类标签的使用情况又可分为有监督排名、半监督排名、和无监督排名本文提出的方法即无监督排名方法。

无监督的排名方法将数据作为输入，通过准则为特征评分，并按要求输出高分特征，整个过程不需使用类标签信息。根据不同的特征相关准则，这些方法大致分3类。一类是基于相似度的方法[21]，通过衡量特征维持数据在流形上的结构相似性的能力判别特征重要性。首先将数据相似性编码成为仿射矩阵Α；其次选定k个特征；进而最大化这个集合在由Α诱导出的仿射矩阵B上的效用。这一类中的方法因矩阵B的设计方法改变而不同。常见方法是Laplacian score(LS)以及谱特征选择(Spectral feature selection,SPEC)[22]。在 LS中，如果 i和 j是 p-近邻，Ai,j=Bi,j=exp{-||xi-xj||22/t}，如果不是则规定 Ai,j=Bi,j=0,其中xi为样例，Ai,j为Α在(i,j)位置上的元素。在SPEC中Ai,j=exp{-||xi-xj||22/(2δ2)}(称作径向内核核函数)，B根据3个不同的打分准则分别为不同的关于Α的标准化拉普拉斯矩阵的矩阵。

基于稀疏学习和流形学习，Cai等发表多类簇属性选择(Multi-cluster feature selection,MCFS)的方法。MCFS考虑到两方面：最大程度保持数据的簇结构；被选特征的分辨能力能够对所有类簇都有效。它有3个步骤：(1)选择p近邻(类似于LS)，建立仿射矩阵S和它的拉普拉斯矩阵L，利用谱聚类技术将数据嵌入流形结构[23]；(2)使用谱回归模型对特征重要性进行度量；(3)对每一个特征打分，并选择分数最高的特征。同样，利用谱分析方法，无监督判别特征选择(Unsupervised discriminative feature selection,UDFS)[24]及非负判别特征选择(Nonnegative discriminative feature selection,NDFS)[25]着重对特征的分辨能力进行建模。

第3种是统计类方法，其中经典的Low Variance用于离散数据的无监督特征选择。给定阈值，计算特征方差。方差低于阈值的特征将被筛除。尽管这种方法可以筛选出分辨样本点能力最弱的特征，但是无法处理特征冗余现象。

此外，还有一种经典特征提取方法：主成分分析（Principal component analysis,PCA）。根据最大化方差的原则，原数据表的协方差矩阵通过正交变换，数据的协方差矩阵被转化为一个对角矩阵，此对角阵上的元素按照数值大小降序排列。每个元素（即特征值）对应于原协方差矩阵在新的坐标系下某个维度的投影，是原特征集中元素的线性组合。

这些方法虽然在一定程度上实现了降维，但是不足之处在于它们处理特征结构的能力有限。因而本文利用复杂网络，对特征之间的关系进行探索，挖掘特征之间的关联结构。尽管复杂网络研究的往往是不规则图，且节点或者连边的数量巨大，统计物理的方法论仍然可以为认知大规模关联提供助力[26]。一些用来衡量节点重要性、网络结构稳定性等拓扑性质的统计学指标相继被提出。

2 基于节点度中心性的无监督特征选择

2.1 预备知识

本文使用相关系数（或称皮尔森系数）来量化特征间（线性）相关程度，相关关系定义如下。

定义1随机变量X1和X2的相关系数为

式中σX1和σX2分别是 X1和X2的标准差。相关系数有以下特性：(1)-1≤ρ(X1,X2)≤1；(2)ρ(X1,X2)=ρ(X2,X1)；(3)ρ有尺度不变性和平移不变性；(4)ρ对散点图的旋转敏感。在复杂网络中，节点度用来衡量节点在网络中的重要程度。

定义2节点度中心性定义为

式中ki为节点i的度值，Z为网络节点个数。某节点度中心性值越大，它在网络中的重要程度越高。

表1列出文章中使用的符号及其含义。

表1 符号及其含义Tab.1 Notations

2.2 数据集

本文在6个高维数据集上进行方法验证。这些数据集描述如下（参照http：//featureselection.asu.edu）。(a)BASEHOCK，包含1 993个样例，4 862个特征，2个类别；(b)PCMAC，包含1 943个样例，3 289个特征，2个类别；(c)RELATHE，包含1 427个样例，4 322个特征，2个类别；以上3个文本数据集出自于20 newsgroups原始数据集。(d)warpAR10P，包含 130个样例，2 400个特征，10个类别；(e)warpPIE10P，包含210个样例，2 420个特征，10个类别；以上为人脸识别数据库中的两个样本。(f)USPS，包含9 298个样例，256个特征，10个类别，为手写体数据集。表2汇集这6个数据集。

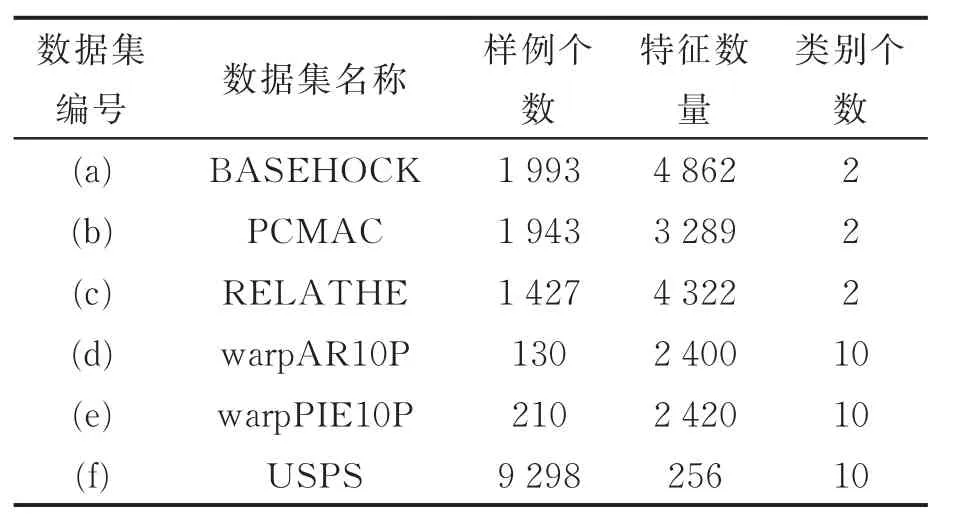
表2 数据集说明表Tab.2 Datasets

实验分析中，以下所有图示和列表中的编号(a～f)与本节数据集的编号一致。

2.3 方法步骤

本文介绍一种基于节点度中心性的无监督特征选择方法（Degree centrality based feature selection,DCFS）。先利用特征和它们的关联构建网络G(V,E)，再通过复杂网络的节点度中心性筛选符合标准的特征。基本步骤如下：

(1)算法首先计算f1,f2,…,fM两两间相关系数ρij≕ρ(fi,fj)，进而将所有的ρij组成相关系数矩阵(ρij)M×M，以此表示整个特征集之内的全局关联。

(2)对所有系数进行归一化,其目的是将所有特征间的相关成都放在同一尺度下进行比较。归一化形式为

(3)为了下一步构建特征网络并提取这一网络里的拓扑信息以便寻找有影响力的特征，需要选定筛选阈值0＜ θ＜ 1，用以过滤{ρij：ρij≥ θ}且同时保留低于阈值的关联。其合理性在于，如果把特征视作数据聚类的参照，本文启发式地认为正相关性较大的两个特征观点相近，相关性较小的两个特征往往观点无法比较，而负相关性较大的观点近乎相左。在这里更关注相关性小的或负相关性大的关联。

(4)ρ的对称性导致网络是无向的。此外本文认为每个小于阈值的关联都对整个网络产生同等的效用。令φθ是[-1,1]上的阈值函数

利用φθ将关联关系二值化，换言之原来的由相关系数组成的邻接阵矩阵变为了布尔型邻接矩阵。

(5)将上面的布尔矩阵转换成无向图，其中特征是节点，关联是连边。

(6)继而算法使用复杂网络中的指标来度量节点影响力，为了计算的便捷性，选取节点度中心性指标。计算G(V,E)中所有特征的后将它们排序。

(7)根据特征选择数量k,选择排序结果最大的k个节点指标进而得到这些指标对应的特征。

DCFS流程见图1。本算法结果强烈依赖θ的取值。θ取值不同，节点度中心性诱导出的最优特征随之改变。考虑以下情况：如果令θ=1,得到的网络是无权无向完全图，此时无法通过节点度中心性来判断特征的重要性，算法将按照构图时排列特征的顺序进行特征选择，最终导致特征选择失效；θ=0意味着完全忽略了非负相关系数的关联，那么生成的特征网络便无法全面地权衡特征重要性；从图2可以看出归一化后的相关系数的值分布形状不同，假如在(a)(b)或者(c)中令θ=0.5，得到的网络将基本呈现完全图的样貌，预期的特征筛选结果将会非常不理想。因而选取适合归一化后相关系数的值分布的θ非常重要。

图1 基于度中心性的无监督特征选择算法Fig.1 Degree centrality based unsupervised feature selection algorithm

图2 归一化相关系数分布图Fig.2 Distribution of the normalized correlation coefficients

从特征相关性来讲，DCFS在保留全局信息的同时将特征冗余转化为相关关系冗余。衡量一个特征好坏取决于它和其他所有特征之间的关系。删除关联可以一定程度上改善特征冗余：如果一个特征与其他特征之间的关联都很大，那么通过合理筛选θ值，这个特征的度中心性在构建出的网络中将会比别的特征的度中心性小。

3 实验过程和分析

本文先进行对照实验，实验结果比照4种降维算法：PCA，LS，MCFS，SPEC。所有方法选择的特征分别在K均值聚类(K-means)方法上进行验证，然后使用标准互信息（Normalized mutual information,NMI）来衡量预测标签和真实标签之间的差距。令c标识真实类标签向量，c'表示预测类标签向量，它们之间的互信息MI(c,c')定义为

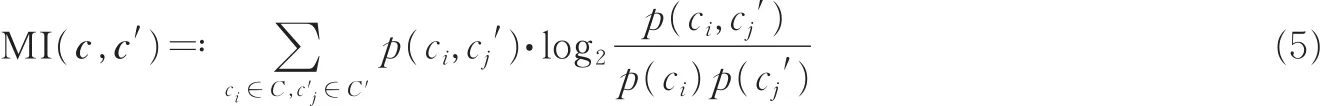
式中：p(ci,cj')是c和c'的联合概率分布函数；p(ci)和p(cj')分别是c和c'的边缘概率分布函数。NMI定义为

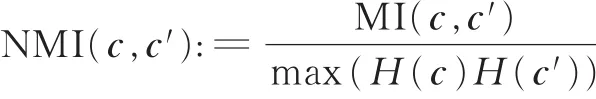
式中 H(c)和H(c')分别为 c和 c'的信息熵，NMI取值为[0,1]。

对比实验中，限定k在10～200的范围之内。DCFS仅有的一个参数θ，需根据数据集的特征相关系数的值分布（见图2）进行调整。在以下实验中，不同数据集上设定不同的θ值。图3是几种方法在6个数据上的性能示意图，其中：图3(a)为BASEHOCK上的对比结果，θ=0.4；图3(b)为PCMAC上的对比结果，θ=0.2；图3(c)为RELATHE上的对比结果，θ=0.15；图3(d)为warpPIE10P上的对比结果，θ=0.6；图3(e)为warpAR10P上的对比结果，θ=0.05；图3(f)为USPS上的对比结果，θ=0.5。

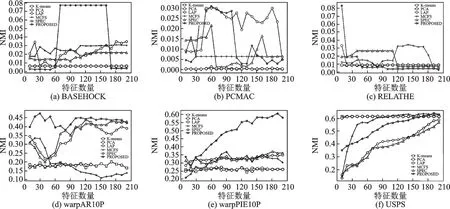
图3 对比实验结果Fig.3 Compared results of proposed method and other five comparative methods

DCFS在图3(a)，(d)，(e)上表现出很大优势。(a)中特征选择数量从70变动到140的过程中，DCFS的效果保持稳定，此时可以认为特征数量为70且θ=0.4时，DCFS达到最优，之后增加的特征（排名71～140）为冗余特征，并未影响聚类算法的判别能力。当k＞140,算法判别能力急剧下降。DCFS的性能在(d)上随k值增大而增大。在图3(e)上特征数量较少时略有波动，而后趋于平稳。图3(b)和(c)显示DCFS在特征数量较少时效果较好，并在某k值达到最高峰值；但是特征数量上升时，NMI剧烈震荡并下降。图3(f)中的DCFS方法效果并不突出，考虑到USPS数据集的特征数量，由于特征数量很少（M=256），θ取值为0.5时，特征网络中的结构不够清晰，所有节点的度中心性比较接近，所以导致对K均值聚类的效果提升并不大；在θ=0.1时，特征网络只有很少的节点(34个)和连边（62个），不足以反映全局的特征结构。图4中图3(d)和(e)数据集从类型、特征数量和标签数量等方面看非常相似，结果却不太相同，可能的原因为：特征向量的维度决定关联度的准确性。实际上，此时选择结果显示，样例少的warpAR10P（N=130）的准确度低于在warpPIE10P（N=210）上的准确度。图2所示为USPS在不同阈值下的特征网络G(V,E)。表3为6种方法的性能比较。

图4 USPS在不同[θ]下构建的网络Fig.4 Feature network of USPS under different[θ]

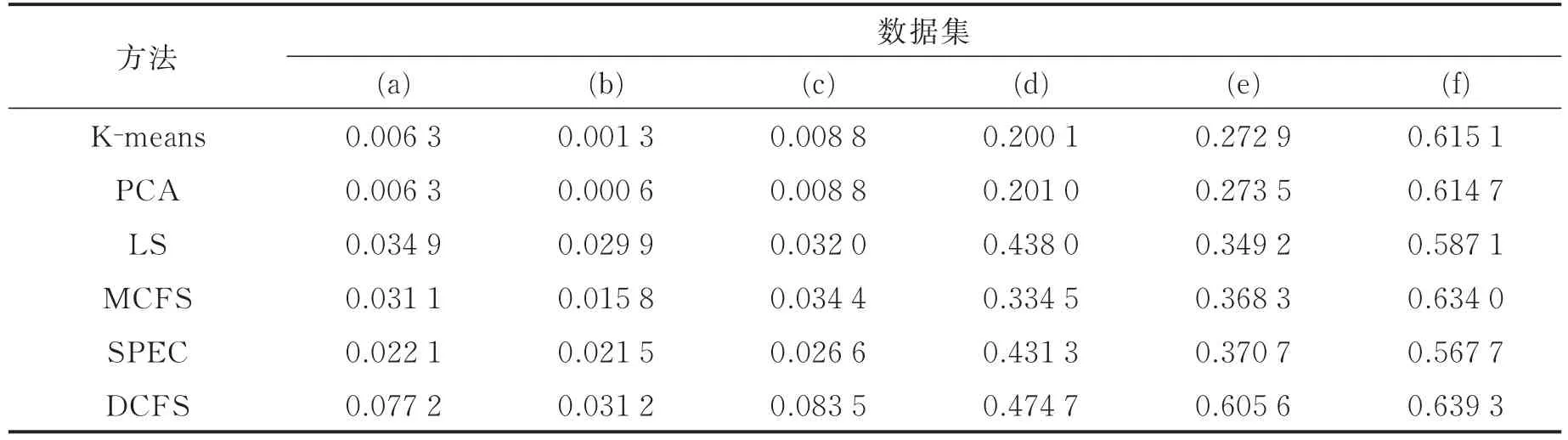
表3 各特征选择方法最佳性能对比Tab.3 NMI value comparison among six methods

从图2处观察到在3个（离散）文本数据上相关系数的分布聚集在很窄的范围；相反3个连续数据集上的分布相对平滑。其原因是在这些离散的高维数据中数据更加稀疏。对于j≠k，稀疏程度高将大概率导致xij≠xik。可以看到DCFS方法比其他方法更适合处理类似旳稀疏数据。

为了测试DCFS在数据集上的稳定性，本文接下来研究NMI关于θ和k的变化。从θ方向改变时，网络结构会发生变化，重要的节点随之变动进而影响实验精度，实验精度在某θ处浮动越剧烈表明获得的特征子集变动越大；沿k方向变化时，精度的变化表征了冗余特征数量的增减。这个实验的θ和k的取值范围维持之前对照实验设置，同时将θ的步长设为0.05，再使用网格搜索方法计算对应于所有(θ,k)的NMI值，并绘制三维直方图。图5所示为6个数据集上的三维直方图。k较小时（实验中取10～200），DCFS产生最大峰值的位置相对集中。在RELATHE集上，存在1个非常显著的极大值，说明DCFS在RELATHE上极不稳定；另外2个文本数据集上有限个局部取得显著NMI值；剩余3个连续数据集上的变化比较平缓，算法对θ和k的变化不敏感。

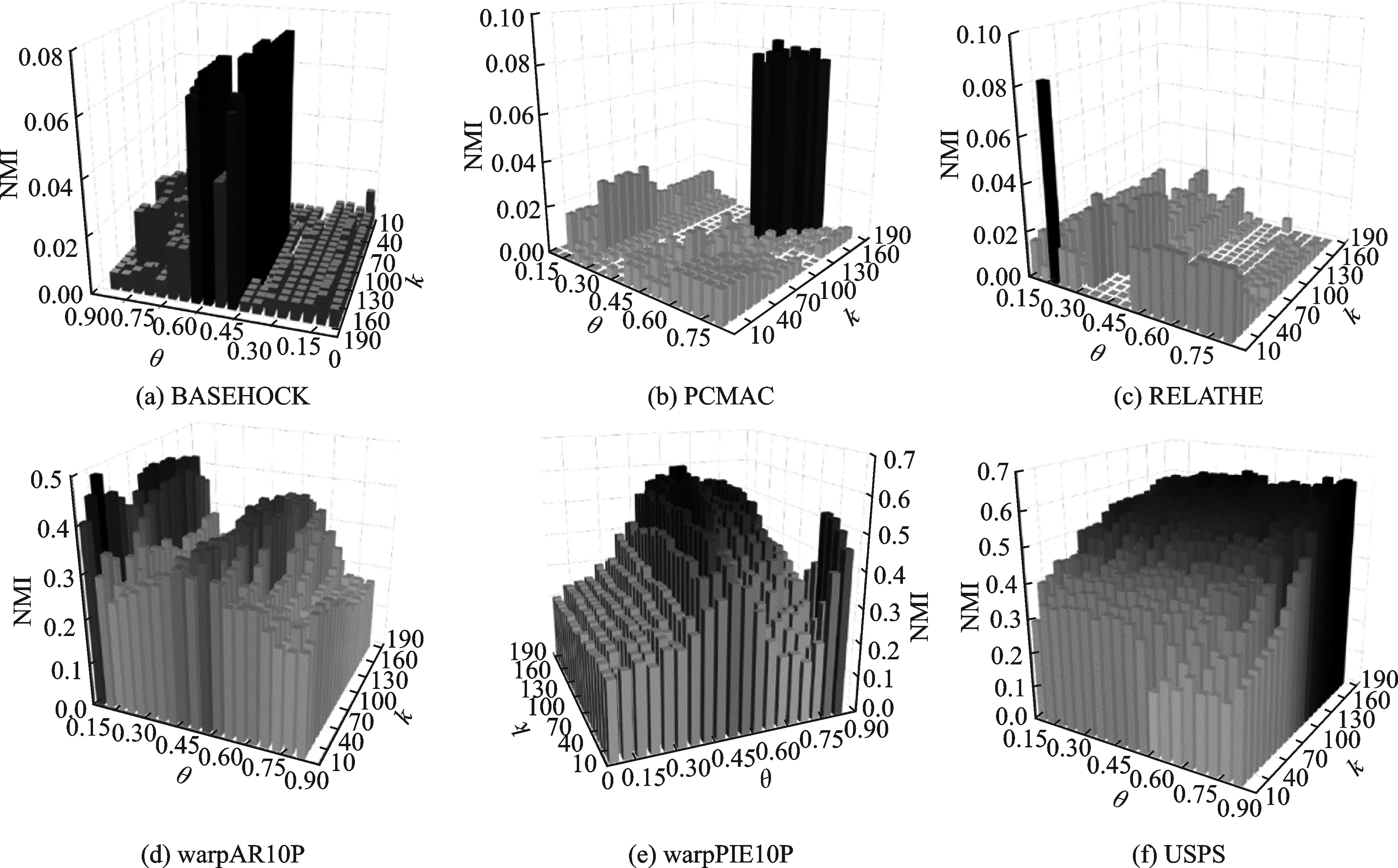
图 5 NMI-(θ,k)三维直方图Fig.5 3D histogram of NMI-(θ,k)

4 结束语

本文将复杂网络的节点度中心性引入特征选择，构建出的特征网络的结构随阈值而变化，具有灵活适应数据集中特征关联结构的能力，有助于选出同数据标签关联度最大的特征子集。另一方面，阈值θ的调节还在一定程度上缓解了特征冗余现象。实验结果表明在一些高维稀疏数据集上此方法是可行的。这种将复杂网络拓扑性质和特征选择结合的方式还有很大改进空间。本文方法利用统一θ值筛除不符合条件的关联，虽然可以处理冗余现象，但是也过滤掉一些有用特征。使用集成方法设置多样性更强的选择框架有望改进这一缺陷。其次，相关系数局限于量化变量的线性关系，从而忽略数据中的大量而复杂的非线性关联。下一阶段的研究将探索一种适用性更广的关联度量。另外，本文算法考虑到计算成本，选择了方便计算的节点度中心性来构建特征关联网络。为更好地寻找特征网络间的结构，更细致地探索特征间可能广泛存在的联系，未来也将考察其他拓扑指标的合理性。