一种基于压缩感知和动态时间规整的信号肽特征提取新算法

张洋俐君 高翠芳 陈 卫 田丰伟

（1.江南大学理学院，无锡，214122；2.江南大学食品学院，无锡，214122）

引 言

分子生物学研究已进入后基因组时代,其中心任务是更多地关注基因组表达的蛋白质结构和功能。由于基因功能最终通过其表达产物——蛋白质来实现，因此要了解基因组全部功能活动，最终也必须回到蛋白质上[1]。随着研究的深入，发现信号肽是引导新合成蛋白质实现转移的标志性序列，很多模式生物的蛋白质可通过分泌方式输出到发酵液。而且信号肽对蛋白质的定位有着非常重要的作用，使得信号肽的研究不仅具有重要的理论意义，而且也具有潜在的应用价值[1]。这使得准确地识别出信号肽成为了首要工作。

原始信号肽序列用字母符号表示，这种符号不能直接作为识别算法的计算数据。为了方便计算和进行数据处理，必须把符号序列转化成用数字表示的特征向量，因此在信号肽识别的智能算法中，特征提取起着关键作用。但是，信号肽一般由15～30个氨基酸组成，其长度变化和氨基酸序列变化都很大，而且不同种属的信号肽的长度也有所不同，这对信号肽的识别造成很大困难，而要准确地识别区分不同种属的信号肽，以达到实验或研究的目的更是一个巨大挑战。通常很难找到那些最重要的特征，或受条件限制不能对它们进行测量，这就使得信号肽的特征提取任务复杂化[2-4]。

对于信号肽的特征提取研究，已经有学者提出了数理统计方法和频谱分析方法，如氨基酸组分特征[5]，小波能量特征[6]和马尔科夫转移特征[7]。其中马尔科夫转移特征既包含了氨基酸残基的出现次数，又体现了氨基酸的排列顺序。压缩感知技术(Compressive sensing,CS)，即超完备基的稀疏线性表示问题[8-10]，是由Donoho等人在2006年提出，利用变换空间来描述信号，在保证信息不损失的情况下，把对大量稀疏信号的采样转变为对少量有用信息的采样，用测量矩阵将高维信号投影到一个低维空间上，得到具有高判别性的观测信号[11]。另外，动态时间规整算法（Dynamic time warping，DTW）[12-13]的主要思想是把待识别的时间序列与参考模板的时间序列伸长或缩短，直到它们的长度一致，然后利用欧式距离来度量两个时间序列之间的距离[14-16]。由于时间弯曲距离具有的优秀的非线性对齐特性，即使是长度不一致的序列，在计算相似度上也非常准确，使其在语音识别领域成功解决了中发音长短不一致的问题。在这一对齐过程中，两个不同长度的时间序列会进行非线性的规整，找出相互间的最佳对应点，然后计算对应点间的欧式距离，从而获得两条曲线间的相似度，非常适用于分析长度不同的信号肽序列。

在上述研究的基础上，本文先用马尔可夫转移频次矩阵将信号肽转化为稀疏信号，以形成一个数字特征矢量，再把包含氨基酸组成、排列顺序、结构等重要信息的数字特征矢量转化成稀疏向量并压缩投影，然后运用压缩感知技术提取特征对提取的特征结合动态时间规整算法，将特征向量非线性地弯曲成标准模式，最后采用支持向量机(Support vector machine，SVM)进行分类验证。以这样的方式结合DTW得到的特征向量能有效地反映出信号肽的结构特征信息，比单纯使用压缩感知技术得到的特征具有更好的分类识别准确率。本文提出的方法能简单地运用到其他生物序列的识别过程中，并且这种算法能够学习出序列中潜在的结构特征，使其在进行序列分类时具有一定优势。

1 材料与方法

1.1 采用压缩感知提取低维观测信号

压缩感知理论建立了新的信号描述和处理理论框架，能很好地应用与处理信号肽高密度的符号序列信息[11]。

设x∈RN为长度为N的一维信号，可由一组正交基（稀疏基）ψ 展开，即

式中：ψ =[ψ1,ψ2,…,ψN]为N×N矩阵，ψi(i=1,2,…,N)为N×1的向量；θ =[θ1,θ2,…,θN]为由N个稀疏系数θi=ψiTx构成的N维向量。当信号x在正交基ψ 上仅有K(K≪N)个非零系数时，则称ψ 为信号x的稀疏基。

对于信号x，可将其投影到一个测量矩阵Φ =[φ1,φ2,…,φM]上，得到信号x的M个线性测量，即可表示为

式中：Φ 表示M×N的测量矩阵，s表示长度为M的测量向量。将式(1)代入式(2)得到

不难看出，原始的N维信号x降为M维观测信号s，测量值s并非信号x本身，而是从高维降到低维的投影值。从数学角度分析，测量值是传统理论下的原始样本信号的组合函数，即测量值是包含原始样本中所有信号的少量高密度信息。

对于结构多样的信号肽S，根据上述理论，先构建出信号肽序列的马尔可夫转移频次矩阵（Markov矩阵U）。信号肽序列通常用一条有顺序的符号分布集合来描述，序列链接结构中共有20种天然氨基酸，如果把链上的氨基酸残基视为转移状态，用氨基酸残基的排列顺序反映状态间的内在关系，信号肽序列就是一个马尔可夫过程[2]。首先构建一个20×20的Markov矩阵U，矩阵中i行（代表氨基酸X）j列（代表氨基酸Y）的元素为k，表示的是X在前Y在后的相邻两个氨基酸在序列中出现的频次为k次。将U按行展开，得到一维数字序列x，长度为400。由于信号肽一般由15～30个氨基酸组成，L≪400（其中L为信号肽的长度），信息序列x已经足够稀疏，根据Markov矩阵的构建原理，矩阵本身有一个重要的特征就是稀疏性，数据中只有小部分对后续识别是有用的，需要保留，而其余的大部分则要舍弃，相对于信号长度，只有极少数的几个系数非零，其余系数均为零，非常符合稀疏信号所具有的结构特性。所以本文采用单位正交基作为稀疏基。测量矩阵选择独立同分布的高斯随机矩阵记为Φ ，计算内积可得到低维观测信号s[11]。

图1显示了将一个原始信号肽的氨基酸符号序列S使用压缩感知技术进行特征提取，得到低维观测信号s的过程[2]。

图1 提取信号肽的压缩感知特征过程示意图Fig.1 Extraction of signal peptide Feature-CS process diagram

图1 中：S为原始信号肽的氨基酸符号序列；U为20×20的马尔可夫转移频次矩阵；x为长度为400的一维数字序列；ψ 为400×400的稀疏基，本文选择单位正交基E；θ 为一维信号x在稀疏基ψ 下的展开；Φ为m×400的测量矩阵，本文选择高斯随机矩阵；s为压缩后的测量数据，长度为m，m≪400，s即为压缩感知特征；m为压缩感知特征的维度，本文取m=20。

1.2 采用动态时间规整算法提取信号肽特征向量

动态时间规整通过对输入信号进行伸长或缩短直到与标准模式的长度一致，从而克服时间序列长度的不同，提高识别率。该算法对其他时间序列如原始蛋白质序列及其特征提取序列同样适用。

动态时间规整算法能够将它们在时间维度中非线性地弯曲，然后找出两个时间序列相互间的最佳对应点，得到这两个序列之间的最佳匹配，以确定他们的相似性程度，这种序列比对方法经常用于时间序列分类。其匹配原理如图2所示。

一段用特定字母表示的信号肽可以被看成是一组时间序列，用压缩感知技术降低原信号中的冗余信息，所得到的压缩感知特征便是它直接从连续时间信号变换得到的压缩信号。接着再对压缩感知特征向量结合DTW，以期将特征向量非线性地弯曲成标准模式后能更准确地识别出信号肽中的特征结构，从而提高信号肽识别准确率。

常用的最近邻动态时间规整算法的思路是先算出测试样本与每个训练样本的动态距离D，然后将测试样本归类为与它最小动态距离的训练样本那一类。该方法思路简单但却非常有效。序列Q=[q1,q2,…,qn]与序列C=[c1,c2,…,cm]的时间弯曲距离D定义如下[17]

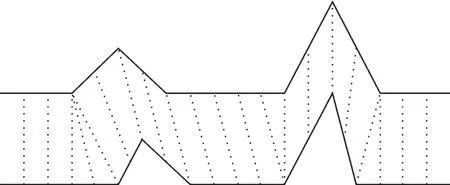
图2 动态时间规整算法的序列匹配示意图Fig.2 Schematic diagram of sequence matching based on dynamic time warping algorithm

式中：wk=(i,j)表示的是第k条路径中序列Q的第i个向量与序列C中的第j个向量是对应向量（对应点）；W为最佳路径，表示的是此路径能使式(4)的值最小。

最近邻动态时间规整使得测试集非常依赖与它动态距离最小的训练样本，而其他训练样本几乎对它没有影响。本文将采用另一种方法结合DTW，通过这种方法提取的特征能更好地结合机器学习方法，从而学习出信号肽中特征结构的位置信息，更有利于准确分类。

为了保证结果的稳定性，本文实验均采用交叉验证法。例如采用十重交叉验证法步骤如下：先将数据分成10份，取第一份作为训练集Q，其他为测试集C进行实验得到第一个准确率；再取第二份为训练集，其余为测试集进行实验得到第二个准确率，以此类推，最后对10个准确率求平均值作为最后的分类准确率。由于采用的数据都是由分泌蛋白和非分泌蛋白两个部分组成，因此在分成10份的过程中分别将分泌蛋白和非分泌蛋白各自分成10份，然后同时取它们的一份组成训练集，剩下的再组成测试集。

结合DTW算法提取新的特征来代替原来20维的压缩感知特征s。将第一个测试样本C{1}与第一个训练样本Q{1}得到的时间弯曲距离D(C{1},Q{1})作为该测试集的第一个特征，再以该测试样本C{1}与第二个训练样本Q{2}的时间弯曲距离D(C{1},Q{2})作为第二个特征，以此类推。最后，把得到的新的特征称为动态规整特征[15]。值得说明的是，新提取的特征的维度取决于训练集中训练样本的个数。为了更清晰地展示算法，以数据集Eukaryotes的特征提取过程来说明。Eukaryotes共包括1 009个分泌蛋白和269个非分泌蛋白数据。首先分别取前101个分泌蛋白和前26个非分泌蛋白（共127个数据）组成训练集Q，剩下的908个分泌蛋白和243个非分泌蛋白（共1 151个数据）组成测试集C。由于这时的训练集和测试集仍然是以压缩感知特征表示，因此分别把训练集和测试集以QCS,CCS表示为

接着结合DTW，将测试集以动态规整特征表示为

其中时间规整距离D的算法参考式(4)，同理训练样本也需要替换为

替换之后样本为

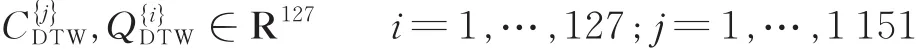
值得注意的是，所有数据集的压缩感知特征是20维的特征，是因为1.1节中取压缩维度m=20。采用十重交叉验证的Eukaryotes数据集动态规整特征是127维，但同样采用十重交叉验证的Gram+数据集，由于其训练集是由14个分泌蛋白和6个非分泌蛋白组成，它的动态规整特征也是20维。也就是说，在不同的数据集上采用上文的方法提取动态规整特征通常得到的是不同维度的特征，其维度是由入选为训练集的样本个数确定的。

另外，由于动态规整特征的每一个分量都是计算动态时间距离得到的，当数据样本很多的时候具有较长的算法运行时间。为了节约运算时间，进一步采用带限制窗的动态时间规整算法(DTW-R)，在动态时间规整的基础上添加一个限制窗，使得时间序列的弯曲程度不会过大，在一定程度上不会影响识别率，却能极大地节省运算时间。

2 实验与结果分析

实验采用的标准数据集来源于Nielsen等发布的网站http：//www.cbs.dtu.dk/ftp/signalp/[18]。选择了其中 3 个物种：(1)真核细胞(Eukaryotes)，(2)革兰氏阳性真细菌(Gram+bacteria)，(3)革兰氏阴性真细菌(Gram-bacteria)。对于分泌蛋白，数据集中给出的是信号肽的扩展序列，就是延长到包括部分成熟蛋白序列（与信号肽相邻的30个氨基酸残基）。对于非分泌蛋白，由于不存在信号肽，数据集中给出的是前70个氨基酸残基组成的序列片段。数据集信息如表1所示。

本文对Eukaryotes,Gram+bacteria,Gram-bacteria三个物种的数据集分别采用压缩感知技术、氨基酸组分[5]以及尺度小波分析法[6]提取特征。然后再对上述特征向量按1.2节的方法结合DTW，分别得到结合DTW的压缩感知特征(Feature-CS-DTW，也称为动态规整特征)、结合DTW的氨基酸组分成分特征(Feature-AAC-DTW)、结合DTW的小波能量特征(Feature-SW-DTW)。

首先，对上述特征向量使用机器学习算法验证分类准确率。本文所采用的是目前影响力较高的支持向量机LIBSVM[19]。对于LIBSVM的主要参数设置，首先使用的是以多项式为核函数，深度分别取1,2,3代表线性函数，二次函数，三次函数，这样可以防止欠拟合与过拟合，最后选取最高的分类准确率。除此之外对支持向量机未作更多的参数设置，这是为了说明特征提取方法不依赖于支持向量机的参数设置来得到更高的分类准确率。使用3种特征向量得到的分类结果如表2所示。

通过表2可以发现，结合DTW之后：对于压缩感知特征，因其是包含了序列结构信息的高密度信息特征，通过引入时间弯曲距离，对整了序列的结构信息特征，能更好地识别出信号肽，分类准确率得到提升；而氨基酸组分特征并不能体现序列的结构信息，所以准确率没有明显的变化；相反地，对于小波能量特征，结合DTW之后反而破坏了原来特征的信息，降低了分类准确率。

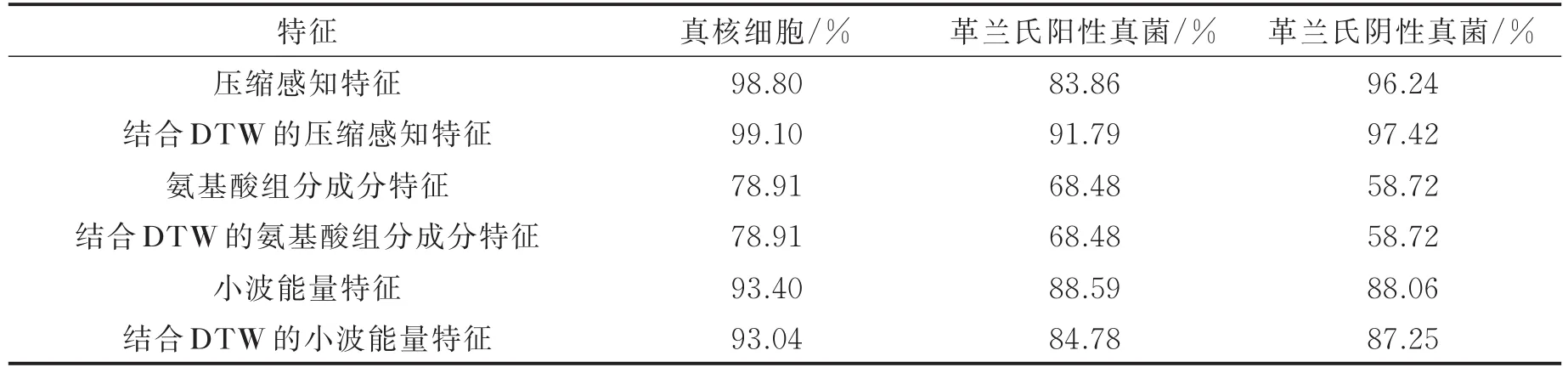
表2 结合DTW算法的前后对比Tab.2 Feature comparison before and after combining with DTW

为了充分利用数据集，同时保证结果的稳定性，本文采用的是十重交叉验证，即入选为训练集的数据样本个数是整体的1/10。现在考虑采用五重交叉验证的方法，每次入选为训练集的样本个数增加到整体的1/5（训练集样本个数的增加意味着实验次数减少），由此来分析训练集样本个数对实验结果的影响。实验表明压缩感知特征的准确率分别为98.63%，86.10%，96.40%，而动态规整特征的准确率分别为99.34%，96.71%，97.56%。

图3是对3个数据集分别采用两重、三重、五重、十重和二十重交叉验证得到的压缩感知特征与动态规整特征分类准确率的对比，纵坐标表示最后的分类准确率。

图3 压缩感知特征和动态规整特征在不同重数交叉验证算法下的分类准确率对比Fig.3 Performance comparison between Feature-CS and Feature-CS-DTW with different fold cross verification

由图3可以发现，动态规整特征得到的分类准确度始终高于压缩感知特征。所以，压缩感知特征在结合了DTW之后，具有更好的分类准确率。因此动态规整特征结合机器学习理论，通过将序列在时间维度中非线性规整，能有效判别出序列是否具有特定的结构信息，从而判别是否为信号肽。

对压缩感知特征使用不同重数的交叉验证中，得到的分类准确率有小范围的波动，仅在Gram+bacteria数据集的波动比稍大，这是由于Gram+bacteria数据集的数据较少，当采用二十重交叉验证时，入选为训练集的样本个数仅只有10个，因此在使用支持向量机分类时，由于未充分训练导致了较低的分类准确率。另外，在对动态规整特征使用不同重数的交叉验证中，发现随着交叉重数的减少（意味着训练个数的增多），分类准确率存在一定程度的增加。但是一味地增加训练个数并不一定提升分类准确率，当采用了两重交叉验证的时候，由于实验次数比较少（只有2次），单次实验的偶然性容易导致整体的分类准确率较低。此时应在使用交叉验证算法时，既要考虑训练样本不会过低，又要考虑实验次数不能太少。最后，针对数据集样本的特性，对3个数据集都采用三重交叉验证来进行数据处理。

虽然增加训练样本个数能一定程度上提高分类准确率，但是从DTW的算法原理可知，增加训练集个数同时意味着增加动态规整特征的特征个数，而动态规整特征的每一个维度是计算动态时间距离得到的，当数据样本很多的时候算法运行时间代价会较长。比如在对数据集Gram+bacteria动态规整特征进行分类运算的时候，程序一共耗时32.54 s，而在数据集Eukaryotes上，程序一共耗时1 159.13 s。这说明，数据集上的样本数据越多，使用此方法耗时便越长。为了减少计算代价，采用了带限制窗的动态时间规整方法(DTW-R)，使得时间序列的弯曲不会过大，在不影响识别率的情况下节省运行时间。

然后对数据集Eukaryotes在不同交叉验证算法下分别采用DTW和DTW-R进行特征提取，对程序运行时间进行对比，得到结果如图4所示。图中黑色表示采用DTW，白色表示采用DTW-R提取特征。可以发现在不同的交叉验证算法下，结合DTW-R程序所耗费的时间是结合DTW的1/5左右，说明DTW-R算法计算代价较小，节省时间。

接着对3个数据集分别采用DTW和DTW-R进行特征分类，并对运行时间和分类准确率进行对此，结果如图5所示。同样，图中以黑色表示采用DTW，白色表示采用DTW-R，横坐标1,2,3分别表示数据集真核细胞，革兰氏阳性真菌，革兰氏阴性真菌。从图5中发现DTW-R在节省时间的同时，还能保持较高的分类准确率。

图4 DTW与DTW-R特征在不同交叉验证下的运算时间对比Fig.4 Comparison of running time between Feature-CS-DTW and Feature-CS-DTW-R with different fold cross verification

图5 3种数据集上DTW与DTW-R的性能对比Fig.5 Performance comparison between Feature-CS-DTW and Feature-CS-DTW-R on three data sets

最后，将结合DTW-R提取的特征映射到二维空间[3]，以灰色圆圈表示分泌蛋白，黑色叉号表示非分泌蛋白，画出数据分布图如图6所示。可以清楚看到，两组数据很容易被区分开来，并且圆圈和叉号的分布都比较集中。特别地，所有分泌蛋白都被划分在一个较为紧密的区域，只有少数非分泌蛋白被错误地分成了分泌蛋白，而分泌蛋白并没有被错误地划分为非分泌蛋白。说明根据新方法提取的特征向量具有较好的可鉴别性。

图6 算法的区分效果图Fig.6 Classification of the algorithm

3 结束语

本文结合压缩感知技术和动态时间规整算法提出了一种特征提取的新算法，提高了识别信号肽的分类准确率，并进一步利用带限制窗的动态时间规整方法提高算法的计算速度。首先利用马尔可夫转移频次矩阵将原始符号序列转化成用数字表示的特征向量，该向量反映了由前一个氨基酸到后一个氨基酸的转移过程，也一定程度上描述了生物序列的二肽表示信息。接着利用压缩感知技术将稀疏数据映射到高密度的空间以降低冗余信息，提高分类准确率。最后通过压缩感知算法将特征向量进行时间维度以标准形式表示。通过在多组数据集上进行实验验证，结果显示利用该方法提取的特征向量较氨基酸组分、尺度小波分析法以及单纯的使用压缩感知技术所得到的特征向量具有更好的鉴别性。这是因为新的特征向量既体现信号肽中的氨基酸组成、排列顺序、结构等重要结构信息，又能把信号肽的不同区域在时间维度中非线性地弯曲对整，以克服信号肽序列长度的不同，从而得到了比较准确的特征表达。新方法提取的特征向量在3个数据集Eukaryotes,Gram+bacteria,Gram-bacteria上的识别率分别达到99.32%,97.32%和98.67%，而使用氨基酸组分成分的识别率分别是78.91%,68.48%和58.72%，使用尺度小波分析法的识别率分别是93.40%,88.59%和88.06%，使用神经网络的识别率分别是71.8%,66.9%和81.7%[20]，使用隐马尔可夫模型的识别率分别是69.5%,64.5%和81.4%[20]。可以看出该方法在数据样本个数较少的数据集上，信号肽识别效果优于其他传统方法。

值得注意的是，本文方法依然存在一些不足之处。对不同的数据集使用本文方法最后得到的特征向量的维度一般来说是不相同的，它是由入选为训练集的数据样本个数来确定的。例如使用十重交叉验证的话，该维度便是样本总数的1/10，因此数据维度会随着样本总数的增加而变大，当样本总数特别大的时候该算法的计算效率通常会很低。

本文下一步研究方向主要包括两个方面：一个是关于压缩感知技术的压缩维度的确定，现有的文献没有对此进行深入的研究和探讨，目前已知的是压缩维度的选择不会很大程度地影响最后的分类准确率[2]。本文的数据集实验结果证明了此结论，即使是最极端的令压缩维度为1的情况下。另一个是DTW-R的参数R（限制窗口的大小）的选择，目前采取的是默认的10%[17]，如若优化参数R将进一步提高分类准确率。