离心泵多目标优化设计及数值模拟研究

董 敏，杨 浩，陈铁桩

(燕山大学机械工程学院，河北 秦皇岛 066004)

离心泵是一种通用机械设备[1]，主要用于流体的加压输送作业，液体在泵内流动由叶轮旋转提供动力，由于叶轮的运动形式，泵的大多数故障都与叶轮有关，比如发生汽蚀、泵体工作时剧烈振动[2]等，作为离心泵的一个重要部件，叶轮的设计水平对离心泵的正常平稳工作有重要的意义。

离心泵的优化过程是由很多因素决定的，分析了以往的优化方案，大多数都是以单目标优化为主，比如以离心泵的能量损失最小为优化目标，虽然提高了工作效率，但往往会忽略泵的汽蚀余量，造成抗气蚀性能性能下降，所以采用单目标优化方法对泵的整体优化水平提高有一定限制[3]。当前，很多学者研究了多目标优化方法在离心泵优化设计方面的应用[4,5]，并将传统数学模型与优化算法相结合，在这方面取得的成果有很多。本文以离心泵的能量损失、汽蚀性能、运行稳定性这3个指标为目标函数，分别建立离心泵能量损失、汽蚀余量最小以及避免出现驼峰曲3个数学模型，采用权矩阵分析的方法[6]，给3个分目标函数分配相应的权值，并通过评价函数将它们统一为一个目标函数，最后将优化模型与优化算法结合，在各个设计参数的取值范围内求出它们最优组合，使目标函数能达到最优解。同时，利用CFX软件对水体模型做数值模拟分析，了解优化前后流场中的压力脉动情况[7-10]。为了提高离心泵的优化水平，需要尽可能多地考虑优化设计变量对整体的影响，本文选择了离心泵叶轮水力设计中影响较大的7个设计变量，具体为：叶轮出口直径D2、叶片出口宽度b2、叶片出口安放角β2、叶片进口直径D1、叶片进口宽度b1、叶片进口安放角β1、叶片数z，其他设计参数由于对离心泵的水力性能影响很小，可以依据经验公式选取。

X=[x1，x2，x3，x4，x5，x6，x7]T=[D2，b2β2，D1，b1，β1，z]T

(1)

1 优化模型

本文在进行优化计算所采用模型泵为一台低比转速离心泵，型号为IB65-40-200，性能参数如表1所示。

表1 离心泵性能参数

1.1 能量损失模型

流体在泵中流动时，主要有机械损失、容积损失和水力损失，因此离心泵内部的能量损失可以有下式表示：

P=Pm+Pv+Ph=Pm+ρgqHt+ρgQ(Ht-H)

(2)

式中：Pm为机械损失，W；PV为容积损失，W；Ph为水力损失，W。

(1)机械损失。离心泵的机械损失主要是两部分：液体与叶轮之间的机械摩擦损失[11]Pm1，泵的轴承和填料函中的机械摩擦损失Pm2，总的机械损失[12]为：

(3)

式中：ρ为泵输送液体的密度，kg/m3；g为重力加速度，m/s2；u2为叶轮出口圆周角速度，m/s；D2为叶轮出口直径，m；Q为泵的实际流量，m3/s；H为泵的实际扬程，m；η为泵的机械效率。

(2)容积损失。

Pv=ρgqHt

(4)

(5)

式中：Ht为泵的理论扬程[13]，m；q为液体泄漏量[12]，m3/s；Ψ2为出口滑移系数取Ψ2=0.85；Z为叶片数；Qt为泵的理论流量，m3/s；n为叶轮转数，r/min；β2为叶片出口安放角。

(3)水力损失。

Pv=ρgQ(Ht-H)

(6)

综上所述，离心泵的能量损失最小的目标函数可以写成如下形式：

f1(x)=min(Pm+Pv+Ph)

(7)

1.2 泵的汽蚀余量

泵的汽蚀余量[14]由下式表示：

(8)

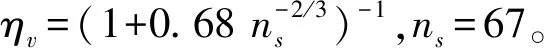
离心泵的汽蚀余量最小的目标函数可以写成如下形式：

f2(x)=min (NPSHr)

(9)

1.3 泵的稳定性目标函数

通过消除流量-扬程特性曲线的“驼峰”现象，建立离心泵的稳定性数学模型。从离心泵的理论扬程基本公式能看出，当流量Q增大时，理论扬程Ht减小，Ht～Q曲线形状为一条单调下降直线。同时，H～Q曲线也应该呈单调下降趋势，即一个扬程值对应一个流量值，实际上由于各种能量损失的存在，在某些条件下，H～Q曲线不呈单调性，曲线形状会出现“驼峰”现象，即同一个扬程值对应着两个或三个流量值，这种情况下，泵往往会出现不稳定的工作状态，所以，避免H～Q曲线出现“驼峰”，可以作为提高离心泵工作稳定性的依据。图1为离心泵的特性曲线分析。H～Q曲线形状由Ht～Q曲线和各种能量损失决定，当Ht～Q曲线斜率越大，H～Q曲线形状越陡峭，越不容易出现“驼峰”现象，泵的理论扬程曲线斜率可由下式表示：

(10)

离心泵的稳定性目标函数可以写成如下形式：

(11)

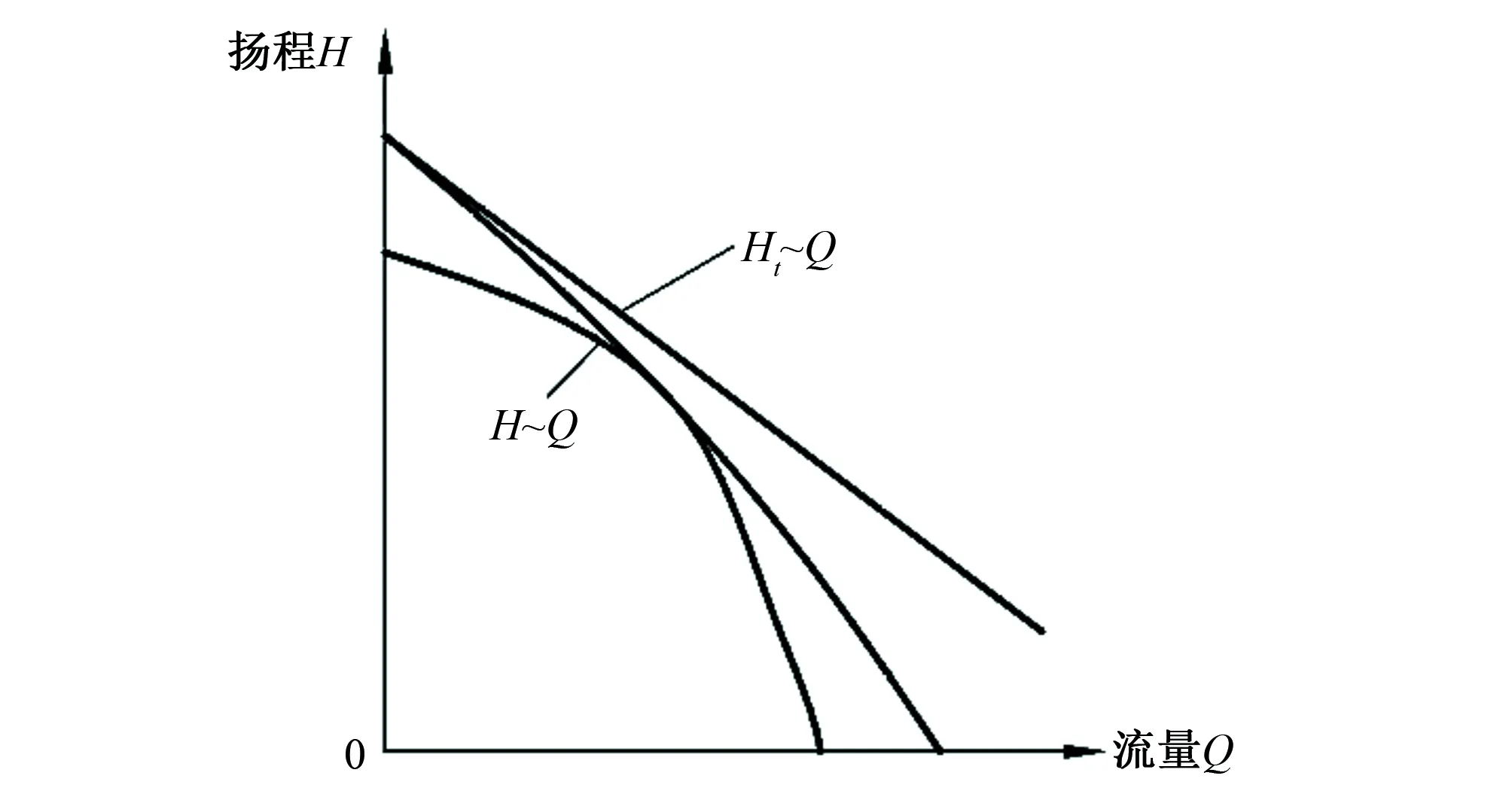
图1 离心泵的特性曲线分析

1.4 多目标优化模型权值确定

多目标优化设计中经常根据各分目标函数的重要性分别赋予相应的权值，然后采用统一目标法将各个分目标函数合并成一个整体，权值赋予的是否准确，往往对优化结果产生很大的影响，以往有些方法是依据设计经验给出各分目标的初始权值，这种方法虽然使用方便，但求解过程中有很大的随机性，不能准确的反映各分目标函数的重要性，为了进一步提高各分目标函数权值计算的准确性，本文采用运筹学理论中的权矩阵分析方法，求解各分目标函数的权重系数。

首先根据传统离心泵的设计经验，确定离心泵工作中能量损失的重要性是抗气蚀性能和稳定性的3倍，抗气蚀性能是稳定性的1.5倍。然后通过两两比较构建泵的能量损失、汽蚀余量和稳定性之间的二元比较矩阵，并转化为超传递矩阵，最后求出该矩阵最大特征值对应的特征向量，通过归一化处理得到各分目标函数相应的权重系数。

构建的二元比较矩阵为：

(12)

转化为超传递近似矩阵为：

(13)

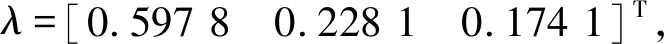
根据求得的权重系数将多个目标函数数学模型转化为一个单目标的函数，从而将多目标优化问题转换成单目标优化问题。则总的优化目标函数为：

minf(x)=0.597 8f1(x)+0.228 1f2(x)+0.174 1f3(x)

(14)

2 多目标优化过程及结果

根据上面建立的数学模型，选择遗传算法进行多目标优化，其主要优点是具有良好的全局搜索能力，将每一步的优化结果转换成适应度值，根据适应度值确定下一步的优化方向，这样能迅速从变量的取值范围内找出参数的最优组合，避免产生局部最优解。由于设计变量的取值范围对优化过程非常重要，只有范围取得合理才能得到比较准确的优化结果，本文在参考了大量优秀泵的设计经验基础上确定了叶轮设计变量的取值范围(见表2)。

选择使用MATLAB中的遗传算法工具箱(GA Tool)进行优化计算，将设计变量取值范围代入，求得的优化后结果与优化前结果进行对比，如表3所示。

将优化后的叶轮几何参数反代入离心泵能量损失方程式，得出优化后的能量损失为2 444.4 W，与优化前相比降低了4.3%，汽蚀余量由优化前3.27 m降低为2.96 m，为保证离心泵运行的稳定性，需要尽可能增大H～Q曲线斜率，从上面理论扬程方程式来看，减小叶片出口宽度、叶片出口安放角都能达到增加曲线斜率的目的，观察优化后的结果，确实满足这个规律。

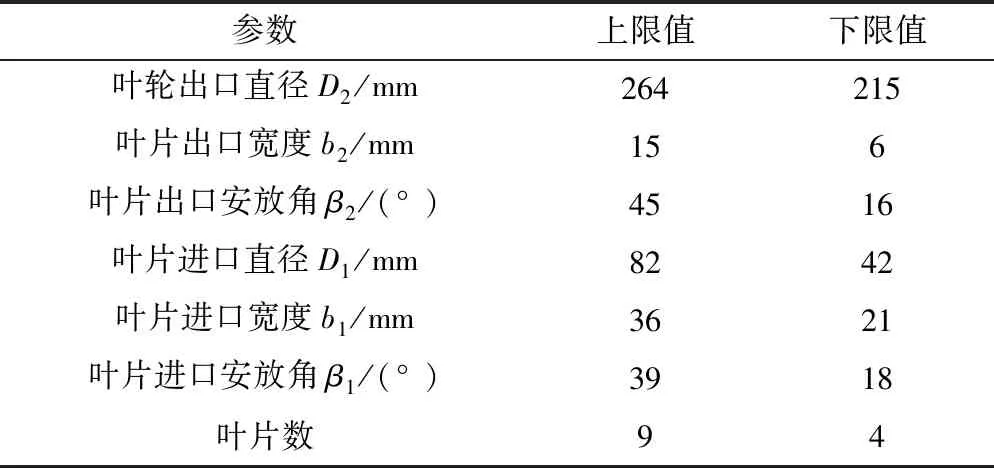
表2 叶轮参数取值范围

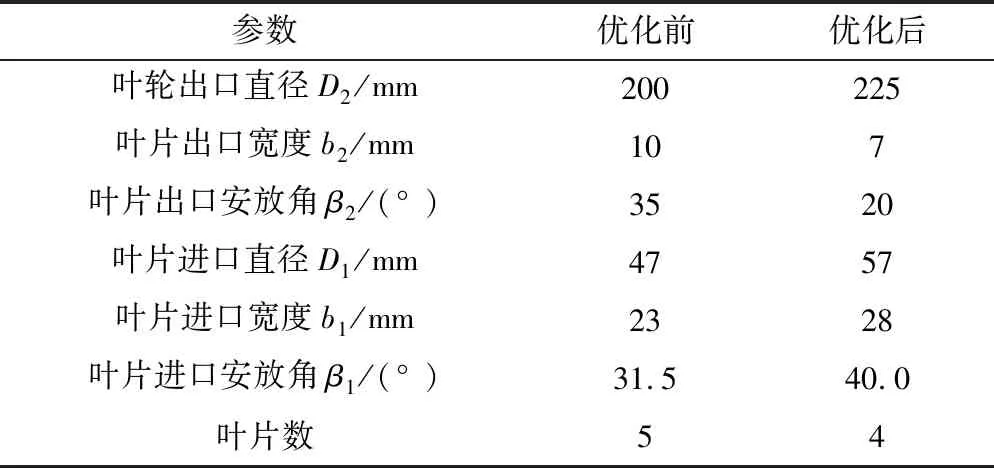
表3 叶轮参数优化前后对比

3 数值模拟分析

将消除H～Q曲线“驼峰”现象作为改善离心泵工作稳定性的优化数学模型，计算结果的可行性需要进一步验证，对流场进行数值模拟分析，可以了解泵内流场的压力分布状态及变化情况，如果流场的压力值变化剧烈，说明离心泵内流体的流动状态不稳定，代表着离心泵的工作状态也不平稳，所以将优化前后泵内流场的压力脉动幅值波动情况进行对比，可以作为离心泵工作稳定性是否得到改善的依据。

3.1 建立三维模型

根据优化后的叶轮参数建立了对应的离心泵水体模型，利用ANSYS CFX软件对泵的水体模型进行数值模拟，获得液体在流道内的流动状态及压力变化情况，将数值模拟方案的仿真结果与数学优化模型进行对比，进一步验证优化结果的可靠性。为了使进入泵内的液体有相对稳定的流态，提高数值模拟的精度，在泵的进口添加一段圆柱形进口管，进口管的长度为管径的2.5倍，图2为离心泵的水体三维模型。

图2 离心泵水体三维模型

3.2 划分网格

为了方便利用控制方程对模型进行求解，使用ICEM CFD软件对泵的水体模型作非结构化网格划分，这样整个计算域就可以分成多个便于求解的小单元，其中，进口管、叶轮、蜗壳都选择划分效果较好的四面体网格类型，为提高网格的划分质量，对隔舌及叶片进口段网格进行局部加密，最终叶轮、进口管、蜗壳网格数为773 662、1 363 112、1 332 196。

3.3 监测点设置

在蜗壳流道内设置压力监测点记录动态压力信息，监测点分布在蜗壳流道中截面的圆周上，距离叶轮出口的距离都为2 mm，在整个计算域中选择了三处有代表性的位置，其中，P1设置在隔舌面，P2、P3设置在蜗壳流道的第Ⅲ和第Ⅴ断面位置，监测点位置如图3所示。

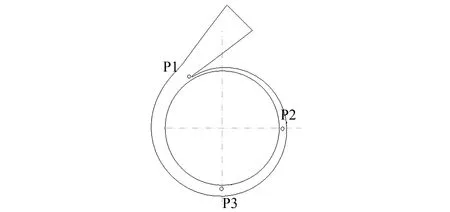
图3 监测点位置示意图

采用CFX软件对泵的水体模型进行定常及非定常计算，在定常求解的3个计算域中，叶轮属于旋转域，进口管、蜗壳属于静止域， 所有固体壁面取无滑移壁面条件，进口边界条件设置为总压(Total Pressure)，出口边界设置为质量流(Mass Flow Rate)，本文中的模型进口压力设置为1 atm，根据泵出口的流量，出口质量设置为12.7 kg/s，湍流模型选择k-Epsilon模型。对于叶轮这类旋转类部件，计算域属性选择旋转域，蜗壳及进口管的属性选择静止域，计算域的壁面条件都假设为无滑移，表面粗糙度定为0.025 mm。为了得到蜗壳流道内某一时刻压力的分布状况，在定常求解的基础上对泵的流场作非定常求解，总时间(Total Time)设为0.124 138 s，该时间为叶轮转过6圈所用的时间，后处理可以选择达到相对稳定的第6周期数据进行分析，时间步长(Time Steps)设置为1.724×10-4s，即在这段时间内叶轮转过的角度为3°，将平均残差作为判断的收敛条件，其值设为10-4。

3.4 监测点处的压力脉动

图4分别根据在监测点P1、P2、P3处采集的压力数据而生成的压力脉动时域曲线图，从图4可以发现，叶轮旋转一周，压力脉动曲线都出现了4个周期，图4显示的波峰数与叶轮的叶片数目保持一致，这说明叶轮与蜗壳之间的相互作用，对流道内的压力变化有很大影响。

图4 P1、P2和P3监测点压力脉动时域图

图4(a)为监测点P1处优化前后蜗壳流道内的压力脉动曲线图，由P1的位置可知其处于蜗壳的隔舌面上，分别和图4(b)和图4(c)中脉动曲线对比，可以观察到，监测点P1处的曲线波动比监测点P2、P3处的曲线波动更强烈，而且还出现了明显的次波峰，说明隔舌附近区域的压力变化比蜗壳流道其他区域更明显，这主要是因为隔舌附近区域流场受叶轮与蜗壳的干涉作用更明显，该位置的流体产生了相对于其他区域更不稳定的流动。对比优化前后的压力脉动情况，优化后的压力脉动幅值小于优化前的脉动幅值，且优化后脉动曲线的次波峰强度出现了一定的降低，说明优化过程改善了隔舌附近流场的压力波动情况，提高了泵运行过程中的稳定性。

图4(b)和图4(c)为监测点P2和P3处的压力脉动曲线图，对比两个监测点处的曲线发现，可以看到图4(b)的曲线有次波峰出现，说明该监测点处的压力变化比P3处的更明显，根据监测点的位置可知，P2点相对于P3点离隔舌更近，更容易受叶片扫过隔舌时产生的“尾迹”影响，所以压力变化更加明显。优化后的叶轮方案中，P2和P3处的压力脉动幅值都比优化前出现了明显的降低，结合P1处的脉动幅值变化情况，可以进一步证明，经过优化后，离心泵的运行稳定性有了一定程度的提高。

4 结 语

采用多目标优化与数值模拟相结合的方法，对一台低比转速离心泵进行优化分析，结果表明：

(1)优化后的模型泵能量损失降低了4.3%，汽蚀余量降低了0.31 m，证明了建立的优化模型符合实际设计要求，基于权矩阵分析法确定的权重因子选择合理可靠。

(2)在提高离心泵工作稳定性的优化数学模型中，将增大离心泵的理论扬程曲线斜率作为优化的方向，随后对流场进行数值模拟，根据流场内的压力脉动幅值变化情况对优化结果进行验证，结果显示：优化后，离心泵蜗壳流道内的压力脉动幅值出现了明显的降低，内部流场的流动状态比优化前有一定改善，工作时运行稳定性得到了提高。