基于Copula函数的叶尔羌河流域洪水要素联合分布研究

何 英 ，彭 亮，郑淑文，马林潇

(新疆农业大学水利与土木工程学院，乌鲁木齐 830052)

近年来，用Copula函数进行洪水过程分析成为水文计算领域的一个研究热点[1]，杨卫等选用Gumbel、Clayton和Frank 3种Copula函数建立降雨-洪量极值联合分布模型[2]；范嘉炜等基于Copula函数分析了潖江河大庙峡流域洪峰流量与洪水历时的联合频率分布特征[3]；侯芸芸以陕北地区洪水资料为研究对象，运用Copula函数建立了洪水特征变量的联合概率分布和条件概率分布模型[4]；张冬冬等应用Archimedean Copula函数探讨洪水多要素的联合概率分布和条件概率分布[5]；高玉琴等应用Gumbel-Hougaard Copula函数进行秦淮河流域洪水风险分析[6]；李天元等采用金沙江屏山站和岷江高场站的日径流资料，探讨了双参数Archimedean Copula函数在洪水联合分布中的应用[6]；林娴等基于Copula函数原理，利用武江流域实测水文资料，构建了流域组合变量Copula概率分布模型，分析了洪峰与洪量、洪量与洪水历时、洪峰与洪水历时的联合概率分布[7]；李大鸣等采用阿基米德Gumbel-Hougaard Copula函数，构建了入库洪峰与洪量的两变量联合分布模型，对桃林口水库进行防洪风险分析[8]，姚瑞虎等基于Copula函数论述并推求了四种洪水重现期的理念及其计算，并以岷江支流马边河马边水文站为例，对比分析各重现期之间的关系[9]。

本文以叶尔羌河流域为例，利用卡群水文站实测水文资料，基于洪峰和洪量均服从P-Ⅲ型分布，应用Archimedean Copula函数，探讨叶尔羌河流域洪峰、洪量联合概率分布模型，以期为水利工程规划设计和风险评估提供科学依据。

1 数据与方法

1.1 研究区域与数据来源

1.1.1 研究区域

叶尔羌，维吾尔语中意为“土地宽广的地方”。叶尔羌河是塔里木河四源之一，位于中国最西部的新疆维吾尔自治区内。汹涌的山区急流出了昆仑峡谷后向北流，形成许多分支，散布在冲积扇上，灌溉着叶尔羌绿洲；叶尔羌绿洲是新疆最大的绿洲之一，流出绿洲后的叶尔羌河绕过塔克拉玛干沙漠西缘，流向东北，在阿克苏绿洲南部汇集喀什噶尔河、阿克苏河及和田河，形成塔里木河，是喀什地区的第一大河流。河流全长1 179 km，水源一是来自乔戈里峰的冰雪融水；二是河床西岸岩层中涌出的泉水；三是雨水，多年平均年径流量75.71 亿m3，年均向塔里木河输水1.7 亿m3，灌溉塔什库尔干、叶城、泽普、莎车、麦盖提、巴楚6个县和农三师10个团场共28.889 万hm2耕地。叶尔羌河流域面积为10.8 万km2，属干旱性内陆气候区，降水少，蒸发强烈，多年平均降水量仅为55 mm左右，多年平均蒸发量为2 400 mm左右。区内干旱、沙暴、洪水等灾害发生较频繁，自然生态环境脆弱，流域地理位置示意图见图1。

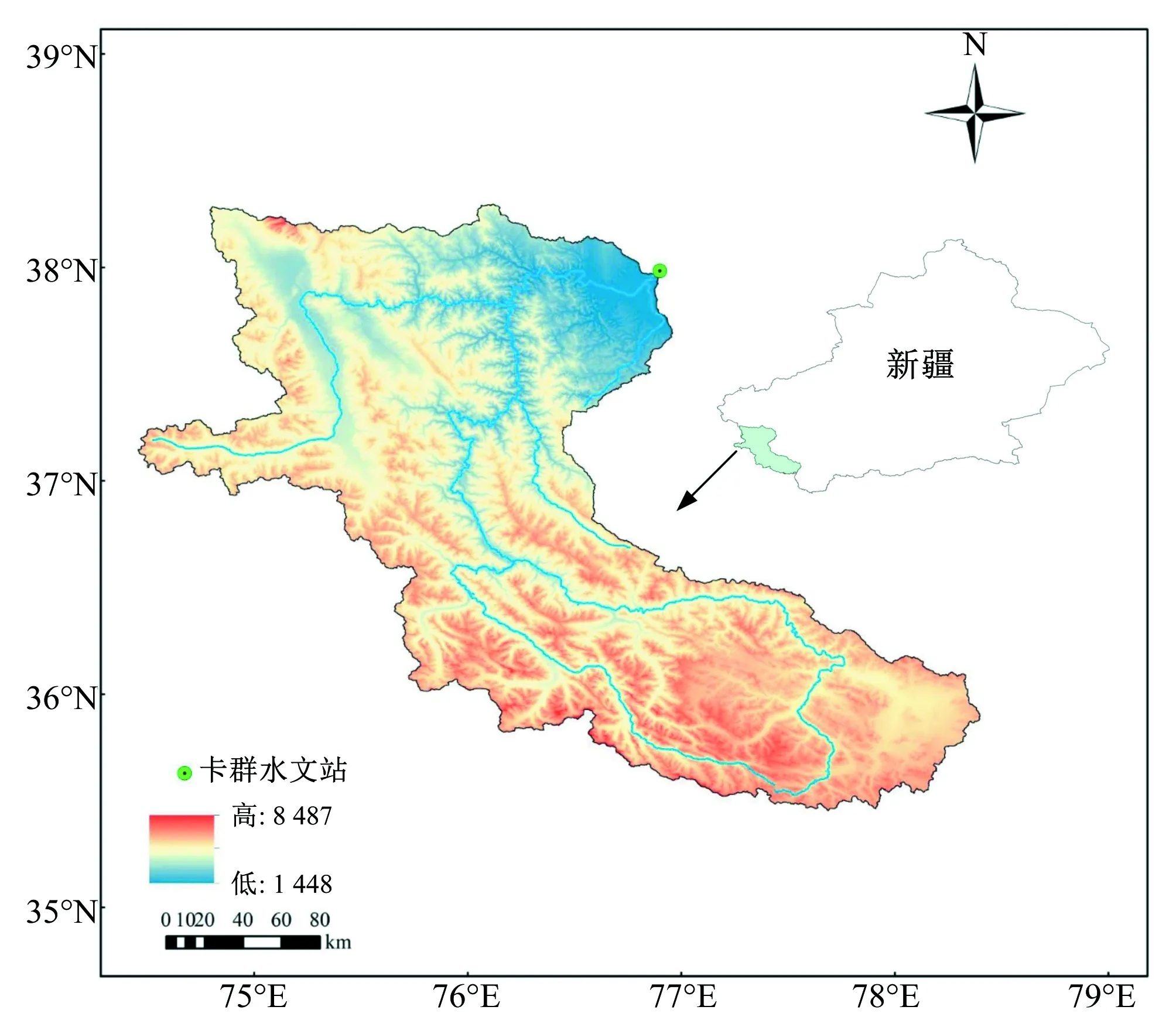
图1 叶尔羌河流域地理位置示意图Fig.1 Geographical location schematic diagram of the Yeerqiang River Basin

1.1.2 数据来源及资料代表性分析

本文研究主要采用叶尔羌河流域卡群水文站1954-2011年共58 a 日流量资料，采用年最大值选样法(AM)，选取该水文站的年最大洪水所对应的洪峰流量、1日洪水总量为研究变量，运用Coupla函数对叶尔羌河流域卡群水文站站址处洪水要素进行联合分布研究。

绘制卡群水文站洪峰流量模比系数差积曲线见图2。由图2可以看出，卡群水文站实测洪水系列中包含了较完整的涨落水过程，所以，卡群水文站58 a的最大洪峰流量样本系列包括有丰、平、枯各种年份，具有较好的代表性。

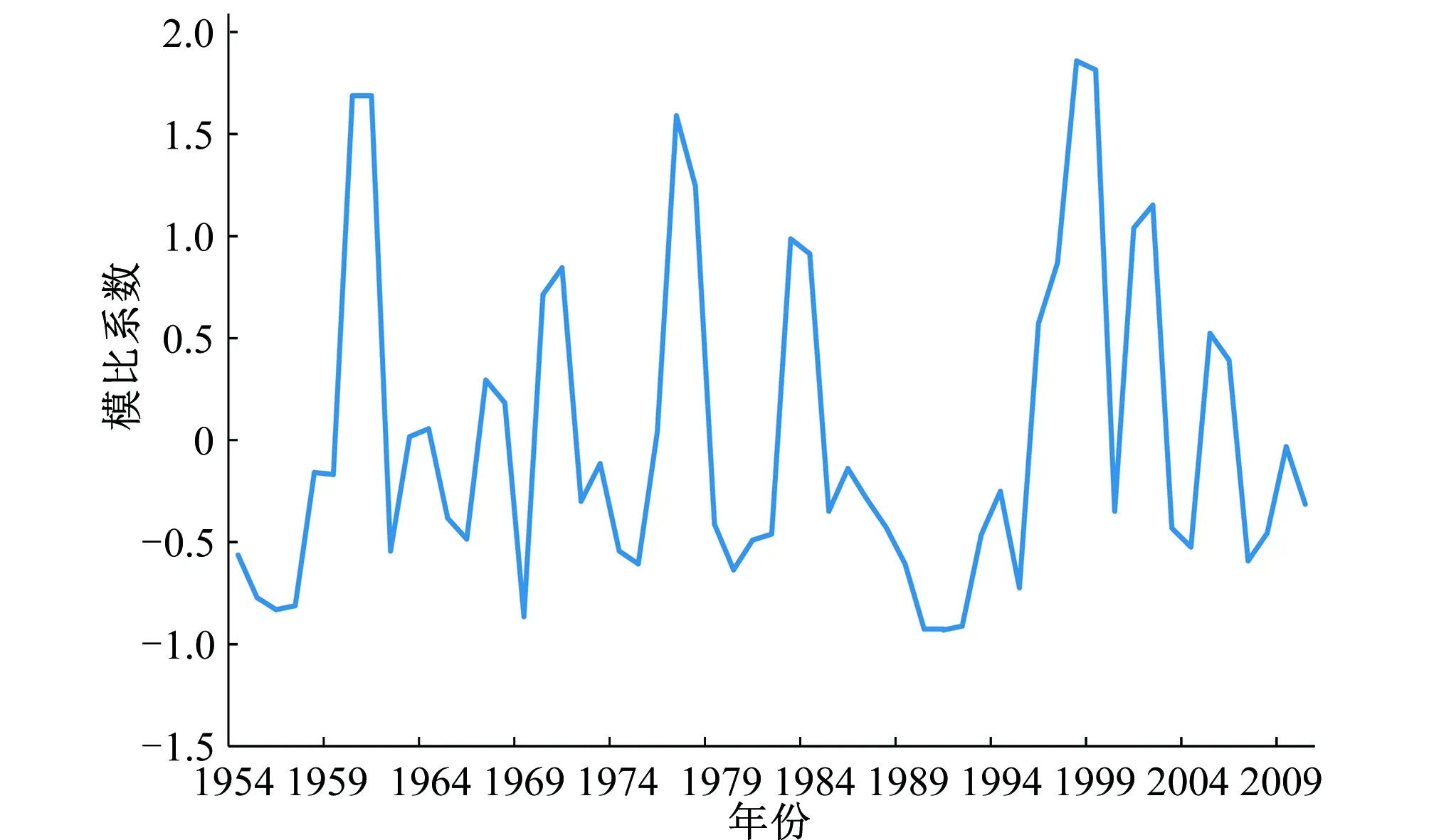
图2 卡群水文站洪峰流量模比系数差积曲线Fig.2 The difference product curve of flood peak flow modulus coefficient in Kaqun hydro-logical station

1.2 边缘分布函数

P-Ⅲ型分布常用来模拟降水量、径流量或洪峰流量等，其概率密度函数见公式(1)，P-Ⅲ分布参数可选用线性矩法进行估计，通过对样本参数的无偏估计，便可得出P-Ⅲ曲线的参数：

(1)

(2)

(3)

式中：α、β、a0分别为P-Ⅲ分布的形状、尺度和位置参数；Γ(·)为伽马函数。

1.3 Copula函数与参数估计

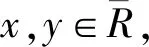
H(x,y)=C[F(x),G(y)]

(4)

如果F和G是连续的，则C是唯一的。否则，C在RanF×RanG上(Ran表示值域)唯一确定。多种Coupla函数都可应用于建立水文变量的多维联合分布。其中Archimedean Copula函数结构简单，计算简便，可以构造出形式多样、适应性强的多变量联合分布函数，能够满足大多数领域的应用要求，在实际应用中占有很重要的地位。常用的二维Archimedean Copula函数主要包括：Gumbel-Hougaard(G-H) Copula、Clayton Copula、Ali-Mikhail-Haq(AMH)Copula、Frank Copula，Nelson[9]对Archimedean Copula函数及其性质进行了详细的介绍，见表1。

表1 函数类型与参数Tab.1 Function types and parameters

估计Copula函数参数的方法有多种，本文采用Kendall相关系数法[10]对Copula函数中的参数α进行估计。建立Kendall秩相关系数τ与α的关系，见表1，其中Kendall秩相关系数表示为：

(5)

式中：τ为秩相关系数；(xi，yi)为测点据；sgn(·)为符号函数，n为系列长度。

由实测资料计算得到Kendall秩相关系数后，可以很容易地求得Copula函数的参数α。

1.4 拟合优度评价

在运用Archimedean Copula函数研究实际问题的过程中，为选择合理的Copula函数来正确描述变量间相关结构，需要对各函数进行拟合度评价和检验。常见检验方法有均方根误差RMSE法、AIC信息准则法、Genest-Rivest图形分析法。

(1)均方根误差RMSE法。Yue等最先采用基于理论值与实测值的拟合曲线来直观地检验多维分布的拟合情况[11,12]。而后Beersma和Buishand开始将该方法用于Copula函数的拟合检验[13]。Zhang和Singh基于该方法，通过计算理论值和实测值的均方根误差RMSE，定量地评估了拟合误差大小。RMSE的计算公式为[14]：

(6)

式中：E为数学期望；N为样本容量；pc为实测概率值；p0为Copula函数计算得到的理论概率值。

(2)AIC信息准则法。Zhang和Singh引入AIC指标(Akaike’s information criterion)，用于选择合适的Copula函数[15]，其计算公式为：

AIC=Nln(MSE)+2k

(7)

式中：k是Copula函数参数的个数；AIC值越小证明拟合效果越好。

(3)Genest-Rivest图形分析法。Genest-Rivest图形分析法是Genest和Rivest提出的一种评价Copula函数拟合效果的方法，分别计算理论估计值Kc(t)和Ke(t)，然后点绘Kc(t)和Ke(t)关系图，如果图上的点都落在45°对角线上，那么表明Kc(t)和Ke(t)完全相等，即Copula函数拟合得很好[16]。

1.5 联合分布重现期

在洪水频率分析计算时，我们更关心的是洪峰、洪水总量等洪水变量超过某一特定值或者洪水多要素共同超过某一特定值时的频率，即重现期。设FX(x)和FY(y)分别为洪水特征变量X和Y的分布函数，两变量同时超过某一特定值的重现期如下式所示。

(8)

两变量中任一变量超过某一特定值时的重现期如式(9)所示。

(9)

其中用Txy记T(X>x,Y>y)；用Tx/y记T(X>xorY>y)。

2 结果与讨论

2.1 洪水特征变量的边缘分布

运用矩法公式(3)初步估计洪峰、最大1日洪量服从的P-Ⅲ分布函数的参数值，可得洪峰和最大1日洪量的统计参数，以AIC准则为依据，通过计算机适线法得到卡群水文站洪峰流量、最大1日洪量频率曲线。洪峰流量采用Q均值=2 052.59 m3/s，Cv=0.62，Cs/Cv=4.5；最大1日洪量采用W均值=1.228 亿m3，Cv=0.32，Cs/Cv=5。绘制变量边际分布经验频率与理论频率关系图，如图3所示，由图3可以看出，点据均分布在1∶1斜线附近，洪峰流量相关方程为y=0.839 2x+0.043 4，相关系数R2为0.971 2；洪水总量相关方程为y=0.999 4x+0.016，相关系数R2为0.977 8；证明拟合程度较好。

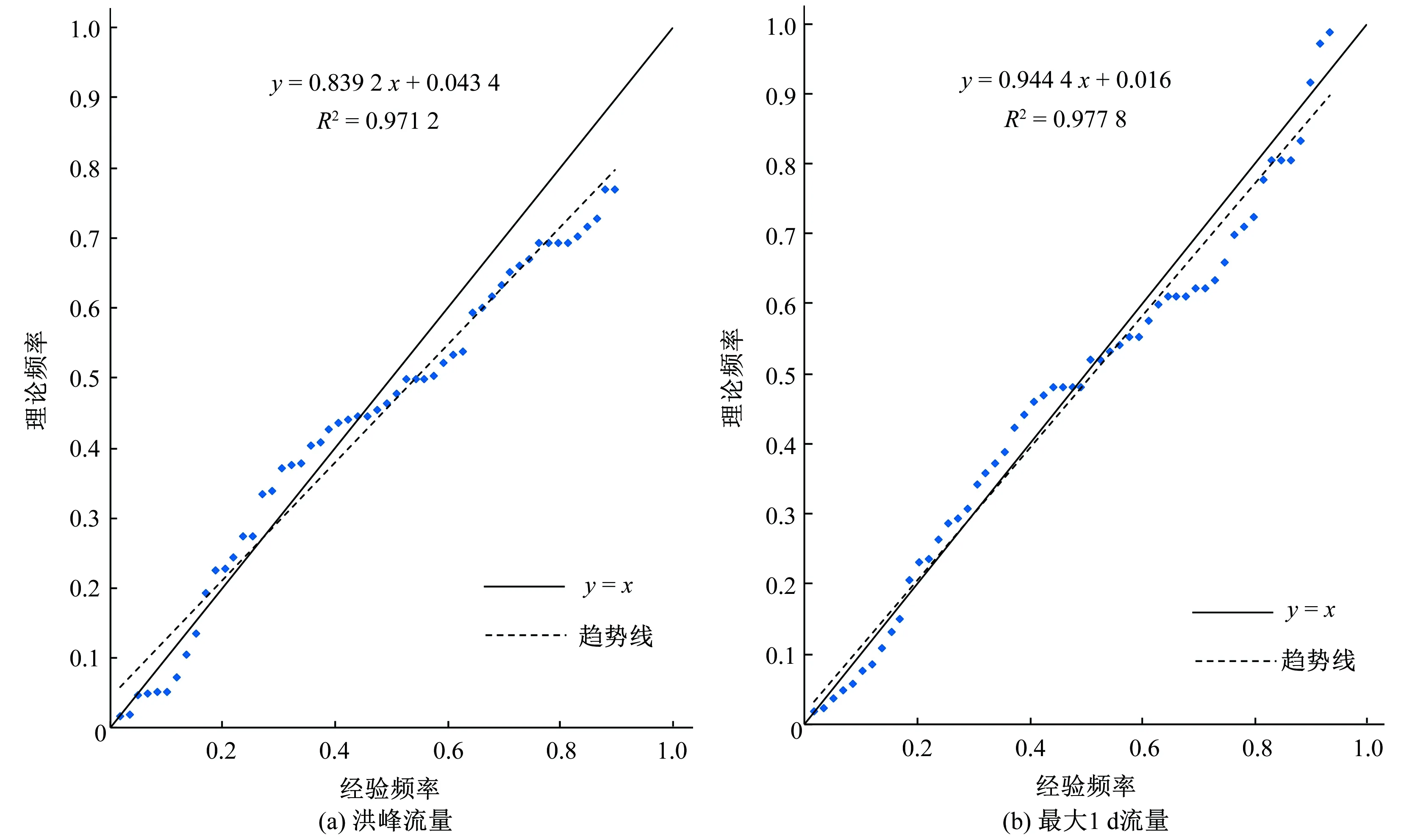
图3 边缘分布拟合图Fig.3 Marginal distribution fitting map

2.2 Copula函数参数估计及拟合优度检验

本文选择Copula函数中常见的4种二维Archimedean Copula函数进行参数估计，并从中选择最优函数拟合变量。采用Pearson′γ，Spearman′ρ和Kendall′τ进行洪峰和洪量间的相依性度量，经计算γ=0.83，ρ=0.68，τ=0.57，说明洪峰与洪量之间存在较强相关性，因而可进行洪水变量间的联合概率特性分析。

各Copula函数的参数估计值及拟合优度检验指标列于表2，图4 为几种Copula函数的Kc～Ke关系图。表2中的REMS和AIC值显示，G-H Copula函数拟合最优，图4显示G-H Copula函数的Kc～Ke关系图上的点基本落于45°对角线附近，拟合效果优于其他3种常用的Archimedean Copula函数。

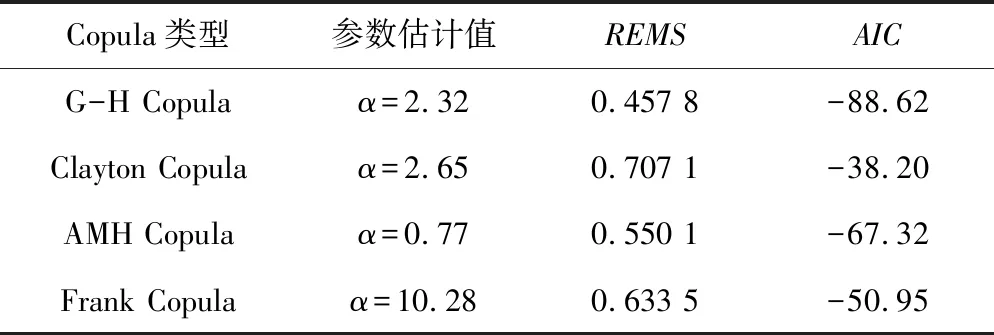
表2 Archimedean Copula函数参数估计及拟合优度检验指标Tab.2 Parameter estimation goodness of fit test indicator of Archimedean Copula function

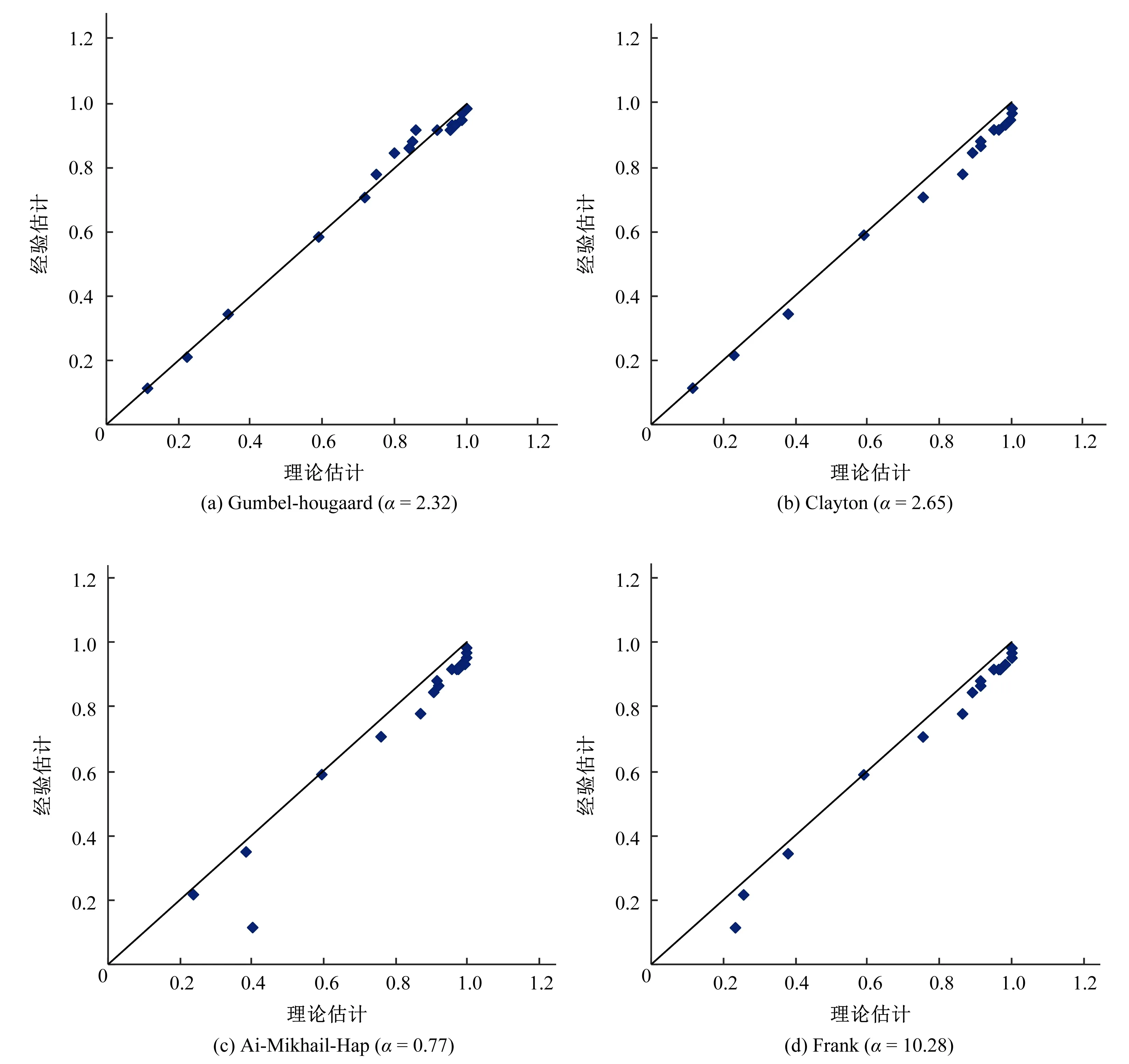
图4 Archimedean Copula函数Kc～Ke关系图Fig.4 Archimedean Copula function Kc～Ke diagram

2.3 组合变量分布函数与单变量分布函数对比分析

(1)同场洪水重现期结果对比。由前述拟合度优检验，可知叶尔羌河流域洪峰与洪量联合分布拟合最优的copula概率分布函数为Gumbel Copula函数，由Gumbel Copula联合概率分布函数即可推算出不同频率下的洪水特征值，利用Matlab绘图工具绘制参数α为2.32的Gumbel Copula的联合概率密度函数图和联合概率分布函数图(见图5)，由公式(8)和公式(9)可求得洪峰、洪量两变量组合下的联合重现期[T(x/y)]和同现重现期[T(xy)]，绘出两变量等值线图(见图6)，根据两变量联合分布重现期等值线图可得到两变量组合下的重现期。

由于组合洪水变量采用Gumbel Copula函数拟合，而单一洪水变量均采用P-Ⅲ曲线拟合，同场次洪水的重现期结果不一样。以1999年洪水为例，年最大洪峰流量为6 070 m3/s，一日最大洪量为2.29 亿m3，由图4和图5可得该场次洪水各要素联合分布概率及重现期如表3所示。如按单变量计算，发生洪峰流量为6 070 m3/s的大洪水重现期为51年，发生一日最大洪量为2.29 亿m3的重现期为44年，平均每44年发生如此大的洪水，显然是不符合实际的。按洪峰流量与一日最大洪量两变量联合分布计算，同时发生最大洪峰流量为6 070 m3/s，一日最大洪量为2.29 亿m3大洪水的重现期为182年，即平均每182年发生一次，较为合理。

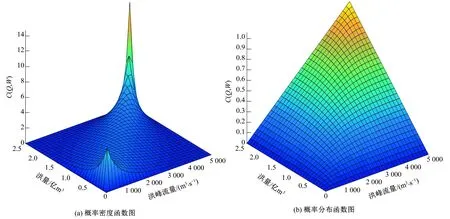
图5 两变量联合概率密度函数和分布函数图Fig.5 Probability density function and distribution function graph of two joint variable

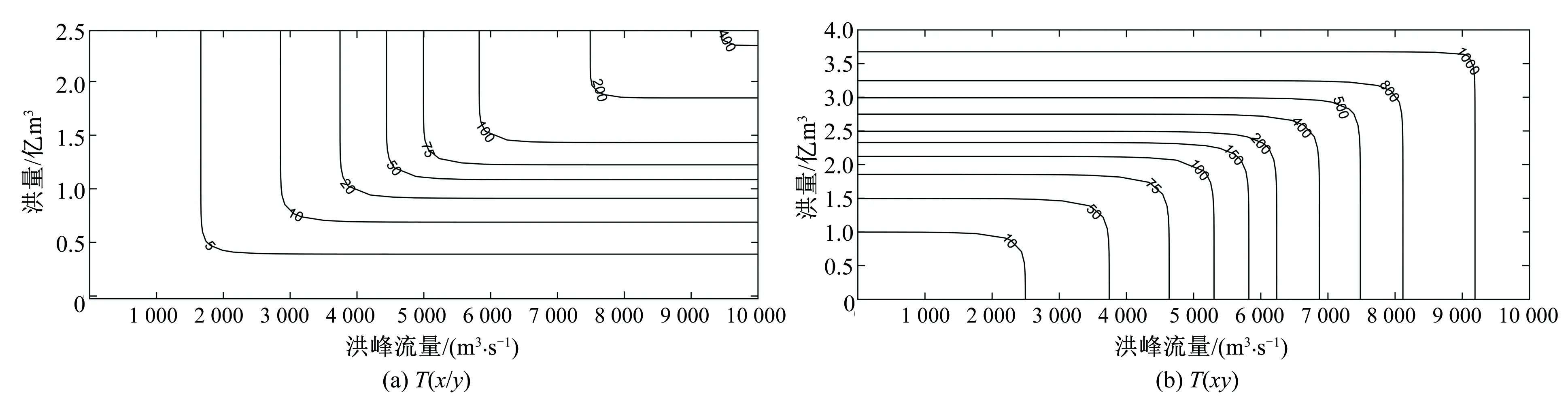
图6 两维联合分布重现期等值线平面图Fig.6 contour map of joint distribution recurrence period

表3 1999年场次洪水特征值联合分布重现期Tab.3 The recurrence period of flood eigenvalues joint distribution in 1999

由表3联合分布重现期计算结果可以看出，采用单一变量拟合分布函数时，该场次洪水洪峰流量的重现期为51年，洪量的重现期为44年；采用组合变量分布函数时，该场次洪水洪峰和洪量的联合重现期[T(x/y)](即相同大小的洪峰或洪量任一出现)为27年，同现重现期[T(xy)](即相同大小的洪峰和洪量同时出现)达182年。

(2)同重现期洪水参数对比。比较同一重现期下，单变量设计值与组合变量联合分布条件下设计值的不同。以叶尔羌河流域洪峰-洪量联合概率分布为例，统计分析了同一重现期下，单变量设计值与联合变量分布设计值的区别。由重现期计算公式反推出某一重现期下，叶尔羌河流域洪峰与洪量单变量设计值与联合变量分布设计值见表4。

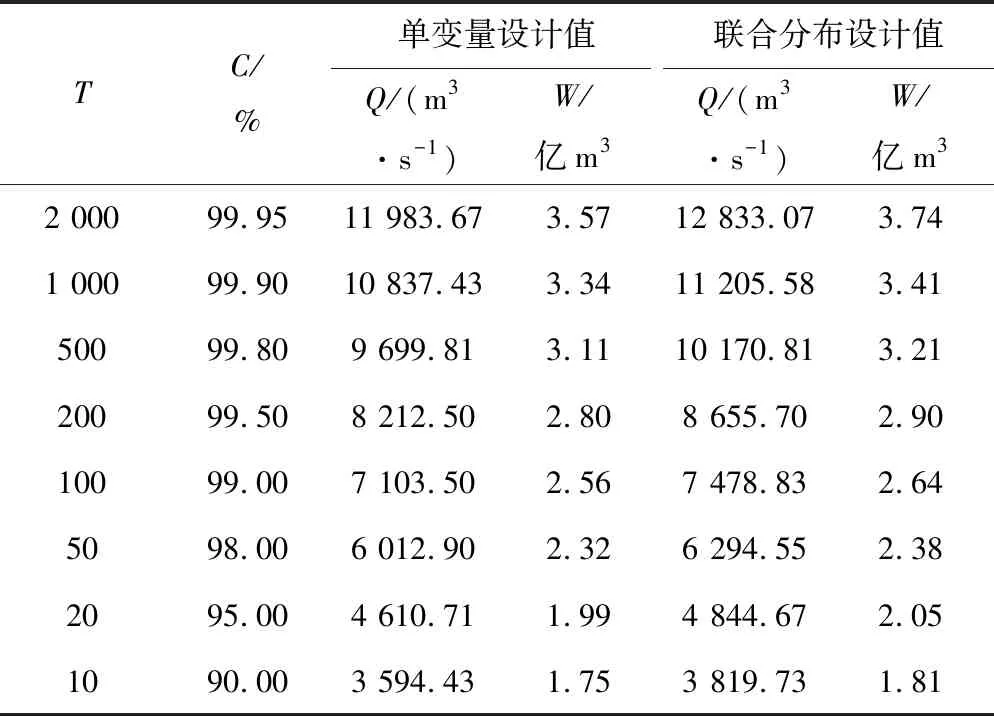
表4 单变量设计值与峰量联合分布下设计值Tab.4 Design value of single variable and joint distribution

由表4单变量设计值与峰量联合分布下设计值计算结果可知，对于百年一遇洪水，单变量分布函数洪峰和洪量设计值分别为7 103.5 m3/s和2.56 亿m3，而组合变量分布函数的设计值为7 478.83 m3/s和2.64 亿m3，由此可知，在同一重现期下，两变量联合分布法推求的洪峰流量和洪量设计值较单变量设计值偏大。

3 结 语

(1)本文对叶尔羌河卡群水文站历年水文资料进行代表性分析，认为卡群水文站具有较好的代表性。采用年最大法进行选样，提取洪峰流量与最大1日洪量相关信息，以皮尔逊Ⅲ型曲线为基础建立洪峰、洪量的单变量分布函数，绘制经验频率与理论频率关系图，得到洪峰流量相关方程为y=0.839 2x+0.043 4，相关系数R2为0.971 2；洪水总量相关方程为y=0.999 4x+0.016，相关系数R2为0.977 8；证明拟合程度较好。

(2)采用RMSE法、AIC信息准则法、Genest-Rivest图形分析法进行拟合优度评价，3种评价方法均得出一致的结果，认为Gumbel Copula函数拟合度最优，以此为基础建立基于Gumbel Copula函数的洪峰与洪量联合分布函数。

(3)采用MATLAB软件，利用Gumbel Copula联合概率分布函数推求了洪峰、洪量两变量组合下的联合重现期和同现重现期，绘制了洪峰、洪量组合下的联合分布图及两种重现期的等值线图，比较分析了同一重现期下，单变量设计值与组合变量联合分布条件下设计值的不同。结果显示联合分布时的设计值大于单变量设计值，即利用联合分布设计值对水利工程偏于安全。

由此可见，基于Copula函数的两变量联合分布的洪水频率分析方法能更好地描述洪水的特征，提供了分析变量间相互联系的大量信息，是单变量拟合所不具备的，且Copula函数对于边缘分布类型没有限制，大大增加了这种方法的实用性和推广性。本文研究结果可对未来叶尔羌河流域水利工程规划设计和风险评估工作提供参考依据。