基于MIKE和HEC-RAS模型模拟锦江水面线比较研究

蒋 楠，高 成

(河海大学水文水资源学院，南京 210098)

河道水面线的推求在河道水文及洪水预报方面已十分常见。其中山区天然河道水面线的推算大多和实际情况相差很大。而通过人工实时监测水位变化既耗时又费力。随着水文数值模拟计算技术的迅猛发展，数值仿真的对水文学的发展进步具有重要影响，并取得了一些可观的成果。例如MIKE11 和HEC-RAS模型就能够较为准确地推求出河段天然河道水面线，达到工程项目的预期效果。影响以上两个模型推求水面线结果的因素有很多，其中戴文鸿等[1]通过分析糙率公式得出糙率的变化对水面线的影响，但其还需对模型的节点概化以及边界条件设置等方面进行深入研究；蒋书伟、武永新[2]经过对以上两个模型的参数进行率定和验证，得出两个模型计算水面线具有一定可靠性。孔鲁志[3]介绍了MIKE11 以及HEC-RAS模型的计算原理，并将两者的水面线计算结果进行了对比，但对造成差异的原因并未进行深入研究；范威[4]应用HEC-RAS模型模拟了铁场河水面线，认为该模型比较适用于推求山区中小河流水面线。陈建峰等[7]介绍了HEC- RAS模型的结构和运行流程，并推求了黑河金盆水库坝址至入渭河口的河道洪水(P=1%)水面线，这对于防洪评价、洪泛区管理有较高实用价值；张涛等[9]应用MIKE11 一维水动力模型推算平原河道东鱼河水面线，并分析了河道水位～过水面积的关系，为洪水调度方式提供了参考依据，但未对模型参数的敏感性进行深入研究。

在以上研究基础上，本文主要研究应用HEC-RAS 和MIKE11模型推求河道水面线的过程，利用江西省高安市锦江流域不同设计标准的流量系列以及水文参数进行计算，并利用锦江河段的实测水位数据对计算结果验证分析，发现MIKE11模型具有更好的模拟效果，然后深入研究两个模型的计算结果的差异。考虑模型原理以及参与模型运行的主要水文参数糙率和初始水位，并对其进行敏感性分析，最后选择更加合适的软件进行锦江河道水面线计算，并可将此模型的运行结果应用于实际工程项目中。

1 研究方法

1.1 MIKE11模型原理

丹麦水资源研究所研发了MIKE模型系列，其中在水面线推求中最常用到的是由MIKE11和MIKE21。而MIKE11有多种模块可进行水文方面的计算，能用于各种类型的河道水面线模拟，它常常用于一维河道的水动力及水质、洪水风险分析和泥沙运输等工程项目。水动力模型(HD)是一维非恒定流计算中最重要的模块[4]，用来求解一维河道非恒定流方程的是Abott-Ionescu六点隐式差分格式。该模型已普遍应用于防洪、灌溉、河道水量水质评价以及溃坝分析等水利工程项目。

MIKE11一维河网汇流模型采用非恒定流圣维南(Saint-Venant)方程组构建。

连续方程：

(1)

动量方程：

(2)

式中：A为河道过水面积；Q为流量；t为时间；x为与水流方向一致的横向坐标；q为河道的侧向来流量；g为重力加速度；h为水位。

1.2 HEC-RAS模型原理

HEC-RAS也是一种常用于计算河道水面线的模型，可用于河道一维定流量和变流量的水动力计算。其应用领域较为广泛，可进行洪水水面线的计算、河道行洪能力以及河床冲淤等分析计算，可根据工程中河流的实际流态选择不同的控制方程对河道水面线进行推算。模型运行后，可生成过河道的水面线变化动态图、各个过水断面的形态图以及不同设计标准洪水的水位流量成果表等。

由于本次计算的是河道洪水过程，因此采用非恒定流方法即Newton-Raphson 迭代法计算水面线[5]。非恒定流计算的控制方程为动量方程和连续性方程，基本公式如下。

动量方程：

(3)

(4)

式中：ρ为水体密度；u为流速；f为质量力；υ为动力黏滞系数；P为压力。

2 研究区概况

江西省高安市地处该省中部偏西北，东距省城南昌市60 km，西距宜春市153 km，有“赣中明珠”之称。本次的研究对象为锦江桩号为K0+027到K3+856的一段河道。它的起源地是湘赣交界的幕阜山脉海拔高程为628.6 m的东麓坪子岭，河流流向自西向东，沿途流经宜春万载、宜丰、上高、高安、丰城、新建等县市，于南昌县市汊汇入赣江，集水区长而狭窄，地势从西北偏向东南方向，其山脉走向大多为东南向。全长304.55 km，流域面积7 884 km2，占赣江流域面积的9.47%，是赣江下游西岸的一条重要支流，也是流经高安的第一大河流。其流域水系图见图1。

图1 锦江流域水系图

锦江干流自西向东蜿蜒流过高安市城区中部，城区段河长约13 km，宽约150～300 m，河床底高程20～24.5 m，较河岸低8.0～12.0 m，河道纵坡约0.6～2.0/10 000。

2.1 水文基本资料

高安市属亚热带湿润气候区，四季分明，气候温和，雨量充沛，光照充足且无霜期长。多年平均气温在17.5～17.9 ℃，极端最高气温40.4 ℃，出现在七八月份，极端最低气温-13.1 ℃，出现在一二月份，多年平均相对湿度83%，多年平均蒸发量965.1 mm左右，且各年变化不大，七八月份蒸发旺盛，各年最大月蒸发量均在7月份，可达240 mm。

全市雨量较为充沛，多年平均雨量1 672.4 mm，最大年降雨量2 427.1 mm，最小年降雨量1 123 mm，雨量空间分布呈现出北多南少、山区多于丘陵。降雨年内分配不均匀，主要集中在4-6月，约占全年降雨量的45.9%。本流域的径流主要来自降雨，径流的年际变化及年内分配极不均匀，坝址多年平均流量为181.1 m3/s，多年平均径流量57.1 亿m3，多年平均径流深908 mm。

高安水文站：位于高安市城区高安大桥上游200 m处，地理位置为:东经115°22″，北纬28°25″，控制集雨面积6 215 km2，该站实测断面稳定，河段顺直。该站于1949年10月由江西省人民政府水利局设立，有1961-1964年、1991-2016年历年实测流量资料。

2.2 参数确定

高安水文站有实测流量资料1961-1964年、1991-2016年，通过其邻近水文站贾村站实测流量系列插补延展得到高安站1953-2016年流量资料。将高安站1913年调查最大流量作特大值处理，采用PⅢ曲线适线，得到100年一遇、50年一遇以及20年一遇的洪峰流量分别为5 238、4 965及4 500 m3/s，根据高安站水位流量关系曲线查得各个设计标准相应的水位。选取高安站2010年6月17日至6月20日的一场洪水，作为典型洪水，按照洪峰流量同倍比放大法对典型洪水过程进行放大，得到锦江上游入口100年一遇、50年一遇以及20年一遇的流量过程线。根据工程提供的筠洲大桥下游1 522 m处断面为下游控制断面，利用曼宁公式计算断面各个水位对应流量，并形成下游控制断面水位流量关系曲线。

由《高安市五河治里防洪工程可研报告》中确定的锦江河道糙率取值范围0.026～0.035。根据历史相关资料和经验，各河段糙率参数选取0.033。根据锦江常水位取断面迭代的初始水深为1.84 m。计算时间步长根据模型的稳定性进行反复调试，最终取值0.16 h。

代表性分析：绘制高安站流量模比系数差积曲线，其流量资料的累积值首尾基本趋近于1，可认为高安站1953-2016年系列流量资料具有较好的代表性。

2.2.1 MIKE

计算时间步长为0.16 h。

边界条件：上游入口给定100年一遇、50年一遇以及20年一遇的流量时间序列文件和下游河口位置的水位流量关系曲线。

河道综合糙率：0.033。

断面迭代的初始水深为1.84 m。

2.2.2 HEC-RAS

计算时间步长为0.16 h，输出时间步长为1 h。

边界条件：上游入口给定100年一遇、50年一遇以及20年一遇的洪水流量过程，以及各个设计标准的初始水位别为33.82、33.48、32.79 m。

河道综合糙率：0.033。

3 计算成果

3.1 水位计算成果

将为了推求高安城区锦江的水面线，将对河道进行概化，利用MIKE11一维水动力模型和HEC-RAS模型对锦江各个设计标准的洪水情况进行模拟，并计算得出其水面线。如表1所示，MIKE11模型和HEC-RAS计算出的河道水面线图如图2所示。

表1 设计洪水过程线表 m

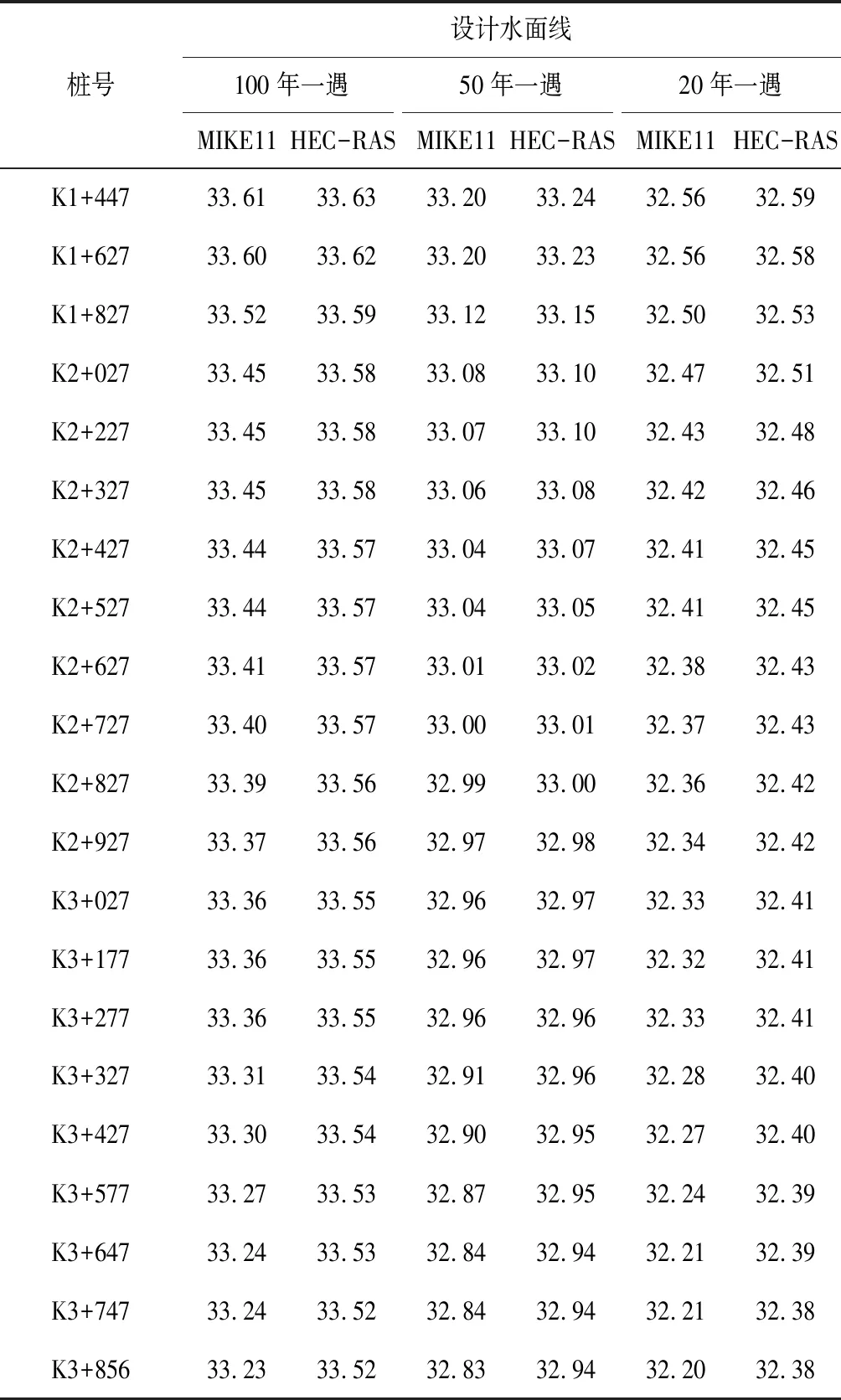
续表1 设计洪水过程线表 m

3.2 流速计算成果

由于还需获取河道流速数据进行对比分析，需用MIKE21进行建模。

模型运行结束后，将不同断面处的流速成果进行提取。HEC-RAS的计算结果可在流速列表中直接读取。

根据流速成果列表，可获取不同里程的流速，由于数据量较大，因此读取以下3个桩号的数据，如表2所示。

由表2可知，与HEC-RAS模型计算的流速相比，MIKE21模型的流速结果稍大一些。

4 成果对比分析

将两个模型的计算所得水位与《高安城防规划报告》中锦江流域旁的水文站高安站实测水位进行对比，报告中记录了本河段10个桩号的实测水位值，经计算得出50年一遇和20年一遇水位的纳什效率系数NSE和平均绝对误差e，如表3所示。

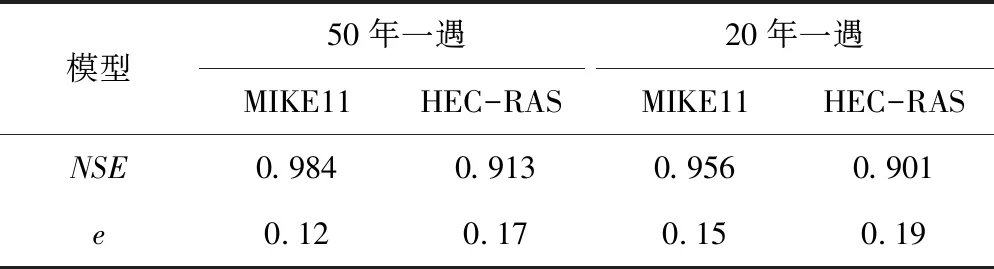
表3 水位精度评价表

由表3可知，MIKE11 模型计算的水位纳什效率系数相对较高，因此用MIKE11计算水面线的误差更小，结果更加可靠。HEC-RAS 模型与MIKE11 模型在不同设计标准的洪水水位的计算结果相差不大，但前者的计算洪水位普遍略高于后者的计算洪水位。锦江设计标准为50年一遇和20年一遇的河道水面线，如图3所示。

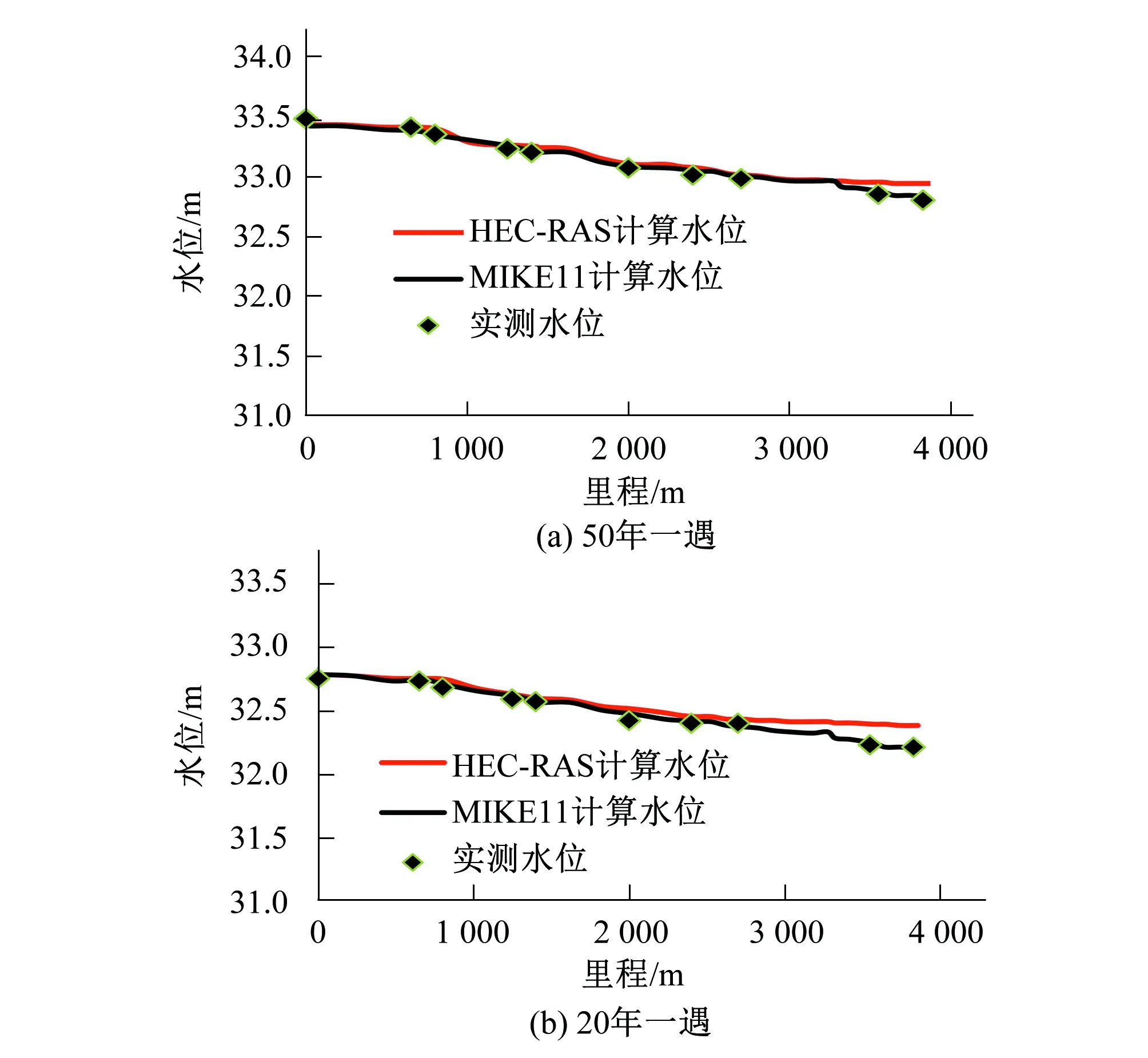
图3 HEC-RAS 和MIKE11 计算水位对比图

对于研究区域锦江河道而言，两个模型计算的水位和流速成果大体相同，模拟计算的结果是MIKE11模型计算的水位具有更高的准确度； MIKE21模型计算的流速大于HEC-RAS模型计算的流速。考虑到两个模型的原理及方程建立的过程和模型操作时参数设置的影响，认为上述现象产生的原因大抵有下面三项。

4.1 水力半径

两种水面线计算模型根据不同的河道类型、水体流态以及断面形态来采用不同的水力半径，一般根据经验和水力学特性选择水力半径类型：深窄型河道，阻力半径计算的特性流量往往偏大，适合用水力半径；对于有较大面积滩地的河道，一般采用阻力半径。

阻力半径：

(A为过水断面面积)

(5)

水力半径：

(6)

对于锦江研究流域，MIKE11模型选用式(5)计算的阻力半径，HEC-RAS模型则是采用水力半径。由于水力半径计算方式的不同，导致两个模型水面线推求结果有一定的差异。

4.2 控制方程

因为二者的模型原理与控制方程不同，所以迭代收敛条件以及求解方法不同，MIKE11模型运用六点Abbott-Ionescu隐式差分格式求解，而HEC-RAS模型是采用Newton-Raphson 迭代法计算水面线。6点 Abbott-Ionescu隐式格式的计算网格点布置方式如图4所示。HEC-RAS模型是基于四点隐式差分格式进行离散的。

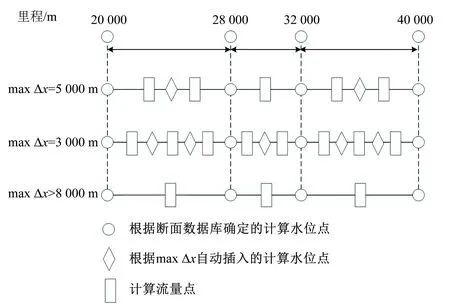
图4 6点 Abbott格式的计算网格点布置图

4.3 参数敏感性

使用MIKE模型和HEC-RAS模型推求锦江河道水面线的过程中，涉及很多参数，经过分析发现河道糙率和初始水深可能是较为重要的。参数敏感性分析是指影响河道水面线的各个参数发生变化时，对河道水位影响的大小，参数变幅相同时，河道水位变化越大的，参数越敏感，河道水位变化越小的，参数越不敏感。下面以100年一遇的设计洪水为例，研究河道糙率和初始水深在以上两个模型中的敏感性。参数的变幅依次是-50%、-20%、0、+20%和+50%，如表4所示。

采用MIKE模型和HEC-RAS模型对改变后参数进行的锦江河道水面线计算，每次按照变幅改变其中1个参数大小，其余参数保持不变，依次计算这两个参数不同变幅时的所有桩号的水位，并求出每个桩号水位的变幅大小，取平均值，如表5与表6所示。

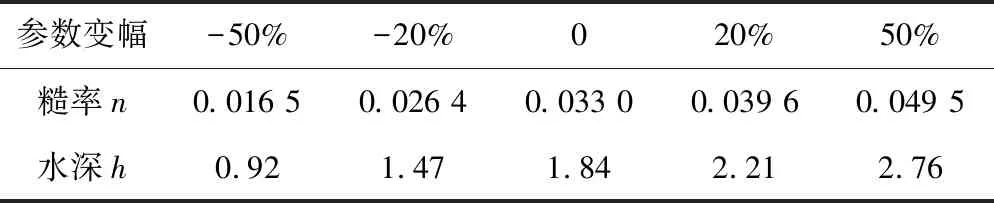
表4 模型参数表

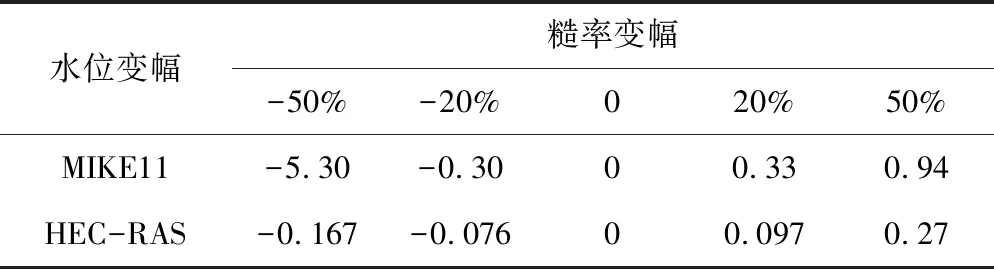
表5 水位对糙率的敏感性分析表 %

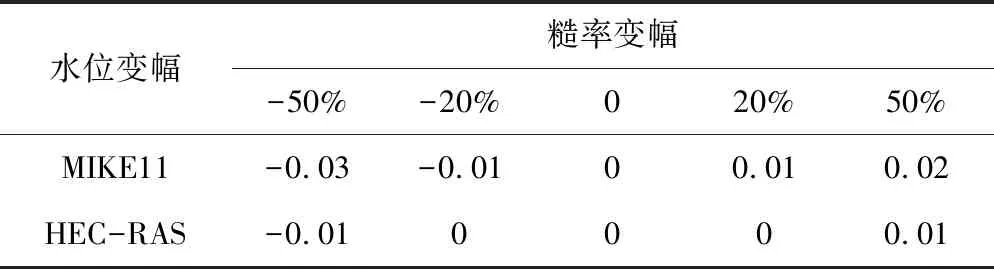
表6 水位对初始水深的敏感性分析表 %

从表5和表6可以看出，在河道糙率变幅相同时，MIKE模型的水位变幅比HEC-RAS模型的要大得多。因此，MIKE模型的水位对糙率的敏感性比HEC-RAS模型更强。但是这两个模型推求的水面线对初始水深皆不敏感，初始水深的变化引起最后水位的变化很小，水位基本保持不变。经过反复试验，水深变幅足够大时，对水面线推求的结果影响仍不是很大。

5 结 语

(1)在河道的水文条件一致的前提下，MIKE11模型推算的水面线精确度更高，其水位结果也略高于HEC-RAS模型。而两种模型在流速的计算成果中，MIKE21模型计算的流速稍大。

(2)两者相比，MIKE模型的水位对糙率的敏感性更强。但是这两个模型推求的水面线对初始水深均不敏感。

(3)在选择合适的模型进行研究流域河道水面线计算时，可考虑以下几种情况。当河床糙率在河段的变化较大时，建议选用MIKE11 模型进行水面线推算；若河床冲刷速度对水利枢纽的建设影响较大，可使用HEC-RAS模型进行计算。对于工程项目的重点规划河道，应该结合河流流态实际情况，可先后分别使用HEC-RAS和MIKE模型进行研究流域河道水面线计算，以工程偏安全等角度进行模型的选择。

MIKE模型与HEC-RAS模型的水动力学模型算法基本已成熟，但均是解决的水动力过程，没有反应水文水动力耦合过程。这两个模型普遍存在着“水土不服”的问题，尤其是解决实时决策问题方面。