基于函数主成分的函数型数据分类研究

吴 菲，陈迪荣



基于函数主成分的函数型数据分类研究

吴 菲，陈迪荣*

（武汉纺织大学 数学与计算机学院，湖北 武汉 430200）

不同属性特征可以反映出数据不同的内在信息，越多的差异性特征对机器识别就更有利，但是越多的特征数目引起数据更高复杂度。针对函数型数据最主要的函数性和导数性这两大特征，本文提出对函数型数据函数特征、一阶导数特征和二阶导数特征的组合集成方法，然后引入函数型主成分分析的方法解决数据的复杂性问题，最后通过函数型主成分距离度量方式，采用k近邻（knn）分类以达到分类的效果。实验分析表明了函数型主成分分析方法与混合多特征组合距离的结合，在函数型数据分类中的有效性。

函数型数据；函数型主成分分析；特征组合；距离度量；knn

1 引言

通过数据分析进行学习是机器学习的重要方式，因此，数据的组织和分析方法对机器学习有重要的影响。随着“互联网+”模式的兴起，“大数据时代”已经来临，互联网将世界紧密的联系在一起，使得收集的样本数据更加密集和连续，甚至呈现出某种函数型规律。在数据空间中呈现了某种非常复杂函数关系的数据，称为函数型数据( 简称 FDA)。函数型数据最初由加拿大统计学家 Ramsay于1982年发表的论文《When the Data are Functions》[1]引入。1991年，Ramsay与Dalzell结合统计学、拓扑学和泛函分析的思想，在论文《Some Tools for Functional Data Analysis》中正式提出了函数型数据分析（Funtional data analysis,FDA）的概念和分析处理的方法[2]。2005年，Ramsay和Silverman撰写了《Functional Data Analysis，FDA》[3]一书，针对函数型数据改进了传统统计分析方法，提出对应的函数线性回归分析（FLR）、函数型主成分分析（FPCA）、函数型相关分析（FCCA）等方法。此后，函数型数据分析开始受到更广泛的关注并掀起了在各邻域的研究热潮，应用成果涉及医学诊断[4, 5]、金融工程[6, 7]、电子商务[8, 9]等领域。

函数型数据分析思想就是将观测数据拟合成光滑曲线进行处理，相较于传统的数据分析，观测数据被赋予了动态属性，以便挖掘出更多函数型数据内在规律和隐藏特征。实际上，光滑性一般指估计曲线的一阶或更高阶导数，是函数型数据分析框架中最为显著的重要特征之一。较之静态的情况，借鉴多元统计提出的FPCA[10-15]不仅很好地解决了高数据密度情况下的降维问题，还能显示出结果随时间而改变的动态特征。

分类识别中，每一种特征都是数据内在属性的反映，不同属性特征的分类识别结果不同，而且结果之间互补性很强[16]。因此，本文对具有函数特征的离散观测数据，首先利用B样条基函数的非参数平滑技术[17, 18]拟合成函数表示；再进一步集成函数曲线特征及其导数特征进行进行函数型主成分分析；最后，对分析出的综合特征采用最简单的k近邻值（Knn）[19]分类方法进行分类识别。

2 函数型数据分析方法

2.1 数据预处理——纵向标准化

受函数型数据的异常值[21]样例间特征未对齐等因素的影响，函数主成分对函数型数据的表示能力退化，使函数型数据的模式识别能力变弱。函数型数据主成分分析前，若类内函数样例未进行特征对齐或各个函数样例的值域差异较大时，可以先对函数型数据进行纵向标准化变换，然后对变换后的数据进行函数主成分分析。

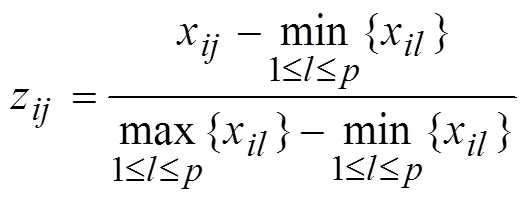
上式称为纵向标准化变换。值得注意的是，上述变换并不改变函数型数据的整体趋势，且该变换使得每个函数型数据的值域均为区间[0，1]。

2.2 函数化表示

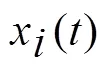
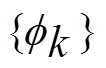
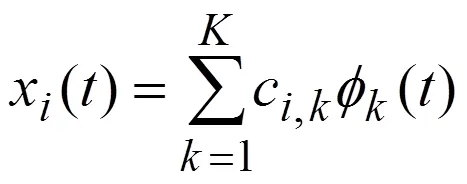
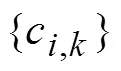
2.3 函数型主成分分析

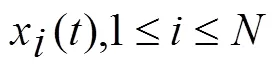
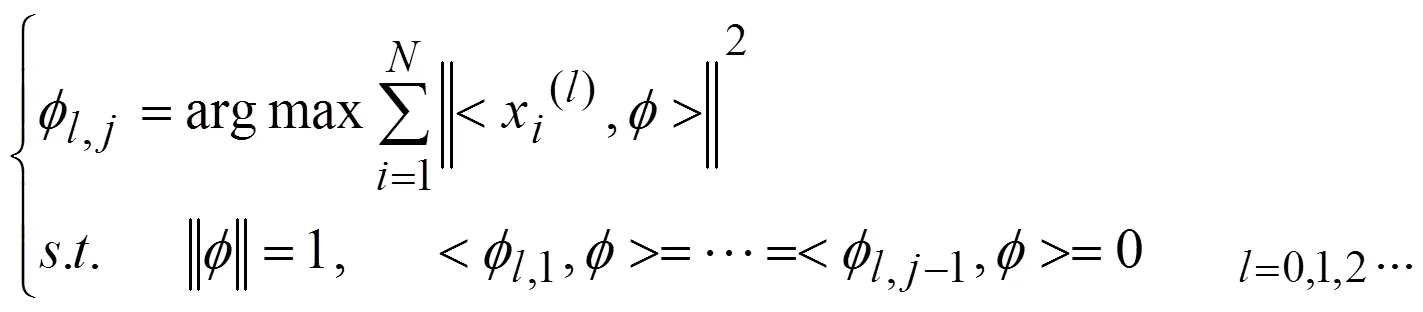
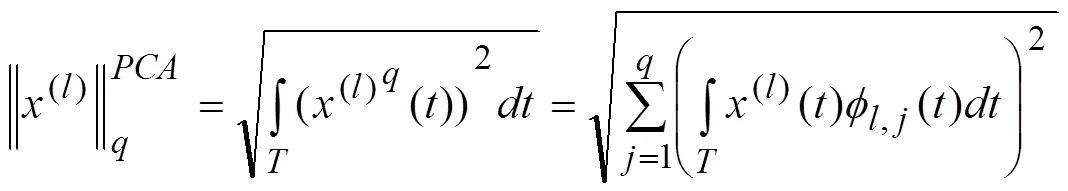
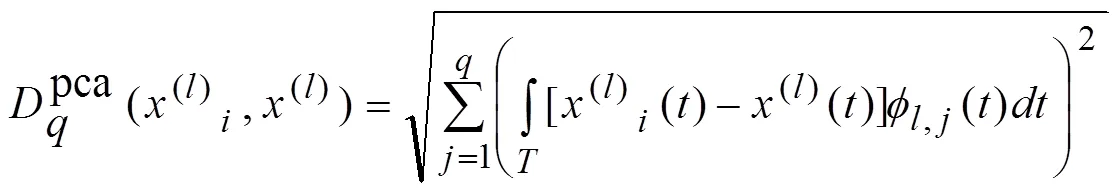
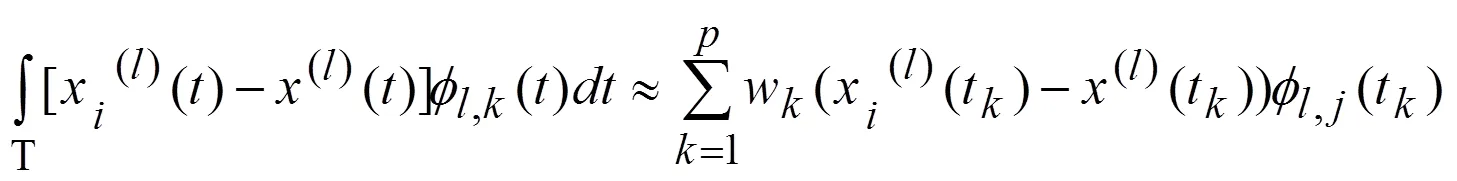
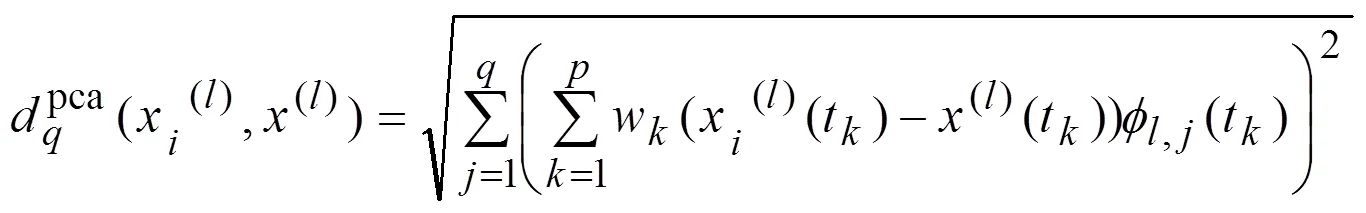
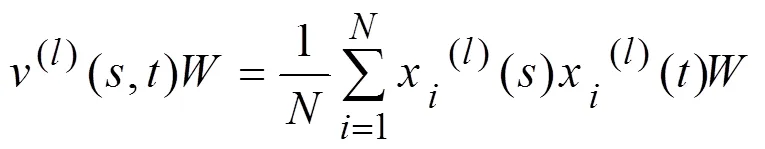
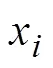
或者写成：

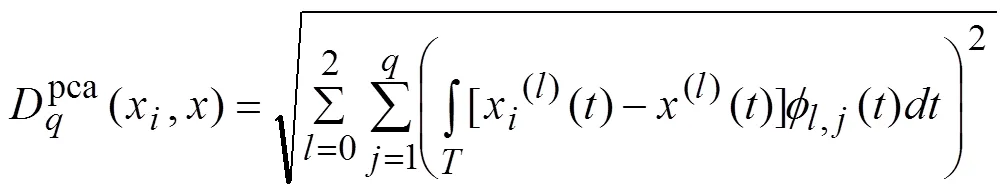
图1 本文研究方法的简要流程图

3 数据实验及结果分析

为了验证本文方法在函数型数据分类中的有效性，本文在两个数据集上进行了实验，其中Tecator数据集来源于UCI数据库中的标准数据集[23]，另外青光眼数据集由北京同仁医院眼科学协会提供。

3.1 Tecator数据实验分析

Tecator数据集主要是对碎肉样品的脂肪含量进行研究（数据来源：http://lib.stat.cmu.edu/datasets/ tecator）。每个样本对(x_i, y_i)中，x_i是第i个样品的吸光率（波长范围是850~1050nm），y _i是脂肪含量。把脂肪含量超过20%的标为负类（Bad），把脂肪含量低于20%的标为正类（Good）。该数据集由215个碎肉样品构成，每个碎肉样品包括100个不同波长的近红外光的吸收度值，其中，正类样本138个，负类样本77个。根据训练样本构造算法，使得利用测试样本的吸光率x，可以预测其脂肪含量是否超过20%。

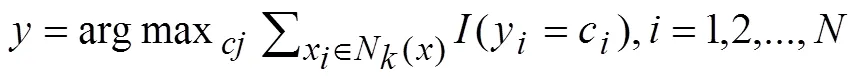
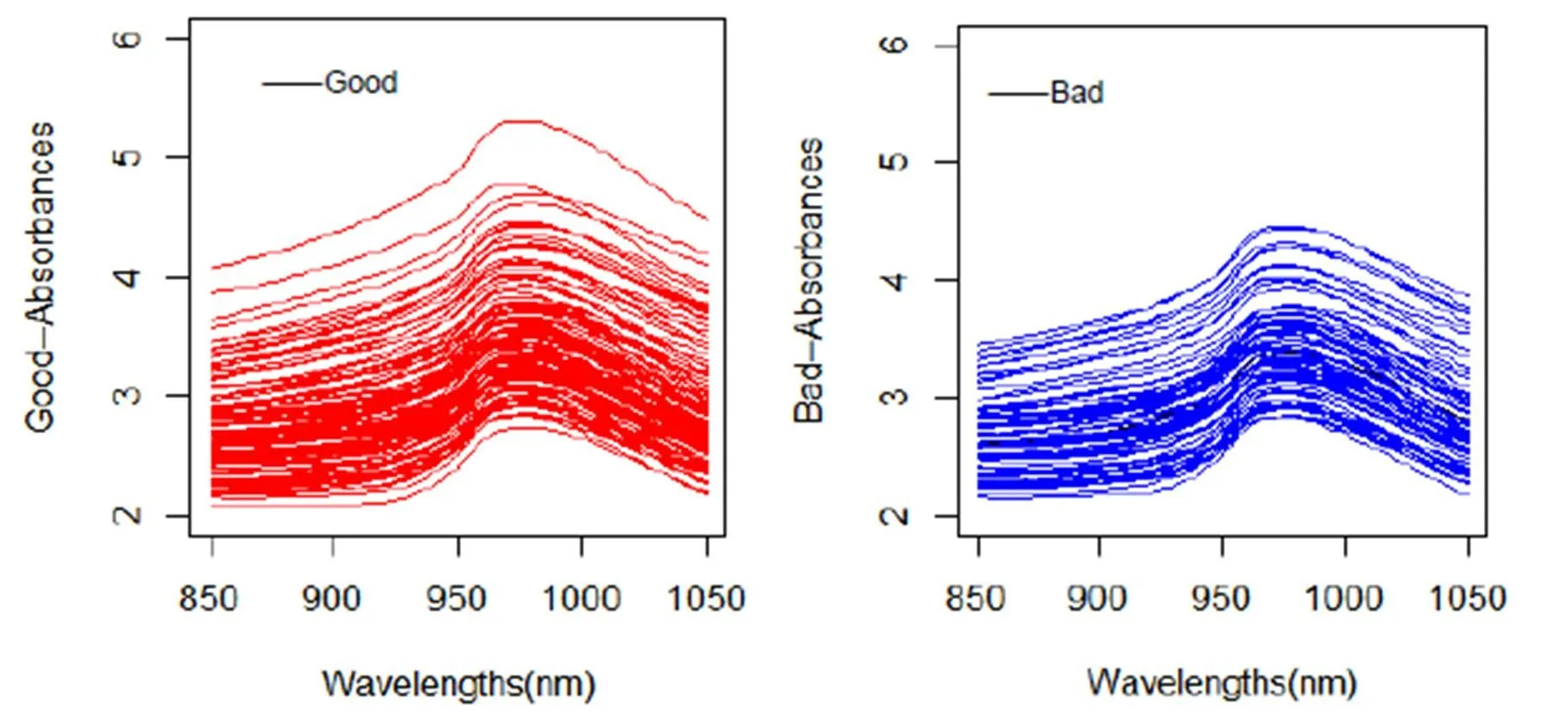
图2 Tecator数据集光谱吸收度的函数曲线

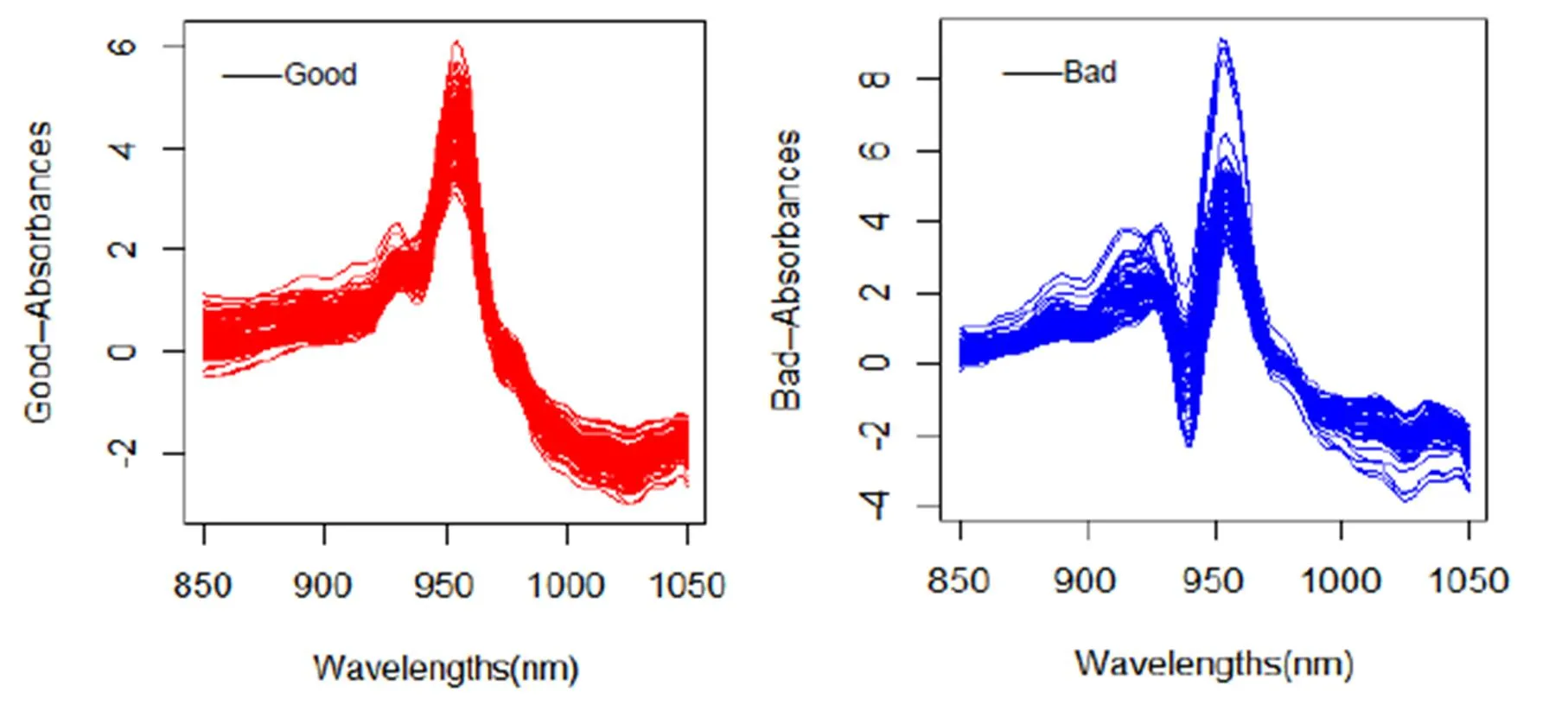
图3 Tecator数据集光谱吸收度的一阶导数

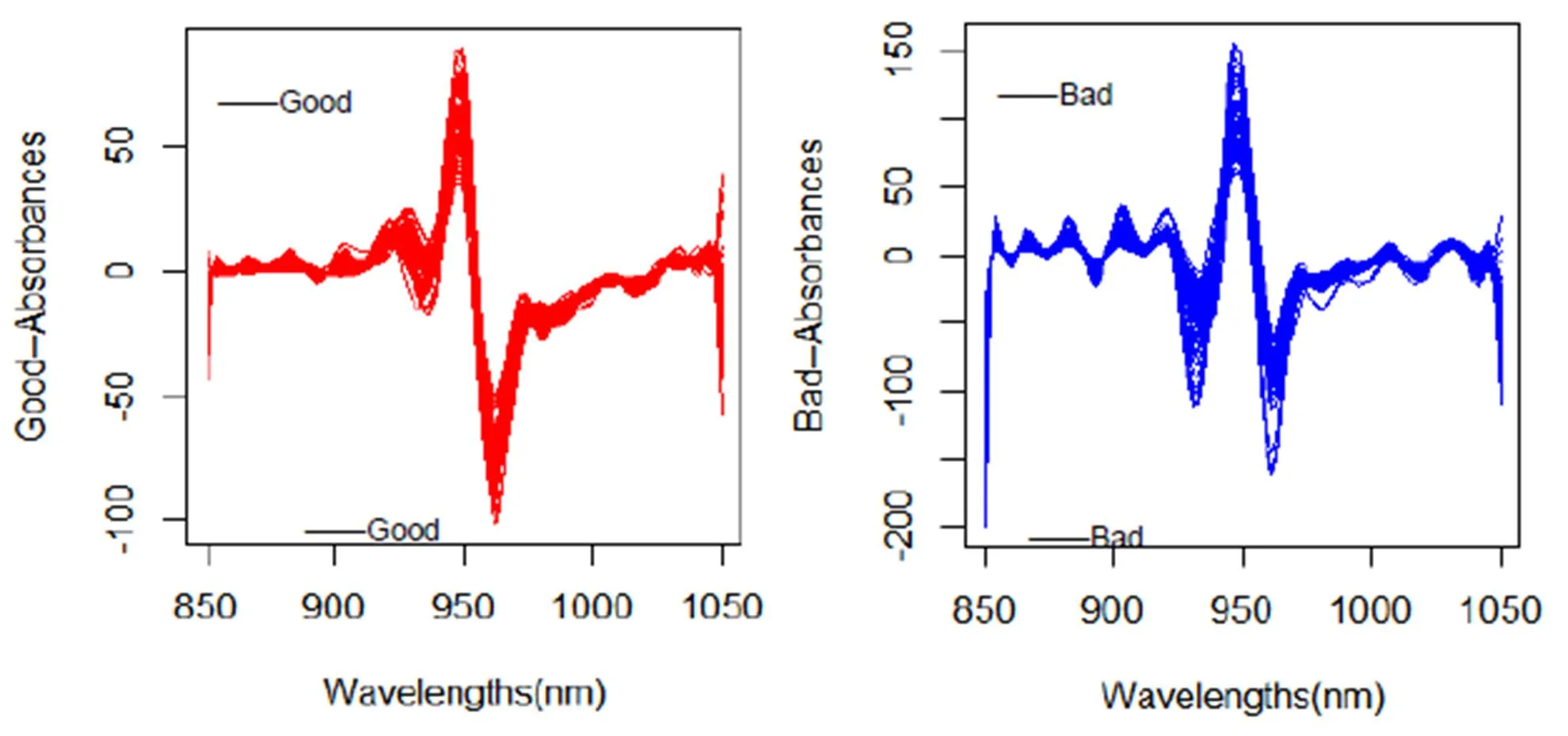
图4 Tecator数据集光谱吸收度的二阶导数

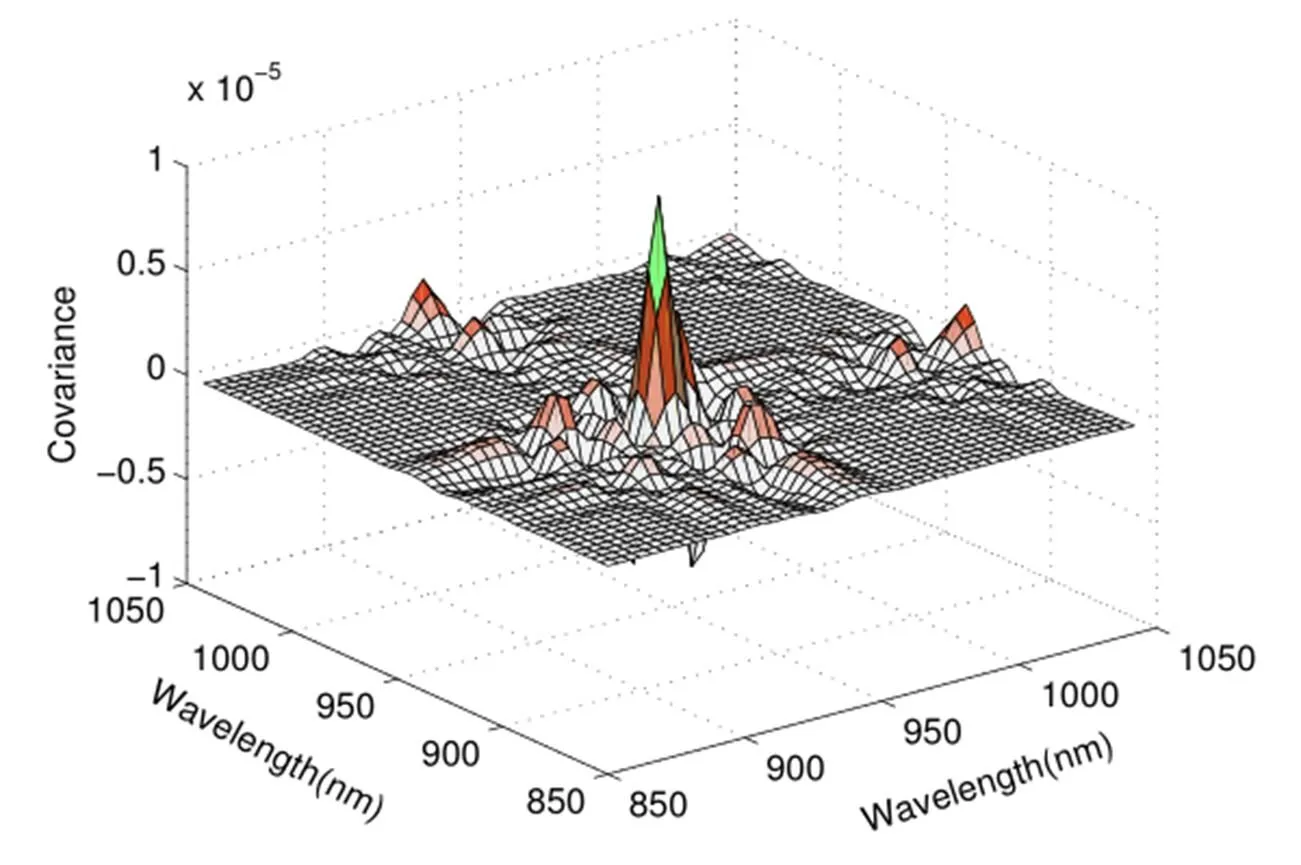
图5 Tecator数据集的样本协方差曲面

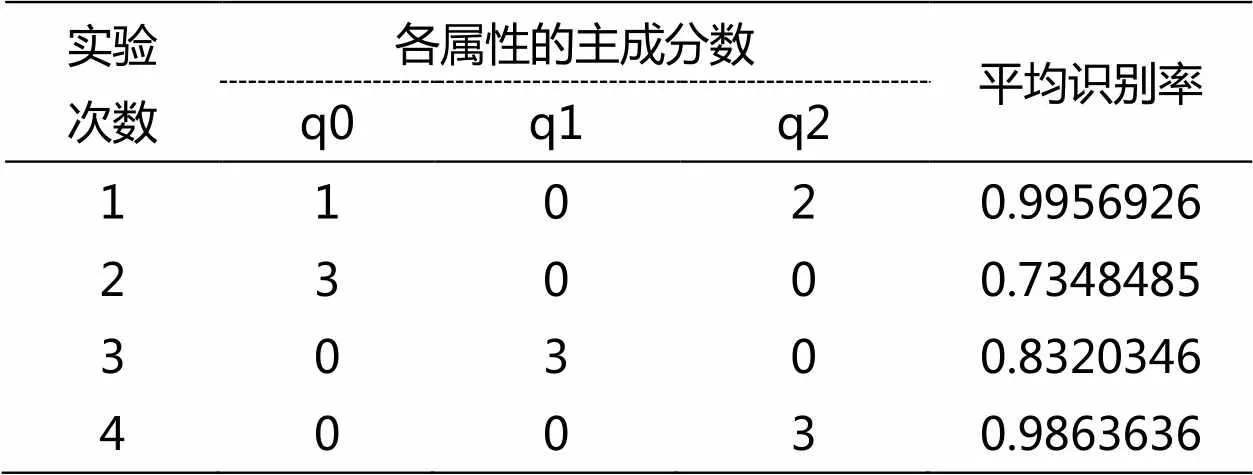
表1 Tecator数据集函数主成分组合距离分类识别率

观察样本协方差曲面（图5），对角线表面的高度变化很大，特别是[925,950]这段波长范围内，各点的方差较大。两类数据的函数曲线图（图2）以及导数曲线图（图3、图4）也都体现这一点，特别是二阶导数曲线，它基本与整个协方差曲面的特征保持整体上较高的一致性。此次实验，当函数主成分数为1，一阶导数主成分数为0，二阶导数主成分数为2时，验证集的平均识别率最高（0.9766234）。测试集数据实验结果如表1所示，其中（q0：函数的主成分数，q1：一阶导数主成分数，q2：二阶导数主成分数）。

实验结果显示，此次试验通过交叉验证获得的最优参数在测试集上也表现出很好的效果，平均识别率高达0.9956926，基本接近于1了，比其他组合结果和单一结果都要优。与协方差曲面（图5）表现结果一样，二阶导数更能反映出数据的差异特征，单一二阶导数的情况比其他单一情况好很多，只比最优组合结果差一点点；单一一阶导数距离识别效果比单一函数距离识别率高一点，但是这两个单一距离的识别效果与其他相比还是不够的。文献[25]中利用稳健主成分分析方法与支持向量机分类器对Tecator数据脂肪含量进行分类的准确率最优结果为0.9818，本文的组合结果的分类精度仍具有一定优势。

3.2 青光眼数据实验分析

青光眼是一种以视神经乳头(Opticnerve head，ONH)结构改变为特征的进展性视神经病变，世界卫生组织将其列为全球第二大致盲眼病。目前，计算机辅助诊断是青光眼诊断研究的重点。2002年，国际知名青光眼专家W．Einreb[24]及其合作者提出了应用机器学习辅助青光眼诊断的方法。他们应用主成分分析(PCA)方法对视野检测结果进行数据降维，进而应用支持向量机(SVM)等机器学习算法做青光眼数据分类问题，取得比传统统计方法更优的预测性能。这一成果引起人们对机器学习用于青光眼诊断的重视。

对我们提出算法进行测试的眼底照OCT图像数据，来源于北京同仁医院眼科学协会这些样本包含了346例眼底照组成的数据集，每个样例有360个特征数据，其中正常眼258个样例，青光眼88例。本实验利用函数型数据方法，将360维的杯盘半径比向量拟合为杯盘比曲线函数，利用曲线函数的一阶导数距离作为距离度量，并分别画出了前50个正常眼和青光眼的函数曲线，一阶导数曲线和二阶导数曲线分别如图6、图7、图8所示：

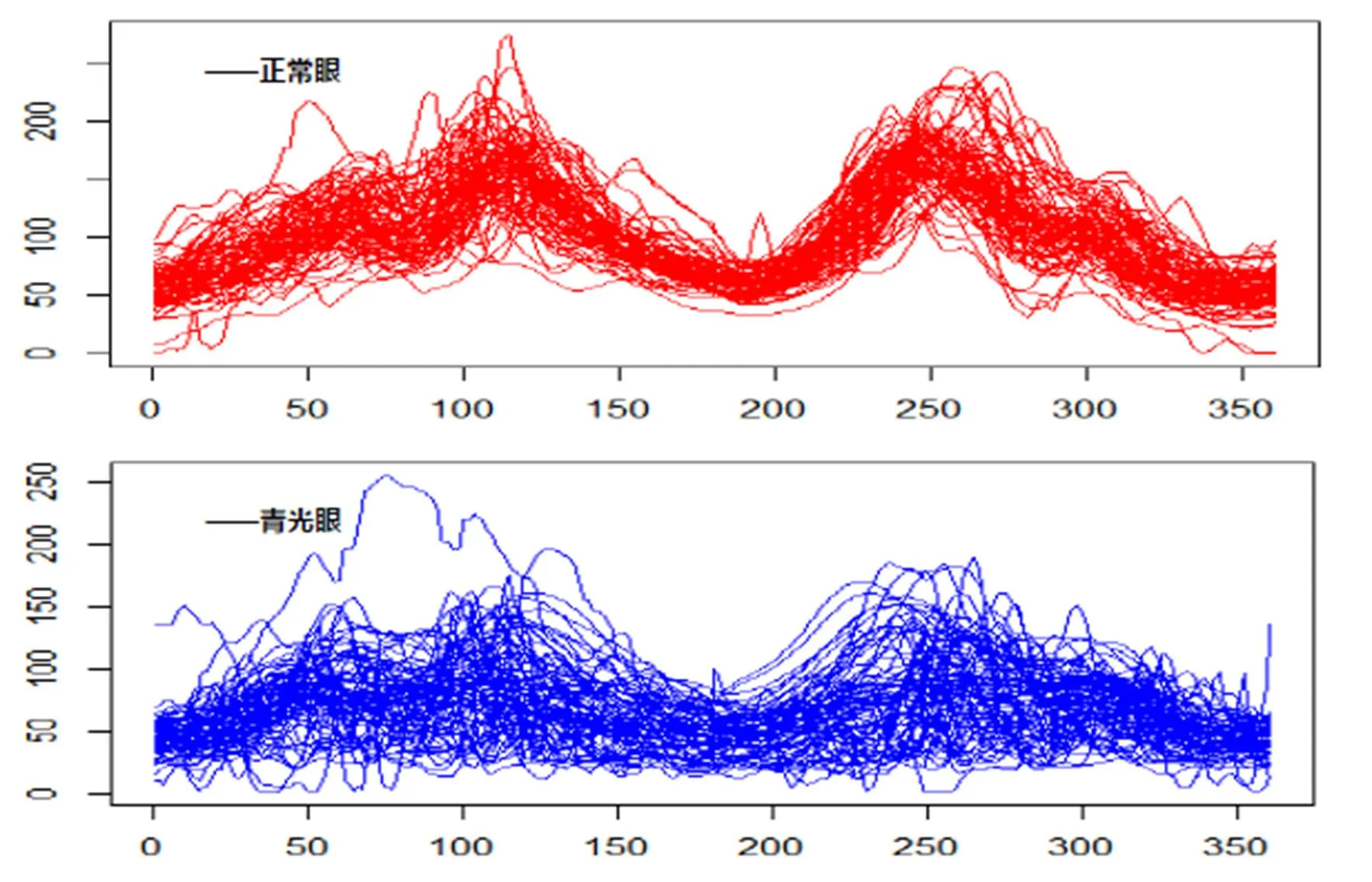
图6 青光眼数据的函数曲线

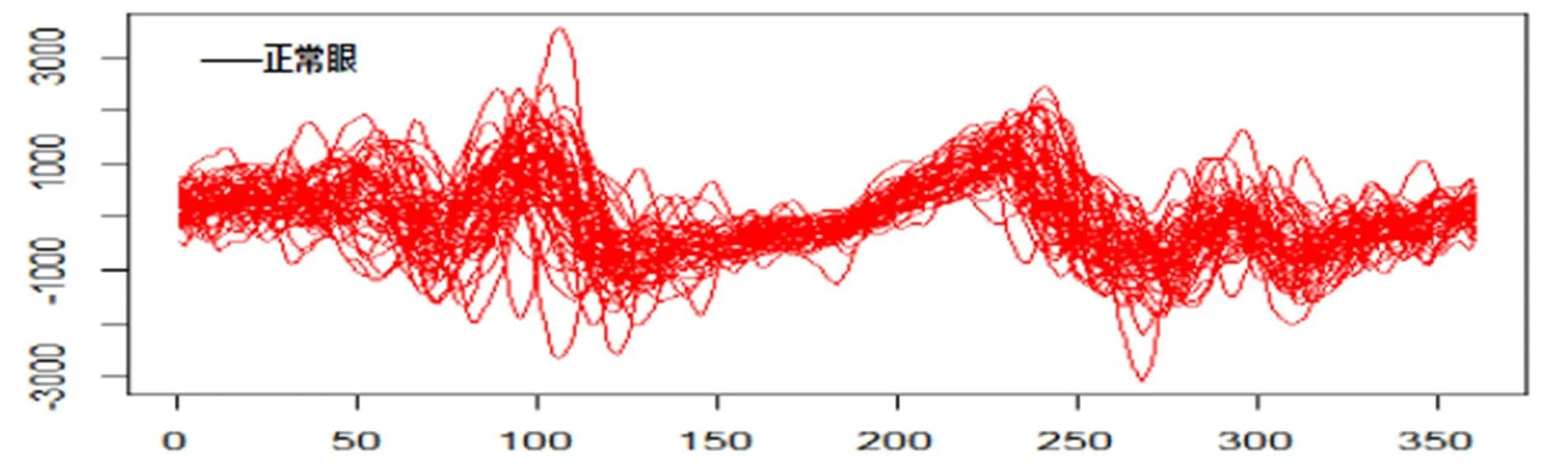
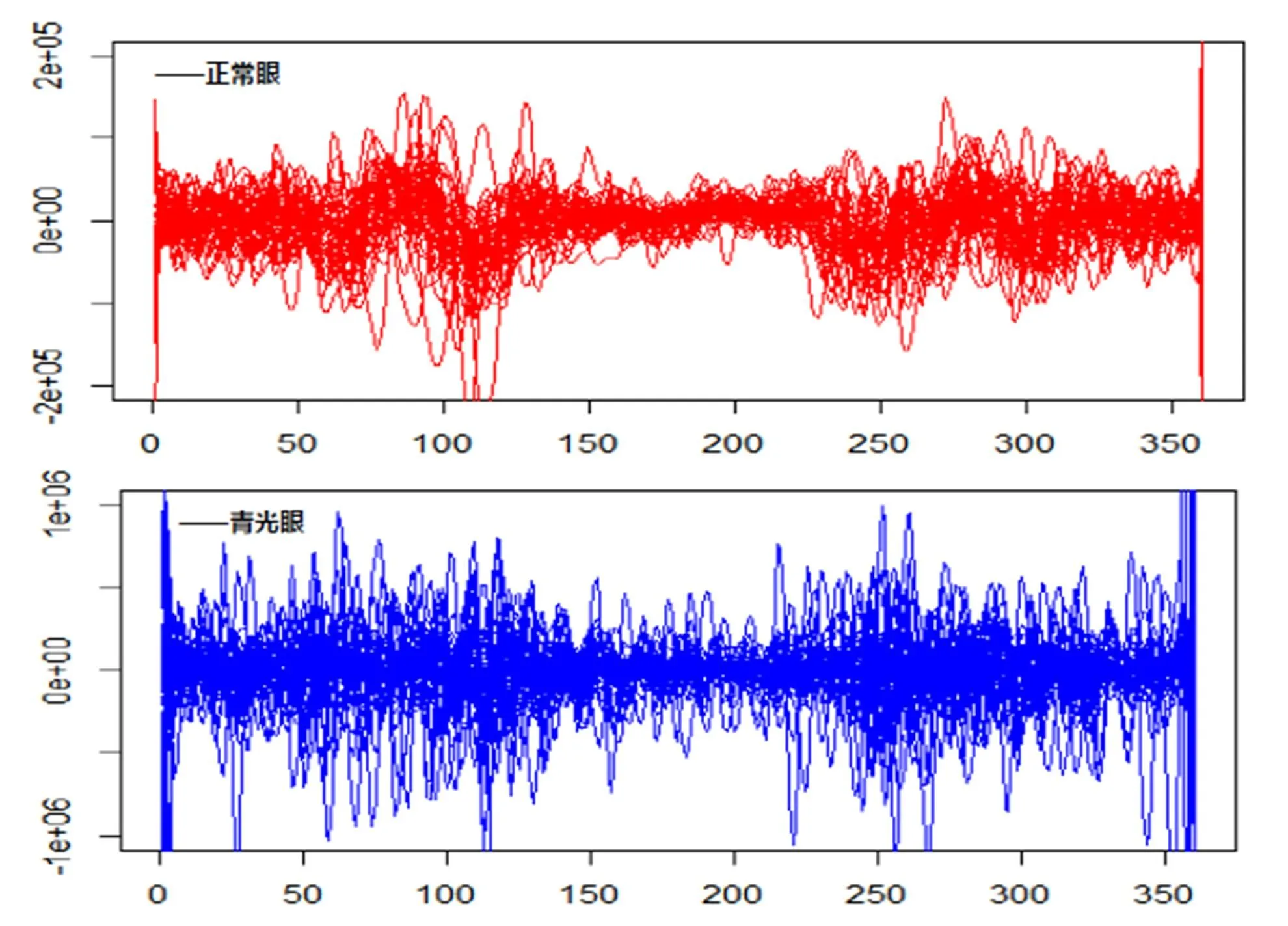
图8 青光眼数据的二阶导数曲线

青光眼数据实验方式与Tecator数据集的实验方式一样，也是将样本随机分成10份，分别取1份作为测试集和验证集，剩下的8份作为训练集，利用验证集通过交叉验证的方法获取最佳的平均识别率对应参数取值，再将此参数应用到测试集中，以10次平均识别率作为最终的识别率。青光眼数据验证集的平均识别率最高为0.9766234，此时函数主成分数为4，一阶导数主成分为数1，二阶导数主成分数为0。测试集数据实验结果如表2所示：

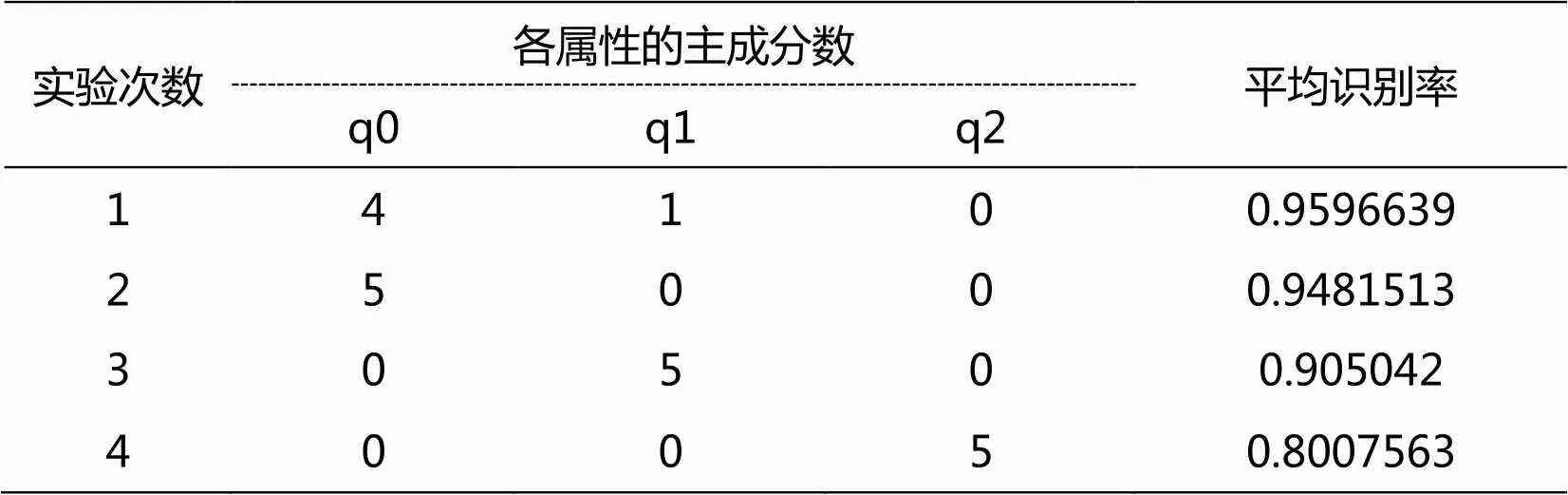
表2 青光眼数据集函数主成分组合距离分类识别率

实验结果可以看到，此次青光眼试验通过交叉验证获得的最优参数在测试集上也取得了较为理想的结果，平均识别率高达0.9596639，比其他组合情况和单一情况都要优。从青光眼单一特征距离分类效果来看，函数距离效果最好，一阶导数次之，二阶导数最差，这个跟上面光谱数据的数据属性相反，并不是越高阶导数，特征越明显。从图6-图8的曲线图展现了二阶导数曲线的弱差异性，两类样本的二阶导数曲线基本相差无几。青光眼的原始函数特征在这三个属性特征中占主导地位。2015年文献[26]通过神经网络的分割方法对117名青光眼患者和123名正常眼患者进行分类实验，由于分割方式造成分类结果的不一样，文献中Specificity最高为95.12%时对应的Sensitivity为58.12%；当Sensitivity最高为77.78%时对应的Specificity为80.49%；虽然该文章通过Sensitivity和Sensitivity分别计算青光眼和正常眼的分类准确率，但总体而言，本文的综合准确率还是更加稳定。

4 结语

本文主要介绍了函数型主成分分析方法在函数型数据分类中的作用，并在以往距离度量的基础上提出了组合多种特征的函数型主成分距离度量方法，巧妙地利用不同特征的主成分个数的选取差异性来体现不同特征的权重意义，避免加入新的权重参数，增加实验的复杂性。即使通过最简单的knn分类器，也能达到一个较为理想的效果，总体来说是验证了此方法的有效性。一般来说，函数特征或者导数特征都是数据本身的信息表现，都有其存在的价值，只是针对不同数据实例，最主要差异性特征属性会不一样，甚至有时候某个主导特征非常明显，单一结果会比组合结果好也是有可能的。并不是所有特征属性都是正向加强的作用，有时候组合叠加后也会出现负向抑制作用，这需要对具体问题进行具体分析。

作者对北京化工大学徐永利副教授表示衷心感谢，他为本文提出了不少建设性建议，并提供了青光眼数据。

[1] Ramsay，J O．When the data are functions[J]．Psychometrika，1982，47：379-396．

[2] Ramsay，J O，Delzall，C J．Some tools for functional data analysis (with discussion)[J]．Journal pf the Roval Statistical Socieyv，B，1991，53：539-572．

[3] Ramsay J O，Silverman B W. Functional data analysis(Second ed.)[M]. New York：Springer. 2005．

[4] Hu Y，He X M，Tao J，et al．Modeling and prediction of children’s growth data via functional principal component analysis[J]．Science in China Series：Mathematics，2009，52(6)：1342-1350．

[5] 王劼，黄可飞，王惠文．一种函数型数据的聚类分析方法[J]．数理统计与管理，2009，28(5)：839-844．

[6] Müller H G，Sen R，Stadtmüller U．Functional data analysis forvolatility[J]．Journal of the Econometrics，2011，(165 )：233-245．

[7] 郭均鹏，孙钦堂，李汶华．Shibor市场中各期限利率波动模式分析—基于 FPCA方法[J]．系统工程，2012，30(12)：84-88．

[8] Jank W，Shmueli G，Zhang S．A flexible model for estimating pricedynamics in on-line auctions[J]．Journal of the Royal StatisticalSociety：Series C， 2007，59(5)：781-804．

[9] Zhang S，Wjank，etal．Real-Time Forecasting of Online Auctions via Functional K-Nearest Neighbors[J]．InternationalJournal of Forecasting，2010，(26)：666-638

[10]王洁丹，朱建平，付荣．函数型死亡率预测模型[J]．统计研究，2013，30(9)：87-93．

[11]Jiang C，Wang J L．Covariate adjusted functional principal components analysis for longitudinal data[J]．The Annals of Statistics，2010，38：1194-1226．

[12]Sun Y，Genton M G．Functional Boxplots[J]．Journal of Computational and Graphical Statistics，2011，20：316-334．

[13]Boente G，Salibian-Barrera M．S-estimators for funcitonal principal component analysis[J]．Journal of the American Statistical Association，2014 110(51)：1100-1111．

[14]Chiou J M，Li P L．Functional clustering and identifying substructures of longgitudinal data[J]．Journal of the Royal Statistical Scoiety：Series B，2007，69：679-699．

[15]Hall P， Müller H G，Wang J L．Properties of principal component methods for functional and longitudinal data analysis [J]．Annals of Statistics，2012，34(3)： 1493-1517．

[16]Ho T K，Hull J J，Sirhari S N．Decision Combination in Multiple Classfier Systems[J]．IEEE Transactions on Pattern Analysis and Machine Intelligence，1994，16(1)：66-75．

[17]Eubank R L．Nonparametric Regression and Spline Smoothing(2 ed)[M]．New York： MarcelDekker，Inc，1999．

[18]Fan J，Gijbels I．Local Polynomial Modelling and its Applications[M]．New York：CRC Press，1996．

[19]Nenad T，Krisztian Ba．Hubness-aware kNN classification of high-dimensional data in presence of label noise[J]．Neurocomputing， 2015，157：172．

[20]Jacques J，Preda C．Functional data clustering： a survey[J]．Ad-vances in Data Analysis and Classification，2014，8(3)：1-24．

[21]Shang H L．A survey of functional principal component analysis[J]．AStA Advances in Statistical Analysis，2014，98(2)：121-142．

[22]Castro，PE，Lawton WH，Sylvestre EA．Principal modes of variation for processes with continuous sample curves[J]．Technometrics，1997，28，329-337．

[23]UCI machine learning repository[EB/OL]．http：//archive.Ics.Uci.edu/ml/datasets/ Hill-valley，2014-03-17．

[24]Chan K，Lee T W，Sample P A，etal．Comparison of machine learning and traditionalclassifiers in glaucoma diagnosis [J]．IEEE transactions on bio-medical engineering，2002，49(9)：936-97474．

[25]孟银凤，梁吉业．函数型数据分类中的稳健主成分分析[J]．小型微型计算机系统，2016，37(7)：1499-1503．

[26]Larrosa J M，Polo V，Ferreras A，et al． Neural Network Analysis of Different Segmentation Strategies of Nerve Fiber Layer Assessment for Glaucoma Diagnosis[J]．Journal of Glaucoma，2014，24(9)．

Functional Data Classification based on Function Principal Component

WU Fei, CHEN Di-rong

(College of Mathematics and Computer,Wuhan Textile University, Wuhan Hubei 430200, China)

Different attribute characteristics reflect different intrinsic information of data. The more different features, the more favorable for machine recognition. On the other hand, more feature numbers cause the higher complexity of data. According to the two main features of functional data, that is functional and derivative property. This paper proposes a combined method of functional data with function, first and second derivative property.And then it introduces functional principal component analysis(FPCA) to treatthe complexity of the data. Finally k-nearest neighbor (knn) is used to achieve the classification by functional principal component distance metric. The experiment shows the effectiveness of combination of functional principal component analysis(FPCA) withmixed Multi-distance Metricsto functional data classification.

functional data; functional principal component analysis; mixed multi-distance metrics; k-nearest neighbor(knn)

陈迪荣（1961-），男，教授，博士生导师，研究方向：机器学习.

国家自然科学基金资助项目（11571267）.

TP391

A

2095－414X(2019)02－0048－09